拉脱速度对测量水表面张力系数影响的研究

崔钧晟,吴秀梅

(1.东南大学 物理学院,江苏 南京 211198;2.东南大学 吴健雄学院,江苏 南京 211198)

拉脱法研究水的表面张力系数是一种操作简单的实验方法,但实验发现,水表面张力系数的测量值常常会受到很多外在因素的干扰,比如实验中所用圆环的横截面积、圆环厚度、圆环水平程度以及实验温度等[1-7],使得测量值和真实值之间产生较大的偏差。除此之外,作者在实验中还发现,圆环的拉动速度对测量水表面张力系数同样存在着重要的影响,但现有的报道中很少见到相关研究。因此,本文将着重研究拉动圆环的速度,对测量水表面张力系数的影响。

1 实验原理

表面张力系数的拉脱实验原理,如图1所示[8]。圆环上端与力敏传感器相连,位置保持不变。调节金属杆上升降螺母,使其上端平台上盛液体(本实验的液体为水)的容器相对圆环位置下降,则容器中水面位置相对圆环位置下降,从而实现圆环与水面的拉脱。通过测定圆环与水面拉脱前后力的变化,用来描述圆环在拉动过程中受到的表面张力,从而可以计算出水的表面张力系数。

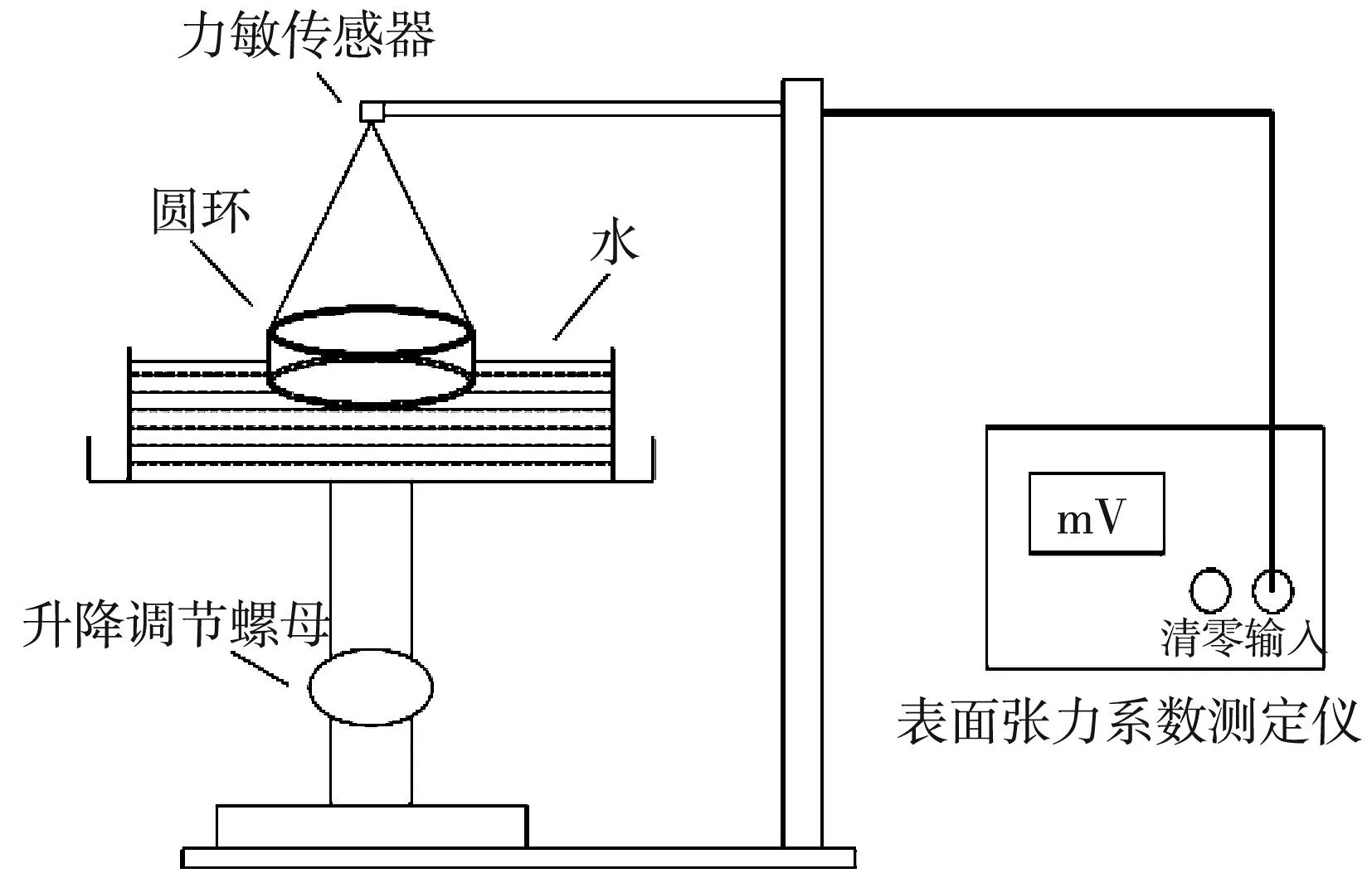
图1 拉脱法实验原理图

根据液体表面张力原理可以得出,在圆环没有拉脱的时候,圆环除受到重力之外,还受到水面对圆环的拉力。一般情况下,水面对圆环拉力的大小等于水的表面张力和浸润角的余弦值的乘积:

F=2πσ(r+R)cos(φ) ,

(1)

其中σ为表面张力系数;r与R分别为圆环的内径和外径;φ为浸润角(浸润角为水膜表面与圆环侧面的夹角)。由于在实验中,圆环将要拉脱的时候浸润角很小[9],所以可以近似认为cos(φ)=1,即水面对圆环拉力近似等于水的表面张力,即:

F=2πσ(r+R) 。

(2)

而在圆环和水面拉脱之后,由于没有了表面张力的作用,力敏传感器只受到圆环的重力作用。因此,圆环和水面拉脱前后力敏传感器受到的拉力的差值就可以用来近似表示圆环受到的表面张力的大小。通过公式:

σ=ΔF/2π(r+R) ,

(3)

可以计算出水的表面张力系数的大小。

2 实验数据与分析

2.1 力敏传感器灵敏度的测量

力敏传感器的原理是将受力大小转换为相对应的电压值。本实验前,将一个砝码盘挂在传感器上,并将力敏传感器示数调零。然后依次向砝码盘中加入质量为0.500 g的砝码,记录下每一次的示数,如表1所示。

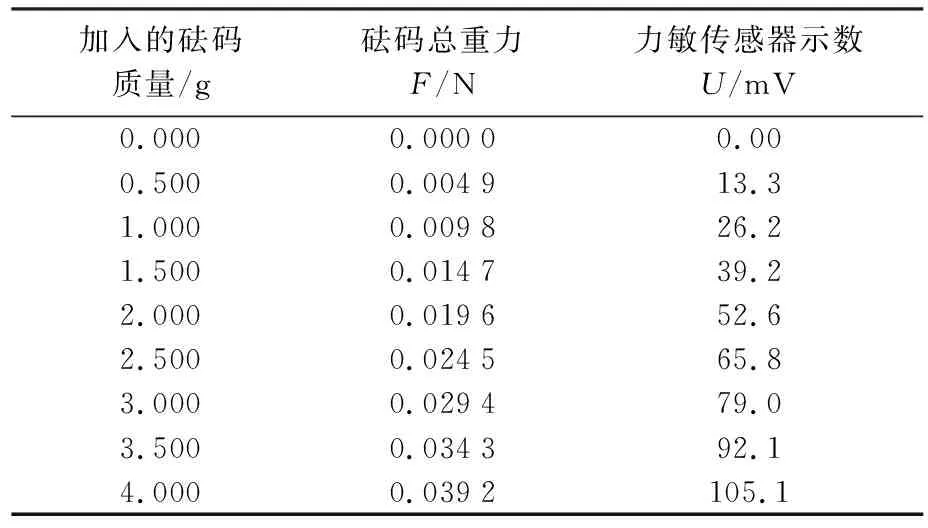
表1 力敏传感器敏感度的测量

根据力敏传感器的敏感度公式[10]:

k=ΔU/ΔF,

(4)

将表1的数据做线性拟合,如图2所示。得到拟合直线的斜率,即为力敏传感器的敏感度k=2 684 mV/N。(其中,ΔU为力敏传感器显示的电压的差值,单位为mV;ΔF为力敏传感器受到的外力的差值,单位为N)

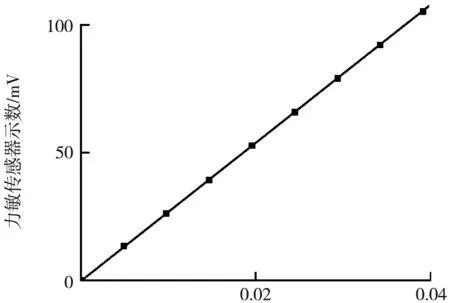
砝码总重力/N图2 砝码总重力与力敏传感器示数线性关系图

2.2 拉脱速度对表面张力系数测定的影响

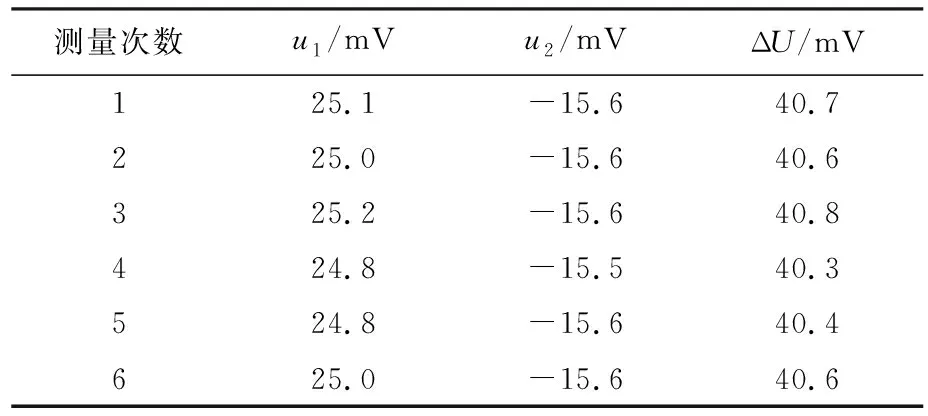
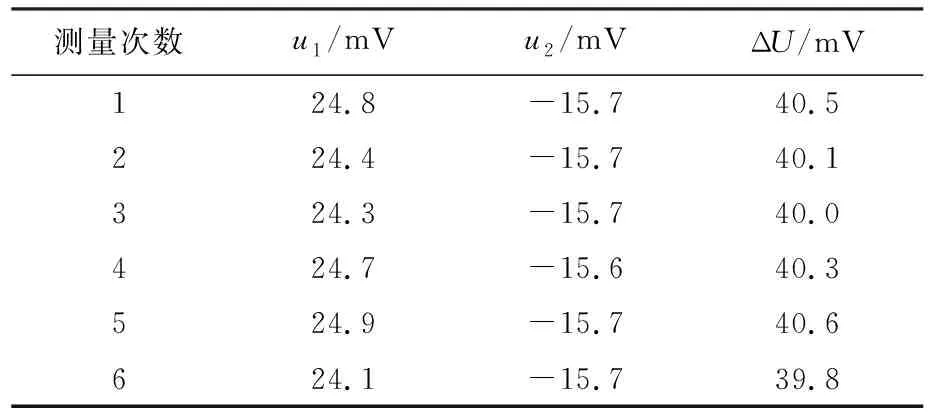
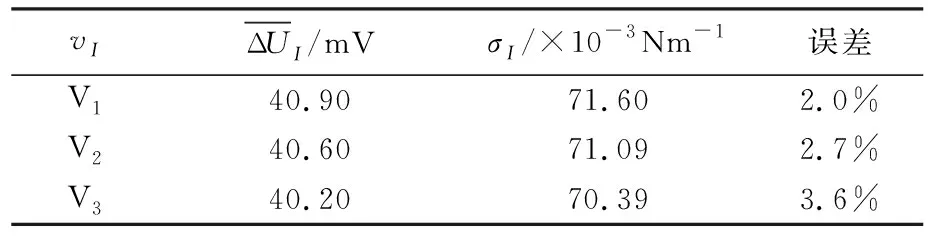
实验中发现,拉脱速度对表面张力系数有着重要的影响。为了研究拉脱速度与水的表面张力系数的关联,本文分别研究3个不同拉脱速度对水的表面张力系数的影响,分别是1.5 mm/min(v1),4.0 mm/min(v2)和12 mm/min(v3),即v1

表2 拉脱法实验数据(v=v1)

表3 拉脱法实验数据(v=v2)

将表2至表4的数据带入公式(3)和(4),从而计算出水的表面张力系数如表5所示。实验时水温为18 ℃,根据文献[11]可知此时水的表面张力系数为σ=73.05×10-3N/m,计算出的实验值误差也显示在表5中。

表4 拉脱法实验数据(v=v3)

表5 不同拉脱速度下的表面张力系数

从表5可见,当圆环匀速上升速度增大的时候,测量出来水的表面张力系数反而减小,测得水的表面张力系数的误差相对越大;反之,圆环匀速上升速度越慢,测得水的表面张力系数值越精确。接下来我们将建立模型,从理论上分析拖拉速度对测量水的表面张力系数的影响。

3 模型的建立与解释

采用COMSOL软件,对圆环相对运动过程中,水膜形态变化进行二维动态仿真,进而解释圆环运动速度对水表面张力系数的影响。由于圆环具有旋转对称性,仿真时选取通过圆环轴线的竖截面(即长方形截面)作为研究对象,截面所在圆环半径方向作为横坐标(记为x),截面轴线方向作为纵坐标(记为y),截面中心处为坐标原点。

3.1 水膜形态变化理论模拟

水膜形态变化仿真如图3所示。图中下半部分为水,上半部分为空气,白色的部分为圆环的截面。水膜的形态变化大致可以分为4个阶段,如图3分别标记为A、B、C、D。

在状态A(稳定状态)情况下,水膜对圆环的力主要表现为水膜对圆环的向下的表面张力的分力、水膜部分的重力以及接触部分附着层的吸引力。随着液面向下运动,即圆环相对向上运动,水膜和圆环之间存在相对的滑移,水膜与圆环侧面的接触面积不断下降,水膜表面与圆环侧面的夹角不断变小,浸润角逐渐变小。因此,附着层的吸引力不断减小,水膜对圆环向下的表面张力分力不断增大。同时由于水膜体积的增加,水膜部分的重力也相应增加。各种效应总体表现为力敏传感器示数的不断增大。在该状态下,水膜很容易保持稳定状态,难以发生破裂。

随着圆环的继续上升,当水膜与圆环侧面的接触面积几乎变为0的时,水膜形态变为B状态(收缩转向状态)。该状态下,水膜逐渐由稳定状态变为非稳定状态。随着圆环的不断上升,水膜的不断拉长,水膜越来越容易断裂。

C状态处于B状态与D状态的交界状态。该状态下,水膜仅仅与圆环底面接触,此时水膜表面与圆环底面的夹角几乎减小到最小值,使得水膜的收缩行为将从角度的变化转换为整体体积上的收缩。

随着圆环相对位置继续提升,则液体与圆环的接触状态D状态(急速收缩状态)。在该状态下,水膜仅仅与圆环底部接触,此时水膜自发收缩效应很显著。液体开始急剧向内收缩,在收缩过程中水膜与圆环底部的接触面不断减小。此时,由于水膜与圆环接触边界的不断减小,表现为表面张力的不断减小直至水膜破裂。该状态下水膜极其不稳定,在无需扰动的情况下就可以自行断裂。

3.2 拉脱速度对水膜形态的影响

由于圆环上升速度的影响,水膜的断裂不仅仅受到水膜稳定状态的影响,还与水膜本身的宏观连续性有关。从宏观层面上来说,水膜在非稳定状态下由于重力以及自身收缩的影响,会发生断裂,但是由于拉动圆环的速度大于水膜本身的收缩速度,使得水膜在进入非稳定状态的时刻不会立刻断裂,而是会短暂地保持宏观的连续性,导致水膜的破裂被延缓。

在拉动速度较小的时候,水膜的断裂更多地取决于水膜自身的收缩。这使得测量的表面张力的数值在表面张力真实值附近浮动,相对比较接近真实的表面张力数值。即水膜更多地会在B阶段的非稳定状态内断裂。

而当拉动速度不断增大的时候,由于拉动速度远远大于了水膜自身的收缩速度,使得水膜断裂的时候与圆环的接触面积已经小于了圆环的底面积,即在C情况下断裂,此时的水膜与圆环的接触边界小于了圆环的内外周长之和,此时的表面张力急剧减小,这造成了拉动圆环的速度很快时,力敏传感器示数偏小表面张力测量值会偏小,从而导致水的表面张力系数减小。

通过以上分析可知,在圆环向上拉动的过程中,圆环底端与液体形成的水膜将逐渐由稳定状态转变向非稳定状态。且随着圆环的不断升高,水膜的不稳定性显著提升,水膜越来越容易断裂。而匀速拉动圆环的速度的增加,则会一定程度上推迟水膜因为不稳定而造成的自发断裂,使得测量出来的表面张力系数偏小。

该模型可以很好的解释圆环与水面拉脱速度越快,表面张力系数越小的原因。同时也表明,实验过程中匀速缓慢的拉脱圆环,有利于更精确的测量水的表面张力系数。

4 结 论

本文研究了拉脱速度对水的表面张力系数的影响,拉脱速度越大,测量出来水的表面张力系数越小,实验误差越大;反之,拉脱速度越缓慢,测得水的表面张力系数的精度越高。本文从水膜形态变化方面详细分析了上述实验结果。当水膜表面与圆环侧面相切时,如果水膜恰好断裂,那么此时测量地表面张力系数更精确。为了能够使得水膜尽可能地接近最佳位置断裂,相对缓慢的拉脱速度,显得尤为重要,同时有利于提高实验的精度。总之,本文研究的不同拉脱速度,为精确测量水的表面张力系数,提供了一条可供参考的实验依据。