基于稳定匹配的网约车合乘优化

彭子烜,魏 然,单文轩,王文思,郭 震,蔡婉君

(1.北京交通大学 交通运输学院,北京 1000441; 2.北京航空航天大学 交通科学与工程学院,北京 102206;3.中国石化化工销售有限公司 华南分公司,广东 广州 510620)

0 引 言

随着“互联网+”和共享经济的蓬勃发展,网约车行业应运而生并迅速扩张。根据中国互联网络发展状况统计调查,2016年末至2018年末,网约车用户规模和用户使用率进入增速迅猛期,截至2022年6月,我国网约车用户规模达4.05亿人,网约车用户使用率达到38.50%。截至2023年1月,获得网约车平台公司获得经营许可已有300多家。网约车的快速发展得益于优惠的价格、良好的乘车体验和高效快速的需求响应。其中,如何快速匹配供需,及时对需求进行响应成为网约车可持续发展的关键。

当前越来越多的网约车平台都推出了拼车服务,它们根据乘客提交的信息(起点,终点,时间),整合相似出行路径的乘客给司机派单。在这种模式下,乘客和司机被动选择接受或拒绝平台的指派。然而,作为利己的乘客和司机,他们更关注如何使自身利益得到最大化,因此,司机对乘客存在选择偏好(比如,司机更偏好搭载收益高的乘客),同理,乘客对司机也存在选择偏好(比如,乘客更偏好与距离近的司机匹配)[1-3]。随着偏好信息的纳入,乘客和网约车匹配机制变得越来越重要。在网约车匹配中,如果忽视乘客和司机双方的选择偏好,不仅会降低他们的满意度,还会影响他们进入匹配市场的动力。因此,有必要提出稳定的匹配机制,在稳定匹配下,任何乘客和司机都无法通过单方面改变匹配对象而获得更高的效益,实现匹配的均衡。

近年来,国内外学者对网络车合乘问题进行了大量的研究[1-3],一部分学者从系统最优视角出发,一部分学者则从均衡视角开展研究[4-5]。D.J. FAGNANT等[6]构建了以最小化乘客等待时间和车内时间为目标函数的网约车匹配模型;在N. AGATZ等[7]的研究中,目标函数是最小化车辆走行距离,通过随机优化方法进行求解,相比于贪婪算法,匹配效率更高;侯立文等[8]建立了多目标合乘模型,分别为乘客效用最大化和司机总行程最小化;QIAN Xinwu等[9]的研究对象包括了出租车和网约车,根据主从博弈方法,研究了两者的竞争关系和均衡状态的存在性;WANG Xing等[2]立足于利己参与人视角,将稳定匹配概念引入到乘客和司机的匹配中,定义并验证了匹配的均衡状态;胡盼等[10]研究了选择出租车出行的影响因素;周乐欣等[11]考虑了网约车定价均衡问题。

稳定匹配的概念是由D. GALE等[12]提出,并在多个领域均有所应用[13-16]。近年来,稳定匹配理论在交通领域得到了一定的应用和推广。在停车匹配方面,HE Fang等[17]研究了车辆-车位稳定匹配问题,并对稳定匹配状态进行了公式化描述,在价格的调整下,系统最优解也能够满足稳定匹配条件;在船货匹配方面,PENG Zixuan等[18]研究了干散货船-货物稳定匹配问题,针对供需平衡、供大于求、供小于求3种场景,设计了价格博弈策略,实现匹配均衡和价格均衡;在航空领域,ZHANG Dapeng等[19]对航线-机场的匹配稳定问题进行研究。

笔者设计了考虑乘客和司机选择偏好的双边稳定匹配,体现了乘客和司机希望能够最大化自身利益,主要创新点在于:①在乘客和网约车的匹配中引入稳定性的概念,将乘客和司机的选择偏好公式化;②在网约车匹配中考虑乘客合乘问题,应用沙普利值对合乘乘客的出行费用进行分摊,构建无偏好假设的多对一稳定匹配模型,并设计算法进行求解。

1 问题描述

在网约车运营中,供给方和需求方分别是司机和乘客。司机作为出行服务的提供者,在系统内的位置是已知的,每个司机可以选择搭载一位或者多位乘客。乘客是出行服务的需求者,提供了起点、终点以及时间窗等出行信息。网约车平台基于以上信息,将乘客进行分组并匹配相应的网约车。乘客分组如图1(a)。图1(a)中,圈内的乘客表示可以合乘出行。假设乘客希望匹配与自己距离近的司机,而司机希望搭载收益高的乘客组。表1展示了司机和乘客组的偏好排序情况。比如,司机1搭载乘客组1的收益要高于搭载乘客组3,因此,他把乘客组1排在第1位。

表1 乘客和司机的偏好排序

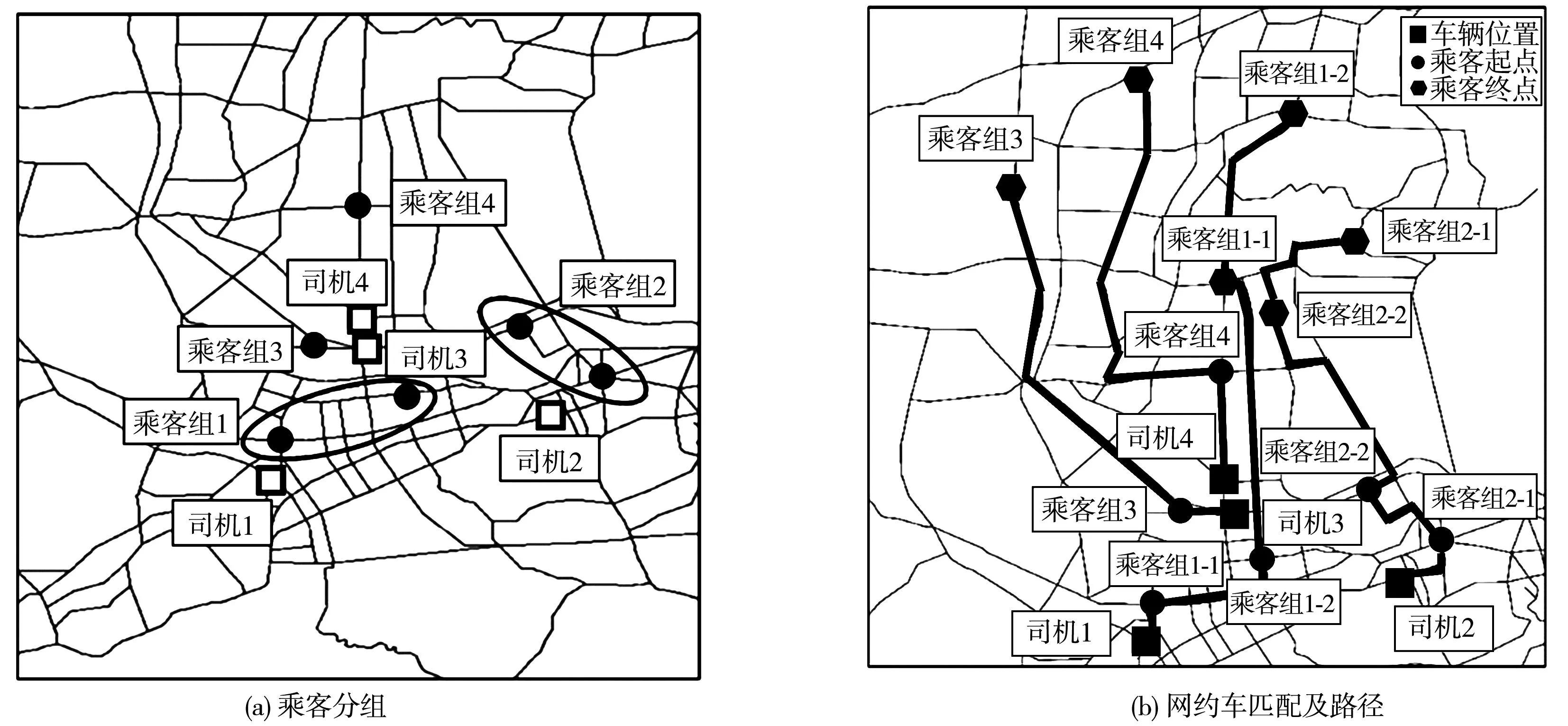
图1 网约车合乘优化

根据以上信息,将乘客组和司机进行匹配。其中,司机1搭载乘客组3、司机2搭载乘客组2、司机3搭载乘客组1、司机4搭载乘客组4是一个可行匹配。但是这个匹配是不稳定的,因为司机1和乘客组1把彼此排在偏好排序的第一位,却没有匹配到一起,他们会拒绝系统指派,选择私下匹配。笔者将司机1和乘客组1称之为阻碍匹配对。而稳定匹配如图1(b),司机到达乘客的起点,将乘客送达目的地。在该匹配中,不存在任何上述的阻碍匹配对。

2 基于稳定匹配的网约车合乘模型

为了便于理解匹配的稳定性,在问题描述中,假设乘客和乘客之间没有选择偏好,但是在实际中,一起合乘出行的乘客之间是存在相互影响的。因此,在构建网约车合乘模型时,打破原有假设,即文中司机对乘客组有偏好,而乘客则同时对司机和合乘乘客组合存在偏好。

2.1 乘客和司机的偏好排序

乘客作为利己的出行者,通常希望出行成本越小越好。当有司机d搭载乘客组ρ时,乘客i∈ρ的出行成本包括了车费和时间成本两部分,如式(1);ρ中的乘客根据沙普利值进行车费分摊,如式(2):

Ci(ρ,d)=Fi(ρ,d)+γ×(TGi-ei) (∀i∈ρ,∀d∈D)

(1)

{ε×[l(s)-l(s′)]} (∀i∈ρ,∀d∈D)

(2)

式中:Ci(ρ,d)为司机d搭载乘客组ρ时,乘客i∈ρ的出行成本;Fi(ρ,d)为司机d搭载乘客组ρ时,乘客i∈ρ付给司机的车费;γ为乘客的时间成本;TGi为司机到达乘客i终点的时间;ei为乘客i的最早出发时间;ρ(i)为乘客组ρ中包含乘客i的所有子集形成的集合;ε为每公里车费单价;l(s)为服务乘客集合s时车辆的最短道路距离;s′为集合s中去除元素i后剩下元素的集合。

令(ρ,d)为一个匹配对,如果乘客i∈ρ在(ρ,d)中的出行成本小于在(ρ′,d′)中的出行成本,那么乘客i更偏好匹配对(ρ,d),乘客的偏好由式(3)表示:

(3)

然而,司机通常希望收益越高越好。当有司机d搭载乘客组ρ时,司机的收益如式(4);同理,司机的偏好由式(5)表示:

(4)

ρd>ρ′d,R(ρ,d)>R(ρ′,d)

(5)

式中:R(ρ,d)为司机d搭载乘客组ρ时的收益;ξ为司机每公里收益。

2.2 稳定匹配模型

网约车合乘不仅可以提高乘客的匹配率,还可以节约乘客的出行里程。而节约出行里程也有利于提高司机的收益。因此,文中目标函数是最大化乘客节约出行里程:

(6)

(7)

(8)

(9)

(10)

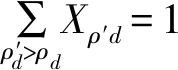
3 算法设计

为了对上述多对一稳定匹配模型进行求解,笔者基于DA(deferred acceptance)算法进行算法设计[12]。DA算法是求解稳定匹配问题的算法之一,该算法可以从任意偏好排序出发,通过请求和拒绝操作,产生一个稳定解。DA算法已广泛地应用于交通问题中,如船货匹配、共享停车匹配、网约车匹配等[9,17-18]。

笔者基于DA算法的思想,设计寻找稳定匹配解的具体流程如下:

Step1:生成初始匹配解:每个参与人自我匹配(匹配对象为自己本身)。

Step2:寻找匹配解:每个乘客i寻找当前还未被拒绝的排名最高的匹配方案。

Step3:寻找阻碍匹配对:遍历每个乘客i和司机d的当前匹配解,寻找是否存在一个阻碍匹配对,如果存在,则该阻碍匹配对中每个参与者均被当前匹配方案拒绝,并转入Step2,否则当一个匹配解中不存在任何阻碍匹配对时,算法结束。

4 案例分析

笔者以大连市为依托进行了算例设计,以验证模型和算法的有效性。大连市路网长402 km,共有个228个节点和383个路段。基于大连市出租车GPS数据得到了乘客的起点和终点以及最早出发时间。由于乘客的时间窗无法获得,假设乘客灵活时间分为两种,一种是紧时间窗,以(0,15)min均匀随机生成,一种是松时间窗,以(5,30)min均匀随机生成。最晚到达时间等于最早出发时间、起终点间的出行时间和灵活时间之和。假设每辆车最多载3位乘客,车速为30 km/h,单位运营成本为0.5元/km。运价为2元/km,乘客的时间成本为26元/h(即大连市人均税前收入除以每月工作小时数)。

4.1 小规模算例

为了说明匹配的过程,首先设计了一个包含2个司机和6个乘客的小规模算例,如图2。假设乘客的时间窗为松时间窗。基于以上信息,可以生成25个匹配对,如表2。以匹配对6为例,司机1匹配乘客1和乘客5。根据司机和乘客在各个匹配对下的收益和成本,得到偏好排序如表3。以司机1为例,最偏好的是匹配对12,即{司机1,乘客1,乘客2,乘客3}。基于偏好排序,计算车辆的载客能力分别为1、2和3时的匹配结果。

表2 匹配对集合

表3 乘客和司机对匹配对偏好排序

图2 小规模算例

当车辆的载客能力为1时,匹配结果如图3(a)。司机1匹配乘客1,司机2匹配乘客2。由于司机的数量少于乘客的数量,在非合乘下,司机更偏好搭载长距离的乘客。通常,长距离的乘客带来的收益更高。当车辆的载客能力为2时,司机1匹配乘客1和乘客5,司机2匹配乘客2和乘客6,如图3(b)。如果司机2搭载乘客3和乘客4,司机1匹配对象保持不变,这也是一个匹配解,但是该解不稳定。因为根据式(9),这个解会被匹配对21所阻碍。当车辆的载客能力为3时,匹配结果如图3(c),即司机1匹配乘客1、乘客2和乘客3,司机2匹配乘客5和乘客6。乘客4由于时间窗限制没有匹配到司机。乘客4仅参与到匹配对16和22中,但是包含这两个匹配对的解均不稳定。综上所述,以上匹配解均是稳定的,即没有乘客或者司机能够通过单方面改变匹配对象获得更高的效益。

4.2 不同规模算例

笔者设计了不同规模的算例,算例的需求分为低需求(A)和高需求(B),算例包含了司机的数量,乘客的数量和时间窗。如300-600-r代表算例中有300 位司机和600位乘客,乘客时间窗为松时间窗。不同规模算例的计算结果如表4。首先,从时间窗的角度进行结果分析,松时间窗下乘客的匹配率较高,同时乘客合乘比例也有所增加。这是因为乘客的时间窗松弛后,降低了时间约束的影响,增加了乘客合乘的可能性,乘客匹配率平均提高18%,合乘比例平均提高21%。乘客合乘有利于增加司机的平均收益,但是随着乘客合乘的比例增加,乘客的平均等待时间也有所增加,同时可能发生一些不可避免的绕行,使得绕行比例增加。然后分析低需求(A)和高需求(B)下的计算结果,需求增加了两倍后,司机匹配率增加,乘客合乘的比例有了大幅提升,同时司机的收入也有所提高。乘客的需求影响了合乘的可能性,参与的乘客越多,合乘的可能性就越大。

表4 不同规模的计算结果

5 结 论

笔者在研究网约车合乘问题时,考虑了利己乘客和司机希望实现自身利益的最大化,基于合乘乘客间的相互影响,构建了多对一稳定匹配模型并设计了相应的算法和不同规模的算例进行分析,得到以下主要结论:

1)提出合乘模式下乘客和司机稳定匹配模型。通过计算结果可得,非合乘模式下,司机受收益驱动更偏好于搭载出行距离较长的乘客。在供给小于需求时,出行距离相对较短的乘客处于劣势地位,出行需求难以被满足。合乘模式下,随着载客能力的提升,乘客的匹配率增加,但由于合乘出行时绕行不可避免,在时间窗的约束下,部分乘客合乘出行受限。在有限运力下,合乘模式可以增加乘客的匹配几率,减少乘客总出行里程,降低碳排放。

2)时间窗和参与人数量对合乘模式下的匹配率尤为重要。随着乘客时间窗的松弛,形成了更多的合乘出行方案,乘客匹配率平均提高18%,合乘比例平均提高21%。同时,高需求放大了乘客匹配率和合乘比例的提升幅度,与低需求相比,高需求下的提升比例是低需求的2倍之多。在打车需求旺盛时段,是可以通过合乘缓解打车难题,而且高的需求也为合乘提供了有利条件,乘客可以通过释放一定时间窗要求以提高匹配的概率,降低等待时间。