宽幅分离式双边钢箱组合梁斜拉桥剪力滞效应研究

于祥敏,刘 进,杜晓庆,2,倪 铮

(1.上海大学 力学与工程科学学院, 上海 200444; 2.上海大学 风工程和气动控制研究中心, 上海 200444;3. 中国建筑基础设施有限公司, 北京 100000)

0 引 言

钢-混组合梁斜拉桥充分利用钢材抗拉强度高和混凝土抗压能力强的性能优势,具有自重轻、跨越能力大、施工便利、造价低等优点[1-2],在300～700 m的大跨度桥梁中具有很强的竞争力。组合梁斜拉桥常用钢主梁形式为双边工字梁、双边小箱梁和单箱多室箱梁,随着我国经济发展和交通量快速增长,近年来开始采用新型的分离式双边钢箱组合梁以适应更宽的6～8车道需求,例如望东长江大桥和椒江二桥。分离式双边钢箱组合梁斜拉桥的桥面宽度大、横向刚度大、抗风性能好,兼具槽型单箱组合梁与矩形双箱组合梁的优点,在宽幅大跨径斜拉桥中应用前景广阔[3]。

分离式双边钢箱组合梁斜拉桥在荷载作用下会产生明显的剪力滞现象,在实际的设计分析中如未考虑剪力滞,会高估主梁承载能力,容易导致桥面板开裂等安全隐患[4-7],所以有必要对其进行剪力滞效应的分析。国内外学者对此做了大量的研究,刘洋等[8]基于能量变分法及矩阵分析法研究了П形工字钢-混凝土组合梁斜拉桥施工过程中的剪力滞效应;朱力等[9]通过虚功原理和有限差分法提出了钢-混凝土组合箱型梁考虑滑移和剪力滞效应的理论模型;WANG Chunsheng等[10]通过试验研究了组合梁斜拉桥在不同荷载作用下的剪力滞效应,并建立了考虑滑移效应的有限梁段模型;ZHU Li等[11]通过试验分析了组合梁桥面板的剪力滞效应,确定了其有效宽度的纵向分布特性,并提出有效宽度的预测公式。

综上可知,现有组合梁剪力滞效应研究多针对双边工字梁组合梁及双边小箱梁组合梁,鲜有对分离式双边钢箱组合梁剪力滞效应的研究。基于此,笔者通过有限元数值计算法,建立分离式双边钢箱组合梁斜拉桥的杆系模型及节段精细化模型,研究其成桥状态及施工过程中的剪力滞效应,并通过参数敏感性分析研究钢主梁的板厚对剪力滞效应的影响,为类似工程提供借鉴和参考。

1 工程背景

文中的背景工程为一座双塔双索面半漂浮体系的分离式双边钢箱组合梁斜拉桥,跨径布置为(95+220+95)m=410 m,如图1。该桥采用单层桥面布置,双向八车道城市公路,设计行车速度为80 km/h。车辆荷载等级为公路—Ⅰ级,结构设计安全等级为一级。全桥主梁共划分为49个梁段,标准梁段采用桥面吊机悬臂拼装,包括边跨B2～B7和中跨Z2～Z11节段。每节标准梁段长度为9 m,最大起吊重量约为290 t。索塔区梁段0#块(B0-1/B0-2/Z0-1/Z0-2)和1#块(B1/Z1)采用浮吊架设,边跨现浇梁段(B8/B9)采用支架安装。

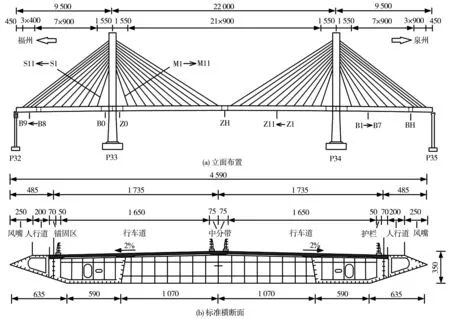
图1 桥型布置 (单位:cm)

标准梁段由混凝土板、分离式双边钢箱、横隔板、小纵梁等组成。主梁中心线处梁高3.5 m,全宽45.9 m(含风嘴),建成后将成为国内最宽的分离式双边钢箱组合梁斜拉桥。其中,钢箱梁中心线处梁高3.1 m,由双边箱、横隔板及加劲肋等组成。混凝土板标准厚度为0.28 m,在钢梁腹板附近变厚至0.40 m,标准梁段的具体构造与详细参数见图2。主塔为H形,塔高110 m,索塔顶宽40.7 m,设置上下两道横梁。全桥共2×4×11=88根平行钢丝斜拉索,最长索长为122.75 m,重约9.4 t,梁上标准索距为9 m。

图2 标准梁段构造 (单位:mm)

2 有限元方法

2.1 模型验证

有限元分析的结果受模型材料、网格尺寸、边界条件等影响。笔者为了验证有限元方法的可靠性,针对文献 [12] 和文献 [13] 中的工字形(模型1)和双边工字形组合梁(模型2)进行了模拟验证。图3为所选模型的关键信息,包括模型的材料特性(E为弹性模量,γ为泊松比,ρ为密度)、模型的跨径、施加的荷载、边界条件及横截面的具体尺寸。模型中的混凝土板都采用SOLID45实体单元模拟,钢主梁采用SHELL43壳单元模拟,钢主梁与混凝土板之间采用完全抗剪连接。

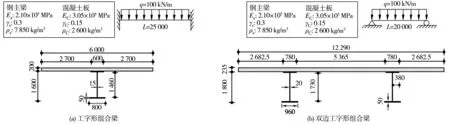
图3 验证模型几何参数和材料特性 (单位:mm)

图4给出了有限元分析结果,包括模型1混凝土板的竖向挠度和模型2跨中截面混凝土板的应力。对于两端固结的工字形组合梁,在均布力荷载作用下,跨中位置处的竖向挠度最大,两端位移几乎为0,如图4(a)。文中结果与文献[12]计算结果的平均比率为97%,标准偏差为4.1%。对于两端简支的双边工字形组合梁,均布力荷载作用下混凝土板处于受压状态,工字形钢梁顶压应力最大,跨中和两端压应力最小,如图4(b)。文中结果与文献[13]计算结果的最大误差为7.85%,标准偏差为5.04%。综上可知,文中结果与所选模型的结果吻合良好,证明了有限元方法的可靠性。

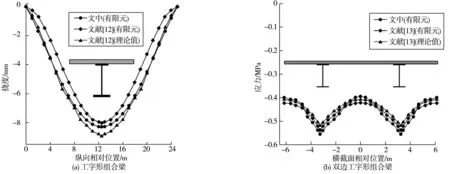
图4 验证模型结果对比

2.2 有限元分析

笔者首先采用MIDAS CIVIL建立背景工程的全桥杆系模型,进行整体计算分析,得到成桥状态和施工过程中按初等梁理论计算的钢箱梁及混凝土板应力,考虑结构自重、斜拉索索力、预应力、汽车荷载、人群荷载、温度和基础沉降等作用。其中,主梁、主塔和桥墩均采用梁单元模拟,斜拉索采用桁架单元模拟,全桥模型共581节点,488单元,如图5(a)。在整体计算分析时,首先通过索力优化得到理想成桥状态,再进行施工全过程仿真分析,并按GB 50917—2013《钢—混凝土组合桥梁设计规范》进行荷载组合,取最不利基本组合进行计算分析[14-15]。模型采用的主要材料参数详见表1。

图5 有限元模型

进一步,采用ANSYS建立背景工程的三维节段精细化模型,进行主跨梁段的局部分析,以得到钢箱梁及混凝土板的应力分布情况。考虑到结构及荷载都对称,建立一半的结构模型以提高计算效率。为了降低边界效应的影响,建立了中跨的5个主梁节段,模型全长45 m,宽度为18.7 m,如图5(b) 。其中,钢主梁和锚拉板采用壳单元SHELL63模拟,混凝土桥面板用实体单元SOLID95模拟,预应力采用LINK8。钢主梁的网格尺寸为250 mm,混凝土桥面板的网格尺寸为300 mm,模型共359 052节点,190 495单元。钢主梁与混凝土桥面板之间面面绑定约束来进行传力,斜拉索索力采用节点力形式施加到锚拉板上,二期恒载通过面荷载的形式施加到混凝土板上,纵向和横向预应力荷载通过升降温的形式施加到混凝土板上。模型的边界条件为:横向对称面上施加对称约束,主梁一端施加固定约束,另一端施加边界荷载,边界荷载提取自MIDAS CIVIL中相应工况及截面的轴力、弯矩和剪力。

3 成桥状态剪力滞效应

图6给出了成桥状态不同节段主梁混凝土板的应力分布。可以看出:荷载组合下,混凝土板处于受压状态,且越靠近塔根的节段,压应力越大;混凝土板承受的最大压应力为-14 MPa,未出现拉应力,满足规范要求;混凝土板顶的应力分布受主梁节段位置影响较大,板底受影响较小。

图6 成桥状态混凝土板的应力分布 (单位:MPa)

图7给出了成桥状态不同节段混凝土板的应力比和剪力滞系数结果,可以看出:混凝土板底和板顶的剪力滞系数变化范围分别为2.152～2.762和1.262～2.024,混凝土板底的剪力滞效应更为显著;从顺桥向来看,越靠近跨中节段,混凝土板的剪力滞系数越大,最大剪力滞系数为Z11节段。从横断面来看,在边腹板、中腹板和小纵梁位置处,混凝土板正剪力滞效应显著,横隔板顶的混凝土板则主要呈现负剪力滞效应。

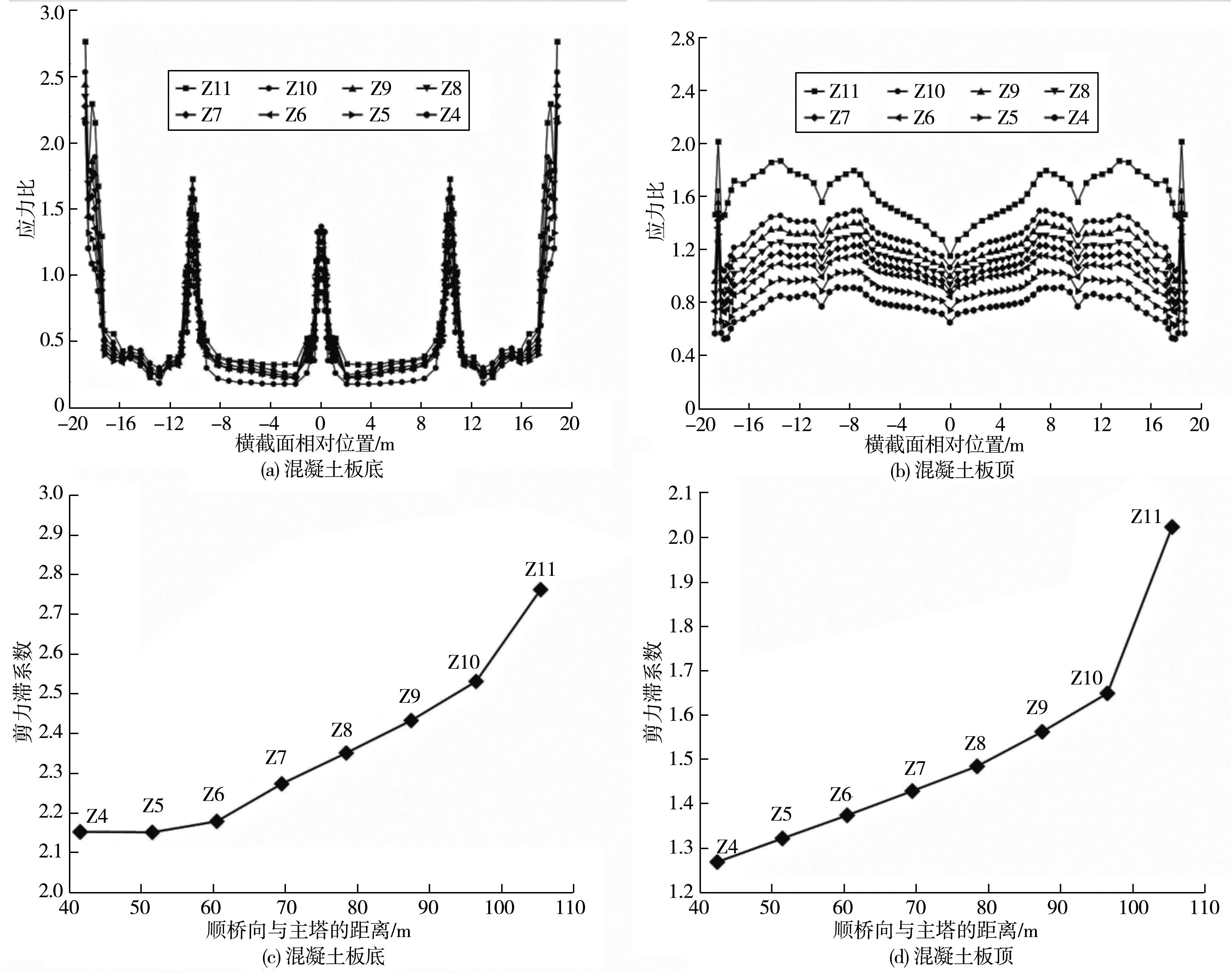
图7 成桥状态混凝土板应力比和剪力滞系数

混凝土板顶、底部的应力比分别在0.234～2.762和0.531～2.024范围内变化;混凝土板底的应力比在边腹板、中腹板及小纵梁位置处会增大,而混凝土板顶在这些位置处会减小。受斜拉索水平分力影响,混凝土板在主梁两端的应力比最突出。

4 施工过程剪力滞效应

在施工过程中,主梁标准梁段的施工步骤为:桥面吊机前移→钢梁节段吊装→斜拉索一张→预制桥面板安装→湿接缝浇筑养护→斜拉索二张→循环进行下一节段施工。

图8给出了最大悬臂梁端梁段Z11施工时,Z10梁段混凝土桥面板的应力比和剪力滞系数结果。可以看出:施工过程中,混凝土板底和板顶的剪力滞系数范围分别为3.978～4.188和1.186～1.301;施工步骤对组合梁剪力滞效应影响显著,其中钢主梁吊装影响最大,混凝土板铺装影响最小;随着施工的进行,组合梁各部位的应力比分布规律相似,在边腹板、中腹板及小纵梁位置处的混凝土板的应力比都会产生较大的变化,这一点与成桥状态的规律相似;Z11梁段施工时,Z10梁段混凝土板底在边腹板、中腹板、小纵梁位置处主要为正剪力滞,其余位置为负剪力滞。混凝土板顶在边腹板、中腹板及小纵梁位置处则为负剪力滞,其余位置为正剪力滞;混凝土板底的剪力滞效应比板顶明显,这是因为板底与钢主梁连接,共同作用的影响。

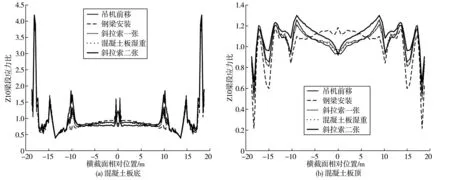
图8 施工过程中混凝土板应力比和剪力滞系数

5 板厚对剪力滞效应的影响

为了研究钢主梁板厚对剪力滞效应的影响,以最大悬臂梁段Z11为对象,钢主梁顶、底板各选取6种不同板厚进行对比分析,板厚分别为10、15、20、25、30、35 mm。

由于应力比能很好地反映横截面的剪力滞效应,图9和图10给出钢主梁顶板和底板分别变厚时混凝土板的应力比。可以看出:板厚变化时,剪力滞系数变化规律相似,不改变剪力滞特征。顶、底板厚度分别为25 mm和15 mm时,组合梁的剪力滞效应最小;综合考虑板厚及剪力滞效应的影响,钢主梁顶、底板合理厚度范围分别为20～30 mm和15～20 mm。

图9 底板变厚时对混凝土板应力比影响

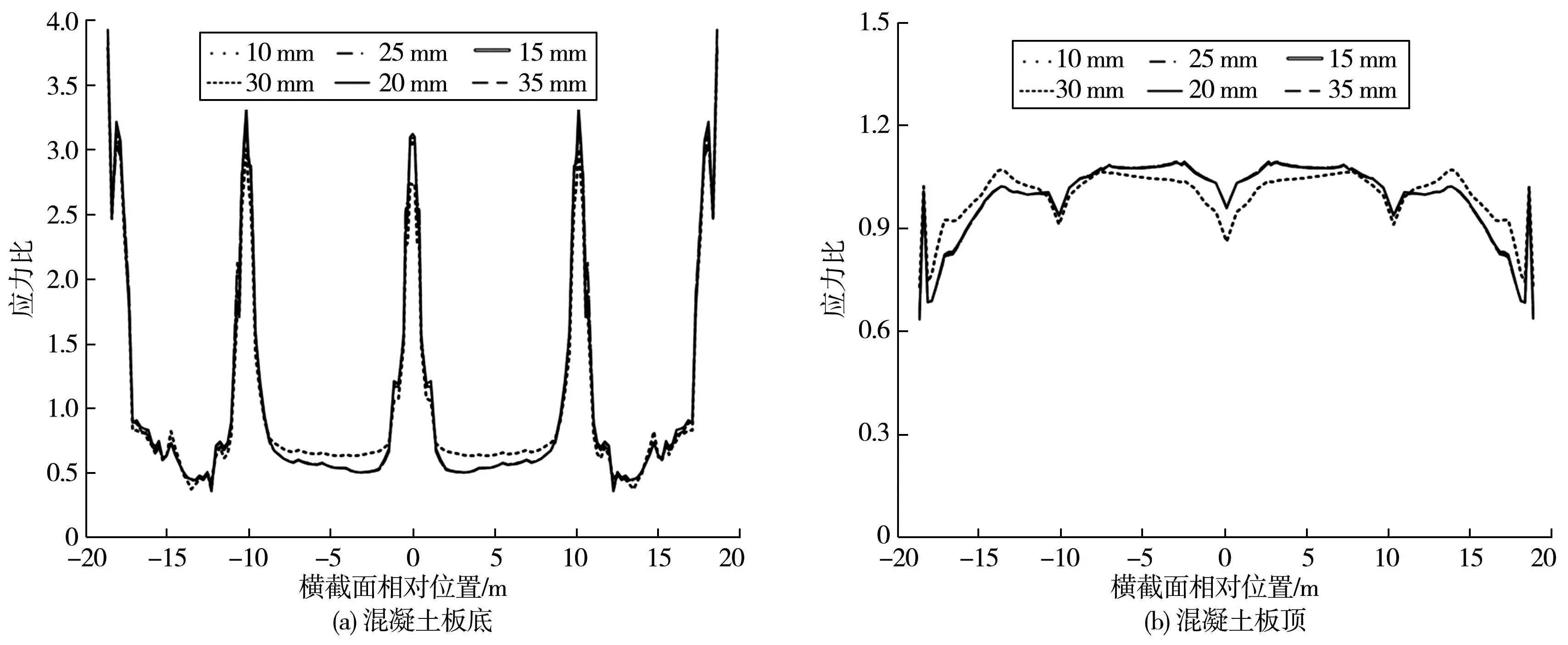
图10 顶板变厚时对混凝土板应力比影响

6 结 论

以梁宽为45.9 m的超宽分离式双边钢箱组合梁斜拉桥为研究对象,研究其成桥状态和施工过程中的剪力滞效应及板厚影响,得到的主要结论如下:

1)荷载组合作用下,组合梁的混凝土板承受的最大压应力为-14 MPa,未出现拉应力,满足规范要求;越靠近塔根的节段,混凝土板的压应力越大。

2)成桥状态下,混凝土板底和板顶的剪力滞系数变化范围分别为2.152～2.762和1.262～2.024。从纵桥向来看,越靠近跨中节段,混凝土板的剪力滞系数越大,最大剪力滞系数为Z11节段;从横断面来看,在边腹板、中腹板和小纵梁位置处,混凝土板正剪力滞效应显著,横隔板顶的混凝土板则主要呈现负剪力滞效应。受到斜拉索水平分力的影响,混凝土板两端的剪力滞效应最突出。

3)施工过程对组合梁剪力滞效应影响显著,混凝土板底和板顶的剪力滞系数范围分别为3.978～4.188和1.186～1.301。混凝土板底的剪力滞效应比板顶明显,需要重点关注。

4)钢主梁板厚变化时,剪力滞系数变化规律相似,不改变剪力滞分布特征。建议钢主梁顶板厚度和底板厚度取值范围分别为20～30 mm和15～20 mm。