关于J.Warburton方法的钢丝交叉磨痕体积计算及误差分析
2023-12-26刘怡杉吴景亮韩飞燕
张 武,刘怡杉,吴景亮,韩飞燕
(西安科技大学机械工程学院,陕西 西安 710054)
1 引言
钢丝绳是一种柔性的三维环绕结构钢制品,作为最重要的挠性构件之一,由于其具有抗拉强度和抗疲劳强度高等许多优点,在矿井提升、索道缆车、交通运输等领域得到广泛应用。钢丝绳的损伤情况和承载能力,时刻关系到设备和人身安全[1]。文献[2]提出了垂直相交和不同角度相交时圆柱在特定磨损条件下的磨损体积计算。文献[3]提出了钢丝绳不均匀磨损量的计算方法和范围,并且可以通过预测钢丝绳的磨损情况来确保安全。文献[4-5]进行了不同微动条件下不同交叉角度的钢丝磨损试验,用表面轮廓仪分析了磨痕体积,基于Archard系数引入平均摩擦系数,得到磨损体积数学计算公式。文献[6]讨论了不同微动参数下钢丝的微动磨损行为,对钢丝间磨损体积提出多种数学积分方法,结果表明在理想情况下磨损量是可以用数学公式表达的。文献[7]对不同条件下的细钢丝进行了不同的微动试验,测定了试样的体积磨损。文献[8]通过大量磨损试验,得出了不同磨损时间条件下,上钢丝磨痕形状近似为圆形,下钢丝磨损形状近似为椭圆,这与文献[4-5]的实验结果吻合。文献[9]提出了一种有限元方法来模拟圆柱与平面接触时的微动磨损及磨损量。文献[10]对圆柱在平面上往复接触状态下进行了磨损预测与仿真,并将模拟结果与实验结果建立了良好的相关性。所采用的方法与Podra的有限元仿真方法类似[11]。
文献[12]对旋转钢丝绳的疲劳失效进行了研究,结果显示钢丝失效主要发生在相邻钢丝绳之间的磨损部位,单根钢丝的主要失效机理被认为是磨损部位接触应力的函数。文献[13-15]对钢丝的微动损伤过程进行了试验,考察了接触载荷和微动时间对磨损深度的影响,研究显示磨损深度随着接触载荷和微动频率的增加而呈增长趋势。文献[16-18]通过建立微动磨损演化模型,分析了钢丝绳在不同使用寿命阶段的受力状态和钢丝间位移,并对钢丝微动的疲劳寿命进行了估算。文献[19]的研究显示随着接触表面间接触应力的增大,磨痕的深度和宽度也随之增大。并且以摩擦系数和磨损深度作为评定微动磨损的参数,考察了不同载荷下摩擦系数的变化规律以及载荷、循环次数的变化对钢丝试样磨损深度的影响。文献[20]研究了单根钢丝的微动磨损和微动疲劳,得出由微动引起的变形、磨损和裂纹是导致钢丝失效的主要原因[20]。文献[21]以(6×19)热镀锌钢丝绳为研究对象,对不同载荷、滑移速度、冲击速度下钢丝绳滑动摩擦磨损规律及接触区域与温度变化之间的规律进行试验探究。文献[22]提出了一种包含摩擦和Archard磨损定律的弹性接触算法,分析了微动过程中的接触压力演化,指出在显式磨损计算中数值存在不稳定性,并给出了一种稳定判据[22]。
以文献[2]的研究为基础,主要进行理想磨痕状态下,直线型钢丝接触、直线型钢丝与圆弧型钢丝接触时的磨痕体积计算和误差分析。
2 直线型钢丝交叉时磨痕体积解析计算
两个直线型钢丝交叉磨痕体积计算按照交叉角度的不同分为两种:一种是交叉角度等于90°(θ=90°),另一种是交叉角度不等于90°(θ≠90°)。这主要是因为在进行体积计算过程中,当θ≠90°时需要引入三角函数参与计算。磨痕的几何形状是两个直线型钢丝交叉重叠的部分,其主要是由两个非完整的圆柱面形成,因此在计算过程中主要采用解析几何和积分的方法。该方法与J.Warburton的研究相似,都是将磨痕的形状当成几何问题研究。钢丝选用相同的线性弹性材料制成,不考虑任何摩擦学效应和影响磨痕形状的因素。
2.1 θ=90°时的J.Warburton磨痕体积计算
无论θ=90°还是θ≠90°,两个钢丝磨痕均呈现出椭圆形轮廓,同时轮廓在任意深度h处为可近似为平行四边形,如图1所示。如果最大磨痕宽度为C,任意深度h处的宽度为c;最大磨痕长度为Cʹ,任意深度h处的长度为c',则矩形面积为ccʹ。
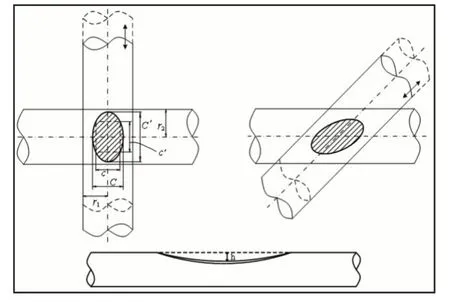
图1 直线型钢丝磨痕示意图Fig.1 Schematic Diagram of Straight Wire Wear Scar
在微动磨损过程中,用最大磨损深度表征微动磨损。则最大磨损深度与最大磨损宽度的关系为:
如图可以得出磨痕体积计算公式:
将式(4)从式(3)中省略,则磨痕体积V为:
式中:V—磨痕体积;H—两个接触钢丝的总磨痕深度;r1、r2—两个接触钢丝的半径。
2.2 θ≠90°时的J.Warburton磨痕体积计算
当钢丝交叉角度θ≠90°时,磨痕轮廓同样可近似为平行四边形,其面积可由cc'×cscθ来表达。因此,钢丝交叉角度θ≠90°时的磨痕体积V可表示为:
3 直线型钢丝与圆弧型钢丝交叉磨痕体积解析计算
两个半径相同的直线型钢丝,将其中一个直线型钢丝进行弯曲得到半径为r3的圆弧形钢丝,此时直线型钢丝与圆弧形钢丝接触磨损,如图2所示。其磨痕体积由A、B两部分组成。
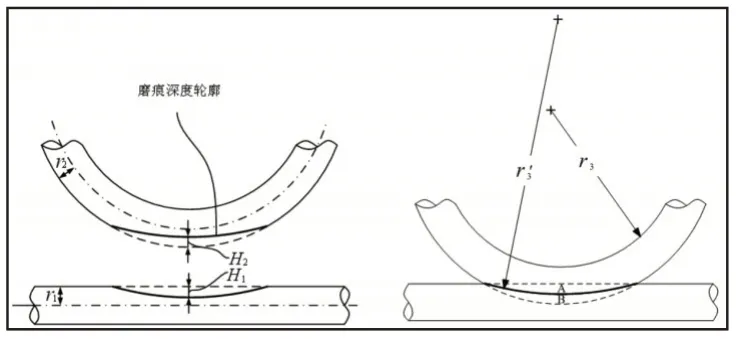
图2 直线型钢丝与圆弧型磨痕示意图Fig.2 Schematic Diagram of Straight Steel Wire and Arc-Shaped Wear Scar
根据直线型钢丝和圆弧形钢丝的接触几何关系,相关参数表达如下:
式中:H1—直线型钢丝上的磨痕深度;H2—圆弧形钢丝上的磨痕深度,—磨痕曲线的曲率半径;—B磨痕区域上的一个有效半径。
则直线型钢丝与圆弧形钢丝交叉总磨痕体积为:
最终得到VA和VB部分体积公式:
4 直线型钢丝交叉时磨痕体积数值计算及误差分析
4.1 误差定义
根据以上内容,可以明显地看出由于I的省略导致钢丝磨痕体积与真实体积之间存在误差。因此,我们将主要用数值方法和J.Warburton方法对钢丝磨痕体积进行计算和对比(其中数值计算结果为真值),同时根据绝对误差和相对误差来判断省略I所带来的钢丝磨痕体积误差数值及规律。采用数值方法时,使用三维软件进行实体绘图,根据剪切材料的方法得出规则的磨痕,如图3所示。数值方法的体积可被定义为:
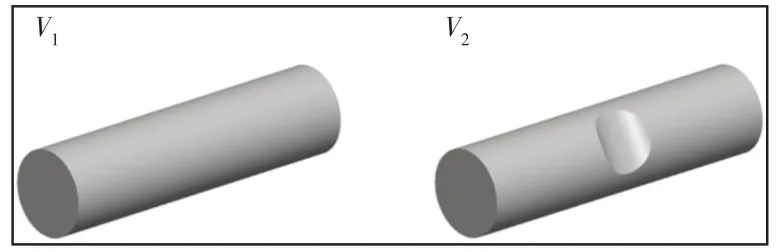
图3 三维实体模型Fig.3 The 3-Dimensional Solid Models
绝对误差Vae和相对误差Vre的定义如下:
4.2 θ=90°时的直线型钢丝磨痕体积数值计算及误差分析
θ=90°时的直线型钢丝磨痕演化规律,如图4所示。图4(a)为磨痕表面轮廓线,图4(b)为磨痕深度轮廓线。当θ=90°时,不同的磨损深度会产生不同的磨痕轮廓。图4(a)为磨痕表面轮廓线演化规律,磨痕间距随着磨损深度的增加而减小,这主要是由两个钢丝接触面积逐渐增大而导致,其磨痕表面形状也由近圆形向四边形发展。图4(b)为磨痕深度轮廓线演化规律,其磨痕形状始终保持圆形。
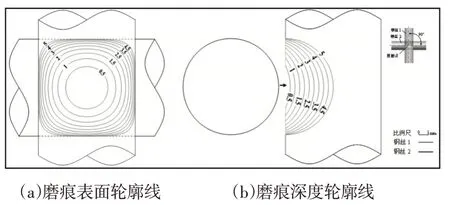
图4 直线型钢丝交叉磨痕的演变(θ=90°)Fig.4 Evolution of Wear Scar in Crossed Linear Steel Wires(θ=90°)
选取r1=r2=5mm,Hmax=5mm 时,由数值方法和J.Warburton 方法分别计算得到的体积数值,以及绝对误差和相对误差,相关数值,如表1所示。
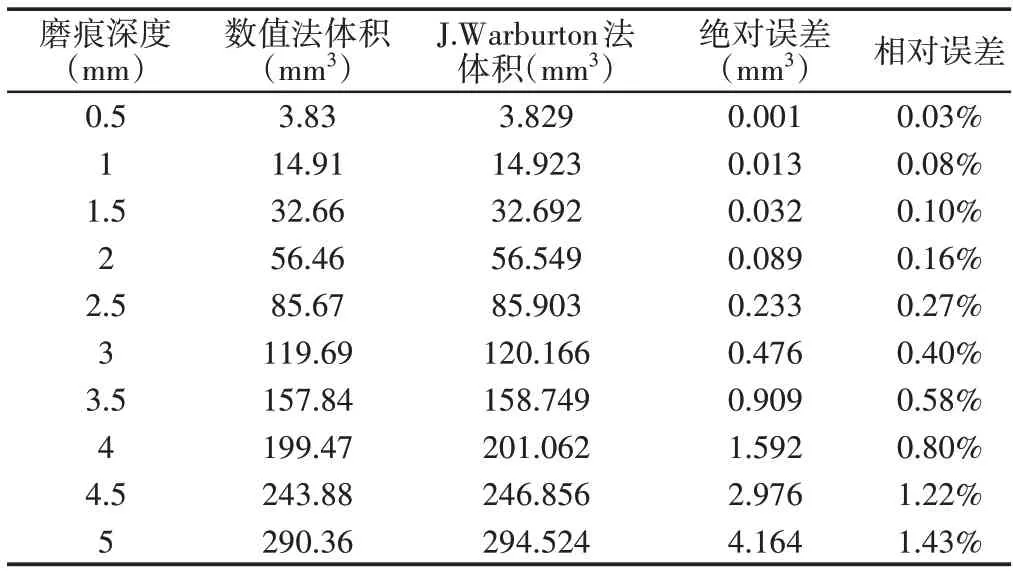
表1 体积计算和误差值(θ=90°)Tab.1 Calculated Volume and Error Values(θ=90°)

表2 主要符号表Tab.2 Main Symbols Table
根据所得数据,得到的磨痕体积和误差变化规律,如图5所示。
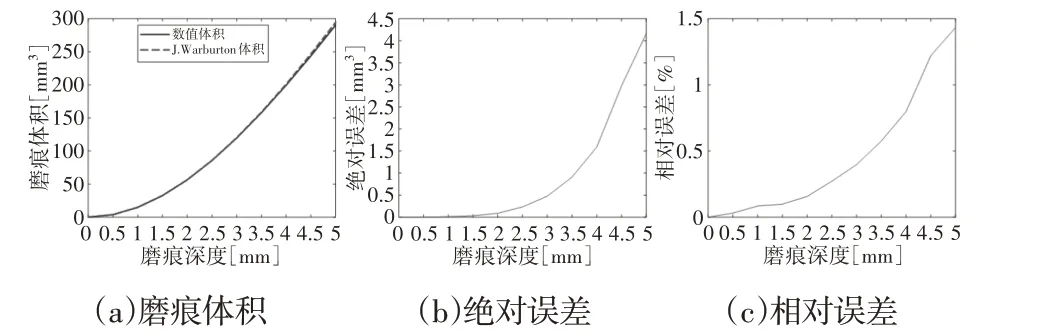
图5 磨痕体积和误差(θ=90°)Fig.5 Wear Scar Volume and Error Versus Depth(θ=90°)
图5(a)中当磨痕深度增大时,两种方法所得的磨痕体积也相应增大。J.Warburton方法所得到的磨痕体积始终大于数值方法得到的磨痕体积,通过分析认为,J.Warburton方法所省略的I项是一个负值,因此,J.Warburton方法对磨痕体积的计算是把体积放大了。图5(b)和图5(c)显示随着磨痕深度的增大,绝对误差和相对误差均增加。当磨痕深度达到2.5mm时,J.Warburton方法省略I项所带来的误差仅为0.27%,之后则随着磨痕深度的增大误差则极具增大,当磨痕深度达到5mm时,J.Warburton方法省略I项所带来的误差为1.43%。因此,当磨痕深度超过钢丝半径的一半时,J.Warburton方法所带来的体积误差将必须予以考虑。
4.3 钢丝间交角θ≠90°误差分析
θ=60°、θ=45°、θ=15°时磨痕体积和误差变化规律,如图6~图8所示。由图可以看出类似的误差变化规律同样发生在θ≠90°时。由于绝对误差的增长速度较慢,同时Vn增长幅度较大,最后导致相对误差的减小,所以磨痕深度为1mm的相对误差小于磨痕深度为0.5mm的相对误差,如图7所示。无论θ如何变化,由于省略了I项的原因,J.Warburton方法所得的磨痕体积大于数值方法。当磨痕深度超过2.5mm时,绝对误差和相对误差极具增大,最大误差为1.43%。因此,当磨痕深度超过钢丝半径的一半时,J.Warburton方法所带来的体积误差将必须予以考虑。
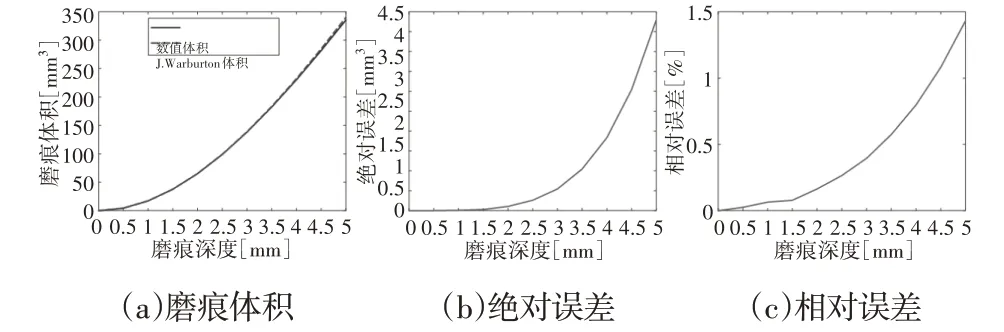
图6 磨痕体积和误差(θ=60°)Fig.6 Wear Scar Volume and Error Versus Depth(θ=60°)
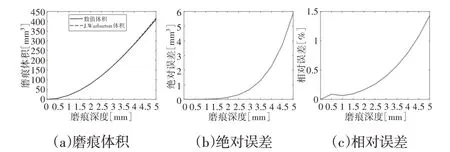
图7 磨痕体积和误差(θ=45°)Fig.7 Wear Scar Volume and Error Versus Depth(θ=45°)
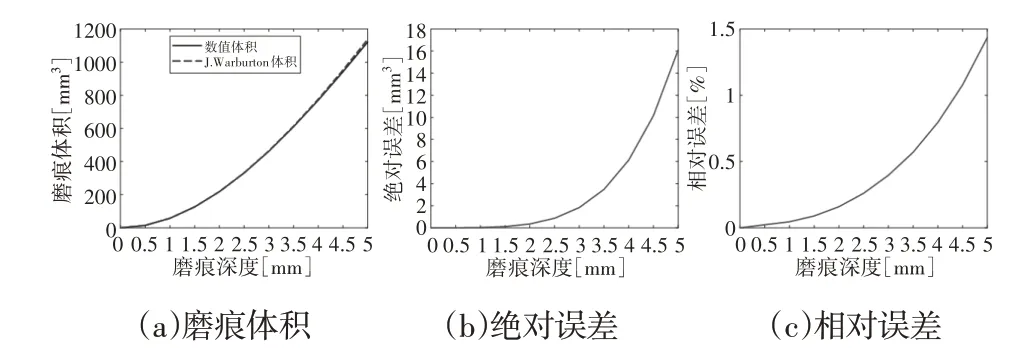
图8 磨痕体积和误差(θ=15°)Fig.8 Wear Scar Volume and Error Versus Depth(θ=15°)
5 直线型钢丝与圆弧型钢丝磨痕体积数值计算及误差分析
A部分体积可以由式(12)准确的计算,如图2所示。结合式(11)、式(13)可得直线型钢丝与圆弧型钢丝磨痕体积及误差。此处暂不考虑省略I项带来的误差。
为了更加清晰的表现误差造成的影响,在此部分选用r1=100mm的规格进行计算。r3=nr1(n>2)时,直线型钢丝与圆弧型钢丝交叉磨痕体积和绝对误差的变化规律,如图9所示。由图可以看出,对于某个固定的倍数,绝对误差随着磨痕深度的增大而增大。由图10可以看出,相对误差随着磨痕深度的增大而增大,随着n的增加而减小,当n=2.01时,相对误差最大,数值为10.25%;当n=10时,相对误差数值为1.73%。分析认为,r3*参与计算的VB不能真实的反映B磨痕的体积,导致J.Warburton方法计算结果与数值方法相差甚远。因此,J.Warburton对B磨痕的体积用式(13)来表达持怀疑态度是正确的。
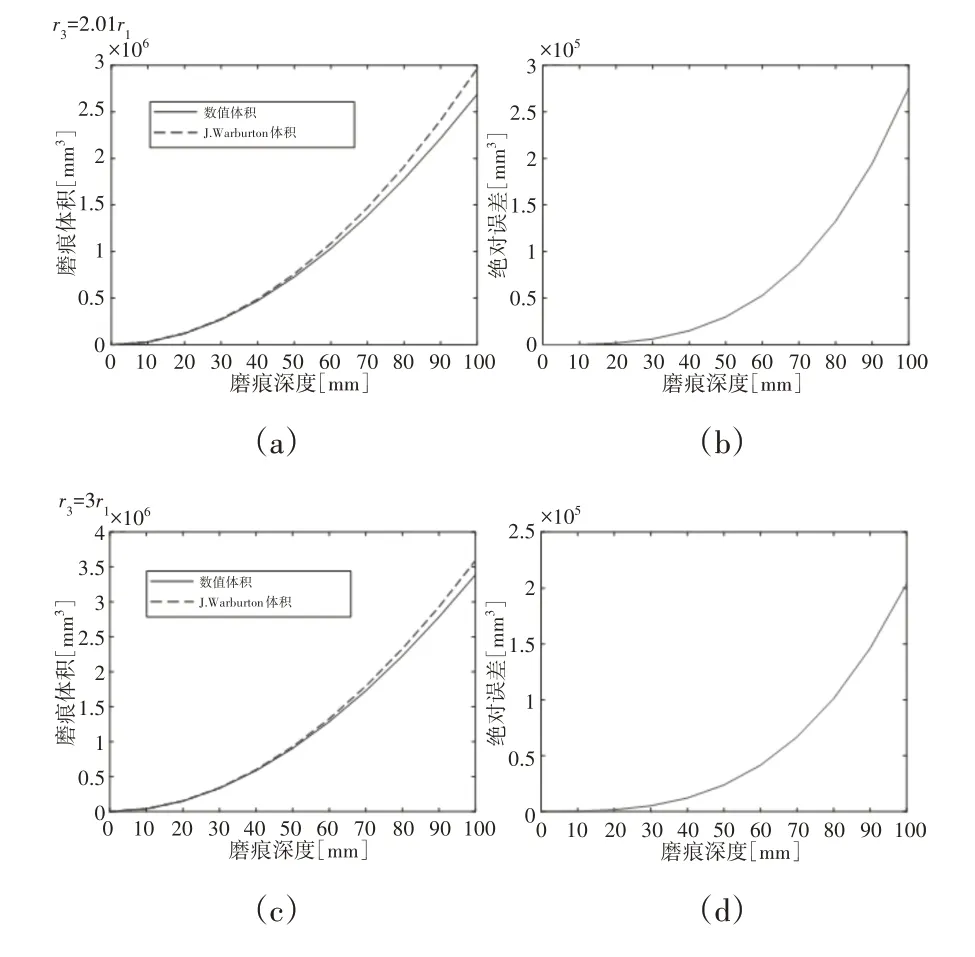
图9 不同圆弧线弯曲半径下两种方法的磨痕体积和绝对误差Fig.9 The Wear Scar Volumes and Absolute Errors at Different Wear Scar Depths and at Different Radii of Curvature of the Circular Arc-Wire
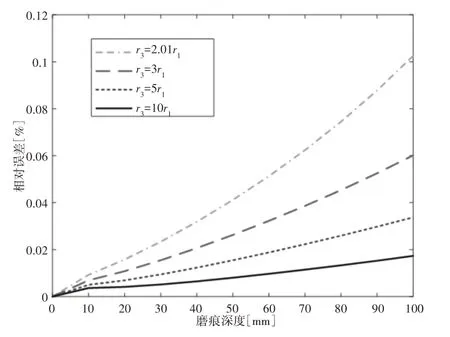
图10 不同圆弧线弯曲半径下的相对误差Fig.10 Relative Error at Different Radii of Curvature of the Circular Arc-Wire
对B部分的体积进行反验证,以此来说明式(13)不能准确表达B磨痕的体积。因为A部分的面积可以准确的计算出,同时结合式(11),根据数值方法可得出B部分的体积,进而可以得出一个综合半径,定义为r*,r*和r3*在n取不同值时的变化规律,如图11、图12所示。由图11、图12可以看出,当n=2.01时,相对误差为42.21%;当n=10时,相对误差为6.98%。由图12可以看出,无论n取多少,随着磨痕深度的增大,固定倍数下的相对误差都是不断增大。对于相同的磨损深度,n越大,相对误差越小。但是,无论n如何变化,随着磨损深度的增加,r*不断减小,r3*不断增大,两者呈现出截然相反的规律。通过式(10)确实可以计算出r3*,但是r3*参与计算的VB不能反映B磨痕的真实体积。因此,1986年,J.Warburton对B磨痕的体积用式(13)来表达持怀疑态度是正确的。
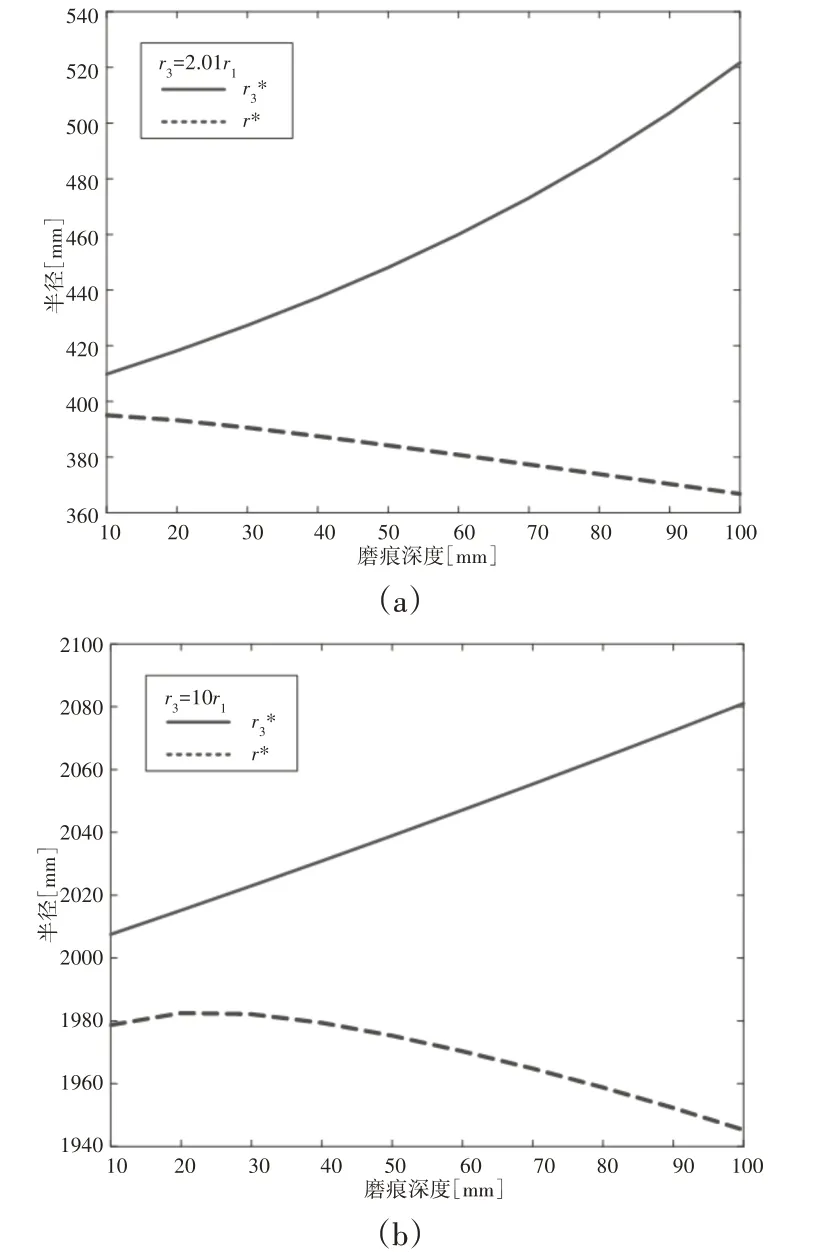
图11 r*和r3*的变化规律Fig.11 The Variation ofr* andr3* withWear Scar Depth
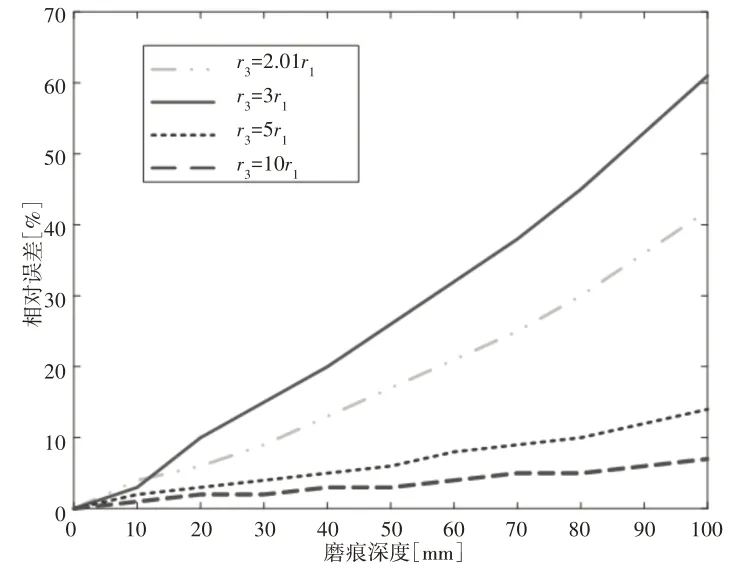
图12 r*相对误差变化规律Fig.12 The Relative Error of r* Versus Wear Scar Depth
J.Warburton认为,当r1=r2时,并且h<r1时=2r3。不断增大将不断减小和呈现相反的发展规律,如图13所示。因此,我们认为引入参与B磨痕的体积计算有所不妥。
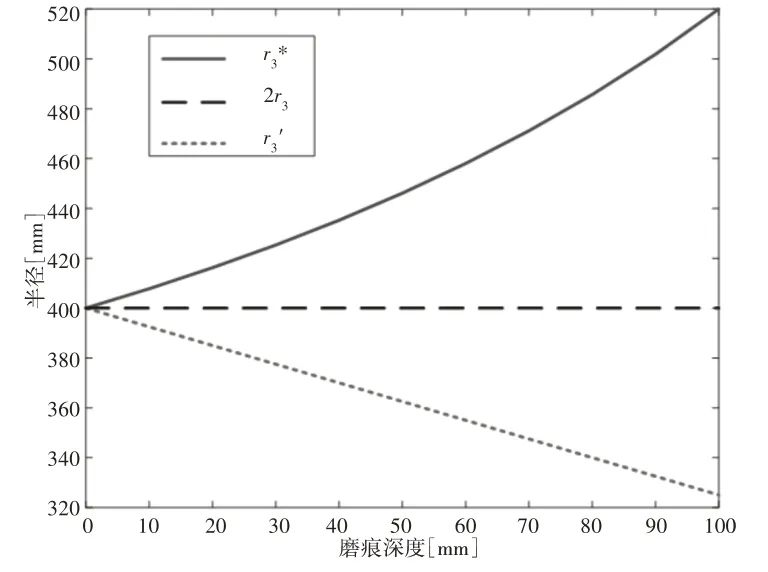
图13 r3*、和r3的变化趋势Fig.13 Trends in r3* and r3 Versus Wear Scar Depth
6 结论
以J.Warburton的研究为基础,主要进行理想磨痕状态下,直线型钢丝接触、直线型钢丝与圆弧型钢丝接触时的磨痕体积计算和误差分析。
直线型钢丝交叉时,无论交叉角度是多少,随着磨痕深度的增大,J.Warburton方法和数值方法所得的磨痕体积均相应增大。J.Warburton方法所得到的磨痕体积始终大于数值方法得到的磨痕体积,是因为J.Warburton 方法所省略的I 项是一个负值。因此,J.Warburton方法关于磨痕体积的计算是把体积放大了。随着磨痕深度的增大,绝对误差和相对误差均增加。当磨痕深度达到2.5mm时,J.Warburton方法带来的误差为0.27%,之后则随着磨痕深度的增大而极具增大,当磨痕深度达到5mm时,J.Warburton方法省略I项所带来的误差为1.43%。因此,当磨痕深度超过钢丝半径的一半时,J.Warburton方法所带来的体积误差将必须予以考虑。
直线型钢丝与圆弧型钢丝接触时,磨痕体积被分为VA和VB两部分,VA可以准确的计算。当拿式(13)来表达VB的体积时,J.Warburton方法总体积计算结果与数值分析相差甚远,最大误差超过10%,同时,反验证得出r*和r3*呈现出截然相反的变化规律,所以r3*参与计算的VB不能反映B磨痕的真实体积。因此,J.Warburton对B磨痕的体积用式(13)来表达持怀疑态度是正确的。分析显示为和呈现相反的发展规律。因此,我们认为引入参与B磨痕的体积计算有所不妥。
本研究为使用J.Warburton方法计算直线型钢丝接触、直线型钢丝与圆弧型钢丝接触时的磨痕体积计算和误差分析提供参考依据。
