基于MFI的不定长CAT选题策略研究

张滨

摘要：针对最大信息量选题策略中因项目曝光不均匀所导致的题库安全性问题，在沿用曝光因子和自动控制区分度函数的基础上，在0-1评分的不定长计算机化自适应测验下提出了一种新的选题策略。蒙特卡洛实验结果表明新的选题策略通过在测验过程中动态控制曝光因子和区分度的大小，使信息量大的项目被选中的概率提高，既保证了测验的效率和精度，同时也较大程度地降低了项目的曝光率，提高了题库的安全性。

关键词：计算机化自适应测验；项目反应理论；选题策略；项目信息量；蒙特卡洛模拟

中图分类号：TP391.76      文献标识码：A

文章编号：1009-3044（2023）31-0071-03

开放科学（资源服务）标识码（OSID）

0 引言

计算机化自适应测验（Computerized Adaptive Test，CAT） 是以现代测量理论为基础，结合了计算机技术的一种新型测验形式。相比传统的测验形式，计算机化自适应测验实现了个性化测验，有着更精确的测量精度并且保证了测验过程更加公平，具有高效、准确、公平、灵活等优势。目前，CAT广泛应用于各类考试中，如国外的美国研究生入学考试（GRE）、美国（工商）管理类研究生入学考试（GMAT） 以及国内的汉语水平测试（HSK）、第四军医大学对应征者进行的文化水平测验都是采用CAT的测验形式。

在计算机化自适应测验中，选题策略是较为关键的一环，不仅直接影响着测验的效率和精度，和题库的安全性也密切相关。目前CAT中用得较多的选题策略是Lord[1]在1970年提出的最大Fisher信息量选题策略（Maximum Fisher Information， MFI） ，该选题策略的测验效率非常高，使用少量的项目就能够快速准确地估计被试的能力水平。然而，MFI对高区分度项目的过度使用使得这些项目的曝光次数较多，低区分度的项目被调用的次数较少，严重影响了题库中项目曝光的均匀性，进而对题库的安全性产生威胁。后来学者们针对MFI在曝光度和安全性上的缺陷提出了不同的选题策略。Chang和Ying提出了按a分层法[2]（a-STR） ，这是一种通过区分度的大小对题库进行分层实现逐层升a的选题策略。针对MFI选题策略的缺陷，结合按a分层法选题策略分层的思想，程小扬和丁树良等引入了三个新的变量提出了引入曝光因子的最大信息量选题策略，下面简称程方法。这三个变量分别是项目j控制曝光因子ecf（j）、ecf（j）的調节因子[λi]以及区分度aj的幂函数a（j，T，k）。其中ecf（j）=mj / m，mj 是项目j被前m-1个被试使用的次数，m是前m-1个被试使用题库中所有项目的平均次数。[a（j，T，k）=a2（T-k）T-1j]，T表示将测验过程中的选题分为T个阶段，k（取值为1，2 ... T） 表示CAT进行选题时项目j所处的阶段[3]。在MFI选题策略基础上引入曝光因子以及区分度函数后，项目的调用次数变得更加均匀，较大程度地改善了项目的曝光率。李萍和甘登文等考虑到引入曝光因子的CAT选题策略仍需对题库进行分层才能够进行选题，提出了不需要进行分层就能自动控制区分度作用的新选题策略[4]，下面简称李方法。通过引入新的区分度幂函数a（j，i）实现在测验过程中动态调节区分度对信息量函数的影响。在定长CAT测验中，a（j，i）=[a2·（test_length-L（i））/test_lengthj]，在不定长CAT测验中，a（j，i）=[a2·（Infor-infor（i））/Inforj]。其中的test_length代表定长测验中预设的测验长度，L（i）是第i个被试当前已经作答完的项目数量，Infor代表不定长测验中被试需完成的项目信息总量，Infor（i）则是第i个被试当前已经完成的项目信息总量。新的区分度幂函数实现了随着测验进程的深入，逐步减少区分度对信息量的影响，在引入曝光因子的基础上，进一步降低了被试的测验长度。朱隆尹、丁树良和程小扬等引入曝光因子后，通过调整信息平均的方法提出了引入曝光因子的平均调整信息选题法[5]。贺翔、罗芬等在动态a分层方法基础上引入均值不等式，构造了新的动态a分层法，进一步提高了测验的安全性[6]。杨文清在引入曝光因子的基础上定义了曝光因子控制指数函数，通过这一函数逐步弱化曝光因子在选题策略中的影响[7]，下面简称杨方法。王璞珏和刘红云基于推荐系统中协同过滤推荐的思想，提出两种可以利用已有答题者数据的CAT选题策略：直接基于答题者推荐（DEBR）和间接基于答题者推荐（IEBR）[8]。李佳和丁树良等提出了区分度与测验进程相匹配的CAT选题策略，这是一种相对严格的升“a”方法[9]。

以上选题策略在对题库安全性控制方面，部分项目仍存在着曝光次数过多的现象。本文在引入曝光因子的基础上，参照李方法的自动控制区分度函数，在选题中同时对区分度和曝光因子进行动态控制，提出了一种新的选题策略，以获得更好的题库安全性。

1 新的选题策略

程方法在MFI选题策略基础上引入曝光因子后，较好地解决了某些项目曝光次数过多的问题，使得项目调用次数更加均匀，但被试的测验长度有所增加。李方法实现了不需要分层即可随着测验过程的深入减小区分度对信息量选题的影响。本文综合了程方法引入曝光因子的后有效降低项目曝光率的优势以及李方法动态控制区分度影响信息量选题方法的特点，参照杨方法在引入曝光因子的同时对曝光因子ecf（j）指数化，杨方法中并未对区分度进行动态调节，而是使用项目本身的区分度去削弱其对信息量的影响。新的选题策略中，通过同时对区分度及曝光因子进行动态调节，削弱曝光因子和区分度在测验后期对信息量的影响，以达到保证测验效率的同时提升题库安全性的目的。

使用新的选题策略项目j要满足的条件为：

[j=argmaxj∈RaIj（θ）ecf（j）t（i）·at（i）j] （1）

式子中的控制曝光因子和区分度的控制函数使用李方法中不定长测验的自动控制区分度函数t（i）=[2（Infor-infor（i））/Infor]，Ra表示当前被试在题库中尚未作答的项目，[Ij（θ）]是估计能力为[θ]的被试在项目j上所含的项目信息量，ecf（j）是程方法中的曝光因子，Infor代表不定长测验中被试需完成的项目信息总量，Infor（i）则是第i个被试当前已经完成的项目信息总量。

2 实验设计

本文实验中的测验采用0-1评分的三参数Logistic模型，其项目反应函数为：

[Pj（θi）=P（uij=1 | θi）=cj+（1-cj）exp{aj（θi-bj）}1+exp{aj（θi-bj）}]  （2）

在3PL模型中，[uij]是取值为0或1的伯努利随机变量，代表着被试i在项目j上的二级计分反应，[uij]值为1表示被试正确作答项目j，[uij]值为0则表示被试错误作答项目j；[Pj（θi）]表示能力为[θ]的被试i在二级评分项目j上正确作答的概率，[aj]，[bj]，[cj]分别为项目j区分度参数，难度系数以及猜测参数。

2.1 模拟生成题库和被试

计算机模拟生成含有项目数量为1 000題的4个题库，题库中项目的区分度参数、难度参数和猜测参数均按照分布模拟生成[9]。得到以下4个项目参数服从不同分布的题库：

题库1生成区分度a服从对数正态分布，难度b服从标准正态分布，猜测参数c服从α为5，β为17的贝塔分布，记为[Ina～N（0，1）∧a∈（0.2，2.5），b～N（0，1）∧b∈（-3，3），c～Beta（5，17）]。

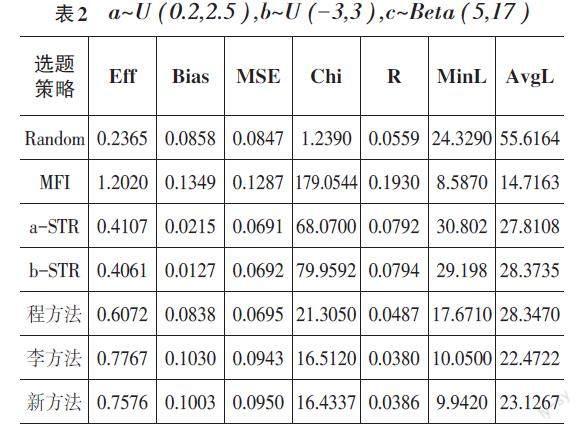
题库2生成区分度a服从均匀分布，难度b服从均匀分布，猜测参数c服从α为5，β为17的贝塔分布，记为[a～U（0.2，2.5），b～U（-3，3），c～Beta（5，17）]。

题库3生成区分度a服从对数正态分布，难度b服从均匀分布，猜测参数服从α为5，β为17的贝塔分布，记为[Ina～N（0，1）∧a∈（0.2，2.5），b～U（-3，3），c～Beta（5，17）]。

题库4生成区分度a服从均匀分布，难度b服从标准正态分布，猜测参数服从α为5，β为17的贝塔分布，记为[a～U（0.2，2.5），b～N（0，1）∧b∈（-3，3），c～Beta（5，17）]。

计算机模拟生成1 000个被试，被试的能力参数均服从标准正态分布，即能力参数[θ～N（0，1）]，且[-3<θ<3]。

2.2 模拟被试作答

根据所选项目j的项目参数a、b、c以及被试i的能力估计值θ，代入式（2）计算其答对项目的概率[Pj（θi）]，同时通过计算机模拟生成一个服从0到1之间均匀分布的随机数r，记为[r～U（0，1）]。如果[r<Pj（θi）]，认为被试i正确作答了项目j，记被试i在项目j上作答反应[uij=1]；倘若[r⩾Pj（θi）]，则认为被试i错误作答了项目j，则被试i在项目j上作答反应[uij=0]。

2.3 模拟CAT施测过程

CAT施测过程有两个阶段，第一阶段是模拟测试的初始阶段，从题库中随机选择3个项目供被试作答，答对计1分，答错计0分，计算被试的得分与失分的比值的自然对数值，将其作为被试的初始能力估计值；随后进入第二阶段，即被试能力的精确估计阶段，使用贝叶斯期望后验估计方法精准估计被试的能力值。

2.4 评价指标

本文用测验效率Eff、测验偏差Bias、测验标准误差MSE、试题曝光均匀度Chi及测验重叠率R、最小测验试题长度MinL、平均测验试题长度AvgL等评价指标来评价选题策略的优劣，除测验效率值为越大越好以外，其余评价指标均为越小越好。

3 实验结果及其分析

表1至表4的数据是在不定长CAT测验中选用三参数Logistic模型的实验结果，通过四张表数据可以看出，新的选题策略在保证测验效率和测量精度的情况下，有效降低了测验的曝光均匀度，保证了题库的安全性。在测验效率上，新方法除略低于李方法外，比其他方法都表现得更好；新方法在损失少许测量精度的同时，极大地降低了测验项目的曝光率和测验的重叠率；新方法在测验长度上总体与李方法相当，优于其他的选题策略。总体而言，新的选题策略提高了题库的安全性的同时，测量的精度依然能够保持在一个较好的水平。

4 小结与展望

本文对CAT的重要组成部分选题策略进行了研究。在选题策略的研究中，沿用程小扬提出的曝光因子和李萍的自动控制区分度函数的基础上，在使用0-1评分三参数logistic模型的不定长CAT中，提出了新的选题策略。Monte Carlo模拟实验表明新的选题策略在保证测量精度的同时，大幅度地降低了项目的曝光均匀度，有效提升了题库的安全性。在自适应测验选题算法改进上，新的选题策略较以往的选题方法在曝光均匀度上表现更好，但在测验效率和测量精度等指标的表现上没有与李方法拉开差距。因此，在今后的研究中可以进一步提高该选题策略的测验精度，降低其测验的长度；其次，新的选题策略仅在不定长CAT上进行了应用，其在定长CAT上的表现还需进一步的研究。

参考文献：

[1] LORD F M. Some test theory for tailored testing[R]// HOLZMAN W H.Computer assisted instruction， testing， and guidance.New York： Harper & Row， 1970：139-183.

[2] CHANG H H，YING Z L. A-stratified multistage computerized adaptive testing， Applied Psychological Measurement， 1999， 23（3）： 211-222.

[3] 程小扬，丁树良，严深海，等.引入曝光因子的计算机化自适应测验选题策略[J].心理学报，2011，43（2）：203-212.

[4] 李萍，甘登文，丁树良.自动控制区分度作用的选题策略研究[J].江西师范大学学报（自然科学版），2013，37（1）：101-105.

[5] 朱隆尹，丁树良，程小扬，等.不定长CAT引入曝光因子的平均调整信息选题策略研究[J].心理学探新，2015，35（1）：68-71.

[6] 贺翔，罗芬，甘登文，等.一种提升题库安全性的选题策略[J].江西师范大学学报（自然科学版），2016，40（4）：363-368.

[7] 杨文清.CAT中提升题库安全性的选题策略和a分层终止规则的研究[D].南昌：江西师范大学，2017.

[8] 王璞珏，刘红云.让自适应测验更知人善选——基于推荐系统的选题策略[J].心理学报，2019，51（9）：1057-1067.

[9] 李佳，丁树良，况天昊.区分度与测验进程相匹配的CAT选题策略[J].江西师范大学学报（自然科学版），2021，45（4）：384-389.

【通联编辑：王 力】