纳米银球附近三能级原子的自发辐射动力学特性*
2023-12-22高广波单馨雨黄勇刚
李 芸,高广波,单馨雨,黄勇刚
(吉首大学物理与机电工程学院,湖南 吉首 416000)
等离激元自Kronig和Pines提出后就备受关注[1-2].1957年,Ritchie通过研究快速电子穿过光学厚金属膜时的能量损失特性,预测了金属表面存在自由电子的集体振荡[3],进而提出了表面等离激元的概念.1968年,Ritchie将Wood发现的金属光栅异常现象[4]归因于表面等离激元共振[5].1970年,Kreibig运用表面等离激元的概念研究了金属纳米颗粒的光学性质[6].表面等离激元是金属中自由电子和电磁场相互作用、共谐振荡形成的电磁模式,可以将电磁场约束在金属表面附近的纳米尺度范围内[7],具有极大的局域场增强效应,因而引起了广大学者的研究兴趣[8-15].
表面等离激元不仅可以改变光子局域态密度,还可以调控附近原子的自发辐射[16-18].例如,赵运进等[17]研究发现,当二能级原子位于纳米球表面或金属板上方2 nm时,其自发辐射增强因子可超过105.田锰[18]探究了纳米球附近二能级原子的非马尔科夫自发辐射动力学特性,结果显示,不同尺寸的金属纳米柱中表面等离激元对自发辐射的调控作用明显不同,当纳米柱的高度变低时,峰值频率急剧蓝移,当纳米柱半径减小时,峰值频率急剧红移.此外,二能级原子和表面等离激元的相干相互作用可以形成束缚态,此时,处于激发态的原子不会完全衰减到基态,而是演化到束缚态上[19].不同于二能级原子,V型三能级原子存在2个跃迁通道,其自发辐射动力学可能呈现出量子干涉效应.因此,探究纳米银球附近三能级原子的自发辐射动力学具有重要意义.笔者拟采用格林函数预解算子方法,探讨原子跃迁频率及原子-纳米银球表面距离对V型三能级原子的自发辐射动力学影响,并在此基础上,研究纳米银球附近V型三能级原子的自发辐射动力学特性.
1 模型与理论

图1 模型示意Fig. 1 Model Representation
三能级系统模型如图1所示.V型三能级原子位于纳米银球附近,2个上能级为|a1〉,|a2〉,下能级为基态|g〉,纳米银球的半径R=20 nm.原子和纳米银球均置于真空中,真空中相对介电函数ε1=1,银的介电函数为ε2.
在高频时,除了自由电子响应外,壳层电子也会对电磁场产生强烈的响应[20-21],通常采用Drude-Lorentz模型进行描述[20]:

设V型三能级原子的2个上能级|a1〉和|a2〉均可向基态|g〉跃迁.在偶极近似和旋波近似下,系统的Hamiltonian可表达为[22]
H=H0+H1.
其中:H0为非相互作用部分,
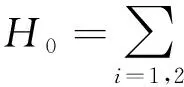
H1为相互作用部分,
这里ωi为上能级|ai〉到基态|g〉的跃迁频率,di为对应的跃迁偶极矩阵元.
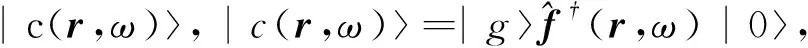
其中t时刻系统处于|aj,0〉态的几率幅可由时间演化算符U(t)的矩阵元表示,即
cj(t)=〈aj,0|U(t)|a1,0〉.
(1)
由推迟和超前格林函数可知,时间演化算符
(2)
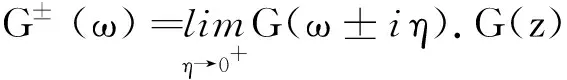
利用投影算符技术,格林函数矩阵元Gij(z)=〈ai,0|G(z)|aj,0〉(i,j=1,2),满足
(3)
其中
(4)
这里
Γij(z)=2πIm(gij(z)θ(z)),
gij(z)可用光子并矢格林函数G(r0,r0,ω)表达,即

对于纳米银球,光子并矢格林函数G(r0,r0,ω)可通过半解析方法获得,详细可参考文献[23-24].
解方程组(3),可得
其中F1=ω-ω1-R11(ω) ,F2=ω-ω2-R22(ω).将G11(ω)和G21(ω)代入(1),(2)式,可得
(5)
其中动力学演化谱
(6)
2 结果
2.1 原子跃迁频率对自发辐射动力学的影响
首先研究不同跃迁频率对三能级原子自发辐射动力学的影响.为了简单,不特别说明的情况下,设V型原子的2个跃迁通道均具有平行的跃迁偶极矩,方向均沿着x方向,大小分别为d1=24 D,d2=26 D,原子离纳米银球表面距离h=1 nm.由(5),(6)式可知,激发态几率幅随时间的演化可由动力学演化谱得到.为此,笔者计算了不同跃迁频率下的Γij(ω)和Δij(ω),结果如图2所示.
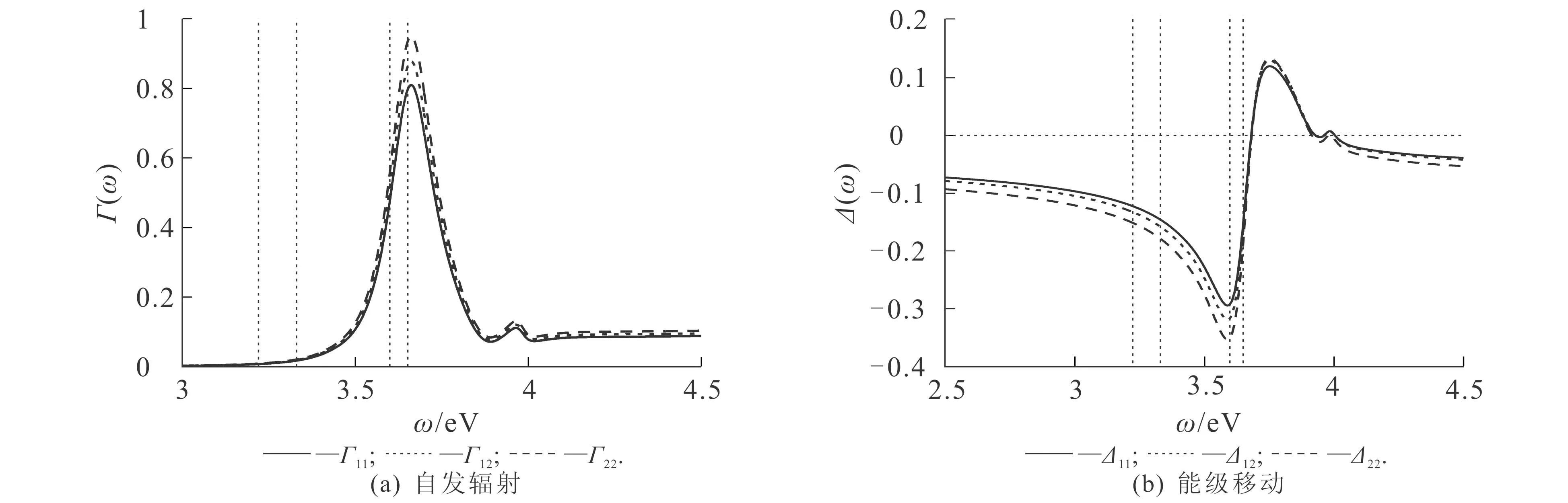
图2 原子-纳米银球距离为1 nm时原子的自发辐射和能级移动Fig. 2 Spontaneous Radiation and Energy Level Shift of Atoms at 11 nm Atom-Nanosphere Distance
从图2(a)可知,Γ22(ω)稍大于Γ11(ω),且Γ12(ω)处于Γ22(ω)和Γ11(ω)之间.这主要是因为,当偶极矩平行时,Γij(ω)∝didj,d2(26 D)稍大于d1(24 D).此外,图2(a)中,Γij(ω)(i,j=1,2)均在ω=3.652 eV附近取极大值,这主要是纳米银球中表面等离激元共振模式的贡献.从图2(b)可知,在Γij(ω)的峰值附近,Δij(ω)发生急剧变化,远离峰值后,Δij(ω)随频率缓慢变化,这主要是由于Δij(ω)是Γij(ω)的希尔伯特变换.从图2(b)还可知,对于不同i和j,Δij(ω)∝didj,Δij(ω)与y=0具有相同的交点,在交点以外,有|Δ11(ω)|<|Δ12(ω)|<|Δ22(ω)|.
接下来,研究原子跃迁频率分别远离和靠近Γij(ω)峰值频率时的自发辐射动力学特性.当原子的2个跃迁频率均远离Γij(ω)峰值频率时,即ω1=3.33 eV和ω2=3.22 eV时,原子的演化谱和动力学结果如图3所示.
从图3(a)可知,动力学演化谱S1(ω)和S2(ω)均呈现出明显的双峰结构,不同的是,S1(ω)的2个峰值均为正值,而S2(ω)的2个峰值为一正一负.这主要是由于初始系统处于|a1态,即t=0时,由(5)式可知,演化谱S1(ω)的积分为1,而S2(ω)的积分为0.
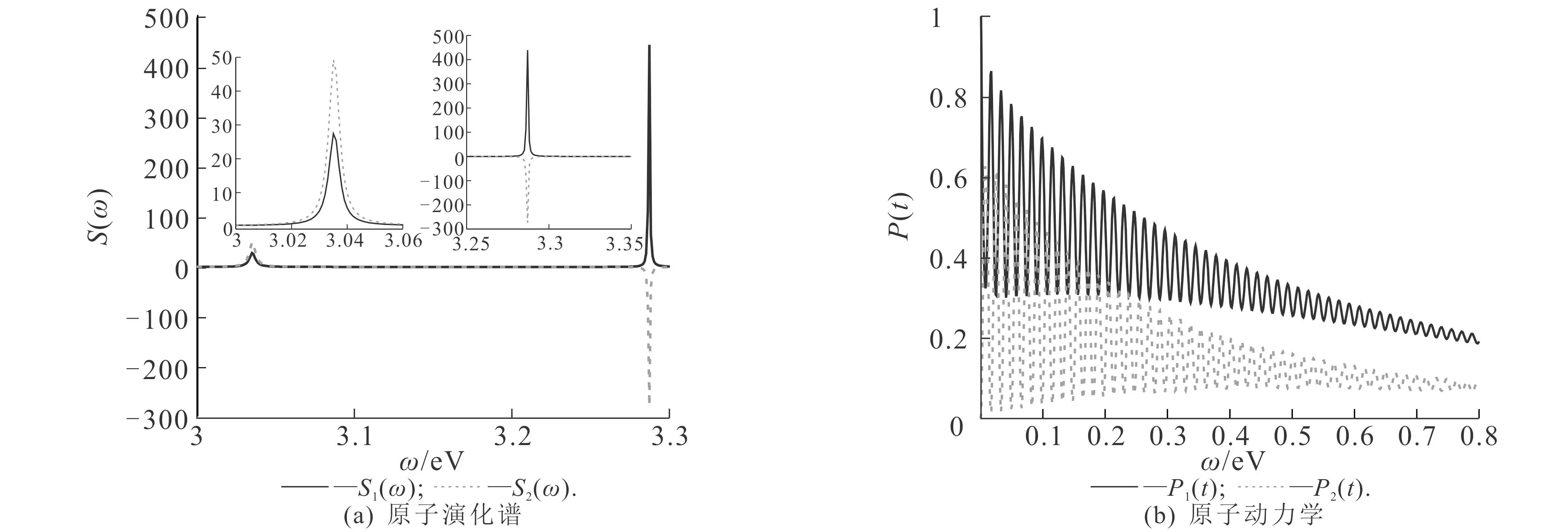
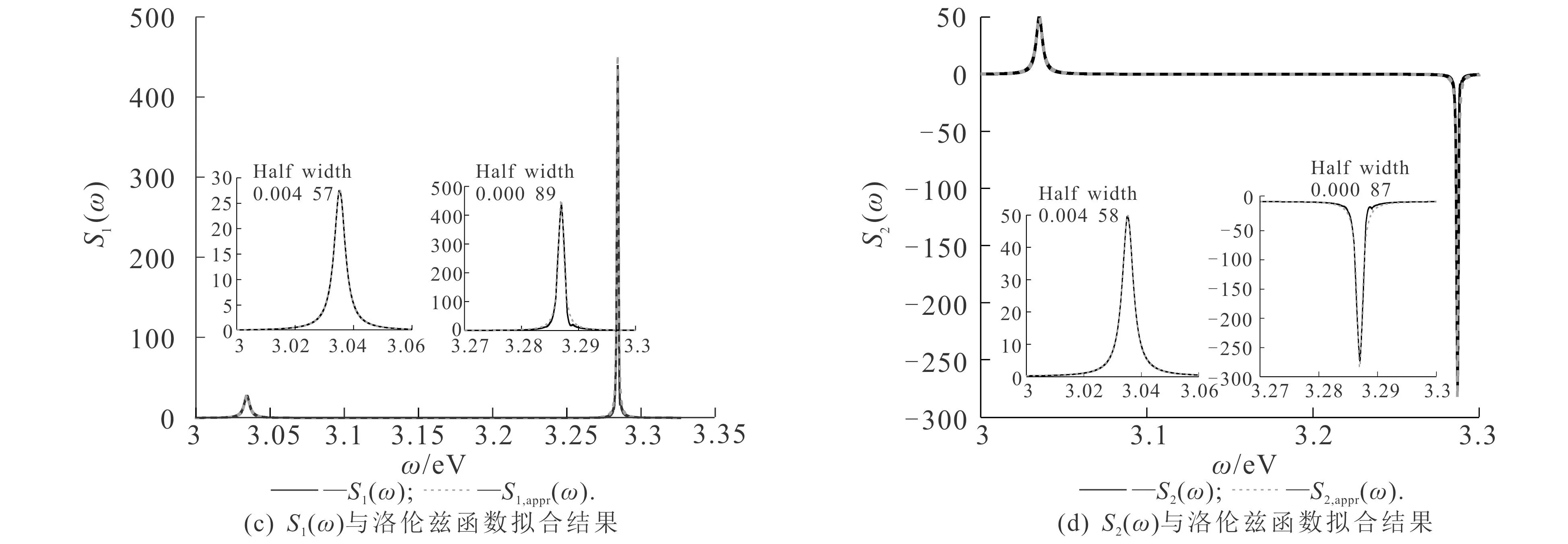

图3 原子的演化谱和动力学及用洛伦兹函数拟合后的结果(ω1=3.33 eV,ω2=3.22 eV)Fig. 3 Evolution Spectrum and Dynamics of Atoms and Results After Fitting with Lorentz Function
从图3(b)可知:t时刻,系统仍然处于|a1态的几率幅P1(t)随时间的增加边振荡边衰减,呈现出明显的衰减拉比振荡特征;处于|a2态的几率幅P2(t)由初始的0逐渐增大到峰值(0.7左右)后,也发生衰减拉比振荡.
为了理解P1(t)和P2(t)的动力学特性,采用双洛伦兹函数拟合S1(ω)和S2(ω),即
由图3(c),(d)可知,Si(ω)均能用2个洛伦兹函数完美拟合.拟合函数分别为
将S1,appr(ω)代入(5)式,并利用洛伦兹函数性质,可得
(7)
由(7)式可知,|a1态的几率幅除了随时间指数衰减外,还以频率ω12-ω11随时间振荡.从图3(e)可知,|a1态几率幅的数值解与近似解拟合较好.类似地,从图3(f)可知,|a2态几率幅的数值解与近似解也拟合较好.由(7)式可知,当|ω12-ω11|≫(γ11+γ12)时,即振荡频率远大于衰减率时,原子处于|a1态的几率幅随着时间的变化为衰减拉比振荡,并呈现出明显的非马尔科夫特性.
物理上,初始处于|a1态的原子,在t时刻仍然处于|a1态可通过2种方式实现.第1种路径为|a1→|g→|a1,即原子首先从|a1态跃迁到基态|g辐射光子,随后吸收该光子从基态|g跃迁到|a1态;第2种路径为|a1→|g→|a2→|g→|a1,即原子从|a1态跃迁到基态|g辐射光子,随后吸收光子跃迁到|a2态,再辐射光子回到基态|g,最后吸收光子跃迁到|a1态.因此,系统存在2种不同的跃迁通道,可能呈现出明显的干涉效应.
当原子的2个跃迁频率靠近峰值频率时,即ω1=3.6 eV和ω2=3.652 eV时,原子的演化谱和动力学结果如图4所示.
从图4(a)可知,类似于图3(a),S1(ω)和S2(ω)也呈现出明显的双峰结构,S1(ω)的2个峰值均为正值,而S2(ω)的2个峰值为一正一负.不同的是,与图3(a)相比,图4(a)的峰值较小,尤其是低频处的峰值.
从图4(b)可知:t时刻,系统仍然处于|a1态的几率幅P1(t)随着时间的增加也边振荡边衰减,但很快就变为指数衰减而无振荡特征;处于|a2态的几率幅P2(t)也出现类似的动力学特性.
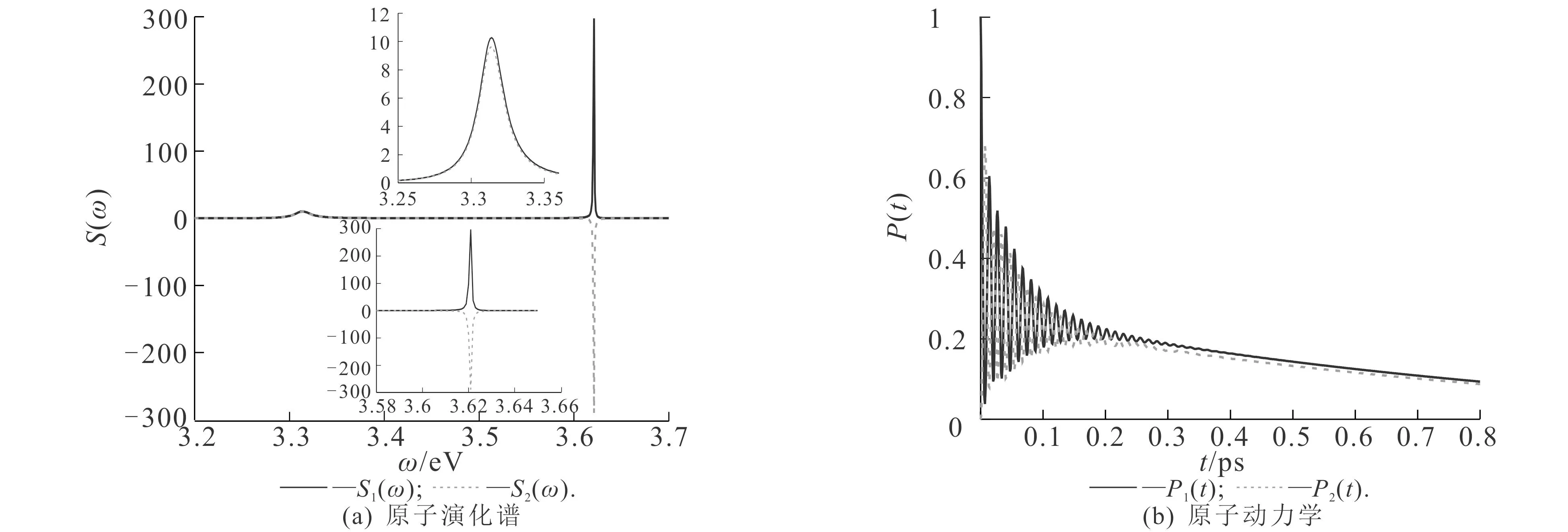

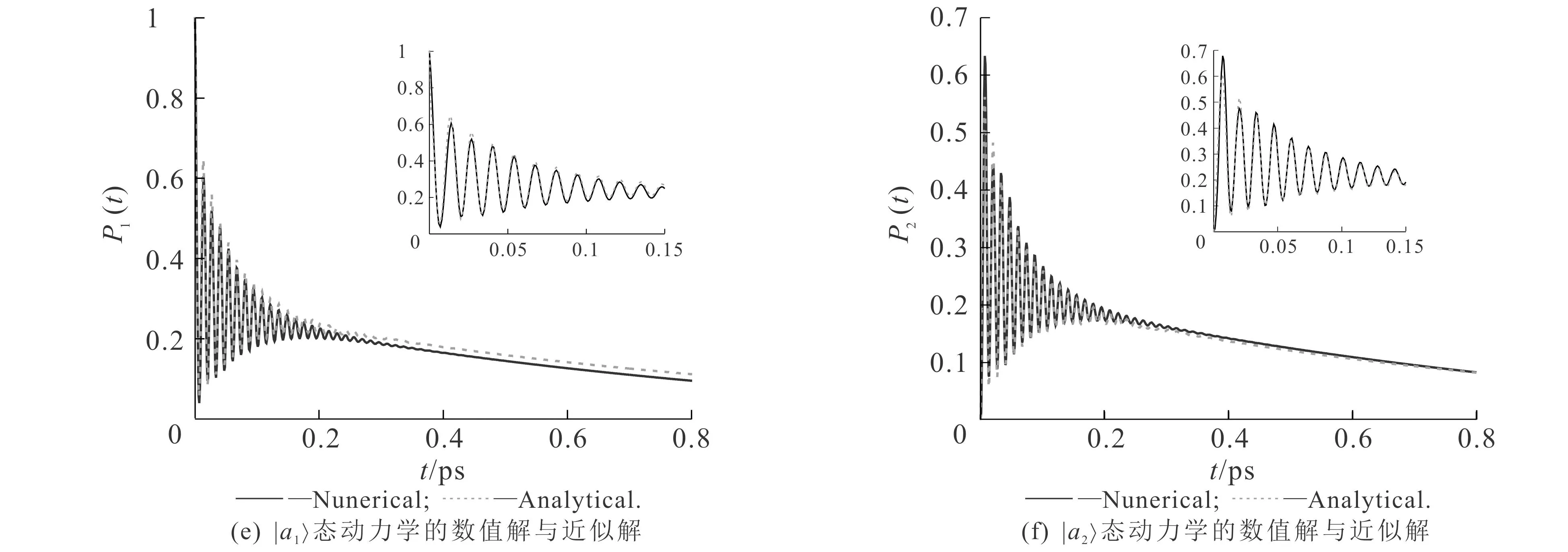
图4 原子的演化谱和动力学及用洛伦兹函数拟合后的结果(ω1=3.6 eV,ω2=3.652 eV)Fig. 4 Evolution Spectrum and Dynamics of Atoms and Results Fitted with Lorentz Function
为了进一步理解P1(t)和P2(t)随时间的演化特征,也采用双洛伦兹函数分别拟合S1(ω)和S2(ω),得到
拟合结果如图4(c),(d)所示.图4(c)中,拟合结果S1,appr(ω)与精确解S1(ω)几乎完美重合.类似地,图4(d)中,拟合结果S2,appr(ω)与精确解S2(ω)也重合较好.从图4(e),(f)可知,|a1态和|a2态原子的动力学数值解与近似解均拟合较好.

2.2 原子-纳米银球表面距离对自发辐射动力学的影响
2.1节中,笔者研究了距离为1 nm时的V型三能级原子动力学特性,本节中,距离增大到2 nm,V型三能级原子的2个跃迁频率仍然取ω1=3.6 eV和ω2=3.652 eV.
当原子-纳米银球表面距离为2 nm时,原子的自发辐射和能级移动结果如图5所示.

图5 原子-纳米银球距离为2 nm时原子的自发辐射和能级移动Fig. 5 Spontaneous Radiation and Energy Level Shift of Atoms at 2 nm Atom-Nanosphere Distance
从图5可知,相较于距离为1 nm时的结果,距离为2 nm时,自发辐射增强谱的峰值和能级移动的峰值均急剧降低,且均降低为1 nm时的1/8左右.
当原子-纳米银球表面距离为2 nm时,原子的演化谱和动力学结果如图6所示.
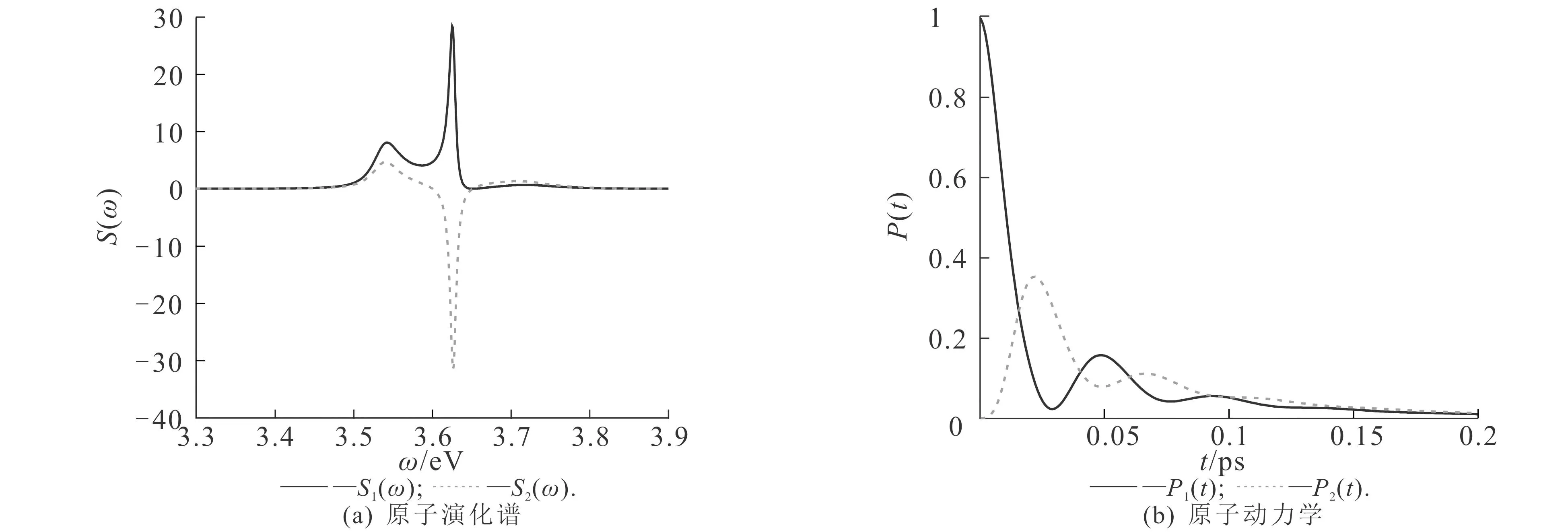
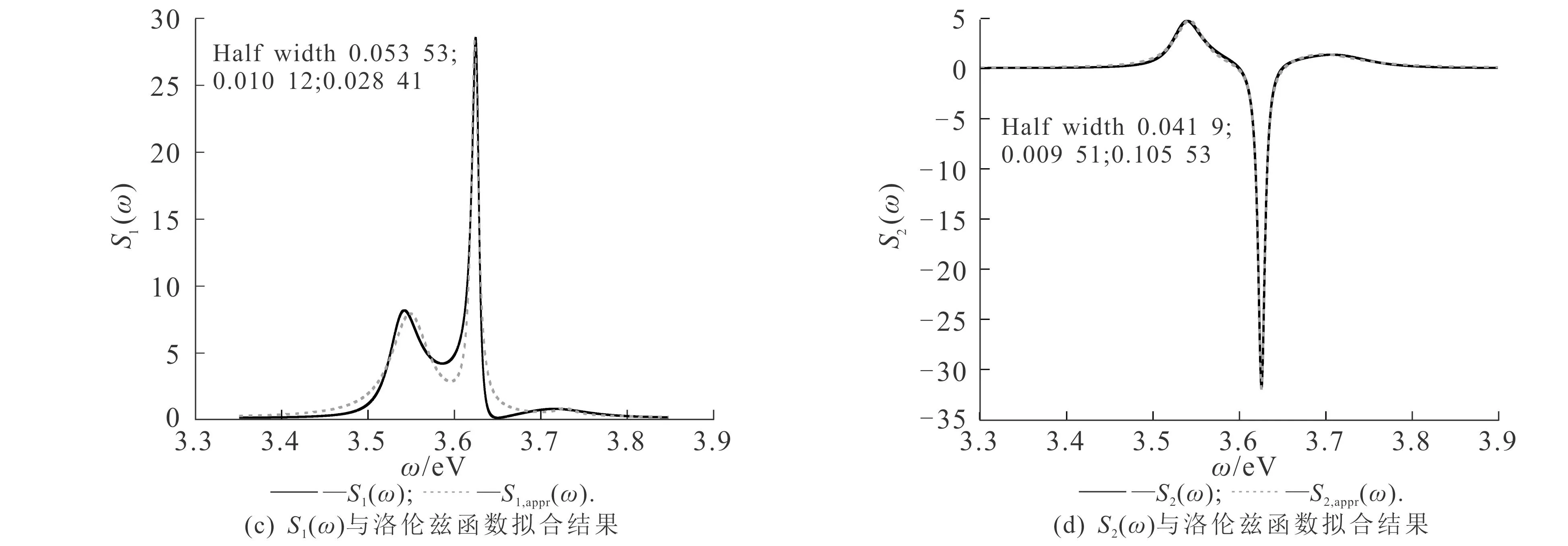
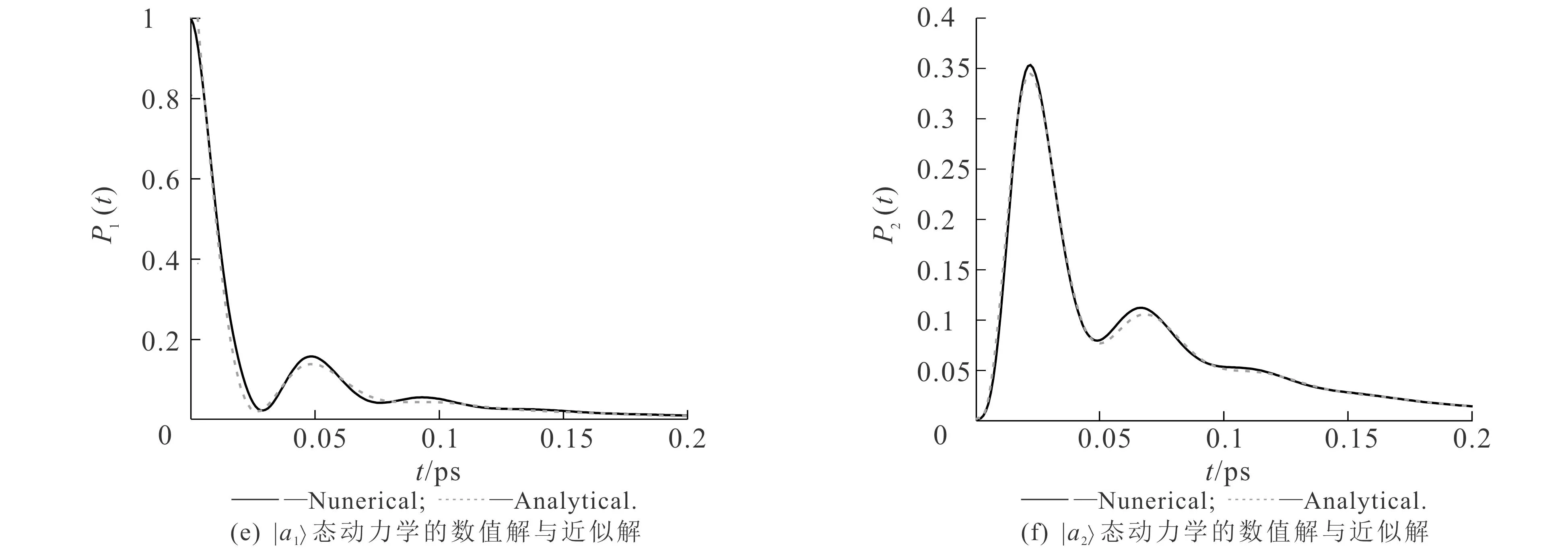
图6 原子-纳米银球表面距离为2 nm时原子的演化谱和动力学及用洛伦兹函数拟合后的结果Fig. 6 Evolution Spectrum and Dynamics of Atoms at 2 nm Atom-Nanospere Distance and Results Fitted with Lorentz Function
从图6(a)可知,自发辐射动力学演化谱S1(ω)和S2(ω)的2个主峰之间距离较近,且在2个主峰的左边均存在1个次要的峰.这一特征不同于图4(a)中距离为1 nm时的双峰结果.
从图6(b)可知,|a1态的几率幅P1(t)和|a2态的几率幅P2(t)随着时间的增加也呈现出衰减拉比振荡特征.与距离为1 nm时的结果相比,距离为2 nm时的振荡频率较低,衰减较快.
为了理解上述动力学特征,采用3个洛伦兹函数的和来拟合S1(ω)和S2(ω),即
最终得到拟合参数如下:对于S1,A11=0.649 7,ω11=3.548 9,γ11=0.053 5,A12=0.437 0,ω12=3.624 3,γ12=0.010 1,A13=0.022 4,ω13=3.730 1,γ13=0.028 4;对于S2,A21=0.307 4,ω21=3.542 6,γ21=0.041 9,A22=-0.487 0,ω22=3.626 2,γ22=0.009 5,A23=-0.238 0,ω23=3.694 9,γ23=0.105 5.
从图6(c),(d)可知,进行洛伦兹函数拟合后,S1(ω),S2(ω)的数值解与近似解稍有差别.
对于动力学,近似演化谱给出的激发态|ai的几率幅
(8)
从图6(e),(f)可知,|a1态几率幅、|a2态几率幅的数值解与近似解均拟合较好.
(8)式为读者理解动力学的缓慢振荡和快速衰减特征提供了重要依据.例如,对于S1(ω),拟合参数A13远小于A11和A12,表明中心频率为ω11和ω12的2个主峰对谱的贡献较大.相较于距离为1 nm时的结果,距离为2 nm时的|ω11-ω12|较小,导致振荡频率较低,且距离为2 nm时的半高宽(γ11=0.053 55 eV,γ12=0.010 12 eV)较大,导致衰减较快.
3 结论
笔者采用格林函数预解算子方法,研究了纳米银球附近V型三能级原子的自发辐射动力学特性.初始处于激发态|a1的原子有2个可能的跃迁通道回到|a1态,分别是|a1→|g→|a1和|a1→|g→|a2→|g→|a1,系统动力学呈现出明显的量子干涉效应.原子的跃迁频率和原子到纳米银球表面的距离,对V型三能级原子的自发辐射动力学具有重要的影响.动力学演化谱均呈现出2个主峰,且高频峰的宽度远远小于低频峰的宽度,随着距离的增大,2个主峰之间的频率差减小,当跃迁频率接近等离激元共振频率时,原子的演化谱峰值降低,尤其是低频峰.此外,笔者采用多个洛伦兹函数的和拟合了动力学演化谱,解释了动力学边振荡边衰减的特征,并证明了振荡频率由演化谱峰值频率差决定,而衰减的快慢主要由演化谱的2个主峰宽度决定.
