石墨烯可调谐双频完美吸收器设计*
2023-12-22赵金云单馨雨高广波黄勇刚
赵金云,单馨雨,高广波,黄勇刚
(吉首大学物理与机电工程学院,湖南 吉首 416000)
超材料(Metamaterials,MTM)是由微纳结构周期排布构成的人工复合材料,电磁MTM具有天然材料所不具备的超常物理性质,如负介电常数、负磁导率等[1-3].基于这些特性,科学家将MTM用于操纵电磁波,使得MTM在太赫兹传感和光吸收等多个研究领域[4-9]得到广泛应用.其中,MTM吸收器因具有广泛的应用前景而备受关注[10-12].传统的MTM吸收器由金属、介质材料和金属3层结构组成[10-12],吸收率达到90%以上.随着研究的深入,科学家成功设计出多种由不同材料和不同结构组成的太赫兹双频窄带吸收器.譬如:Pan等[13]设计了一种由金组成的风车形结构的太赫兹吸收器,该吸收器在0.371 THz和0.464 THz处的吸收率分别为99.8%和99.2%,相对半峰全宽分别为0.76%和0.31%,吸收器在2个共振频率处实现完美吸收,具有较高的品质因子(Q),然而该吸收器一旦制作完成,其共振频率就难以调节;Kang等[14]设计了一种由金方环-钛酸锶-金层组成的可调双波段超材料吸收器,其吸收共振频率可通过温度进行调控,室温下该吸收器在0.162 THz和0.329 THz处的吸收率都超过99%,但2个共振频率过于接近且可调范围相对较窄;Luo等[15]设计了一种由InSb组成的圆盘-同心环吸收器,该吸收器在1.598 THz和1.926 THz处的吸收率分别高达99.4%和98.7%,吸收峰位可以通过温度进行微调,但品质因子较低,分别为35.51和23.78.石墨烯具有优异的光学性能,其介电函数可以通过化学势进一步调节.利用这一性质,Liu等[16]设计了一种双波段太赫兹完美吸收器,该吸收器在4.13 THz和4.38 THz处实现了完美吸收,然而受制于该吸收器的几何结构,其吸收峰位仅可微调;Chen等[17]设计了一种由石墨烯-介质-金属组成的可调超材料吸收器,该吸收器在3.74 THz和7.73 THz频率处的吸收率均超过99.8%,品质因子也较高,分别为97.88和216.29,此外,该吸收器的吸收峰位可通过石墨烯化学势进行大幅度调节,因而在太赫兹吸收和传感领域具有潜在应用价值.笔者拟利用石墨烯优异的可调光学特性,设计一种由石墨烯谐振器、SiO2介质层及金属反射层组成的可调谐双频完美吸收器,并系统研究偏振角、石墨烯化学势及器件几何尺寸对吸收器吸收性能的影响,进一步解释吸收器吸收的原理.
1 设计结构和模拟方法
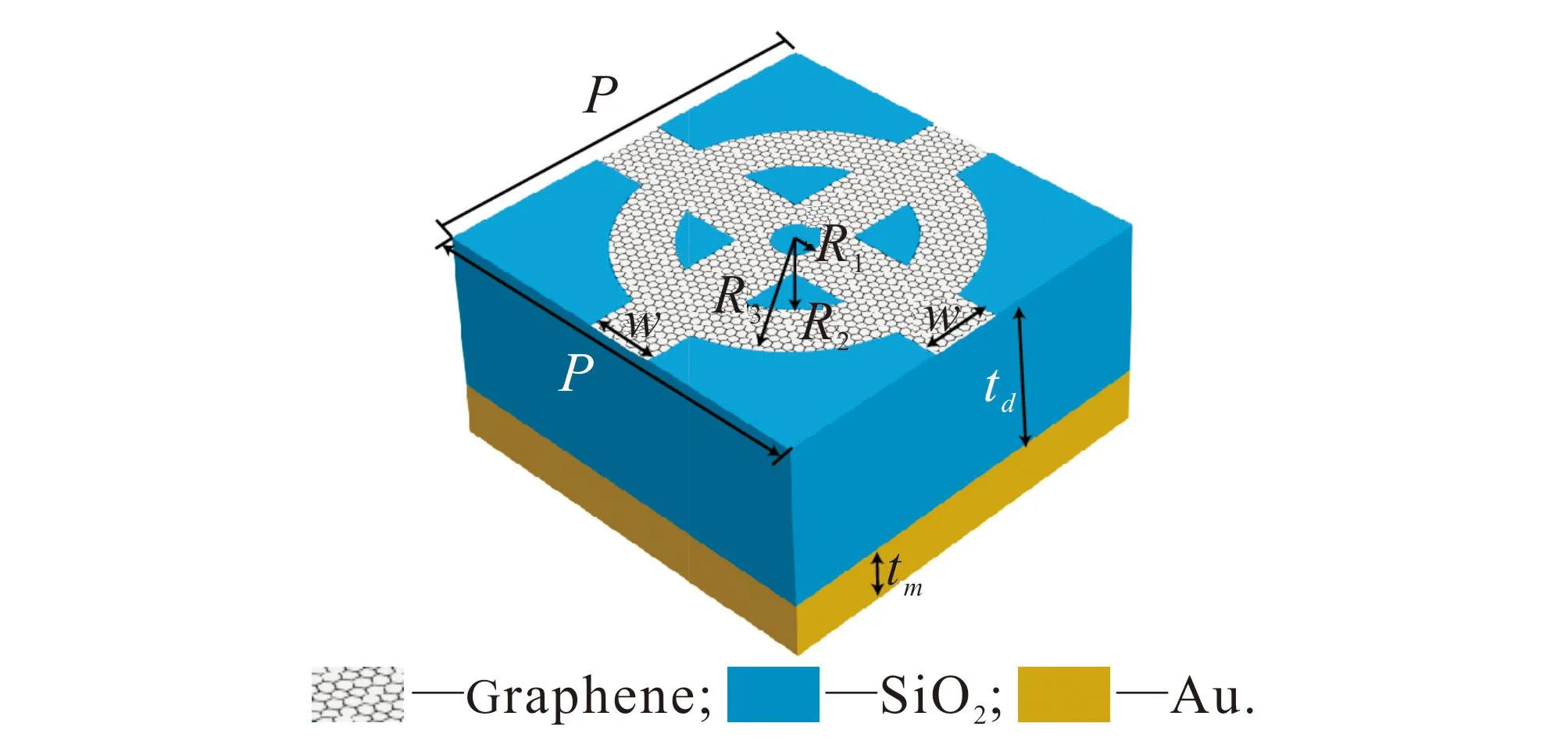
图1 吸收器3D结构Fig. 1 3D Structure of the Absorber
吸收器的单元晶胞结构如图1所示.从图1可知,图案化石墨烯沉积在SiO2介质上,衬底用金镜阻挡太赫兹波传输.SiO2介质的厚度(td)为3.0 μm,Au的厚度(tm)为0.37 μm,金镜的电导率(σ)为4.56×107S/m[18],介质层材料SiO2的介电常数εr为2.25[19].设P为晶胞的周期,W为条形石墨烯的宽度,R1,R2和R3为环的半径.吸收器的优化结构参数设置如下:P=2.8 μm,W=0.32 μm,R1=0.25 μm,R2=0.67 μm,R3=1 μm.
石墨烯电导率可以用经典的Kubo公式[20]计算:
σgra=σintra+σinter,
(1)
其中
这里:ω代表角频率;τ代表弛豫时间;T代表温度;e代表电子电量;KB代表玻尔兹曼常数;ћ代表约化普朗克常数;μc代表石墨烯的化学势.
本研究中,设环境温度T为300 K,此时,μc≫kBT,在太赫兹范围内,石墨烯的带间跃迁对电导率贡献较小,带内跃迁起主要作用.因此,(1)式可以简化为[17]
(2)
其中弛豫时间τ=9 ps.由(2)式可知,石墨烯电导率σgra主要取决于角频率ω和化学势μc,可以通过调节偏压或者化学掺杂进行控制.单层石墨烯等效介电常数可表达为[17]
其中:ε0代表真空中的介电常数;tg代表石墨烯厚度,tg=1 nm[17].
吸收器金反射镜的厚度远大于趋肤深度,电磁波无法透射.基于CMT,系统的吸收率[21]
(3)
其中:ω0代表共振频率;δ代表器件的固有损耗;γ代表器件的外部泄漏率.由(3)式可知,当外部泄漏率和固有本征损失率相同(γ=δ),且频率等于共振频率(ω=ω0)时,系统达到完美吸收,这一现象称作临界耦合.
笔者采用COMSOL Multiphysics软件进行数值仿真.平面波入射下,在x和y方向上均采用周期边界条件,z方向上采用开放边界条件,先计算反射率(R),再计算吸收率(A):A=1-R.
2 结果
当μc= 0.4 eV,电磁波垂直入射时,TE模式电磁波的透射、反射和吸收光谱如图2所示.由图2可知:吸收器的透射率几乎为0,说明金层厚度远超趋肤深度,几乎没有电磁波可以穿透金层;在6.363 THz和8.987 THz处,吸收器的吸收光谱出现了2个高吸收峰,吸收率分别为99.98%和99.99%,相应的反射率几乎为0.为了方便区分,将6.363 THz和8.987 THz分别用M0模式和M1模式表示.
临界耦合情况下,数值模拟和CMT拟合的吸收光谱如图3所示.从图3可知,CMT拟合的吸收光谱与数值模拟的吸收光谱拟合度较高.根据CMT,M0模式和M1模式在临界耦合情况下的损失率分别为δ0=γ0=0.008 89 THz和δ1=γ1=0.008 88 THz,品质因子分别为QCMT0=178.94和QCMT1=253.12,与数值模拟所取得的品质因子(分别为Q0= 187.15和Q1= 256.77)非常接近.以上结果说明,吸收器的完美吸收主要来源于临界耦合[22].
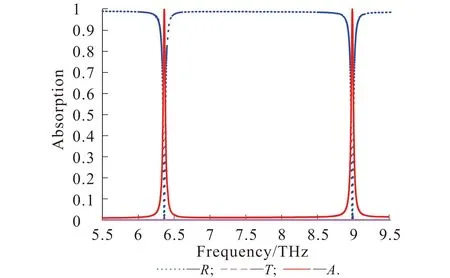
图2 垂直入射时吸收器的反射、透射、吸收光谱Fig. 2 Reflectance,Transmission and Absorption Spectra of the Absorber at the Vertical Incidence

图3 数值模拟及CMT拟合的吸收光谱Fig. 3 Numerical Simulation with CMT Fitted Absorption Spectra
偏振角对MTM吸收器吸收特性的影响如图3所示.

图4 偏振角对吸收率的影响Fig. 4 Effect of Polarization Angle on Absorbance
吸收器具有C4对称性,故仅需考虑0°~45°范围内的偏振角.图4(a)展示了φ=0°和φ=45°时的吸收光谱,可以看出,在2个偏振角下,吸收器的吸收曲线几乎相同,均能实现完美吸收.由图4(b)可知,当φ从0°增加至80°时,吸收光谱的峰位无明显变化,吸收器仍能保持完美吸收特性.这些结果说明,MTM吸收器对偏振角有很强的鲁棒性.
石墨烯化学势对吸收器的共振频率、吸收率及品质因子的影响如图5所示.
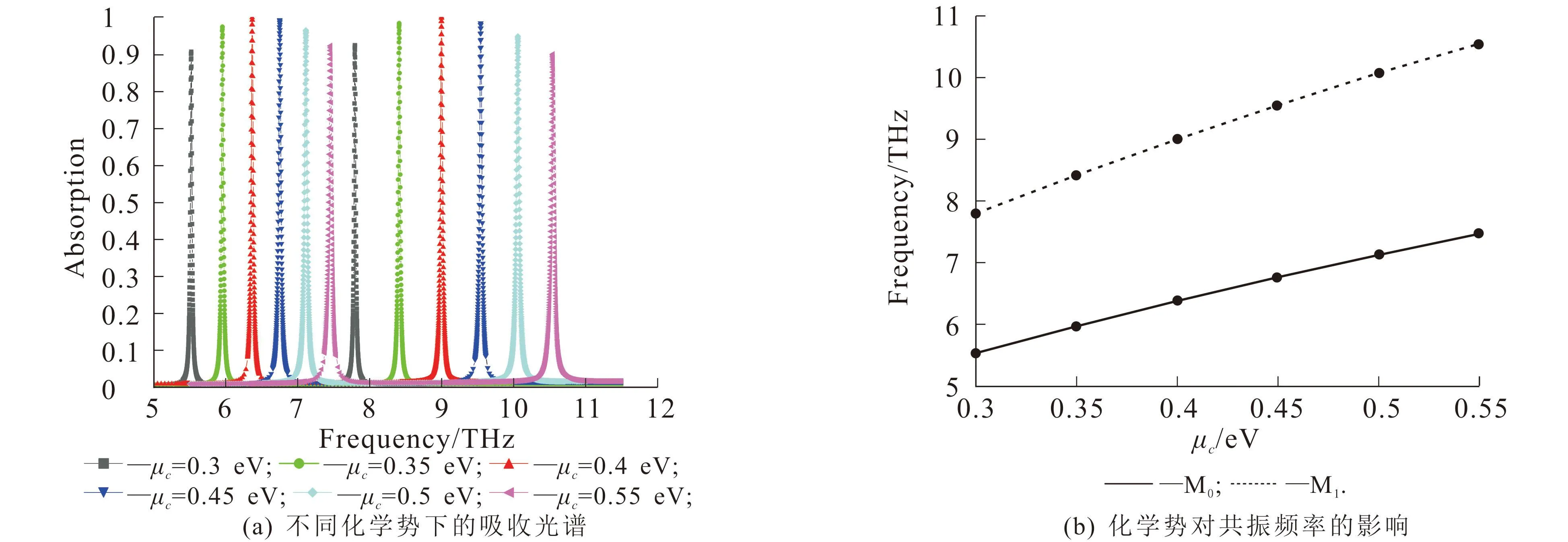
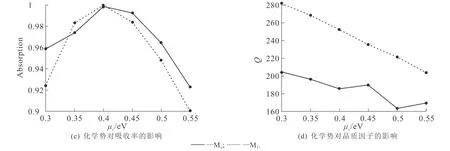
图5 化学势对共振频率、吸收率及品质因子的影响Fig. 5 Effect of Chemical Potential on Resonant Frequency,Absorbance,and Q-Factor
图5(a)展示了不同化学势下吸收器的吸收光谱,其峰值吸收率均超过90%,且随着化学势的增加,吸收峰位发生急剧蓝移.从图5(b)可知:当化学势从0.30 eV增加到0.55 eV时,M0模式的共振频率从5.517 THz增加到7.447 THz,吸收峰的可调范围是1.930 THz;M1模式的共振频率从7.786 THz增加到10.528 THz,吸收峰的可调范围较宽,为2.742 THz.这说明双频窄带吸收器具有较好的频率调谐性能,能够在较宽的频率范围内工作.从图5(c)可知,当化学势从0.30 eV增加到0.55 eV时,吸收器的2个共振频率均先升高后降低,在μc=0.40 eV附近时,到达最高点.从图5(d)可知,当化学势从0.30 eV增加到0.55 eV时,M0模式品质因子变化较小,而M1模式的品质因子急剧减小,当μc=0.30 eV时,M1模式的品质因子高达282.00,而当μc=0.55 eV时,品质因子减小到151.86.
吸收器几何尺寸对吸收特性的影响如图6所示.

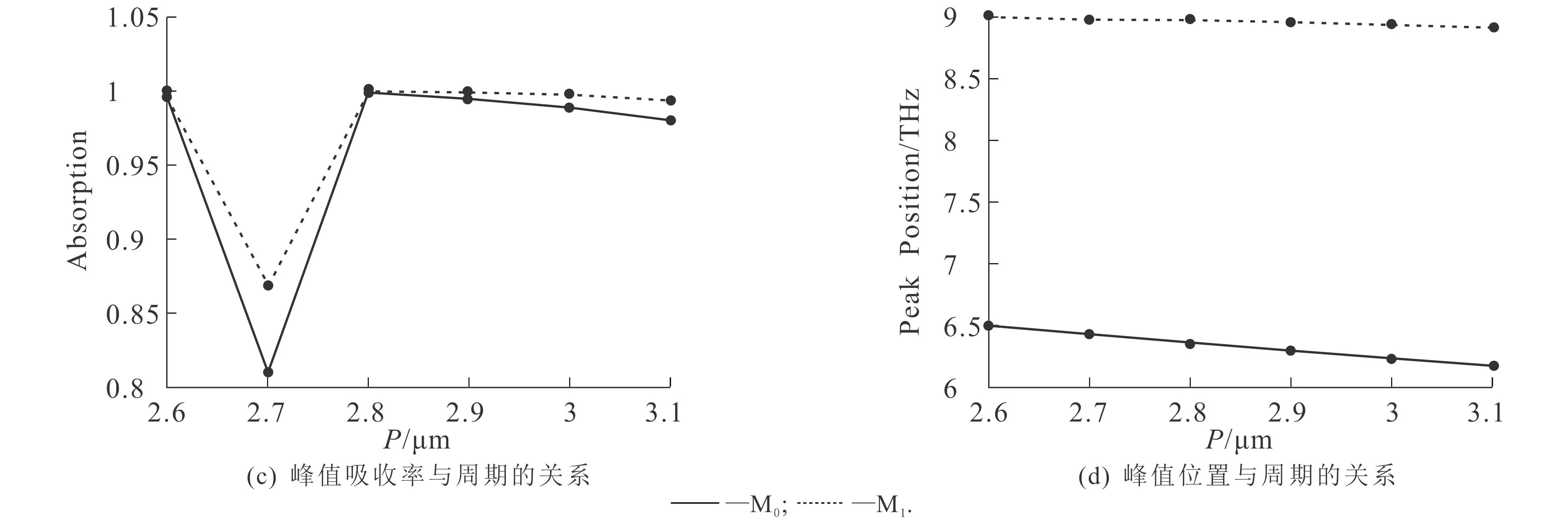
图6 吸收器几何尺寸对吸收率和共振频率的影响Fig. 6 Effect of Geometric Dimensions on Absorbance and Resonant Frequency
图6(a)和图6(b)分别展示了SiO2介质层厚度(td)对吸收率和峰值位置的影响.当td从1.6 μm增加到5.1 μm时,M0模式和M1模式的吸收率均呈现出先升高后降低的趋势,当td在3.1 μm附近时,2个模式的吸收率均接近100%(图6(a));而吸收峰位几乎与td无关(图6(b)).图6(c)展示了周期对吸收率的影响.从图6(c)可知:当P从2.6 μm增加到3.1 μm时,M0模式和M1模式吸收率均先急剧降低,然后急剧升高,最后缓慢降低;当P在2.7 μm附近时,2个共振模式的吸收率都较低,均低于90%;当P在2.8 μm附近时,2个共振模式都能实现完美吸收;而当P进一步增加到3.1 μm时,2个共振模式的吸收率分别缓慢降低至98.0%和99.4%.图6(d)展示了周期对峰值位置的影响,随着P的增加,M0模式和M1模式的共振峰频率都出现了红移,且M0模式的共振峰频率红移较为明显.这是因为表面等离子体激元的共振频率可描述为[16]
(4)
其中:εgra代表石墨烯的介电常数;εd代表SiO2的介电系数;m代表衍射阶数.由(4)式可知,P增加会导致共振频率降低,因而双频超材料太赫兹吸收器吸收共振频率会发生红移.

图7 电场z分量分布的x-y截面Fig. 7 x-y Cross-Sectional Plots of the z-Component Distribution of the Electric Field
为了进一步解释石墨烯可调谐双频完美吸收器的吸收机制,笔者绘制了垂直入射且偏振角为0°时石墨烯表面的Ez电场(沿z方向的电场)分布(图7).
从图7(a)可知,当入射频率为6.363 THz(M0模式)时,左右两边电场符号相反,电荷在左右两边来回振荡,呈现出明显的偶极共振模式.从图7(b)可知,当入射频率为8.987 THz(M1模式)时,电场呈现出高阶共振模式.因此,当吸收器与外部电磁波相互作用时,会发生强烈的电磁共振[23],进而形成2个接近100%的完美吸收峰.
3 结论
笔者设计了一种结构简单的石墨烯可调谐双频完美吸收器,该吸收器在6.363 THz和8.987 THz处的吸收率分别为99.98%和99.99%,与耦合模理论给出的结果基本一致,证实了吸收器的完美吸收主要来源于临界耦合.此外,该吸收器具有优异的偏振不敏感特征,对0°~80°范围内的任意偏振角,其峰值吸收率均超过90%.本研究发现,通过控制石墨烯化学势,可大范围动态调节吸收器的共振频率和品质因子.当化学势从0.30 eV增加至0.55 eV时,吸收峰位发生急剧蓝移,M0模式的共振频率蓝移1.930 THz,M1模式的共振频率蓝移2.742 THz.对于品质因子,M0模式的品质因子变化较小,位于180附近,M1模式的品质因子急剧减小,从282.00减小至151.86.本研究还发现,SiO2介质层厚度对共振峰位几乎没有影响,但对峰值吸收率有一定影响,随着td的增加,吸收率呈现先升高后降低的趋势,在td=3.1 μm附近达到完美吸收.吸收峰位随着周期的增加缓慢红移,峰值吸收率在P=2.8 μm时实现完美吸收,且随着P的增加几乎不变.通过对共振频率处的电场模式进行分析,笔者发现该吸收器的高吸收率主要源于电磁共振作用.
