透射型声超表面斗篷的设计*

隋玉梅,孔 鹏,邓 科,赵鹤平,2

(1.吉首大学物理与机电工程学院,湖南 吉首 416000; 2.湖南财政经济学院,湖南 长沙 410000)

声学人工结构声隐身是一种声波调控的特殊应用,在军事领域具有巨大的应用前景.当声波遇到障碍物时会发生散射,对散射场进行分析就可以得到有关障碍物的信息.声隐身是通过设计声斗篷来对由障碍物引起的散射场进行调控,抑制散射声波,从而隐藏障碍物的特征使它无法被探测到.声斗篷大致包括反射型斗篷[1-4]和透射型斗篷[5],2种斗篷分别主要基于广义Snell定律[6]和变换声学理论来实现[7].近年来,学界涌现出许多利用零折射率声子晶体及五模材料[8-9]制作的声学器件,为后续研究提供了新的思路.大多数基于变换声学——坐标变换理论构建的非均匀各向异性材料的隐身壳[10-11]及利用狄拉克锥的声子晶体等实现的斗篷,其本身厚度大多远大于入射波的波长,尤其当障碍物形状不规则时,对应的斗篷厚度会更厚,这在一定程度上限制了该类斗篷在实际生活中的应用.超表面的出现,对声学斗篷的适用性起到了巨大的推动作用.超表面通可认为是超材料[12]的二维版本,可用于亚波长尺寸的波前处理,即在界面处通过引入亚波长结构来引起突变相位,进而实现对声波的操控[13].根据广义Snell定律[6],在超表面上引入梯度相位,可以控制声波传播.该方法为设计亚波长厚度和简单材料参数的声学斗篷提供了思路[14].基于此,笔者拟以2种超表面(相位调控超表面和近零折射率超表面)结合的隐身机制[5]进行声斗篷设计.相位调控超表面围绕在近零折射率超表面外侧,可以操纵入射波或出射波的波前[15],而近零折射率超表面可以引导垂直入射的声波绕过障碍物,并使入射波垂直于超表面出射[5].将2种超表面进行结合可以控制透射波沿原始入射方向传播,同时抑制散射波,使障碍物无法被探测到.

1 超表面单元的构建

1.1 透射型声斗篷的设计原理

超薄透射型声学斗篷理论模型由2层相应的超表面单元离散而成(图1).外层起相位调控作用,在保证高透射率的基础上进一步调节参数可得相应的相位;内层为近零折射率超表面,作用是引导从外层射入的声波绕过障碍物,让声波沿着原路顺利出射,以达到隐身的效果.

图1 相关原理示意Fig. 1 Related Schematic Diagram

1.2 内层近零折射率超表面

当声波穿过外层相位调控超表面到内层时,内层超表面单元的性质决定了外层需要提供的相位延迟.接下来,首先研究具有迷宫结构的近零折射率超表面的特性.因为方形迷宫单元在实现声波调控时是周期排列的,所以可类比于声子晶体,通过探究其能带结构进一步研究其声学特性.于是,利用COMSOL Multiphysics软件绘制相应的能带结构图(图2(a)),图中波矢沿路径M—Γ—X—M扫描.从图2(a)可知,频率为4 960 Hz时,布里渊区中心Γ点处的能带结构类似一个狄拉克锥,能带结构中存在1条平带,这条平带的存在说明超表面可能是近零折射率材料.因此,在4 960 Hz处有可能实现近零折射率超表面层.

然后,通过等效参数计算法验证超表面近零折射率特性.从图1(b)可知,声波进入超表面空间后,部分反射,部分透射.空气的密度ρ1=1.21 kg/m2,声速c1=343 m/s.将超表面的密度和声速分别设定为ρ2,c2,则空气部分和均匀介质部分的声阻抗可分别表示为Z1=ρ1c1,Z2=ρ2c2,超表面的反射系数、透射系数可分别表示为

(1)

(2)

其中:ω=2πf,f为入射平面波频率;L为超表面宽度.联立(1)式和(2)式可得超表面的密度、声速:

(3)

(4)

(5)

将(4),(5)式代入(3)式,即可得到有效密度.单元结构在4 500～5 500 Hz范围内的有效密度实部和透射率分别如图2(b),(c)所示.由图2(b),(c)可知,4 960 Hz时,单元结构的等效密度实部接近于0,透射率接近于1.这些结果说明在4 960 Hz频率下,单元具有零折射率材料的相关性质,也与能带数据相对应.

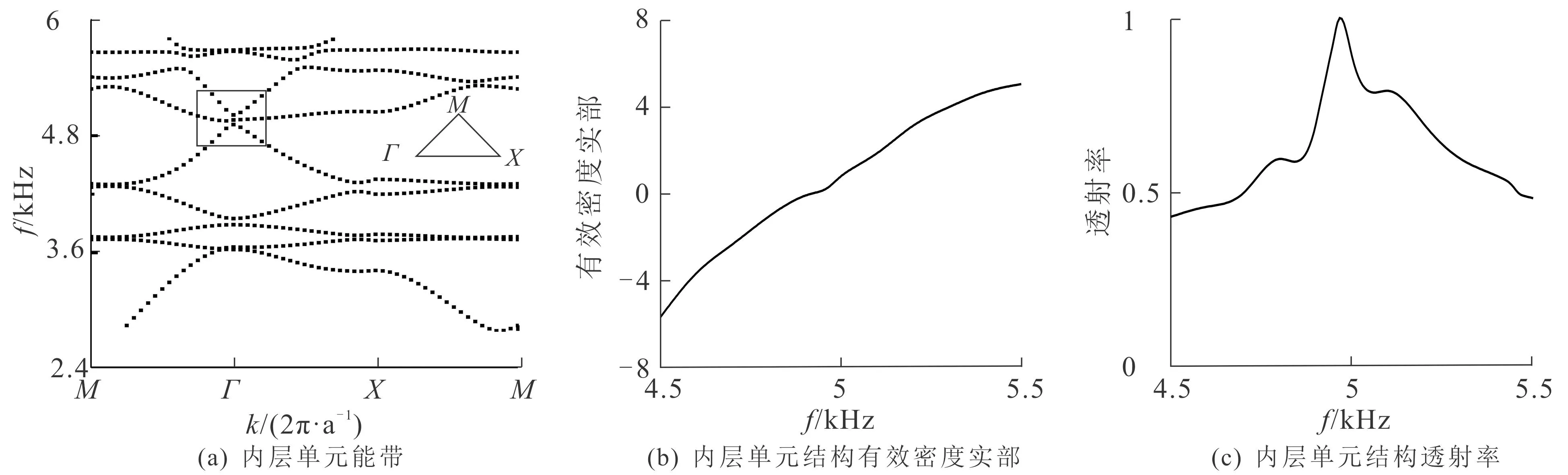
图2 能带及等效参数Fig. 2 Schematic Diagram of Energy Band and Equivalent Parameters

1.3 外层相位调控超表面

外层的相位调控超表面是声阻抗与空气匹配的等效各向异性材料,主要通过广义Snell定律来计算相应的相位[5].所谓广义Snell定律,即在2种介质界面处引入突变相位(界面处声波的振幅、相位等信息会被改变)时,声波从一种介质传播至另一种介质便不再遵循传统的Snell定律(反射角与折射角仅取决于介质的折射率),反射角和折射角不仅与介质的折射率有关,还与所引入的突变相位有关[16].因此,通过对相应突变相位进行设计,即可实现声波调控.广义Snell透射定律原理如图3(a)所示.从图3(a)可知,A点出射的声波经过界面处折射后到达B点.图3(a)中,nt为该超表面的折射率,φ和φ+dφ分别为超表面在C点和O点引入的相位突变,dx为C点到O点的距离.路径A—C—B和A—O—B是相邻声波的传播路径,2条路径无限接近,相位差和声程差均为0.于是

φ+k0ntdxsinθt=φ+dφ-konidxsinθt,

化简可得广义折射定律[7,17],即

在考虑相位调控层时,采用图1(a)中的亥姆霍兹共振结构,以满足结构达到亚波长厚度且具有调制波前的能力.相对于传统意义上的迷宫类结构使声波沿弯曲的路径传播,通过增加传播路径来调控声波的共振结构会更加简单便捷.但声波在亥姆霍兹共振结构中的传播声能会有一定损耗,声波不能完全透射出去.因此,为了实现超常的物理特性,应尽量保持超表面的阻抗与背景介质相匹配,进而实现高透射率.本研究通过合理规划内部管道的个数与尺寸,使超表面能满足[-π,π]范围内的相位变化,并且为了提高声波透射率,还在该共振结构通道的侧边增添直通道.图2显示,超表面在4 960 Hz时具有近零折射率特性.因此,将工作频率设定为4 960 Hz,并把超表面置于波导中,利用COMSOL Multiphysics软件计算4 960 Hz频率下的透射率及更改空腔深度l时的相位,结果如图3(b)所示.由图3(b)可知,在4 960 Hz频率下,更改l能很好地满足[-π,π]范围内的连续相位分布,且透射率均在0.6以上.因此,根据所需的相位延迟就可选择出具有不同l的单元结构进行结构构建.

2 仿真分析

因为正方形障碍物具有对称性,所以进行简化仿真计算,只研究1/4个声斗篷即可(根据声波的互易性,在隐身中设计的相应结构只需分别沿x,y轴做镜面对称).将正方形障碍物及斗篷旋转45°,即声波以45°入射至相位调控层,经过调控,又垂直于相位调控层出射.对相位调控层进行仿真计算,发现声波能达到45°异常折射,声波异常折射结果如图4(a)所示.由图4(a)可知,当声波垂直入射至外层超表面时,经过调控,声波偏转45°出射,满足预期目标的第1步.随后将2层超表面进行组合,设置背景介质ρ0=1.2 kg/m2,c0=343 m/s,通过仿真获得声压场分布,分布结果如图4(b)所示.由图4(b)可知,在4 960 Hz背景压力场激励下,由于声斗篷的存在,因正方形障碍物而变得紊乱的声场得到有效恢复,声波经过超表面时被妥善引导,成功地绕过了障碍物,而后声波沿原始入射方向继续传播,其他方向的散射被有效抑制.由此可知,透射型声超表面斗篷展现出良好的隐身性能.

图4 声场分析Fig. 4 Sound Field Analysis

3 结论

笔者设计了一种混合型的超薄声学隐形斗篷,斗篷由2层超表面组成,可以实现方形障碍物的声隐身.斗篷的2层超表面紧密围绕在障碍物周围,内层是近零折射率层,外层是相位调控层.内层近零折射率超表面实际上等同于一个等相位区域,可以引导入射波绕过障碍物;外层相位调控超表面的主要作用是将入射波垂直传播到内层上,并调控内层垂直出射的声波沿原入射方向传播,进而实现声隐身.这种声斗篷非常薄,厚度仅为工作波长的0.67倍,能紧贴物体表面.仿真结果显示,斗篷在4 960 Hz频率下能有效隐藏方形物体.