基于Python语言的超薄金刚石切割片建模与SiC晶片切割仿真＊

何 艳，李 翔，高兴军，凡 林，刘 铭，徐子成

（辽宁石油化工大学 机械工程学院,辽宁 抚顺 113001）

作为各种电子电力器件中的关键部件，半导体器件受到了越来越多的关注。而单晶SiC凭借着其优异的物理和电子性能从众多半导体材料中脱颖而出，广泛应用于各类半导体器件中[1-4]。SiC是典型的硬脆材料，不仅具有杰出的机械性能，而且具有耐高温、耐高压等优良的电热学性能。SiC切割过程中产生的亚表面损伤、边缘裂纹和残余应力等，不仅影响其优异性能，更降低了半导体器件的可靠性和使用寿命。因此，如何实现SiC的高效率、高质量切割，是SiC切割加工中面临的主要难题。

目前，很多学者对SiC的切割加工方法进行了深入的研究。LEWKE等[5]采用热激光分离方法切割4HSiC，实现了无接触切割且材料无损伤，同时工件表面无裂纹产生，但切割只能沿直线路径进行。激光隐形切割技术是近几年新提出的切割方法，加工原理是将脉冲激光通过光学透镜汇聚，聚焦在内部材料上，仅对材料内部造成损伤。相较于普通激光切割，激光隐形切割技术具有无切口、速度快、可靠性高等优点[6]，然而用其切割硬脆性材料SiC工件时，会导致工件产生崩边和裂纹扩展[7]。ZHANG等[8]在激光隐形切割技术的基础上提出双激光束异步切割法切割SiC，解决了其崩边和裂纹扩展的问题，但这种方法限定工件厚度为200 μm。GE等[9]使用固定磨料线切割单晶SiC，结果表明可以通过控制线切割的张力和弓角实现SiC的无裂纹加工。FUJITA等[10]通过多晶金刚石切割片切割带有金属薄膜的SiC衬底，当切割片转速为30 000 r/min时，SiC和金属薄膜之间没有出现裂纹。CVETKOVIĆ等[11]对比了线切割和切割片切割单晶SiC的壁面粗糙度，线切割时的侧壁粗糙度Ra为2.4 μm，切割片切割时的Ra最小为1.6 μm。因此，切割片切割SiC晶片具有切割质量好，磨粒不易脱落等优点，是学者关注的焦点。

关于切割片切割SiC仿真的研究，大多数文献仍采用单颗金刚石磨粒划擦SiC表征材料去除的过程[12-16]。由于切割片表面的磨粒并不规则，单磨粒划擦的局限性非常明显，建立准确的多磨粒切割片模型显得尤为重要。目前，已有学者建立多种多磨粒模型模拟砂轮或线切割去除SiC等硬脆性材料的过程。TANG等[17-18]建立了磨粒随机分布的金刚石线切割模型，主要研究了切割速度和深度对脆性材料切割效果的影响。YANG等[19-21]对比了砂轮有序磨粒和随机分布磨粒在相同磨削参数下的磨削力，研究表明有序磨粒的磨削力要低于随机分布磨粒的磨削力。此后，LI等[22-23]采用离散元的方法对砂轮进行数学建模。CHEN等[24]在此基础上通过蒙特卡罗方法随机切割球体建立了单磨粒模型，且基于虚拟网格建立了砂轮模型，并通过切削力验证了仿真模型的可靠性。CHEN等[25]仅对砂轮的切割刃部分的切割效果进行了仿真研究，极大地提高了计算速度。ZHANG等[26]构建了一种磨粒出刃高度随机的砂轮模型，可通过控制砂轮表面磨粒的出刃高度调控工件表面粗糙度。WANG等[27]使用Solidworks三维建模软件建立了砂轮模型，并对砂轮磨削SiC复合材料的磨削过程进行仿真，最终仿真与实验的误差在15%以内。

金刚石线切割能够批量切割SiC晶片，但其上的磨粒易脱落，脱落的磨粒会对晶体表面造成损伤。虽然磨粒有序排布的砂轮性能高于磨粒随机分布砂轮的，但在砂轮实际生产中难以控制每个磨粒的准确位置，并且砂轮表面的磨粒分布具有不确定性和随机性，每个磨粒形状无法准确确定。针对上述问题，采用超薄金刚石切割片切割单晶SiC，提出Python语言与Abaqus有限元分析软件相结合的建模方式，建立磨粒随机分布的切割片模型，研究超薄金刚石切割片切割参数对SiC晶片切割边缘完整性、切割力、切割温度及亚表面损伤的影响。

1 模型的建立

1.1 磨粒模型建立

金刚石磨粒形状各不相同，但都趋向于随机多面体，因此以立方六面体为基体对其进行多次切割建立单个磨粒模型，并采用Python语言与Abaqus有限元分析软件相结合的方式建立磨粒和切割片模型。构建单个磨粒所需的随机四边形切割工具如图1所示，其构建过程如下：首先以O为圆心R为半径，在正方形内确定1个圆；然后在第一象限内随机选取角度θ，角度θ的尺寸界线与圆的交点为p，过交点p做圆的切线，因而通过圆切线方程确立了第1条切割线。同理，确定其余3条切割线。4条切割线分别相交于A、B、C、D4点，四边形ABCD即为所构建的切割工具。

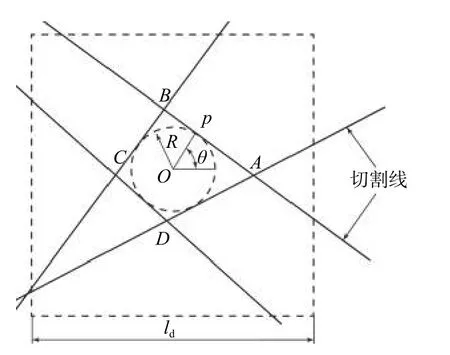
图1 随机四边形切割工具Fig.1 Random quadrilateral cutting tool

四边形切割工具切割立方六面体的流程如图2所示，第1次切割完成后，将磨粒旋转任意角度，再对其进行第2次切割，以确保磨粒形状结构的随机性。由图2可知：随着切割次数的增加，获得了不同形状的表面，其三维结构更趋向于金刚石磨粒结构。由于过多的切割会导致磨粒趋向于球体，因此将切割次数设定在6～9次。

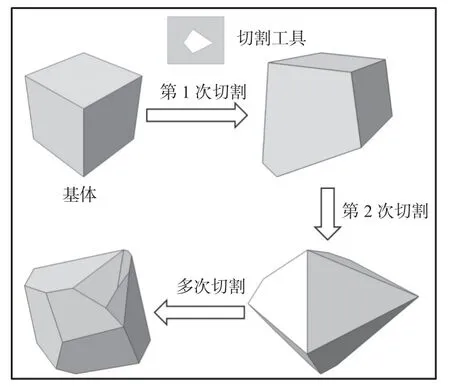
图2 磨粒切割流程图Fig.2 Flow chart of abrasive cutting

切割片磨粒粒度、磨粒粒径和磨粒浓度之间的关系式为[28]：

式中：dgavg为磨粒的平均粒径，M为金刚石磨粒粒度号（用目数表示），Vs为磨粒的浓度，S为切割片组织号。

以直径为58 mm，厚度为0.2 mm，磨粒粒度号为400，磨粒浓度为25%的金刚石切割片为例，根据式（1）计算出金刚石切割片磨粒的平均粒径为38 μm。

由于金刚石磨粒的粒径分布规律符合正态分布函数[29]，磨粒粒径分布概率为：

式中：x为磨粒粒径，σ1为正态分布标准差，μ1为正态分布均值，xmax和xmin分别为磨粒的最大粒径和最小粒径。

筛选粒径范围在xmax和xmin之间的磨粒，构建的磨粒形状模型库如图3所示。

图3 磨粒模型库Fig.3 Abrasives model library

1.2 超薄切割片模型建立

（1）采用Python语言中的Random函数随机排布切割片表面的磨粒，根据磨粒的平均粒径与浓度计算两磨粒之间的距离lg，其式为：

然后，将磨粒整齐排布在切割片表面，对每个磨粒施加随机位移以确保磨粒分布的随机性。由于切割片外轮廓具有一定弧度，因此将极坐标系（r，θ，z）转化为Abaqus可识别的直角坐标系（x，y，z），得到：

采用式（7）对每个磨粒施加xy平面上的位移，则：

式中：xmn，ymn是第m个磨粒在xy平面上的最终坐标，xm0，ym0是第m个磨粒在xy平面上的初始坐标，δx和δy分别是磨粒在x轴和y轴上的随机位移量。

（2）确定磨粒在z方向的位置，即确定磨粒在砂轮表面的出刃高度。磨粒出刃高度符合正态分布函数式（3）及式（4），式中的参数x为磨粒出刃高度，xmax和xmin分别为磨粒出刃高度的最大值和最小值。图4为砂轮表面磨粒出刃高度概率示意图，其上半部分为磨粒出刃高度的正态分布曲线，下半部分为磨粒出刃高度示意图。由图4可知，大多数磨粒出刃高度位于平均出刃高度附近。随着磨粒的出刃高度高于或低于平均出刃高度，其分布概率逐渐降低。

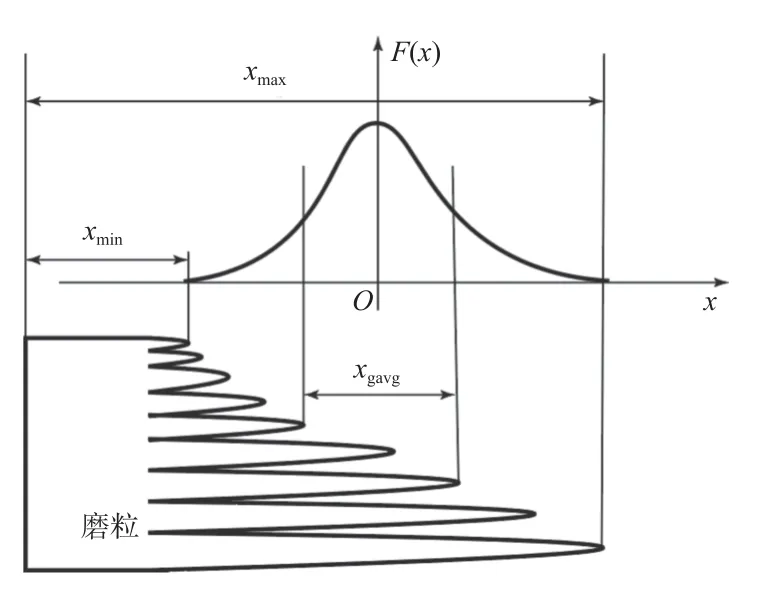
图4 磨粒出刃高度概率示意图Fig.4 Probability diagram of abrasive grain protrusion height

（3）将磨粒与砂轮基体组合，构建的金刚石切割片表面磨粒分布模型如图5所示。截取切割片整圆中的1°作为砂轮基体，基体近似为0.20 mm× 0.50 mm×0.02 mm的六面体。由于模拟切削的时间较短，一般不会产生磨粒脱落的情况，因此可将磨粒与切割片基体合为一体。

图5 切割片表面磨粒分布模型Fig.5 Model of abrasive particle distribution on the surface of cutting slice

1.3 超薄金刚石切割片切割SiC晶片模型建立

超薄金刚石切割片切割SiC晶片模型如图6所示。图6中：切割片沿x方向运动，切割过程中SiC晶片底部设置为完全固定。选择能够准确计算SiC在大应变和高应变率下的力学响应和破坏行为的JH-2本构模型[30]，常温下单晶SiC JH-2本构模型的材料参数如表1所示[31]。DS610精密划片切割机的转速为20 000～40 000 r/min，其金刚石切割片的直径为58 mm，以此为参考，计算出砂轮的线速度为60～121 m/s。分析步类型为温度位移耦合，初始温度设定为20 ℃。网格单元类型设置为C3D8RT六面体网格，对切割区域网格进行局部细化处理。切割过程中的参数设置如表2所示。

表1 常温下SiC的物理性能参数Tab.1 Physical property parameters of SiC at room temperature

表2 切割过程的参数设定Tab.2 Parameter setting of cutting process

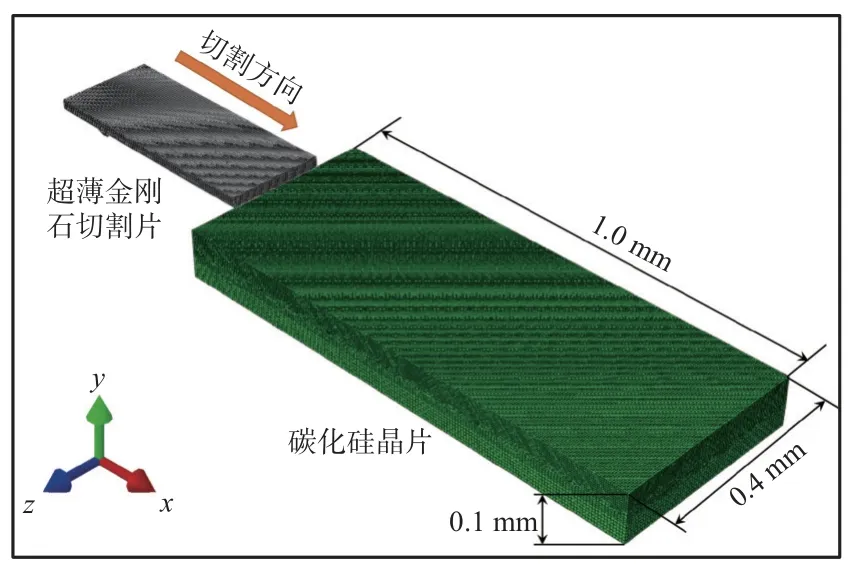
图6 超薄金刚石切割片切割SiC晶片模型Fig.6 Model of cutting SiC wafer with ultra-thin diamond slice

2 结果与讨论

2.1 超薄金刚石切割参数对切割力的影响

切割力是切割过程中工件抵抗切割片切割产生的阻力，一些学者[12,32-33]已经对SiC加工过程中刀具所受阻力进行了研究。正确分析切割片在切割过程中切割力的大小及变化规律，是研究切割热与工件切割边缘完整性的重要依据。

当表2中切割速度为76 m/s，其他条件不变时，超薄金刚石切割片的切割深度对切割力的影响如图7所示。由图7a可知：主切割力Fx、法向切割力Fz和轴向切割力Fy均随切割深度的增加而增大，整体上呈线性上升趋势。主切割力Fx的方向与切割片运动的x方向相同，Fx值最大；法向切割力Fz沿z方向，Fz值次之；轴向切割力Fy为切割片所受y方向的挤压力，Fy值最小。当切割深度在6～9 μm时，3个切割分力急剧增长。其可能的原因为切割片表面磨粒出刃高度为正态分布，当切割深度为6～9 μm时与正态分布函数的中间段对应，此时大量磨粒参与SiC晶片的材料去除，磨粒对晶片的有效去除面积较大，因此切割分力增长更快。当切割深度＞9 μm时，切割片表面磨粒均参与材料的去除，增大切割深度，其有效去除面积增长较缓慢，因此切割分力的增长趋势减缓。

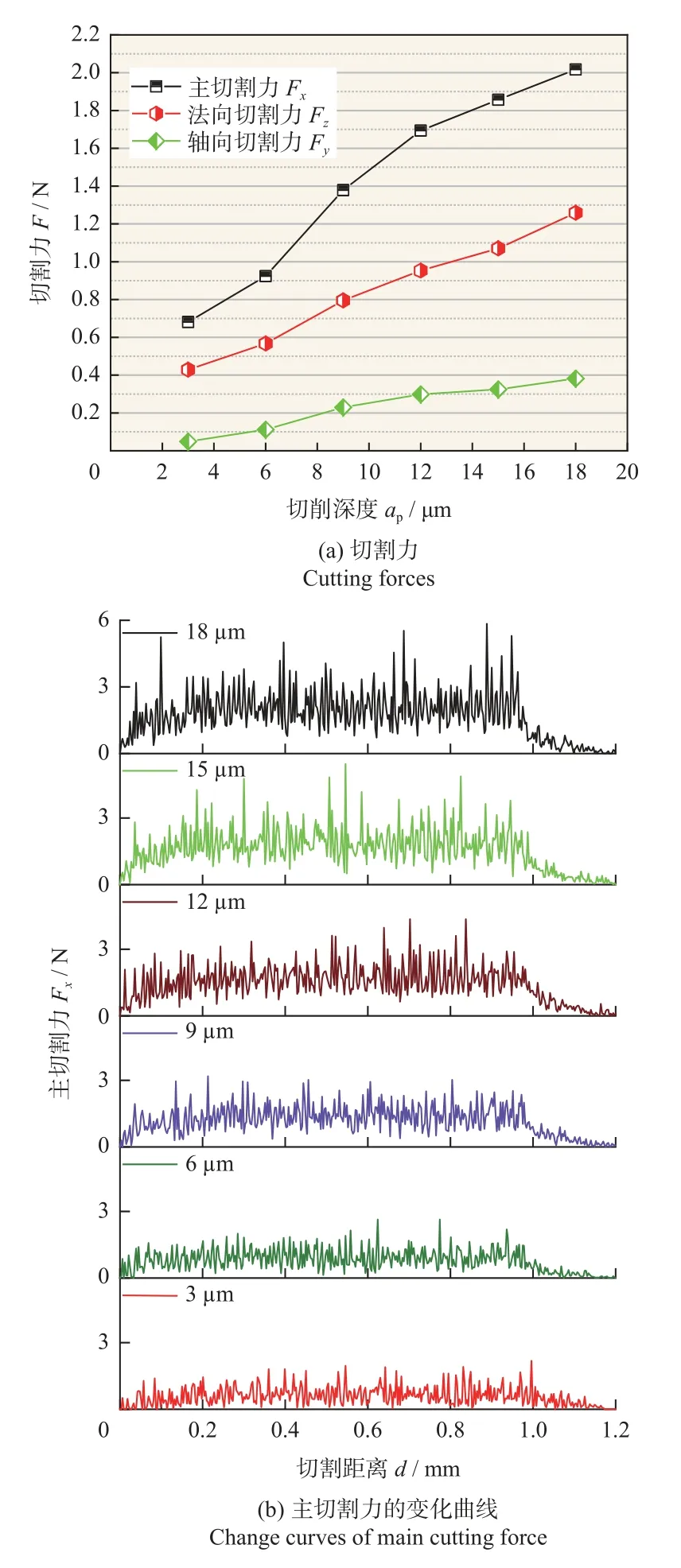
图7 切割深度对切割力的影响Fig.7 Effect of cutting depths on cutting forces

由图7b可知：切割深度越大，主切割力Fx的波动值越大。且切割过程中的力波动幅度都呈现逐渐增大、稳定波动和逐渐减小3个阶段，分别对应切割过程中的切入阶段、稳定切割阶段和切出阶段。

当切割深度为9 μm，其他条件不变时，超薄金刚石切割片的切割速度对切割力的影响如图8所示。由图8a可知：当切割速度在60～121 m/s时，主切割力Fx、法向切割力Fz和轴向切割力Fy变化极小。由图8b可知：不同切割速度下主切割力的波动幅值无明显差异，且切割过程中主切割力的变化趋势相同。因此，切割速度对切割力的影响较小，切割速度是非显著因素。

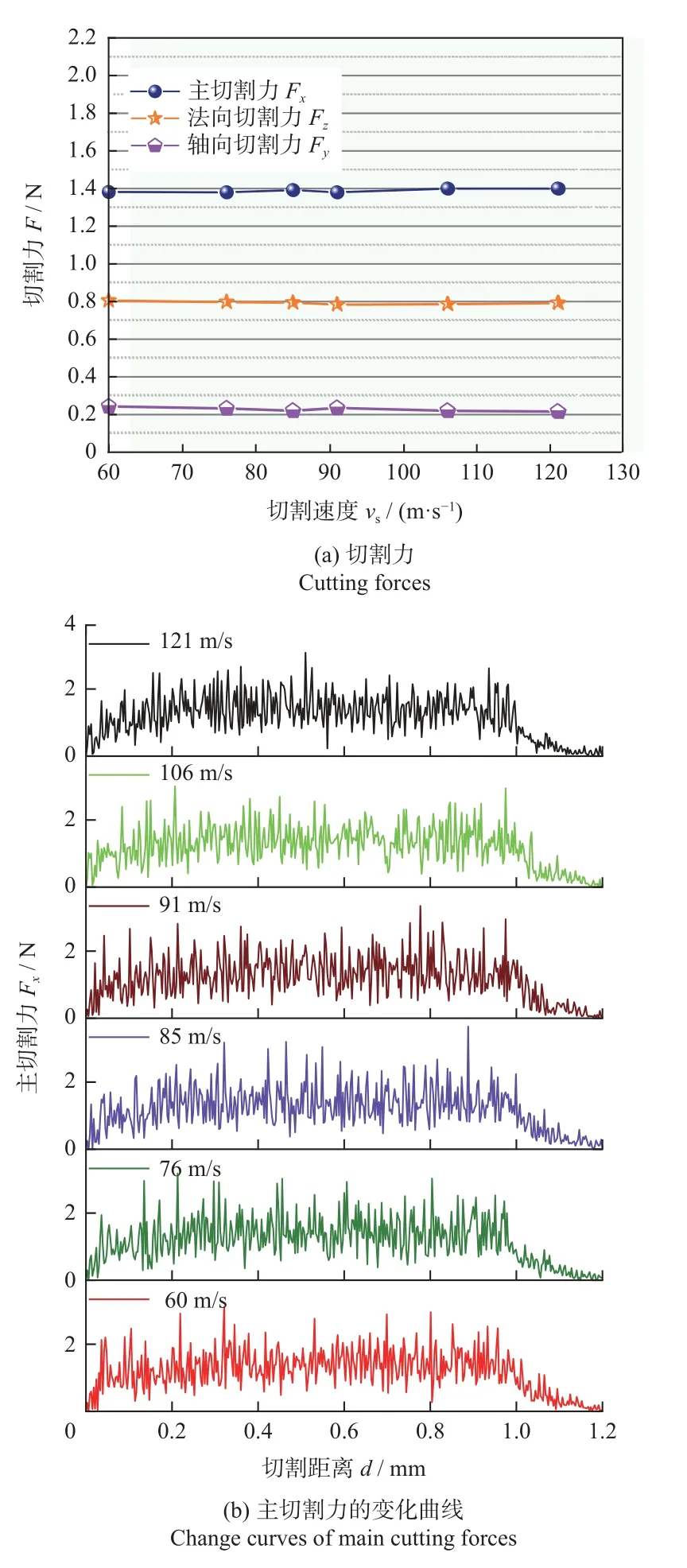
图8 切割速度对切割力的影响Fig.8 Effect of cutting speeds on cutting forces

2.2 超薄金刚石切割参数对温度的影响

材料加工过程中产生的热量对工件应力应变有非常重要的影响，一些学者[34-36]采用不同的仿真方法分析了硅等脆性材料磨削过程中砂轮和磨粒产生的磨削热。切割片的切割过程与砂轮磨削过程极为相似，因此研究切割过程中产生的热量及其变化规律对切割质量及其热应力分析有十分重要的意义。

通过将磨粒与磨粒上的一点进行耦合处理，提取磨粒表面温度与切割距离之间的关系；再通过Python编程语言提取切割过程中晶片的最高温度与切割完成后晶片整体的平均温度，温度的提取精度为0.001 ℃。

在SiC晶片材料去除的过程中，与晶片接触的砂轮前端的数个磨粒起主要切割作用。因此，可通过提取有效切割磨粒的温度，分析切割片的温度变化趋势。当切割速度为76 m/s时，切割片的磨粒表面温度随切割深度的变化如图9a所示。由图9a可知：在不同切割深度下，磨粒与SiC晶片不断的挤压、摩擦，因此随着切割距离的增加，磨粒表面温度呈现波动上升趋势。当切割距离超过1.0 mm时，切割片处于切出工件阶段，此时磨粒与SiC晶片不再接触，磨粒表面温度经过小幅下降后保持稳定。当切割深度较小为3 μm时，仅有磨粒的某一尖角起主要切割作用，因此磨粒表面温度波动幅值较大；随着切割深度的增加，磨粒表面温度的上升趋势更急剧，总体上磨粒表面温度与切割深度的变化趋势呈正相关，可通过控制切割片的切割深度调控切割片表面的磨粒温度。

图9 切割片的磨粒表面温度Fig.9 Abrasive surface temperatures of cutting slices

当切割深度为9 μm时，切割速度对磨粒表面温度的影响如图9b所示。从图9b的最高温度处的局部放大图中可以看出：磨粒表面的最高温度随切割速度增大略有上升，但观察整体图可以发现切割速度对磨粒表面最高温度的影响较小。因此，从磨粒最高温度的角度进一步验证了切割速度对热应力的影响较小。

超薄金刚石切割片的切割参数对SiC晶片平均温度与最高温度的影响如图10所示。图10a为切割速度为76 m/s时晶片平均温度与最高温度随切割深度的变化。从图10a中可以看出，最高温度远大于平均温度。这是因为最高温度从切割过程中产生的碎屑温度中提取，当碎屑与晶片分离的瞬间存在巨大的能量，碎屑温度主要由内能（磨粒与晶片相互作用产生）转化而成，因此最高温度极高；而平均温度是切割完成后晶片整体的平均温度，切割过程中仅在晶片切割区域具有较高的温度，而切割区域占比较小（＜15%），因此晶片整体的平均温度较低。图10a中：随着切割深度增加，晶片平均温度与最高温度均呈上升趋势，与磨粒表面温度变化趋势一致（图9a）。同时，与最高温度比，晶片平均温度的上升趋势更加平稳。因此，由于SiC为典型的脆性材料，其切割过程中会产生大量的细小碎屑，碎屑的温度随切割深度的增加而呈不断上升的趋势。

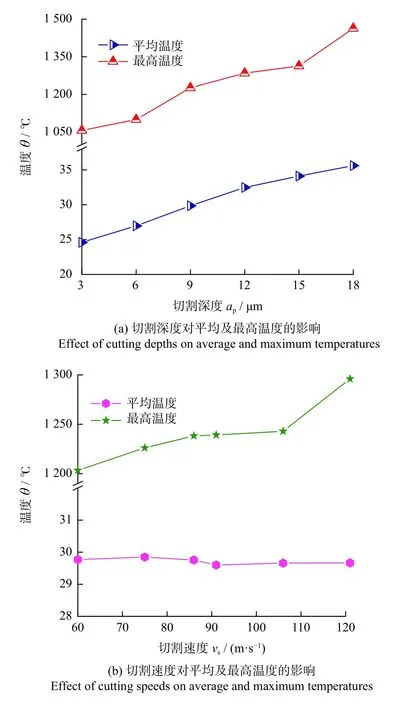
图10 SiC晶片的平均温度与最高温度Fig.10 Average and maximum temperature of SiC wafer

图10b为切割深度为9 μm时晶片的平均温度与最高温度随切割速度的变化。从图10b中可以看出：切割速度的增大对SiC晶片平均温度影响较小，而随切割速度的增大其最高温度展现出逐渐增大的趋势，但增大幅度小于切割深度时的。

2.3 SiC晶片切割边缘形貌分析

SiC晶片切割过程中的切割边缘会出现不同程度的崩碎和裂纹[37-39]。为了研究切割参数对晶片切割边缘形貌的影响，对切割边缘进行切片处理，由于切割片在走刀阶段会带走大量材料而影响晶片边缘形貌的观测结果，因此选取晶片切削距离为0～0.8 mm时的位置进行研究。图11为切割速度为76 m/s时不同切割深度下SiC晶片切割边缘形貌图。由图11可知：当切割深度为3 μm时，仅有不规则的磨粒尖端部分对晶片材料起去除作用，切割区域承受的单位压力大。此外，切割片表面磨粒的出刃高度各不相同，切割片切割深度较浅时，磨粒的出刃高度差也将增大晶片表面的损伤，从而导致晶片切割边缘崩边严重，切割质量较差。当切割深度为6～9 μm时，磨粒的切入深度处于正态分布的中间段，大量磨粒参与晶片材料的去除，材料呈现稳定去除状态，晶片边缘崩碎较轻，质量较好；随着切割深度的进一步增大，晶片切割边缘损伤宽度增大，较大的切割深度降低了晶片切割边缘的质量。

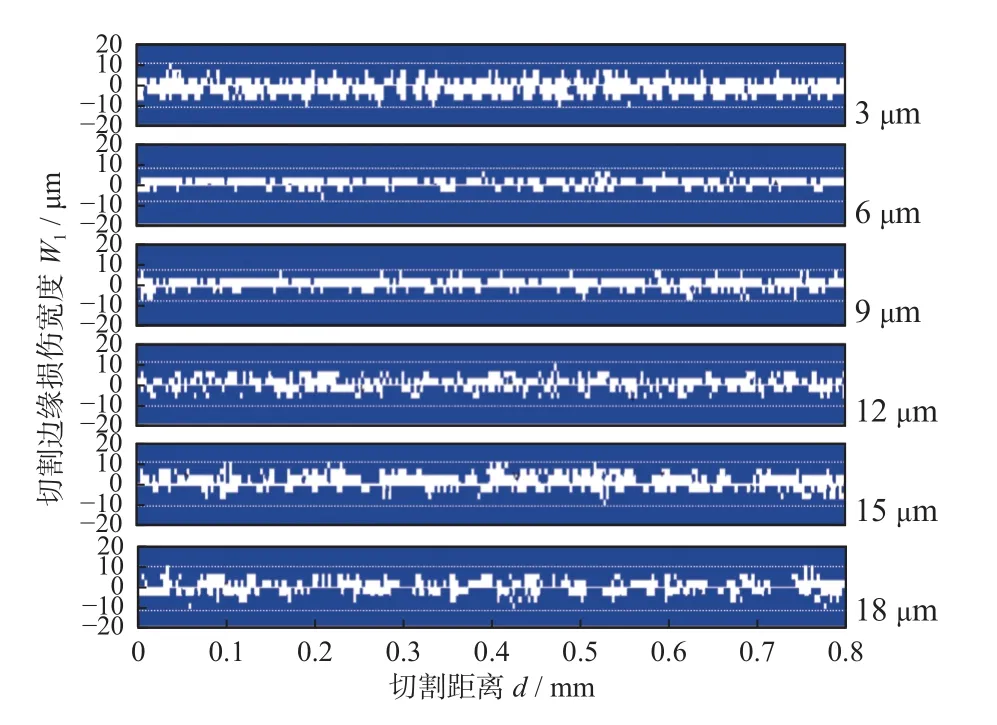
图11 切割深度对SiC晶片切割边缘形貌的影响Fig.11 Effect of cutting depths on cutting edge morphology of SiC wafer

图12所示为切割深度对SiC晶片切割边缘损伤宽度和损伤面积的影响，此时切割速度为76 m/s。由图12可知：随切割深度的增大，晶片切割边缘损伤宽度与边缘损伤面积都呈先减小后增大的趋势。当切割深度为6 μm和9 μm时，切割边缘损伤宽度最小值为8 μm；当切割深度为6 μm时，最小损伤面积为4 905.56 μm2；且切割深度＞6 μm时，边缘损伤面积值随着切割深度的增大而增大。合理的切割深度，不仅可获得较好的切割边缘，还有助于抑制晶片切割边缘碎裂的形成；切割深度过大，将会破坏切割边缘完整性，并增大晶片的损伤宽度值。

图12 切割深度对SiC晶片切割边缘损伤宽度和损伤面积的影响Fig.12 Effect of cutting depths on damage widths and damage area of cutting edge of SiC wafer

图13为切割深度为9 μm时不同切割速度下SiC晶片切割边缘形貌图。由图13可知：当砂轮切割速度为60～121 m/s，切割片处于高速切割阶段，随着切割速度的增加，晶片切割边缘质量逐渐改善。

图13 切割速度对SiC晶片切割边缘形貌的影响Fig.13 Effect of cutting speeds on cutting edge morphology of SiC wafer

图14为切割深度为9 μm时切割速度对晶片切割边缘损伤宽度及损伤面积的影响。由图14可知：当切割速度在60～121 m/s时，晶片切割边缘损伤宽度呈水平稳定状态；而当切割速度为76和121 m/s时，晶片边缘损伤面积较小。因此，切割速度对切割边缘形貌的影响较小，这是因为在高速切割阶段，SiC切割过程中的表面损伤主要以微裂纹损伤为主。从材料去除层面分析，微裂纹是由晶体的位错和层错产生的[40]；位错密度主要受切割速度的影响，当切割速度较高时位错密度也会增大[31]，进而导致大量微裂纹的萌生；但微裂纹损伤深度小于一个晶粒尺寸的大小，未穿越晶界，因此高速切割下切割速度对切割损伤层的影响较小。从力学层面分析，当切割速度较低时（≤15 m/s），切割速度对SiC损伤层深度影响较大，因为低速切割会产生较大的应力集中，导致产生较大的裂纹（＞50 μm）[41]；而高速切割所产生的微裂纹比较密集，在其萌生扩展过程中相互交汇，消耗了大量的能量，解决了低切割速度下的应力集中问题，无法形成较大的裂纹，因此高速切割下切割速度对切割边缘形貌影响较小。

图14 切割速度对SiC晶片边缘损伤宽度和损伤面积的影响Fig.14 Effect of cutting speeds on damage widths and damage area of cutting edge of SiC wafer

2.4 SiC晶片亚表面损伤分析

切割深度不仅影响切割边缘的完整性，还对SiC的亚表面损伤有着较大的影响[42-44]。由于切割速度对SiC亚表面损伤的影响较小，在此将不再赘述，只考虑切割深度的影响。图15为切割速度为76 m/s时不同切割深度下SiC晶片亚表面损伤的切片云图。从图15可知：随着切割深度的增大，晶片的亚表面损伤层深度增大，其应力影响区域也在不断扩大。当切割深度最大为18 μm时，晶片的亚表面层不仅在出刀位置存在较大的损伤，在稳定切割阶段也出现了较大的凹坑。

在切割速度为76 m/s时，切割片的切割深度与SiC晶片亚表面损伤深度及切面损伤面积关系如图16所示。由图16可知：随着切割深度的增加，SiC晶片亚表面损伤深度及损伤面积先减小后增大，与SiC晶片边缘形貌的分析结果一致（图12）。与切割深度为6 μm相比，当切割深度较低为3 μm时，SiC晶片的亚表面损伤深度与损伤面积较高，此时晶片承受的单位压力和磨粒的出刃高度是影响其切割损伤的因素。当切割深度为6 μm时，亚表面损伤深度达到最低值10.67 μm，损伤面积达最小值7 022.18 μm2。当切割深度＞6 μm时，SiC晶片亚表面损伤深度与损伤面积随切割深度的增大呈线性上升趋势。所以，切割深度对SiC晶片亚表面损伤深度及损伤面积的影响较大，控制切割片的切割深度能有效提高晶片加工质量。

3 结论

（1）Python语言能够实现磨料形状的随机切割和磨粒的随机正态分布，采用Python语言与Abaqus有限元分析软件相结合的方式建立了磨粒模型库和超薄金刚石片切割SiC晶片的模型。

（2）随着超薄金刚石片切割深度的增大，切割力、金刚石磨粒和晶片的温度增大，SiC晶片切割边缘损伤程度和亚表面损伤深度先减小后增大。当切割深度为6 μm时，晶片切割边缘的损伤宽度和损伤面积分别达到8 μm和4 905.56 μm2的最小值，且晶片的亚表面损伤深度和损伤面积也分别达到10.67 μm和7 022.18 μm2的最小值。

（3）在超薄金刚石切割片高速切割阶段（切割速度为60～121 m/s），切割速度对切割力、温度、晶片切割边缘形貌和亚表面损伤的影响较弱。因此，在不影响切割质量的情况下，提高切割速度将是提高晶片切割效率最有效方法。