钢管混凝土风电塔架球式节点的力学性能分析

2023-12-21李兆建

西南交通大学学报 2023年6期

闻洋，李兆建，于蛟

（内蒙古科技大学土木工程学院，内蒙古包头 014010）

随着“碳达峰、碳中和”目标的提出，风能作为一种清洁、绿色的可再生能源[1]，运用风力发电将迎来大规模的加速发展期.据有关研究表明[2]，高度在100 m 以上时风况更好，所以对风力发电塔架的高度、稳定性等方面提出了更高的要求.格构式风电塔架具有运输便利、安装简便、结构刚度大等特点，且具有良好的受力性能，综合效益更高[3-6].

目前，在钢管混凝土格构式风电塔架中的节点多为焊接节点[7-15]，但其存在高空施焊困难、焊接残余应力等弊端，使其受力更加复杂，进而影响塔架的承载能力.

基于以上问题，本文提出了2 种节点：法兰盘球型分支节点和法兰盘螺栓球节点.前者因其有外螺栓球的存在，连接时的角度比较灵活，腹杆与塔柱间的夹角在设计时可选范围广，几何适应性好，但由于腹杆合力点交于外螺栓球，合力点距球台核心区较远，易发生偏心受力，结构适应性较差；后者因其腹杆合力点直接交于球台内的螺栓球上，内力传递简单，整体设计协调，结构适应性较好，但在设计时由于腹杆与法兰盘距离太近，腹杆与塔柱间的夹角可选范围小，装配时可操作空间小，几何适应性稍差.因此，为了选出综合性能较好的球式节点，对2 个法兰盘球型分支节点和2 个法兰盘螺栓球节点进行了对比试验研究和有限元分析，研究2 种节点在不同球台高度h和厚度b条件下的破坏模式、法兰盘等效应力分布、腹杆轴力-变形曲线等性能，为球式节点的优化设计提供理论指导.

1 试验概况

1.1 试件设计

以内蒙古白云鄂博地区某1.5 MW 的锥型风电塔筒为原型，设计四肢柱钢管混凝土格构式风电塔架.使用SAP2000 分析其内力，并考虑加载设备及试验场地大小有限，按1∶1.6 设计4 个法兰盘球式节点缩尺试件，变化参数为球台的高度h与厚度b.试件塔柱采用无缝圆钢管，内填混凝土，上、下侧2 片包裹体包裹在塔柱上并用M20 的10.9 级高强螺栓连接，球台焊接在包裹体上，螺栓球置于球台内，法兰盘采用同样的高强螺栓与球台板连接以固定内螺栓球，法兰盘球型分支节点采用双螺纹连接杆和外螺栓球形式，把腹杆与球台内螺栓球连接在一起，而法兰盘螺栓球节点直接把腹杆与球台内螺栓球连接在一起.节点材质均为Q235 钢，腹杆采用Q235无缝钢管.试验前进行材性试验，测得C40 混凝土28 d 立方体的抗压强度为43.8 MPa.节点见图1，试件参数见表1，钢材力学性能指标见表2.表2 中：fy为屈服强度；fu为抗拉强度；E为弹性模量

表1 试件参数Tab.1 Specimen parameters

表2 钢材力学性能指标Tab.2 Mechanical property indexes of steels

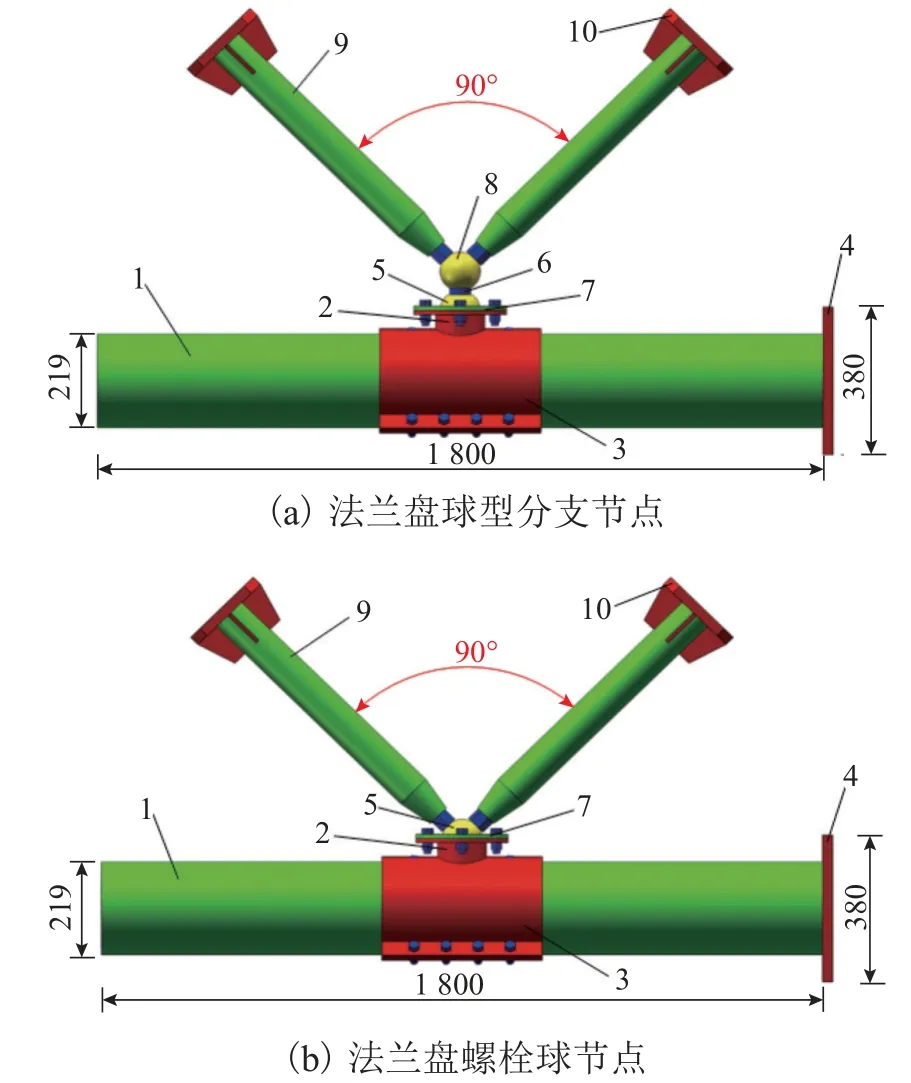
图1 节点示意Fig.1 Schematic of joints

试验使用卧式加载装置.如图2 所示，塔柱一端通过端板与承力支座相连；另一端采用U 型压梁和支撑架固定；拉、压腹杆分别采用加载板与液压伺服器相接.

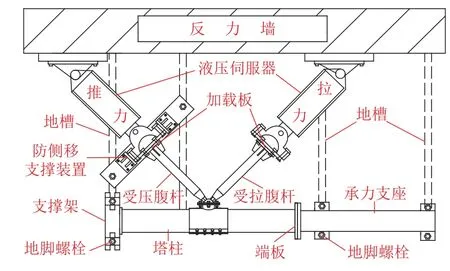
图2 试验加载装置Fig.2 Test loading device

1.2 加载装置和加载制度

试验使用单调静力加载制度，分为预加载、标准加载和破坏加载3 个阶段，由SAP2000 分析，受压与受拉腹杆按照1∶1.09 比例施加荷载.预加载分为3 级，并持荷10 min；标准加载阶段每次取理论极限荷载的10%；进入破坏加载阶段的标志是试件屈服或达到理论极限荷载的85%，为得到试件准确的实际承载力，每级取理论极限荷载的5%，直至试件破坏，停止试验.

2 破坏形态

试件破坏形态如图3 所示.JD-1 发生高强螺栓剪切破坏.当荷载为19 kN 时，连接杆和外螺栓球向拉杆方向开始发生倾斜；当荷载为50 kN 时，连接杆和外螺栓球倾斜明显，并且和法兰盘发生触碰现象；当荷载为78 kN 时，触碰现象明显，其偏心达到最大，导致拉杆方向上套筒与高强螺栓处于受剪状态；最终当荷载为89 kN 时，高强螺栓在剪力持续作用下被剪断，停止试验.JD-2 的破坏形态与JD-1 基本相似，试件均发生高强螺栓剪切破坏.JD-3 发生球台底部焊缝撕裂破坏.当荷载为190 kN 时，在球台底部焊缝处开始出现微小裂缝；当荷载为274 kN时，球台受拉侧管壁向球台受压侧弯曲，球台底部焊缝裂缝变大；最终当荷载为289 kN 时，球台底部裂缝迅速贯通，停止试验.JD-4 发生球台处母材屈曲-撕裂破坏.加载初期无明显现象；当荷载为297 kN时，螺栓球向拉杆方向上转动，此时球台受拉侧焊缝开裂；当荷载为320 kN 时，球台受拉侧管壁向球台受压侧弯曲，螺栓球与受压侧球台内壁发生挤压并发出较响的金属碰撞声，此时裂缝向球台管壁上发展；最终当荷载为369 kN 时，球台受拉侧被撕裂、受压侧弯曲失稳，停止试验.

图3 试件破坏形态Fig.3 Failure shape of specimens

综上，法兰盘球型分支节点的破坏模式均表现为高强螺栓剪切破坏，这是因为其腹杆合力点位于外螺栓球，易发生偏心受力，且附加弯矩较大，进而导致试件在外螺栓球和套筒之间的高强螺栓持续受剪被剪断.法兰盘螺栓球节点的破坏模式为球台焊缝撕裂破坏和母材屈曲-撕裂破坏.当h较小b较大时，试件易发生球台焊缝撕裂破坏；当h较大，b较小时，试件易发生球台处母材屈曲-撕裂破坏.这是因为h增大，提高了球台的纵向刚度，但由于b的减小，球台的横向刚度降低，此时球台呈“长细型”，进而发生失稳-撕裂破坏.

3 试验结果及其分析

3.1 法兰盘等效应力分析

法兰盘主要作用是防止内螺栓球脱落，主要承受拉力和由于球偏转而带来的挤压作用，为该2 种节点的重要部件，所以分析2 种节点法兰盘的等效应力分布情况.法兰盘测点分布情况见图4，不同载荷下的等效应力分布曲线见图5.

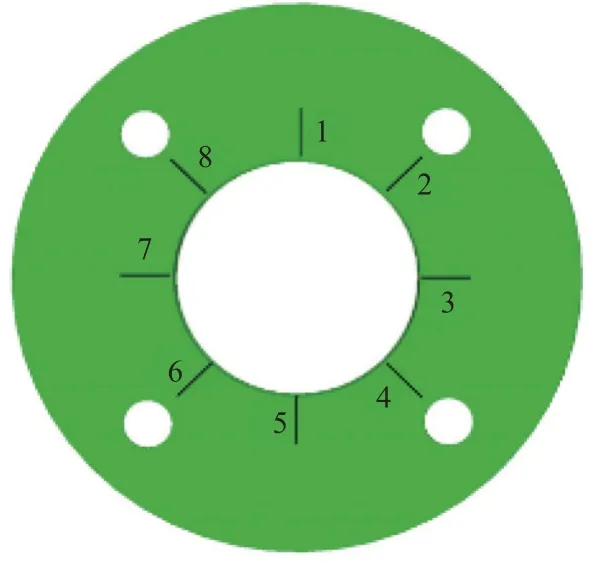
图4 法兰盘应变花编号Fig.4 Flange strain rosette number

图5 法兰盘等效应力分布Fig.5 Equivalent stress distribution of flange

由图5（a）可知：JD-1 在加载初期，整体应力分布曲线波动较小；当加载至40 kN 时，测点5、6 的等效应力增幅明显，测点8 的等效应力次之，其余测点的等效应力增幅较缓，这是由于外螺栓球的偏心作用导致连接杆倾斜，进而对法兰盘产生挤压作用，造成测点5、6 产生应力集中现象；随着偏心程度的增加，内螺栓球受到倾斜的拉力并挤压法兰盘，进而法兰盘对其产生反作用力，使得测点8 的等效应力增长幅度跃升；当JD-1 加载至80 kN 时，最大应力在测点6，高达342 MPa，最小值在3 号测点，仅15 MPa，等效应力极差为23 倍.由图5（b）可知：当JD-2 加载至100 kN 时，最大应力在测点6，高达367 MPa，最小值在1 号测点，为55 MPa，等效应力极差为7 倍；比JD-1 的极差小且承载力提高了25%，这是由于球台高度的增加降低了连接杆对构件的偏心作用；但在加载过程中，等效应力曲线分布仍不均匀，这是由于腹杆合力点离球台核心区较远，连接杆仍存在部分初始偏心.由图5（c）可知：JD-3 在每级荷载作用下的应力分布曲线大致相似，当荷载加载至270 kN 时，最大应力在测点4，高达409 MPa，最小值在测点5，为56 MPa，等效应力极差为7 倍；与JD-1 相比，最大应力绝对值提高了20%，极差下降了70%；8 个测点一半受拉一半受压，拉、压相互抵消，整体受力较好，故等效应力曲线增长较为平稳，这是因为法兰盘螺栓球节点在加载过程中不会出现较大的转动，进而产生的偏心力小.由图5（d）可知：当JD-4 加载至350 kN 时，最大应力在测点4，高达432 MPa，最小值在测点1，为67 MPa，等效应力极差为6 倍；与JD-2 相比，最大应力绝对值提高了18%，极差下降了14%；JD-4 比JD-3 法兰盘等效应力分布更加均匀，材料利用率更好，且承载力提高了30%，这是因为球台高度的增加减缓了初始偏心和附加弯矩对内螺栓球的转动作用.

综上，在进行试验时2 种节点的内螺栓球均未被拉出，说明法兰盘能够防止内螺栓球脱落.对比2 种节点，法兰盘螺栓球节点的等效应力分布曲线优于法兰盘球型分支节点，极差较小，最大应力绝对值较大，说明前者的等效应力分布均匀，材料利用率高，承载能力强.增加球台的高度，2 种节点的承载力均显著提升，在相同荷载作用下，等效应力分布曲线更均匀，节点整体表现得更加稳定.

3.2 球台区等效应力分析

球台区为2 种节点的主要部件，同时也是薄弱部位，且在球台底部存在大量焊缝，易产生应力集中，所以分析2 种节点球台区的等效应力分布情况.球台区测点分布情况见图6，不同载荷下的等效应力分布曲线见图7.

图6 球台区应变花编号Fig.6 Number of strain rosettes in table area

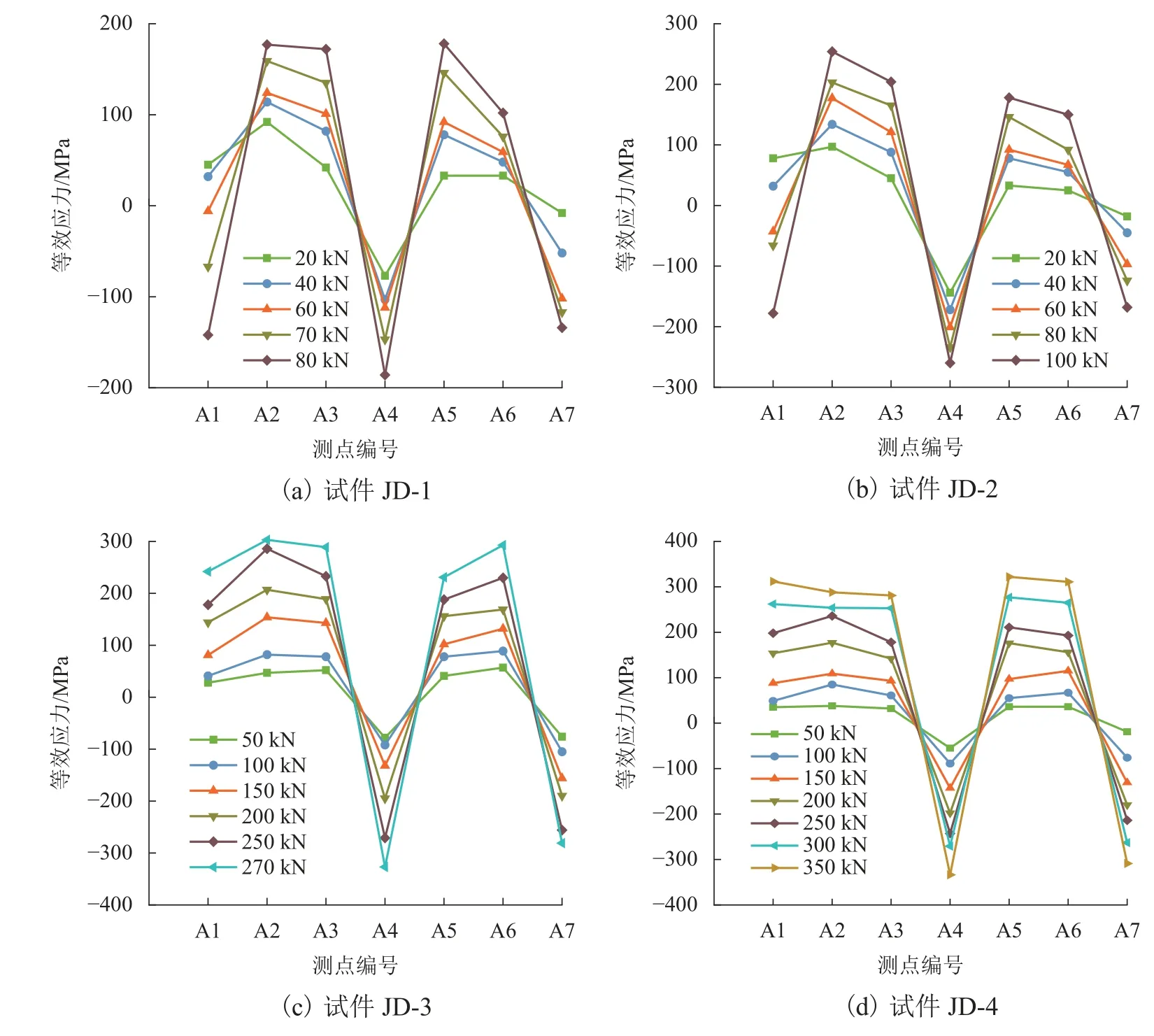
图7 球台区等效应力分布Fig.7 Equivalent stress distribution in table area

由图7（a）可知：JD-1 在加载初期，整体应力分布曲线波动较小；随着荷载的增加，测点A1 的等效应力由压力逐渐转为拉力，且增幅也越来越大，原因是加载初期内螺栓球受拉对球台产生传递拉力，后随着荷载的增加连接杆的偏心越来越大，进而对球台产生压应力；测点A7 的等效应力增幅先增加后减小，原因是加载后期连接杆和内螺栓球与法兰盘发生挤压，对球台底部的压力较小；其他测点的等效应力增长相对平稳；当JD-1 加载至80 kN 时，最大应力在测点A4，为186 MPa，最小值在测点A6，为102 MPa，等效应力极差为1.8 倍.由图7（b）可知：当JD-2 加载至100 kN 时，最大应力值在测点A4，为260 MPa，最小值在测点A6，为150 MPa，等效应力极差为1.7 倍；与JD-1 相比，极差略小，原因是球台高度的增加，减小了偏心对节点的整体影响，故等效应力曲线整体趋势较平稳.由图7（c）可知：当JD-3 加载至270 kN 时，最大应力在测点A4，为327 MPa，最小值在测点A5，为231 MPa，等效应力极差为1.4 倍；与JD-1 相比，最大应力绝对值提高了76%，极差下降了22%.由图7（d）可知：JD-4 在加载过程中，整体的应力分布曲线增幅较平缓，各测点的应力没有出现明显的波动；当JD-4 加载至350 kN 时，最大应力在测点A4，为334 MPa，最小值在测点A3，为281 MPa，等效应力极差为1.2 倍；与JD-2 相比，最大应力绝对值提高了28%，极差下降了29%；相比JD-3 的应力分布曲线更为均匀，受力情况更好，原因是球台高度的变化，使得球台外的约束刚度好，进而球体没有产生较大的转动，可以更好地传力，没有出现应力集中现象.

综上，2 种节点的最大应力绝对值均在测点A4，说明测点A4 所在的球台受挤压侧为球台的高应力区.对比2 种节点，法兰盘螺栓球节点的球台区最大应力绝对值比法兰盘球型分支节点平均提高了52%，承载能力更强.因为前者的传力路径比后者简单、明了，产生的偏心力和附加弯矩小，腹杆合力点交于球台核心区，球台平面外的约束刚度更高.球台高度由50 mm 增至60 mm 时，球台厚度由11 mm 降至7 mm，2 种节点的最大应力绝对值显著提升，应力极差明显下降，说明球台高度的增加对2 种节点的承载能力和材料整体利用率的提高起主要作用，节点对厚度的变化不太敏感.可见，球台高度为主要影响因素，厚度为次要影响因素.

3.3 腹杆轴力-变形关系

腹杆轴力-变形关系如图8.规定腹杆受拉为正，受压为负.由图8（a）可知：1）JD-1 在加载初期，曲线呈直线增长；当压力达到19 kN 时，曲线出现拐点，这是因为外螺栓球开始偏转使腹杆发生偏移，导致腹杆偏心受力产生附加弯矩所造成的；随着荷载的增加，曲线斜率有所下降；当压力达到70 kN，拉力达到75 kN 时，曲线进入塑性阶段；最终当压力为89 kN 时，试件破坏.2）JD-2 在加载初期，曲线呈直线增长；当拉力达到29 kN 时，受拉侧曲线出现拐点，此时外螺栓球产生初始程度偏心；当压力达到99 kN，拉力达到95 kN 时，曲线进入塑性阶段；最终当压力为112 kN，拉力为103 kN 时，试件破坏.由图8（b）可知：1）JD-3 在初始加载阶段曲线呈直线增长；当压力为145 kN，拉力为156 kN 时，曲线出现拐点，斜率有所下降，曲线进入弹塑性阶段；当压力为255 kN，拉力为220 kN 时，曲线进入塑性阶段；最终当压力为289 kN，拉力为275 kN 时，试件破坏.2）JD-4 在初始加载阶段曲线呈直线增长；当压力为150 kN，拉力为175 kN 时，曲线出现拐点，斜率稍有下降，曲线进入弹塑性阶段；当压力为330 kN，拉力为325 kN 时，曲线进入塑性阶段；最终当压力为369 kN，拉力为350 kN 时，试件破坏.

图8 腹杆轴力-变形曲线Fig.8 Axial force-deformation curves of web rod

综上，法兰盘螺栓球节点比法兰盘球型分支节点的承载力分别提高了225%、229%，原因是2 种节点的腹杆合力点不同，前者的合力点交于内螺栓球，在加载过程中不存在初始偏心，试件整体利用率较高，拉、压腹杆变形较为协调，同时腹杆轴力-变形曲线均趋于弧形，塑性发展阶段较长，延性较好.而后者因合力点交于外螺栓球，存在不规则不同程度的偏心，易发生脆性破坏.增加球台的高度，2 种节点的整体承载力都得到了显著的提高.

4 有限元分析

4.1 本构关系和界面处理

螺栓球使用Gardner 提出的本构关系模型，其余钢材部件和混凝土分别使用韩林海[16]提出的二次塑流模型和混凝土应力-应变关系模型.核心混凝土采用C3D8R 划分网格，螺栓球因其造型特殊故采用C3D10 划分网格，其余钢材部件采用C3D8I 划分网格.塔柱与混凝土之间，球台与螺栓球之间均使用“硬接触”和“罚摩擦”来模拟界面接触，其余构件的连接均使用Tie 绑定.塔柱两端采用固接和定向铰接约束，拉杆采用铰接约束，压杆采用定向铰接约束.

4.2 分析结果校验

有限元模拟与试验对比见图9，由图可知，试件模拟与试验破坏现象一致，两者的高应力区吻合良好，说明有限元分析的结果参考价值比较合理、可靠.节点承载力见表3，由表3 可知，模拟值与试验值相差不多，误差均在10%以内.

表3 节点承载力Tab.3 Joint bearing capacity

图9 有限元模拟与试验对比Fig.9 Comparison of finite element simulation and experiment

以上产生误差是因为在试件加工时难免会产生焊接残余应力等问题，而在有限元建模过程中材料属性等均按照理想情况设置可避免这些问题.总体来说，有限元分析与试验结果基本吻合，可进一步对球式节点进行参数拓展分析.

4.3 参数拓展分析

由于实际试验试件的数量和参数变化范围太少，故使用ABAQUS 软件进行参数拓展分析，并研究由于球台高度和厚度的变化对节点极限承载力的影响.拓展参数见表4.表中：Nuf1为法兰盘球型分支节点的极限承载力；Nuf2为法兰盘螺栓球节点的极限承载力.

表4 参数拓展结果Tab.4 Parameter expansion results

4.3.1 球台高度、厚度对Nuf1的影响分析

法兰盘球型分支节点的极限承载力与球台高度、厚度曲面拟合投影见图10.由图可知：曲面坡底（即b=6～9 mm 和h=50～55 mm 交汇面）坡度较陡峭，形成的投影等高线较密实，承载力增幅较大；在b=9～12 mm 和h=55～62 mm 形成曲面的坡度逐渐放缓，尤其坡顶曲面明显变得平缓，承载力增幅变缓.

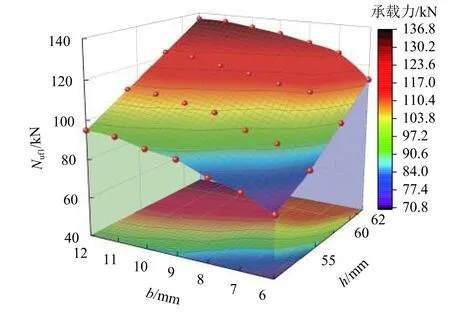
图10 Nuf1 与h、b 曲面拟合投影Fig.10 Nuf1,h,and b surface fitting projection diagram

综上所述，在h、b共同分析时，Nuf1随着h、b的增加，增幅呈现先上升后下降的趋势.从投影等高线的疏密程度看，球台高度一侧的等高线始终比球台厚度一侧的等高线稠密，即增加法兰盘球型分支节点的球台高度比增加球台厚度对其承载力的提高效果更好.这是因为此种节点的腹杆合力点交于外螺栓球，离球台核心区较远，受力适应性较差，增加球台的高度，相当于缩短了合力点到球台核心区的距离，缓解了偏心力的作用，大大提高承载力，但球台厚度的增加改变不了合力点到球台核心区的距离，对承载力的提高贡献相对较小.

4.3.2 球台高度、厚度对Nuf2的影响分析

法兰盘螺栓球节点的极限承载力与球台高度、厚度曲面拟合投影见图11.由图可知：曲面坡底（即b=6～9 mm 和h=50～55 mm 交汇面）坡度较平缓，形成的投影等高线较稀疏，承载力增加缓慢；在b=9～11 mm 和h=55～60 mm 形成曲面的坡度逐渐抬升，坡度陡峭，投影等高线较密实，承载力增加较快；在b=11～12 mm 和h=60～62 mm 形成曲面的坡度明显放缓，坡顶比较平缓，承载力增加幅度变缓.

图11 Nuf2 与h、b 曲面拟合投影Fig.11 Nuf2,h,and b surface fitting projection diagram

综上所述：1）在h、b共同分析时，Nuf2随着h、b的增加，增幅呈现先上升后下降的趋势，从投影等高线的疏密程度来看，当前期h、b均较小时，球台高度的增加比厚度的增加对承载力的提高幅度大，当后期h、b均较大时，球台厚度的增加比高度的增加对承载力的提高幅度大.这是因为前期随着球台高度的增加，相对减小了腹杆合力点到球台核心区的距离，缓解了偏心力的作用，但是后期由于球台高度太高，会造成球台屈曲失稳.2）前期承载力随着厚度的增加提高不明显，但是后期随着厚度的增加，大大地提高了球台的平面外刚度，球台不至于早早地破坏，节点承载力得到了提高.

对比图10 与图11 可知：图11 的整体曲面高度始终高于图10，说明法兰盘螺栓球节点的承载能力比法兰盘球型分支节点的好；并且后者的曲面多皱褶，凹凸不平，落差较大，前者曲面较光滑，等高线分布较均匀，说明球台高度或厚度的变化，对后者承载力的提高效果更好.