砂土拱效应滑移面几何轮廓与松动土压力分析
2023-12-21周思危冷伍明聂如松李亚峰狄宏规陈伟庚
周思危 ,冷伍明 ,2,3,聂如松 ,2,3,李亚峰 ,狄宏规 ,陈伟庚
(1.中南大学土木工程学院,湖南 长沙 410075;2.中南大学重载铁路工程结构教育部重点实验室,湖南 长沙 410075;3.中南大学高速铁路建造技术国家工程实验室,湖南 长沙 410075;4.同济大学道路与交通工程教育部重点实验室,上海 201804;5.中国铁路广州局集团有限公司,广州 510088)
土拱效应是广泛存在的自然现象,是由于土颗粒介质的不均匀位移而导致在土体中表现出的一种应力重分布效应.土拱效应普遍存在于桩承式路堤、山体抗滑桩、隧道与基坑开挖以及挡土构筑物等岩土及地下工程领域.Terzaghi[1]在1943 年通过Trapdoor试验揭示了这一现象的存在,观测到了土体内部出现的滑裂面,并提出了作用在活动门上的松动土压力计算方法.此后迄今,Trapdoor 试验作为经典且实用的力学试验,一直备受国内外土拱效应研究的广泛应用和密切关注.
国内外学者基于Trapdoor 试验或其改进装置,针对填料内部的滑移面形态与活动门上土压力的分布及变化等特征开展了丰富研究.滑移面形态的发展与土体破坏模式是拱效应的宏观表现,结合先进测试手段,国内外众多模型试验对其开展了全面的观测和分析.Costa 等[2-3]通过离心机Trapdoor 试验研究滑移面形态在不同重力场和砂密度条件下的变化发现:随着活动门下移,滑移面形态经历弧形—三角形—竖直面的演变过程;离心加速度越高,砂密度越小,滑移面水平夹角越大;随着X 射线、CT 扫描及PIV(粒子图像测速)等观测技术的发展,滑移面形态被更精确地采集.Rui 等[4]自制多沉陷门试验装置,利用PIV 技术观测砂土中滑移面的演变过程,发现在低填土中滑移面由三角形演变为竖直面,高填土中滑移面由三角形变为烟囱形再变为竖直面.Eskisar 等[5]利用CT 扫描技术对三维模型试验中“拱结构”形态进行观测,发现“拱结构”形态近似为楔形体,且楔形体高度随填料内摩擦角的增加而减小.土拱效应在砂土等细粒料中直观表现为滑移面,而在粗粒料中通常形成塌落拱结构,为此,不少学者选用球珠颗粒替代土以探明自承拱结构的形态及稳定特性.Hong 等[6]和Ahmadi 等[7]分别研究砾石和球珠材料在活动门下移过程中“稳定拱”的形成及演化发现,“稳定拱”形状为半圆环形(2D)或穹顶形(3D),稳定拱跨为0.75 倍~1.15 倍活动门宽度,且砾石填料的拱跨远大于球珠填料的拱跨.目前,关于滑移面形态及演化规律等研究结论虽存在相似[2,4,6,8-11],但由于试验装置、观测手段和填料种类有所差别,造成滑移面高度、宽度和夹角等具体几何轮廓存在较大的区别[2,5,12-17],尚未形成一致性示例以准确描述滑移面的延展路径,同时缺乏适用的几何特征参数以全面掌握滑移面的几何轮廓信息.
活动门上的松动土压力直接反映应力转移的多少,体现土拱效应的发挥程度.国内外学者同样基于Trapdoor 试验对松动土压力开展了一系列研究.Chevalier 等[11]和Dewoolkar 等[12]均对活动门上的松动应力随活动门下移的变化规律进行研究发现,松动应力-活动门下移曲线可分为衰减、恢复与稳定3 段,并且恢复段应力-位移曲线呈线性.Iglesia 等[3]针对曲线的衰减段进行研究发现,填土越高,活动门宽度越小,应力衰减越多.Han 等[13]将该曲线近似简化为三段直线,并提出简化曲线由最大、最小拱来确定.通过对比试验结果及国内外研究结论,验证了简化曲线的可靠性.目前研究所得的松动应力-活动门下移曲线特征类似[3,12,15,17-22],但对该曲线的衰减、恢复段斜率、稳定段长度以及最大、最小拱状态下的松动应力和活动门下移等曲线特征的变化规律犹未可知.
本文基于Trapdoor 试验深入研究滑移面几何轮廓特征以及松动应力-活动门下移曲线特征.通过指定滑移面轮廓特征参数获得轮廓特征在土层中的分布以及随活动门下移的变化规律,利用滑移面几何轮廓信息界定土体内部松动区范围及松动区形态演变模式,并提出考虑松动区形态演变的松动土压力计算方法.通过指定松动应力-活动门下移曲线特征参数获得最大、最小拱状态下的松动应力随填土高度和内摩擦角的变化规律.将松动土压力改进算法与试验结果以及国内外研究成果进行对比,验证了本文改进方法的可靠性和实用性.
1 Trapdoor 模型试验
1.1 试验装置
Trapdoor 试验模型箱如图1 所示,模型箱由上部箱体和下部底座构成.上部箱体为上、下两端开口的长方体,箱体外框主骨架由角钢焊接而成,箱体四周侧面为1 cm 厚有机玻璃.下部底座由15 块钢板拼接组成,包括中心钢板(宽200 mm)与两侧条形钢板(宽50 mm),可灵活调节改变活动门与其两侧不动底座的宽度.每块钢板前、后两侧均采用螺栓与底板的前、后两端固定连接,通过螺杆控制任意一块钢板的下移,最大下移高度达100 mm.同时为确保平面应变条件,在每块条形钢板的前、后两侧均固定有高100 mm 的玻璃挡土板,挡土板内壁紧贴箱体外壁,从而在活动门下移过程中对箱内填料的位移方向加以约束.

图1 Trapdoor 模型试验箱结构示意(单位:cm)Fig.1 Trapdoor test box structure(unit: cm)
在活动门与其一侧底座的中心以及活动门上方沿填料中心线等间距布置多点式薄膜(MFF)压力传感器(如图1 所示),以测试作用在活动门、不动底座上的应力以及填料各层的竖向应力.薄膜压力传感器长、宽、厚分别为51、14、0.2 mm,受力感应区为圆形,直径9.52 mm,量程10 N,精度1.2%满量程,根据标定系数由输出电压E获得压应力σ(由感应区面积转换为kPa).采用百分表测量活动门下移量,百分表量程100 mm,分度值0.01 mm,在下移钢板的前后两端各安装1 个.将光源、摄像头、支架等固定在试验箱正面,试验中同步拍摄填料变形,并获得土层位变信息.
1.2 测试方法
对试验拍摄填料变形图像进行处理分析,以获取图像中目标测试点的位置变化信息[23-25].OpenPIV是基于MATLAB 和C++语言的开源程序,在物体瞬态位移及运动轨迹追踪等摄影测量技术领域得到了广泛应用[23].其基本原理:通过将一系列连续拍摄的瞬时图像依次导入程序,根据图像中色彩纹理及光散射率特性的不同,采集图像中目标测试点的坐标并识别相邻图像测试点坐标的变化;通过图像区块相关性匹配输出全场速度和位移矢量;根据图像与原型之间的比例转换得到实际的速度和位移,从而实现图像中任意点位置变化的实时监测.
测试过程中,将图像导入OpenPIV[23]后设置界面图幅大小,图幅像素范围4~256 像素,为满足数据采集鲁棒性的同时确保较高的分辨率,本试验选取32 像素 × 32 像素.同时,利用OpenPIV 界面的局部图像分析模块(ROI)加密布置分析区域内的测点,以实现局部范围内数据的重点采集分析.程序运行后得到各测点的水平和竖向速度矢量,单位像素/s,与相邻图像拍摄的时间间隔t(s)及比例尺(m/像素)相乘即可得到位移矢量.
1.3 试验方案
Trapdoor 试验是一种基于理想二维条件下开展的平面应变和平面应力试验.Trapdoor 试验箱长宽比通常取4~8[10-16],在这种狭长空间内试验填料与箱体内壁的摩擦将会破坏理想平面状态,显著影响试验结果.因此,需测定和严格要求填料的黏聚力、相对密度、内摩擦角等物力指标,通常选用黏聚力低、配位数小、流动性强的材料作为试验填料[4,7,10,17,21,22],并严格保证试验箱内壁光滑.本文选用 中值粒径d50为0.25~0.55 mm,相对密度Dr为0.200~0.850 的粗、中、细3 种洁净干砂开展Trapdoor 试验,3 种干砂的颗粒级配曲线如图2所示,经测试获得3 种砂的系列物理力学参数如表1 所示.针对3 种砂分别开展不同填土高度h和活动门宽度w的Trapdoor 试验,试验组工况如表2 所示.

表1 砂物理力学参数Tab.1 Physical and mechanical parameters of sand

表2 Trapdoor 试验组工况Tab.2 Trapdoor test conditions

图2 砂颗粒级配Fig.2 Grading of sand particles
试验中对砂料内滑移面的形成和延展过程进行观测,获得上述试验组各级滑移面的几何轮廓及其典型演变模式,在此基础上提出全面描述滑移面几何轮廓信息的特征参数,并获得砂料种类以及试验条件对几何特征参数的影响规律.试验结果为滑移面几何轮廓及其延展路径分类提供典型示例与指标.具体试验步骤如下:
步骤1按每层50 mm 分层填砂,层间均匀铺撒一层10 mm 厚的天然彩砂,并在预设位置埋设薄膜式压力传感器(如图1 所示);
步骤2填至预定高度后,静置待压力传感器读数稳定,记录读数并拍摄砂料照片;
步骤3缓慢下移活动门,每下移1 mm,待变形和传感器读数稳定后同步完成数据采集和拍摄.利用OpenPIV 对拍摄的砂料变形瞬时图像进行粒子图像测速(PIV)分析,依次对比活动门每下移1 mm前、后的颗粒位置、输出颗粒速度和位移矢量;
步骤4重复步骤1~3,直至彩砂条带破坏或箱体底部出现坍砂时结束试验.
疼痛可以直接影响到病人的生活质量,疼痛发作时,机体会出现一系列地病理和生理反应,同时会让患者主观出现不悦的感受,在心理上给患者造成了巨大的困扰,而这些因素又恰恰决定着化疗、放疗及相关的一些治疗能否继续进行。[3]疼痛是一些晚期癌症病人常见的临床表现,尤其是持久、强烈、无法忍受的疼痛,这些会经常引起一系列症状,如食欲发聩、睡眠不佳、焦虑、烦躁、忧郁、甚至消极抗拒治疗等等,从而使得病情恶化。因而改善患者的疼痛状况,缓解情绪反应至关重要。我们需要加强对患者疼痛方面的教育,使晚期癌症患者度过舒服、平静的终末期。
2 试验结果分析
2.1 滑移面几何轮廓特征
将各层彩砂变形曲线的拐点自下而上依次连接,得到从活动门两侧边缘向砂内部延伸的滑移面.为研究不同砂料种类和试验条件下典型滑移面轮廓及其一般性的演变模式,选取高宽比h/w=3 的粗砂与高宽比h/w=2 的细砂试验组进行对比观测,如图3所示,ΔS为滑移面轮廓随活动门下移位移.

图3 滑移面轮廓典型演变模式Fig.3 Typical evolution modes of slip surface contour
由图3 可知:ΔS/w的演变过程为三角形—子弹头形—椭圆形,与Rui 等[4]“初始三角拱”及“烟囱形滑移面”结论相似;对于高宽比h/w=2 的细砂试验组,初始三角形滑移面随活动门下移表现为“顶部上升、两侧扩展”的演变特征,同Rui 等[4]的“三角扩展型滑移面”结论相合;对于高宽比h/w=3 的粗砂试验组,初始滑移面形成后即保持稳定,随活动门下移基本不再变化.
将各组最终形成的完整滑移面进行比较,通过OpenPIV 中的局部图像布点功能(ROI),按照砂料分层厚度将图像分解为若干层,分别采集获得各层彩砂测点的颗粒位移场,如图4 所示.由图4 可得:初始、次级滑移面均随填土高度的增加和活动门宽度的减小而愈发尖锐,当填土高度足够高时,“子弹头”下部近似呈竖直面(如图4(d)所示).

图4 滑移面典型轮廓及其等值线(粗砂,Dr=0.860)Fig.4 Typical contours of slip surface and its contour line(coarse sand,Dr=0.860)
第Ⅲ级滑移面随活动门下移不断向上延伸,在低填土试验组中延伸至顶面并交于表面沉陷槽两侧边缘,在高填土内则形成完整椭圆形闭合圈,且活动门越宽,闭合圈面积越大,如图5 所示,图中:hs1、hs2、hs3和hs31分别为初始、次级、第Ⅲ级滑移面高度和第Ⅲ级滑移面拐点高度;θ1、θ2、θ31和θ32分别为初始、次级滑移面夹角和第Ⅲ级滑移面上半夹角、下半夹角.

图5 滑移面几何轮廓特征参数释义Fig.5 Interpretation of geometric contour parameters of slip surface
2.1.1 滑移面高度hs
滑移面高度hs随活动门下移的变化如图6 所示.由图可知:各试验组变化规律类似,hs随活动门下移递增;当活动门下移较小时,hs增长较缓慢,随着活动门下移的增加,hs增长速率先增大,后减小,再增大,最终趋缓,分别对应于初始滑移面形成、次级滑移面形成、滑移面稳定阶段、第Ⅲ级滑移面形成以及滑移面破坏阶段;高宽比和密度越大,曲线第一阶段增长越缓慢,第二、三阶段增长越显著,反映初始滑移面形成过程较长,次级、第Ⅲ级滑移面随活动门下移的演化程度相对更高.
第Ⅲ级滑移面椭圆拐点处填土高度随活动门下移的变化如图7 所示.由图7 可知:hs31为填土高度的0.1 倍~0.7 倍;hs31随活动门下移递减,填土越高,密度越小,hs31变化幅度越大.

图7 第Ⅲ级滑移面拐点高度随活动门下移变化Fig.7 Change of inflection point height of level-Ⅲ slip surface with downward movement of trapdoor
各试验组(h=0.4 m 与h=0.6 m)完全形成的初始、次级、第Ⅲ级滑移面高度,如表3 所示.由表可知:各试验组变化规律类似,初始滑移面高度hs1在填土高度的0.2 倍范围内变化,填土高度越高,活动门越宽,hs1越大;次级滑移面高度hs2为填土高度的0.3 倍~1.0 倍,hs2随高宽比与内摩擦角的增加而增大;试验组中,第Ⅲ级滑移面延至填土表面,故hs3稳定在填土高度保持不变,对于未延至表面的试验组,hs3为0.5 倍~1.0 倍填土高度;hs3与填土高度呈正相关,与内摩擦角呈负相关;第Ⅲ级滑移面拐点高度hs31为填土高度的0.1 倍~0.5 倍,hs31随内摩擦角近似线性递增.

表3 稳定滑移面高度-内摩擦角Tab.3 Stable slip surface height-internal friction angle m
2.1.2 滑移面夹角θi
滑移面夹角随活动门下移的变化曲线如图8 所示.由于各级滑移面左右两侧夹角相近,故取平均值进行统计和分析.由图可得:初始、次级滑移面夹角随活动门下移均先增后减,其中,初始滑移面夹角θ1在65°~83° 内变化,次级滑移面夹角θ2为74°~90°,两者均介于(45°+φ/2)~90°,同Costa 等[2]75°~85°以及Rui 等[4]67°~78° 试验结果相符;θ1的变化幅值小于θ2,且在θ2的变化过程中θ1基本不变,表明初始滑移面稳定性更高,θ1、θ2均同填土高度呈正相关,同活动门宽度及内摩擦角呈负相关;填土高度的影响更显著,当h=0.4 m 增至1.2 m,θ1、θ2分别增长了21.56%、14.47%,内摩擦角对θ2的影响较大,对θ1影响相对较小;θ31、θ32大小相近,均在80°~90° 内变化,且均随活动门下移而增大,高宽比越大,θ31、θ32越小,砂密度对θ31的影响较大,对θ32的影响较小.

图8 滑移面夹角随活动门下移的变化Fig.8 Change of angles of slip surface with downward movement of trapdoor
2.1.3 松动核心区形态
θ2与θ31沿土层自下而上逐渐减小,减小至θ1时对应的填土高度定义为等斜率填土高度hd.将连接活动门两侧边缘与hd同次级或第Ⅲ级滑移面两侧交点构成的四边形作为活动门上方松动核心区域,如图9 中区域ABCD所示.图9 中:ψ(区域ABCD两侧底角)为松动核心区水平夹角;SAEFD为竖直面松动区面积;Acor(区域ABCD面积)为松动核心区面积.
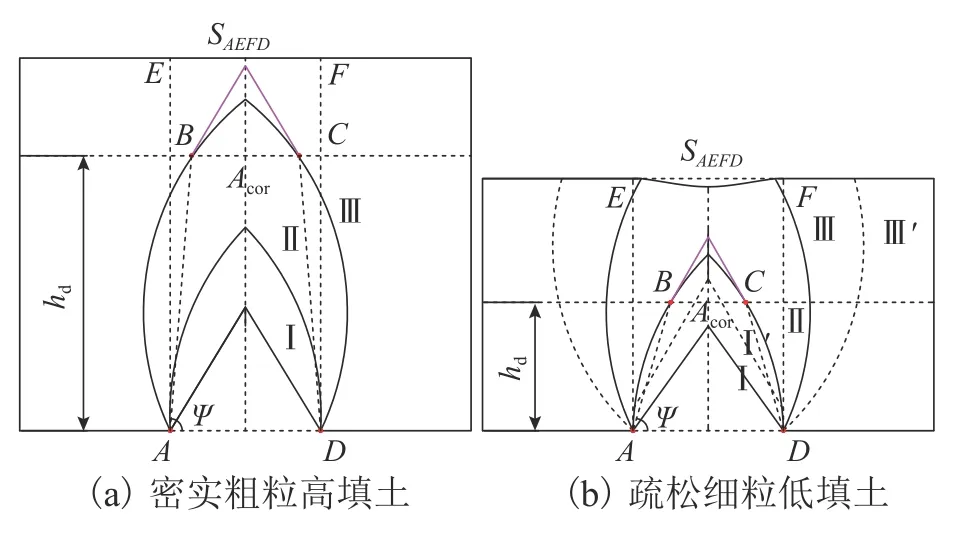
图9 2 类典型试验组中松动核心区形态Fig.9 Morphology of core loosening zones in two types of typical test groups
统计各试验组中上述几何参数随内摩擦角的变化,如表4.由表4 可知:hd为填土高度的0.5 倍~0.8 倍,填土高度越高,hd越大;内摩擦角越大,hd越小,ψ随内摩擦角的增加而减小,低填土试验组(h=0.4 m,h=0.6 m)中ψ为80.0°~85.0°,高填土试验组(h=0.8 m,h=1.2 m)中ψ为87.5°~90.0°,随着填土高度的增加,核心区形态由三角形演变为梯形或矩形;Acor/SAEFD同内摩擦角近似呈线性负相关.
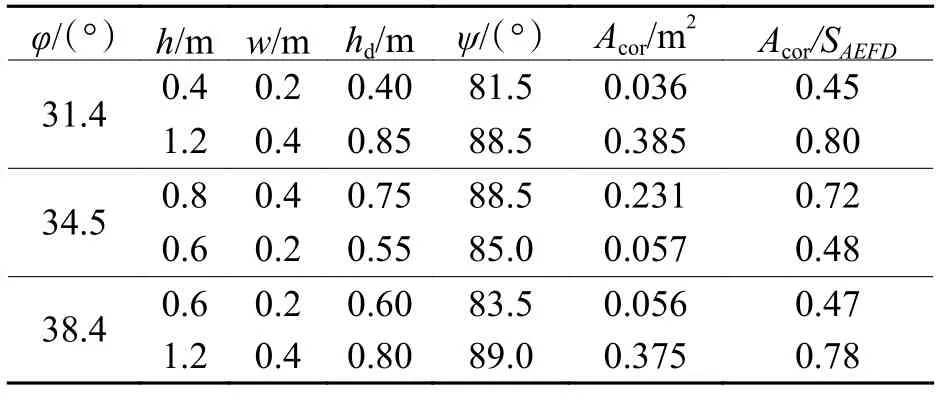
表4 松动核心区几何特征Tab.4 Geometric characteristics of core loosening area
2.2 松动应力-活动门下移曲线特征
采集活动门上的应力(传感器1# 读数)随活动门下移的变化,如图10 所示,图中,σ0为初始应力.经分析可知,各试验组变化规律类似,随着活动门下移,应力变化过程可分为衰减、恢复和稳定3 阶段:衰减阶段对应于初始滑移面的形成,土拱效应的发展将上覆填土荷载由活动门上方向两侧转移,导致活动门上土应力降低;恢复阶段对应次级滑移面的形成和演化,滑移面区域的扩张使得越来越多的填土荷载作用于活动门上,造成活动门应力的增长;稳定阶段对应于第Ⅲ级滑移面的形成及稳定后,活动门应力基本保持不变.试验结果同Chevalier 等[11]、Dewoolkar 等[12]所得结论相合.
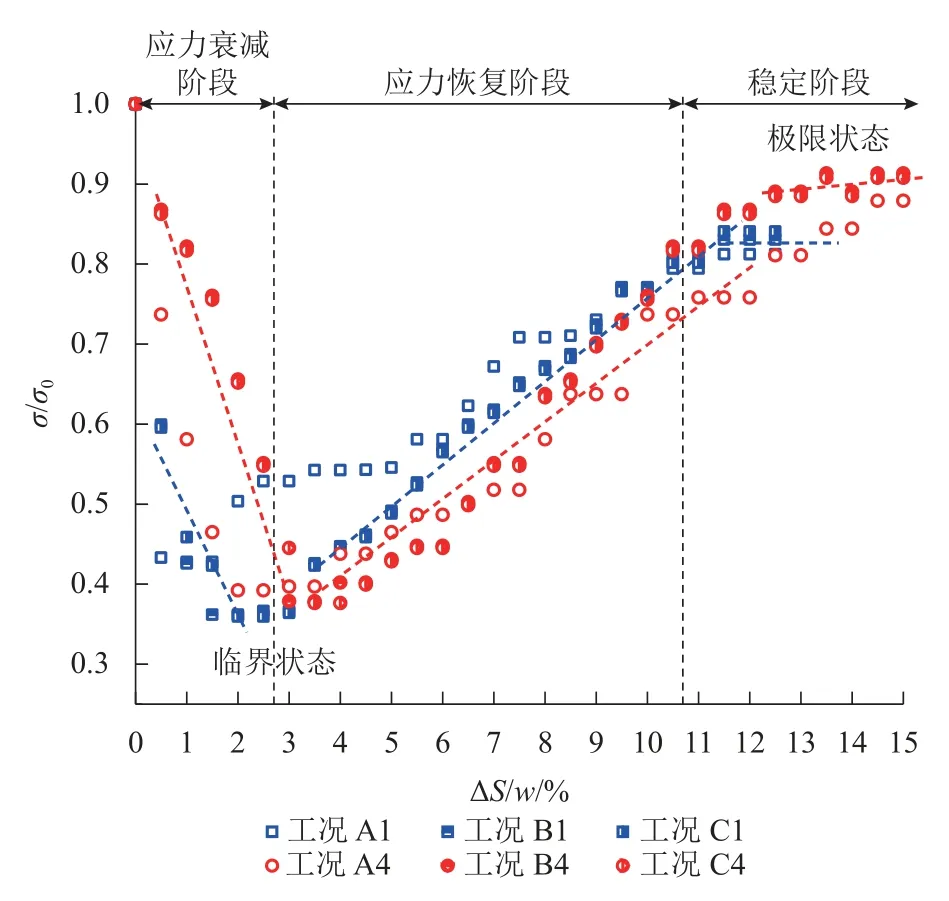
图10 松动应力-活动门下移归一化曲线Fig.10 Normalization curves of loosening stress-downward movement of trapdoor
统计各试验组曲线中临界状态(应力谷值点)、极限状态(应力稳定段起点)的应力和活动门下移量,如表5 所示,表中:σcri为临界应力;ΔScri为临界位移;σult为极限应力;ΔSult为极限位移.结果表明:σcri/σ0在0.30~0.45 内变化,高于Dewoolkar 等[12]20%的结论;高宽比和内摩擦角越大,σcri/σ0越小;ΔScri占活动门宽度的0.5%~3.5%,与Dewoolkar 等[12]1.5%的试验结果相符,高宽比和内摩擦角越大,ΔScri/w越大;σult/σ0为0.8~1.0,σult/σ0与填土高度、内摩擦角呈正相关;ΔSult/w为5.0%~15.0%,ΔSult/w随活动门宽度和内摩擦角的增加而减小,随填土高度的增加而增大.

表5 临界、极限状态特征Tab.5 Characteristics of critical and ultimate states
将活动门上应力大小近似为松动核心区域内土重,通过Acor计算松动土压力(γAcor/w),同试验结果以及Terzaghi[1]松动土压力计算结果进行对比,如图11.由图可知:低填土试验组(h=0.4 m,h=0.6 m)中,核心区Acor计算结果与Terzaghi[1]计算方法所得应力大小同试验实测临界应力大小相近;高填土试验组(h=0.8 m,h=1.2 m)中Acor计算结果同实测极限应力大小相近,Terzaghi[1]计算误差相对较大.利用Acor计算松动应力的改进算法相比Terzaghi[1]基于竖直破坏面的应力计算方法具有更好的适用性.当填土高度较低时,核心区形态近似三角形,改进算法适用于计算临界应力;当填土高度较高时,核心区形态为四边形,改进算法适用于计算极限应力.
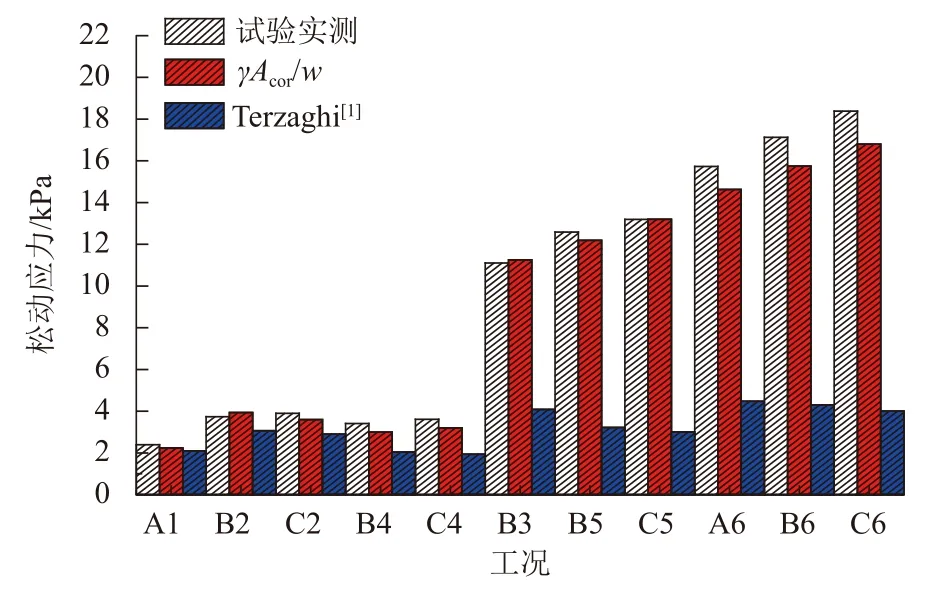
图11 松动应力计算方法对比Fig.11 Comparison of loosening stress calculation methods
将试验结果与Chevalier 等[11]松动应力-活动门下移近似计算结果进行比较,如图12 所示.由图可知,应力衰减阶段与恢复阶段,Chevalier 等[11]计算结果均与试验结果接近.Chevalier 等[11]采用三角形滑移面区域面积SΔ计算恢复阶段应力(σ=γ(SΔ/w×ΔS)),利用表4 中Acor替代SΔ计算出的所得应力与实测结果具有更高的吻合程度(如图12(b)),进一步验证了本文计算方法的实用性.
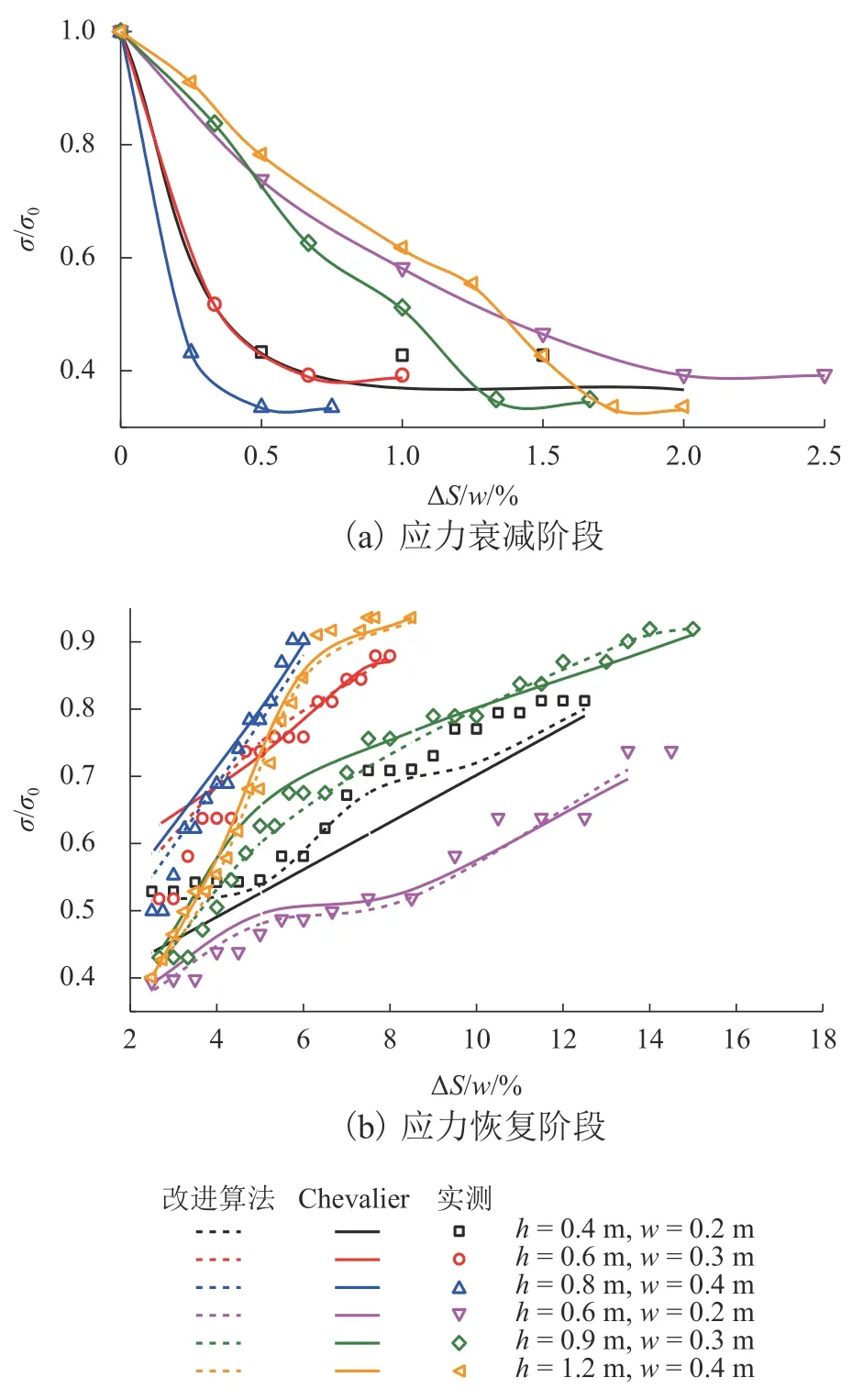
图12 松动应力-活动门下移近似计算Fig.12 Approximate calculation of loosening stressdownward movement of trapdoor
3 结论
通过Trapdoor 试验对砂土拱效应滑移面几何轮廓特征以及松动应力-活动门下移曲线特征开展了较为系统的研究.获得了填土高度、活动门下移和宽度以及砂土密度对上述特征量的影响规律.通过对松动核心区几何形态的研究,提出了考虑松动区形态演变的松动土压力计算方法.主要结论如下:
1)随着活动门下移,滑移面轮廓的演化过程为三角形—子弹头形—椭圆形.随着填土高度的增加,松动核心区形状演变过程为三角形—梯形—矩形.
2)初始、次级滑移面高度随活动门下移递增,与内摩擦角呈正相关.第Ⅲ级滑移面高度与内摩擦角呈负相关,第Ⅲ级滑移面拐点高度随活动门下移递减.大小顺序为hs31<hs1<hs2<hs3.初始、次级滑移面夹角随活动门下移先增后减,第Ⅲ级滑移面夹角随活动门下移递增,大小顺序为θ1<θ2<θ31≈θ32.
3)σcri/σ0∈(0.3,0.45);ΔScri/w∈(0.5%,3.5%);σult/σ0∈(0.8,1.0);ΔScri/w∈(5.0%,15.0%).填土高度越高,内摩擦角越大,临界应力越小,临界位移越大.极限应力与极限位移同填土高度呈正相关,同活动门宽度呈负相关.
4)松动核心区高度为填土高度的0.5 倍~0.8 倍,松动核心区夹角与松动核心区面积随内摩擦角的增加近似线性递减.相比Terzaghi 土柱理论和Chevalier等近似计算,利用Acor的松动土压力计算方法与试验结果更吻合.
