纵筋率对UHPC 华夫桥面单向板抗弯承载力的影响
2023-12-21刘振伦陈可道
张 锐 ,赵 冉 ,刘振伦 ,胡 棚 ,陈可道 ,李 晰
(1.西南交通大学土木工程学院,四川 成都 610031;2.青岛理工大学土木工程学院,山东 青岛 266525)
钢-混凝土组合梁桥是在钢结构和混凝土结构基础上发展起来的一种新型结构形式.该类型桥梁主要通过在钢梁和混凝土板之间设置剪力连接件抵抗界面处的剪力与相对滑移,从而使两者成为共同工作的整体[1].由于钢-混组合梁桥充分利用了钢材与混凝土的力学性能,使两者的性能得到了充分发挥,因而可以显著降低结构高度、提高刚度[1].但由于传统的混凝土桥面板易开裂,桥面有害物质可通过桥面板裂缝侵入主梁造成锈蚀,从而严重影响钢-混凝土组合桥梁的耐久性及其应用范围[2].
超高性能混凝土(UHPC)是20 世纪70 年代兴起的一种具有高强与高耐久性的新型纤维增强水泥基复合材料.与普通混凝土不同,一定体积量的钢纤维被加入到UHPC 基体中用于增韧[3],从而使UHPC在单轴拉伸荷载作用下具有一定的应变硬化现象,且UHPC抗压强度较高,其立方体抗压强度不低于150 MPa,直接拉伸强度不小于5 MPa[4].由于UHPC基于最大堆积理论进行材料设计[5],其本身水胶比较低,因此,UHPC 的密实度较高,渗透率极低,具有超高耐久性[6].因此,为解决普通钢-混结构组合梁桥中遇到的易开裂和承载力不足等问题,UHPC 被首先应用于桥面加固[7].后来有学者提出了钢-UHPC华夫桥面板组合桥的概念,并进行了初步设计、理论和试验研究[8-9].随着钢-UHPC 华夫桥面板展现出了轻质、高强等优势后,美国联邦高速公路管理局率先颁布了《预制UHPC 华夫板设计指南》[10].Aaleti等[11]以美国爱荷华州的一座混凝土简支梁桥为试点,首次将UHPC 华夫桥面板用于替换传统混凝土桥面板,并针对不同荷载条件开展了有限元分析与试验研究.Ghasemi 等[12-13]通过对配置CFRP 筋与高强钢筋的单肋、多肋及单跨、两跨梁进行试验研究,分析了其弯曲、整体、连续及冲剪性能和荷载分布.Baghi 等[14-15]对单肋、多肋及单跨、两跨华夫板进行了精细化有限元建模,并与试验结果进行了对比.邵旭东等[16-18]提出一种适用于大跨径与中小跨径的钢-UHPC 轻型组合桥梁结构,并进行了概念设计和承载力验算.此外,还对纵横向华夫板条带及其接缝进行了试验与数值分析,证明了该结构在力学与经济方面的优越性.张清华等[19]提出了一种新型装配式UHPC 华夫板组合梁,并以某三跨连续梁桥为研究对象,建立了有限元模型并进行参数分析,提出了UHPC 华夫板的合理设计参数.朱劲松等[20]对钢-UHPC 华夫板组合梁进行了抗剪性能试验,并提出了钢-UHPC 华夫板组合梁抗剪承载力计算公式.邵旭东等[21]以实桥为背景,开展了UHPC 华夫板横向抗弯的试验与有限元研究,并基于有限元模型进行了参数分析.尽管目前针对钢-UHPC 华夫桥面板组合梁已有一些理论与试验研究,但大多未将UHPC材料性能试验、构件试验以及理论分析进行系统的结合.此外,为考虑UHPC 受拉性能对抗弯承载力的贡献,国内外学者和设计规范一般基于均匀分布系数对受拉区UHPC 的受拉应力分布等效为矩形分布.截至目前,均匀分布系数的取值存在较大差异,且未考虑纵筋率对其取值的影响.
本文为研究纵筋率对UHPC 华夫桥面单向板的抗弯性能的影响规律,分别从材料、构件和理论分析3 个层次开展研究.在材料层次,基于UHPC 材料力学性能试验提出UHPC 单轴受拉本构模型;在构件层次,开展UHPC 华夫桥面单向板简化T 梁足尺模型受弯试验;在理论分析层次,基于试验结果推导纵筋率与UHPC 受拉均匀分布系数的关系,建立UHPC 华夫桥面单向板简化T 梁受弯极限承载力计算公式,并基于既有T 型截面UHPC 梁的受弯试验结果进行验证,从而明确本研究中所提出公式的准确性.
1 材性试验
1.1 UHPC
本研究所使用的UHPC 为甘肃畅陇公路养护技术研究院提供的商品(型号UHPC-160,立方体抗压强度标准值≥160 MPa),其具体成分包含水、预拌料以及体积掺量为2%的钢纤维.其中,预拌料是由水泥、粉煤灰、硅灰、石英砂和高效减水剂按一定比例混合配制而成;钢纤维物理力学特性和UHPC 配合比分别如表1、2 所示.

表1 钢纤维特性Tab.1 Properties of steel fibers

表2 UHPC 配合比Tab.2 Mix proportion of UHPC
1.1.1 单轴拉伸性能
UHPC 的拉伸性能由单轴直接拉伸试件获得.拉伸试件具体尺寸如图1(a)所示,试件由万能试验机基于位移模式加载,加载速度为0.1 mm/min.UHPC 直接拉伸试验共加载了6 块UHPC 拉伸试件,其单轴拉伸应力-应变曲线如图1(b)所示,试验结果如表3 所示.
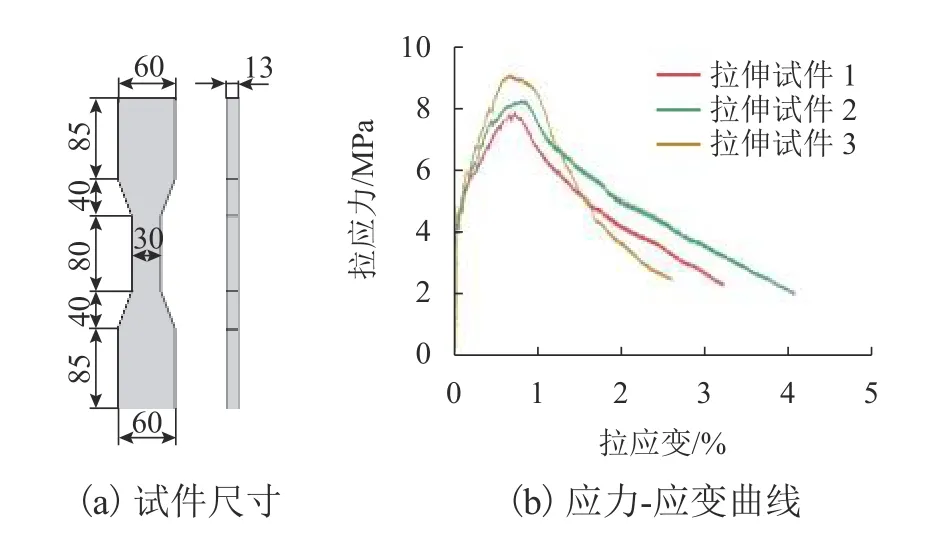
图1 UHPC 拉伸试验Fig.1 UHPC tensile tests

表3 UHPC 的单轴拉伸性能Tab.3 Uniaxial tensile behavior of UHPC
1.1.2 单轴压缩性能
为了测定UHPC 的压缩性能,分别浇筑了6 个尺寸为100 mm × 100 mm × 100 mm 立方体试件以及6 个尺寸为100 mm × 100 mm × 300 mm 的棱柱体试件.棱柱体除了用于测定UHPC 轴心抗压强度以外,还用于测量弹性模量.最终,立方体抗压强度平均值、轴心抗压强度平均值以及弹性模量平均值分别为1 660、1 418、52 GPa.可以得出,本研究所用UHPC 轴心抗压强度与立方体抗压强度之比为0.85,远大于C80 混凝土的0.63[22].这是由于UHPC中的钢纤维使UHPC 韧性较强而普通高强混凝土脆性较强.因此,基于现有规范计算得到轴心抗压强度值将显著小于实际值,从而造成UHPC 强度浪费.
1.2 钢 筋
构件底部受拉钢筋、翼缘板筋以及箍筋均采用规格为HRB400 的钢筋.其中,翼缘板筋按纵横向等间距布置,钢筋直径均为10 mm.箍筋选取了直径为6 mm 的钢筋,且按间距100 mm 进行布置.底部纵筋直径分别选取6、12、16、20、22 mm.本文所用钢筋的拉伸力学性能如表4 所示.
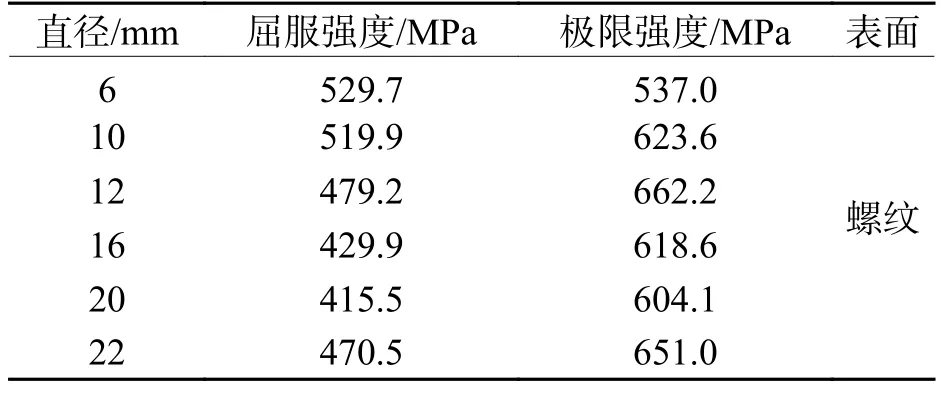
表4 钢筋的抗拉力学性能Tab.4 Tensile properties of steel bars
2 模型试验
2.1 试件设计
UHPC 华夫桥面板由顶板以及纵横向梁肋组成.本研究着眼于UHPC 华夫桥面单向板的抗弯性能,因此,基于等效宽度原理,将UHPC 华夫桥面单向板进行简化,并开展了6 根不同纵筋率T 型截面UHPC梁的四点弯曲试验,所有梁试件的翼缘板内布置了尺寸为100 mm× 100 mm 钢筋网.试验变化参数为腹板中的纵筋率,6 根试件设计参数如表5 所示,尺寸与钢筋布置如图2、3 所示.全部试件浇筑完成48 h 后拆模,然后连同材料试验试验试件放置于标准养护条件下养护28 d.
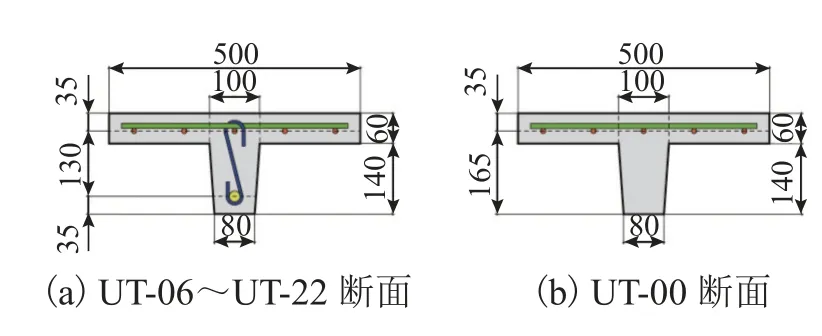
图2 试件截面Fig.2 Cross section of specimens
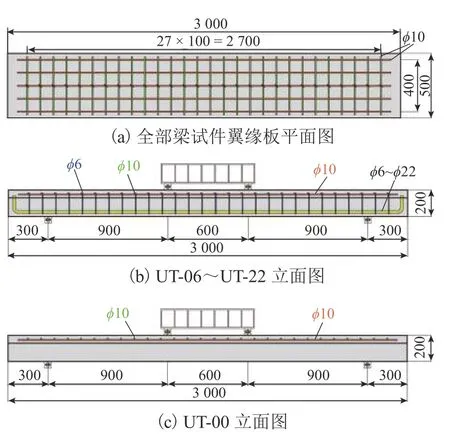
图3 试件尺寸及配筋Fig.3 Dimension and reinforcement of specimens
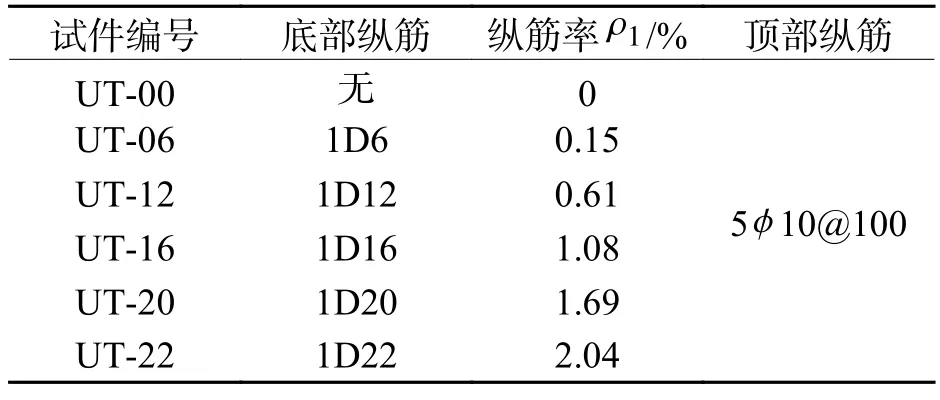
表5 试件设计参数Tab.5 Design parameters of specimens
2.2 加载与量测方案
全部T 梁的加载试验在西南交通大学土木工程实验教学示范中心完成.荷载由一台500 kN 电液伺服作动器提供.试验加载中所有T 梁跨中设置了600 mm 长的纯弯段,T 梁与分配梁均为简支.分配梁顶有荷载传感器,用于监测和记录作动器施加荷载大小.在纯弯段两侧、跨中以及支座处设置了5 个直线位移传感器(LVDT)用于测量T 梁沿跨径方向的变形情况.在跨中处沿截面高度布置混凝土应变片用于测定应变分布.试验加载装置如图4 所示.全部T 梁试件均按荷载控制方式进行恒定速度加载,加载速度为0.2 kN/s,直到T 梁进入屈服阶段并发生显著损伤或变形,然后手动停止加载并卸载.

图4 试验加载装置Fig.4 Experimental loading setup
3 试验结果
3.1 裂缝发展及破坏形态
各T 梁加载试验后的裂缝发展情况如图5 所示.试验初期,荷载线性增长,梁处于线弹性阶段;当荷载增大到一定值时,首先在跨中位置附近产生竖向裂缝;随着荷载继续增加,纯弯段内裂缝不断增多且裂缝宽度逐渐加大,裂缝开展逐渐逼近翼缘板上端,裂缝处钢纤维被拔出不断发出“嘶嘶”声,最终顶板出现垂直梁截面方向的水平裂缝而被压碎.同时,梁体下挠明显,下挠速度加快,梁承载力达到峰值后开始下降,梁体破坏.其中,UT-00 裂缝产生最少,且裂缝易集中发展,承载力最低.随着纵筋率的增加,梁体裂缝开展数量明显增多,裂缝逐渐弥散,承载力逐渐增加.最终,各T 梁均发生明显挠曲,且上缘UHPC 发生压溃,其破坏形态均为正截面受弯破坏.
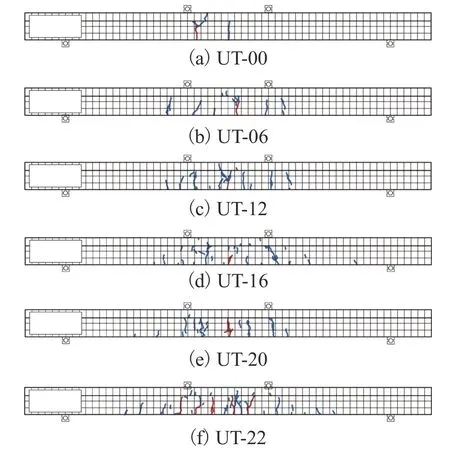
图5 加载后的裂缝分布Fig.5 Crack distribution after loading
3.2 荷载-跨中挠度曲线
各T 梁在加载过程中的荷载-跨中挠度曲线和试验结果分别如图6 和表6 所示.跨中挠度值为跨中梁底位移与支座处位移之差,荷载值为作动器处荷载传感器采集的荷载值.从试验结果可以发现:随着纵筋率增加,峰值荷载也基本呈线性增长;T 梁开裂前,随着荷载的增大,挠度呈线性增长,梁的荷载-挠度曲线为直线;开裂后随荷载增加,T 梁整体刚度逐渐下降,荷载-挠曲线的非线性特征越来越明显;当梁进入屈服阶段后期时荷载几乎不再增长,此时挠度值迅速增长,T 梁已进入破坏阶段.

图6 荷载-跨中挠度曲线Fig.6 Load-midspan deflection curves

表6 T 梁试验结果Tab.6 Results of T-shaped beam tests kN
值得注意的是,不同于钢筋混凝土(RC)受弯梁,当UT-00 在加载过程中出现第1 条裂缝后,由于裂缝处钢纤维与UHPC 的黏结作用使得构件初裂后并未发生类似于RC 无筋梁的脆性破坏.虽然该作用对梁的承载力提高不明显,但为UT-00 提供了相当的延性.此外,UT-06 的腹板虽配有纵筋,但是其纵筋率仅为0.15%,明显小于RC 结构中最小配筋率0.20%的要求[22].然而,该梁在整个受力过程中也明显表现出了适筋梁的弹性、屈服与破坏3 个阶段.可以归结为UHPC 在初裂后仍可以提供一定的拉应力,从而不会发生RC 构件中的内力重分布现象.因此,对于UHPC 构件设计来说,不存在类似于RC 构件中的最小配筋率概念.此外,在相同荷载条件下,配筋率越大的试验梁,挠度值越小.说明增加配筋可有效减小裂缝的开展,在相同的挠度值下,提高配筋率可缩小裂缝的分布区域.
4 极限抗弯承载力理论分析
为了进一步深入研究纵筋率对T 型截面UHPC梁的抗弯承载力的影响规律,本文基于截面内力分析,提出了T 型截面UHPC 梁的极限抗弯承载力计算公式,并结合本文中的试验结果与既有研究中的结果对所提出的公式进行验证.
4.1 基本假定
1)平截面假定,且钢筋与UHPC 之间不发生粘结滑移.
2)钢筋的应力应变关系参照《混凝土结构设计规范》(GB 50010—2015)[22],受拉钢筋的极限拉应变取0.01,如式(1)所示.
式中:εs为钢筋的应变;fy为钢筋的屈服强度;σs为钢筋的应力;Es为钢筋的弹性模量,取2 × 105MPa[22];εy为钢筋的屈服应变.
4.2 受弯承载力极限状态
试验发现:在持续加载过程中,受拉侧UHPC首先开裂,接着受拉侧纵筋发生屈服;中性轴不断向上并进入顶板,最终,截面受压侧最外缘UHPC 被压溃,T 型UHPC 梁达到正截面承载力极限状态.因此,UHPC 梁在达到极限抗弯承载力时的应变与应力沿梁高分布如图7 所示.图中:h为T 梁高度;k为UHPC 极限抗拉强度变化系数;ft为UHPC 极限抗拉强度;Ft为UHPC 受拉区合力;fc为UHPC 的轴心抗压强度;εcu为UHPC 的极限压应变;xe为等效受压区高度;Mu为极限抗弯承载力;xc1为受压区合力作用点到中性轴距离;Fc为受压区合力;As为纵向受拉钢筋的面积;xc为实际受压区高度;α为折减系数,本文中α为0.82;x为梁高;εs1为受压侧纵筋的压应变;As1为受压侧纵向钢筋的面积;εt受拉区边缘UHPC 拉应变.
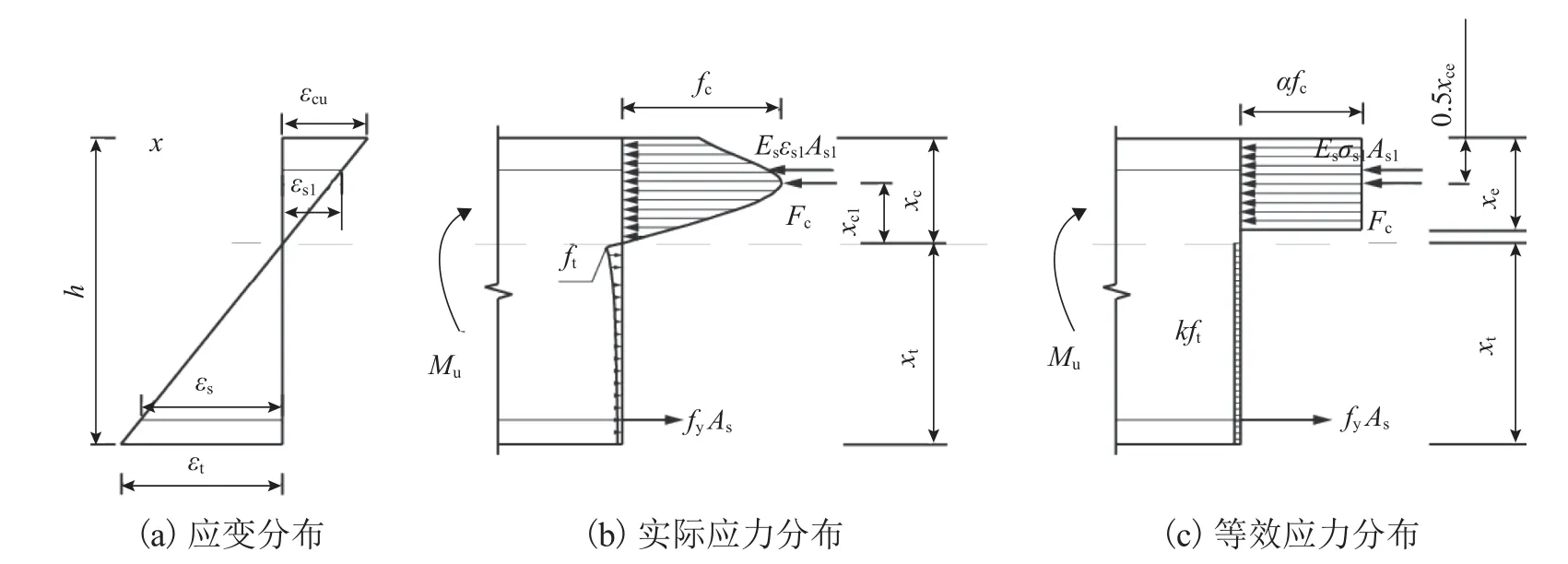
图7 受弯承载力极限状态Fig.7 Ultimate state of flexural capacity
4.3 UHPC 受压与受拉区的应力图形等效
为简化计算并增加承载力理论公式的实用性,UHPC 梁实际应力分布图形可以按照积分方法等效为矩形图形,并保持合力相等且合力作用点位置不变.UHPC 受压区合力为
式中:σc(εc)为受压区应力σc所对应的受压应变εc的函数;b(x)为梁截面沿梁高x的截面宽度函数,本研究中b(x)取定值顶板宽度bf.
UHPC 受压区合力作用点到中性轴距离xc1可由式(3)求得
对式(2)、(3)进行量纲处理,可得
式中:k1和k2为常数.
UHPC 等效受压区的α与β可由式(6)、(7)计算.
式中:β为等效受压区高度与实际受压区高度的比值,本文中β为0.83.
受拉区UHPC 的应力分布通过引入k,简化为矩形应力分布.因此,Ft可由式(8)表达.
式中:bw为腹板厚度,hw为腹板高度,hf为顶板高度.
4.4 T 型截面UHPC 梁的极限抗弯承载力公式
如图7(c)所示,根据截面内力平衡条件可得
如图7(a)所示,εs1可由式(10)表示.
式中:as1为受压纵筋形心到截面受压侧最外缘的距离.
将式(10)代入式(9),可得到一个关于xe的一元二次方程,通过求解xe,Mu可由式(11)计算得到.
式中:hf为顶板高度.
基于加载试验中极限抗弯承载力试验值(Mu_exp)结果反算k值.通过拟合k值与ρl的关系(图8(a)),可以看出:k与ρl近似线形关系,如式(12)所示.
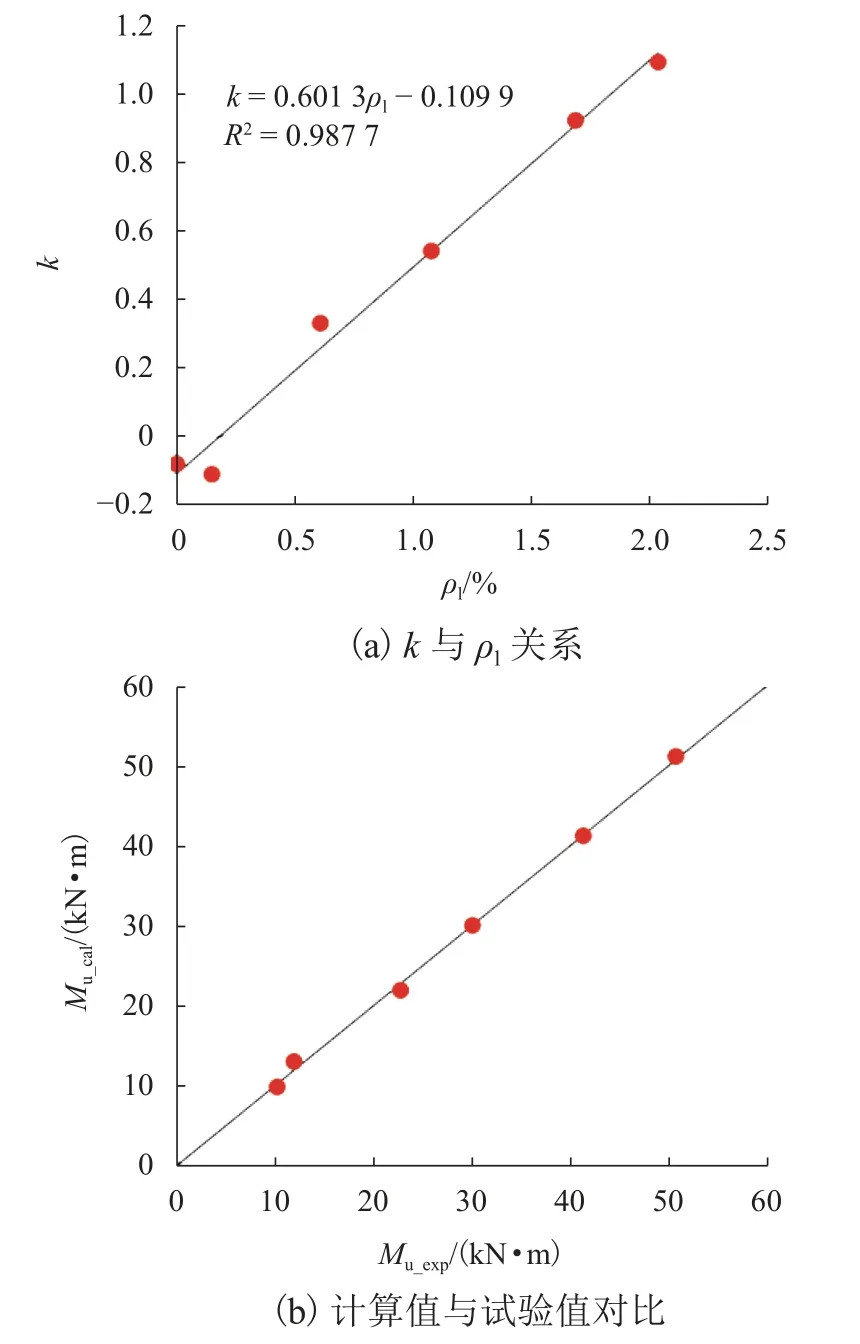
图8 极限抗弯承载力Fig.8 Ultimate flexural capacity
随着ρl的增加,k值也线性增加,说明纵筋率的增大可以显著发挥UHPC 的受拉性能.基于式(10)和式(11)可得T 型截面UHPC 梁的极限受弯承载力计算值(Mu_cal).6 根试件的计算值与试验值对比如图8(b)和表7 所示.其中,Mu_cal/Mu_exp的平均值为1.00,变异系数为4.63%,结果表明,所提出的计算式得到的计算值与试验值吻合良好.
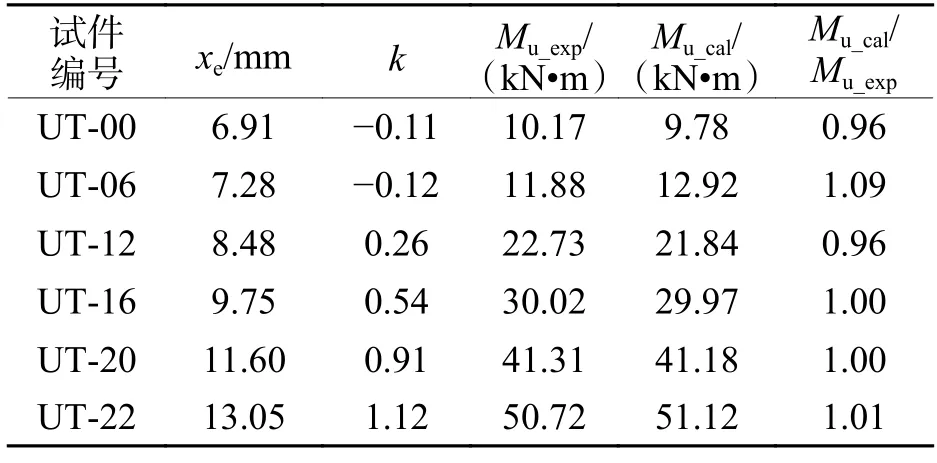
表7 T 梁受弯承载力计算值与试验值对比Tab.7 Comparison between calculated and experimental flexural capacity of T-shaped UHPC beams
4.5 公式适用性验证
为了对所提出公式进行进一步验证,基于检索到的相关文献[23-25]中出现的非预应力T 型截面UHPC梁的试验结果,对式(11)和式(12)的适用性进行了验证,如表8 所示.
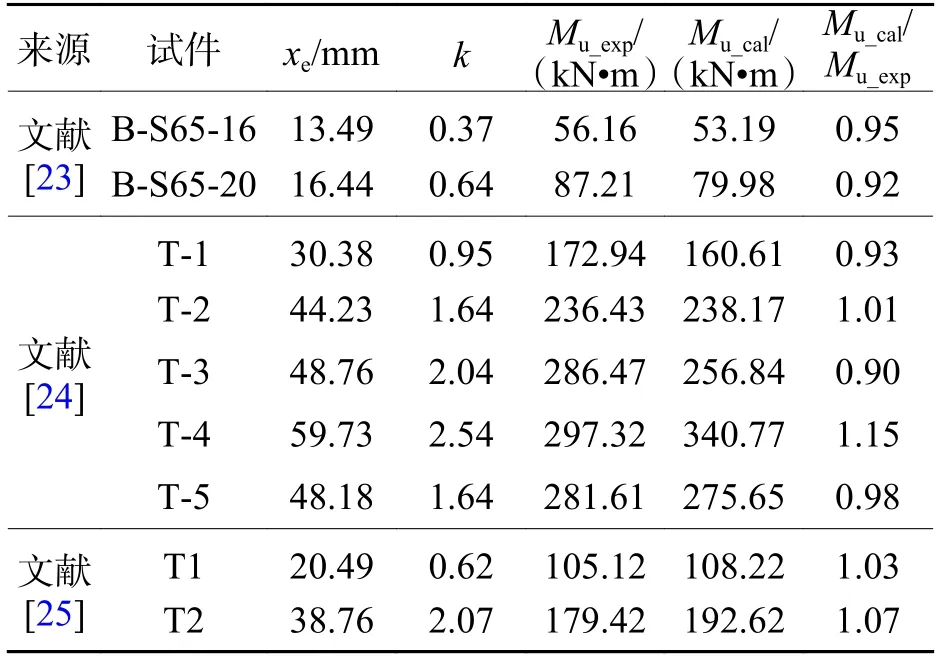
表8 既有文献的公式验证Tab.8 Validation of proposed equations in previous studies
图9 对比了既有文献以及本研究中的全部15 根T 型截面UHPC 梁的极限受弯承载力计算值与试验值.Mu_cal/Mu_exp的平均值为1.00,变异系数为6.80%,结果表明,所提出的计算公式适用性良好.
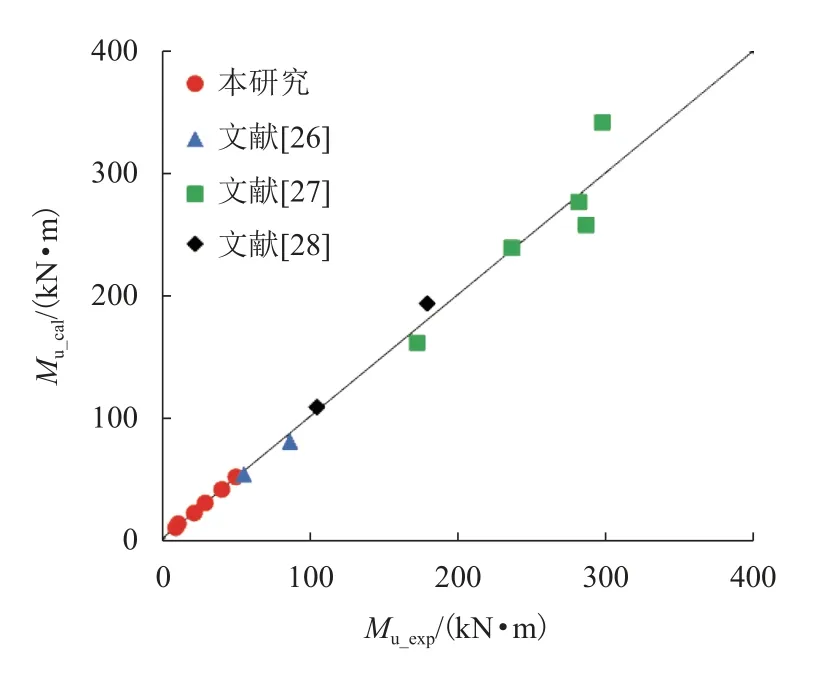
图9 提出公式的适用性分析Fig.9 Applicability analysis of proposed equations
5 结语
本文基于不同层次的试验与理论推导对UHPC华夫桥面单向T 梁中的纵筋率的影响进行了分析,提出考虑纵筋率变化的T 型截面UHPC 梁的极限受弯承载力计算式,并得到如下结论:
1)通过UHPC 单轴拉伸与压缩试验,得到UHPC在单轴拉伸荷载作用下,初裂强度为4.14 MPa,极限拉伸强度为8.42 MPa,极限拉伸应变为0.007 1,并表现出应变硬化现象;UHPC 在单轴压缩荷载作用下,轴心抗压强度为立方体抗压强度的85%.
2)6 根T 梁试件破坏全过程与RC 适筋梁类似,具备弹性、屈服与破坏阶段.无纵筋与纵筋率为0.15%的T 梁未发生类似RC 结构的少筋破坏,并具有屈服平台段,说明UHPC 构件中不存在RC 构件设计中最小配筋率概念.此外,随着纵筋率增加,T 梁抗弯承载力线性增加且裂缝分布越弥散.
3)基于截面分析法,通过基本假定和基于试验的本构模型,提出了T 型截面UHPC 梁的极限抗弯承载力计算式;基于试验反算结果,得到UHPC抗拉强度折减系数与纵筋率的关系;最终得到考虑纵筋率效应的T 型截面UHPC 梁的极限抗弯承载力计算公式;基于本研究和既有研究中的T 型截面UHPC 梁弯曲破坏试验结果,发现提出的T 型截面UHPC 梁的极限抗弯承载力计算式计算精度较高,与试验结果吻合良好并具有良好的适用性.
致谢:西南交通大学UHPC 真空管道梁桥基础研究(2682021ZTPY115).
