强震下大跨度连续梁桥损伤分析

2023-12-21贾宏宇吴炜昌彭奇慧郑史雄

西南交通大学学报 2023年6期

贾宏宇，吴炜昌，游刚，杨磊，彭奇慧，郑史雄

（1.西南交通大学土木工程学院，四川成都 610031；2.中铁二院工程集团有限责任公司，四川成都 610031；3.黄河勘测规划设计研究院有限公司，河南郑州 450003；4.西南交通大学机械工程学院，四川成都 610031）

我国地处欧亚板块、太平洋板块和印度板块之间，受3 大板块相互挤压，使西部、华北以及东南地区地震分布密集，地震频发[1].如2008 年四川汶川8.0 级地震，2010 年青海玉树7.1 级地震和2013 年四川雅安7.0 级地震[2]，造成众多桥梁开裂破坏，甚至倒塌.连续梁桥在地震区数量众多，其具备刚度大、行车平顺舒适和整体性好等特点.因此，研究大跨度连续梁桥在强震作用下的损伤破坏，对提高连续梁桥的抗倒塌能力有重要意义.

众多学者对桥梁损伤倒塌问题进行了研究：Hao 等[3]对一座双塔斜拉桥在爆炸荷载作用下的倒塌机理进行分析，探讨不同关键位置对桥梁连续倒塌的影响以及其损伤机理和灾变过程；谢文等[4]提出牺牲辅助墩来减小斜拉桥主塔的地震损伤，防止桥梁倒塌；仇清良等[5]采用LS-DYNA 对某6 跨连续梁桥进行倒塌仿真分析，对比研究了不同地震波输入下桥梁的破坏特征；黎雅乐等[6]通过连续梁桥地震振动台试验，分析连续梁桥非线性响应，研究连续梁桥的地震损伤演化和破坏过程；左烨等[7]对3 种混凝土梁桥进行非线性地震响应分析，模拟混凝土梁桥在强震作用下从损伤到倒塌的整个过程；王学伟[8]利用显式动力分析方法模拟水平纵向地震动作用下公铁两用斜拉桥整个倒塌过程和倒塌机理；黎雅乐等[9]通过能量比指标分析桥梁倒塌，提出一种基于结构层次的损伤评价指标来评估桥梁地震损伤情况；陈敬一等[10]为改进传统双层桥梁在地震损伤控制方面的不足，提出一种摇摆双层桥梁结构，对其地震反应和抗倒塌能力进行分析.还有一些学者对有限元在结构损伤倒塌分析中的可行性进行研究：周艳等[11]建立有限元模型，模拟了CyPress 高架桥的倒塌过程，与已有研究对比验证了倒塌分析模型的准确性，并对该桥梁破坏倒塌的原因进行讨论；徐俊祥等[12]利用LS-DYNA 模拟了近断层对土耳其Arifiye 大桥整个损伤破坏过程，与真实倒塌场景进行比较，验证了分析模型的合理性；Johnson 等[13]通过两跨连续混凝土桥梁的振动台试验和非线性数值分析对桥梁地震倒塌破坏进行研究，与相关试验结果进行对比，验证了数值模拟的有效性.以上国内外学者对桥梁非线性地震响应分析和损伤倒塌做了大量研究，但是大多只考虑部分构件非线性的影响，综合考虑材料非线性、大变形非线性和接触非线性的影响较少，有待进一步研究.

因此，本文基于一座大跨度连续梁桥，考虑桥墩材料非线性、损伤过程大变形非线性以及梁端非线性碰撞，在ANSYS/LS-DYNA 软件中建立全桥三维有限元模型，模拟其在纵横向强震作用下的损伤破坏过程，探究大跨连续梁桥在强震作用下的非线性动力响应规律和损伤破坏过程.

1 工程背景与有限元模拟

1.1 工程背景

本文以某大跨度连续梁桥为研究对象，梁体全长177.5 m.上部结构为单箱单室变截面箱梁，跨中梁高4 m，桥墩顶部梁高7 m，墩高32 m.箱梁顶板宽12.6 m，底板宽6.7 m.主桥有1 号、2 号2 个墩和0 号、3 号2 个桥台.其中，1 号墩设置纵向滑动支座，2 号墩上设置固定支座.桥梁具体信息如图1所示.

图1 桥梁尺寸示意（单位：cm）Fig.1 Bridge dimensions（unit: cm）

1.2 有限元模型

计算模型的总体坐标系以顺桥向为X轴，横桥向为Y轴，竖向为Z轴.钢筋采用梁单元BEAM161模拟，混凝土选取8 节点显式实体单元SOLID164模拟，为减少模型计算量，采用单点积分，为防止单元出现零能量变形模式，引入基于刚性的沙漏控制.桥墩有限元模型如图2 所示.假设钢筋混凝土之间完全粘结，忽略混凝土与钢筋间的粘结滑移，采用关键字*CONSTRAINED_BEAM_IN_SOLID_ID 约束钢筋与混凝土一起运动.该桥建在岩石地基上，故不考虑土-结构相互作用，墩底进行固结.

图2 桥墩有限元模型（单位：cm）Fig.2 Finite element model of bridge pier (unit: cm)

1.3 材料模型

桥梁动力分析中，为准确模拟损伤过程，在容易发生碰撞和破坏的桥墩和支座等区域进行网格细化，混凝土和钢筋分别采用弹塑性损伤帽盖模型（MAT_159）和等向强化弹塑性模型（MAT_003）模拟，如图3 所示[14].图中：I和I0分别为单轴拉伸试验的初始长度和变形长度；E和Et分别为弹性模量和切线模量；β为硬化参数，该值等于0 时为随动强化材料，该值等于1 时为各向同性强化材料，该参数取0～1 时则为混合强化材料.MAT_159 能较好地模拟桥墩混凝土的损伤行为，考虑地震作用下混凝土材料的应变率效应.根据Simo 等[15]提出的损伤理论，设置MAT_159 材料的单元失效限值ERODE.该模型的屈服面定义[16]为

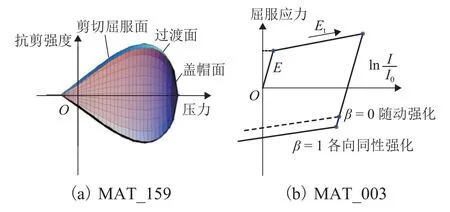
图3 材料模型Fig.3 Material models

式中：J1为第一应力不变量，J2和J3分别为第二和第三偏应力张量，Ff为剪切破坏面，Fc为帽盖面，κ为描述Fc的内变量，R 为角隅插值函数[14].

MAT_003 材料模型可通过塑性应变定义材料失效，利用Cowper-Symonds 模型考虑钢筋的应变率效应[17]，适用于梁、壳和实体单元，计算效率高.表1、2 列出了本文采用的材料特性.

表1 混凝土模型部分参数Tab.1 Partial parameters of concrete model

表2 钢筋模型部分参数Tab.2 Partial parameters of steel bar model

1.4 接触模型

采用罚函数法模拟大跨度连续梁桥有限元模型网格间的接触界面，在穿透节点和接触面之间的假想法向界面放置弹簧限制穿透[18].模型中支座上下表面与主梁底部和墩台顶部间采用自动面面接触.损伤过程中主梁与桥墩间接触采用关键字*CONTACT_ERODING_SURFACE_TO_SURFACE，破坏裸露的钢筋与混凝土之间接触采用关键字*CONTACT_AUTOMATIC_NODES_TO_SURFACE.刚性地面由关键字*RIGIDWAL 进行模拟，在刚性表面与变形体节点之间提供一种简单的接触算法[16].同时在*CONTROL_CONTACT 关键字中设置接触刚度比例因子SLSFAC 为0.1，避免计算过程出现两接触物穿透现象.

1.5 地震荷载模拟

该大跨度连续梁桥的场地属于Ⅱ类场地，抗震设防烈度为7 度，设计基本地震加速度值为0.15g，以设计反应谱为目标拟合地震加速度时程，最大幅值为5.0 m/s2，如图4 所示.图中，t为时间.采用中心差分法求解运动方程，时间步长为0.02 s.考虑一致地震激励，其中，纵向（X方向）与横向（Y方向）地震动强度比值为1∶0.85[19]，地震动激励选取X方向和X+Y方向2 种.在桥梁竖向同时考虑了重力加速度的作用，通过在LS-DYNA 中采用临界阻尼法对桥梁模型进行应力初始化来平衡重力荷载引起的动力响应.

图4 地震加速度时程Fig.4 Seismic acceleration time history

1.6 桥梁结构动力特性分析

基于ANSYS 软件中Modal 模块，采用Block Lanczos 法进行结构自振特性分析，计算该连续梁桥前10 阶自振频率及相应的振型，如表3 所示.分析可知，由于1 号墩设置纵向滑动支座，2 号墩设置固定支座，1 阶振型为主梁纵向振动，桥墩出现纵向弯曲，这和理论分析一致.

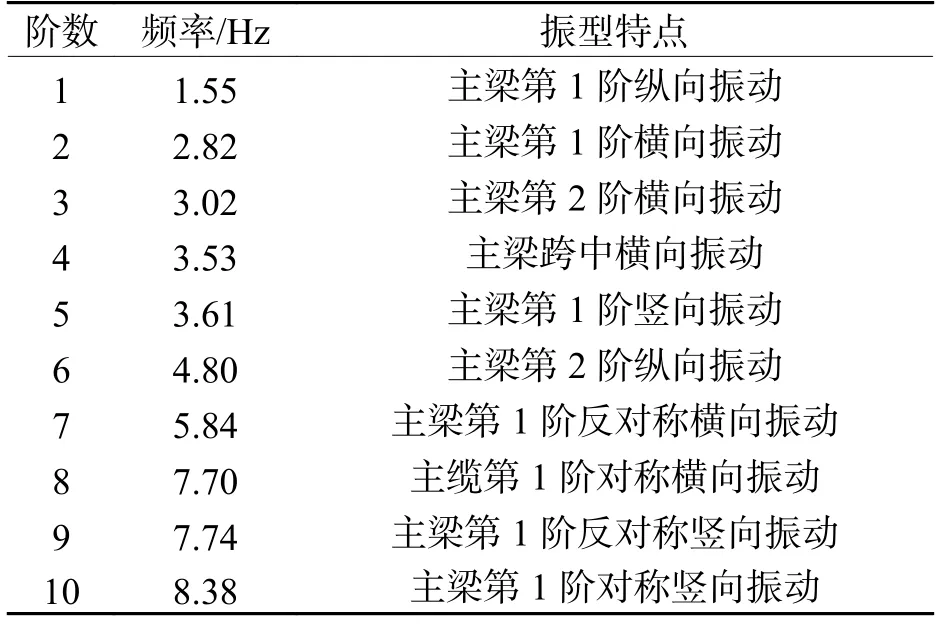
表3 桥梁动力特性Tab.3 Bridge dynamic characteristics

2 连续梁桥损伤破坏过程

大跨度连续梁桥的破坏是由于桥墩构件发生过大塑性变形，局部受力超过极限承载能力发生严重损伤引起.整个损伤破坏过程持续大约20 s，墩梁纵向相对位移和桥墩损伤如图5、6 所示.前2.5 s，在强震作用下连续梁桥的动力响应较小，桥墩混凝土尚未出现损伤，整体处于平稳状态；7.0 s 时右侧主梁与相邻桥台第1 次碰撞，桥梁动力响应出现小幅度增加，桥墩混凝土损伤不明显，全桥处于弹性阶段；12.0 s 左右发生第2 次碰撞，同时，左侧主梁也与相邻桥台发生第1 次碰撞，桥梁动力响应逐渐接近峰值，固定支座破坏，墩梁相对位移过大发生碰撞，右侧桥墩底部出现损伤破坏；随着地震持续进行，17.0 s 时右墩应力减小，而左墩应力增大，右边桥墩底部发生受弯塑性破坏，最后桥梁损伤破坏.

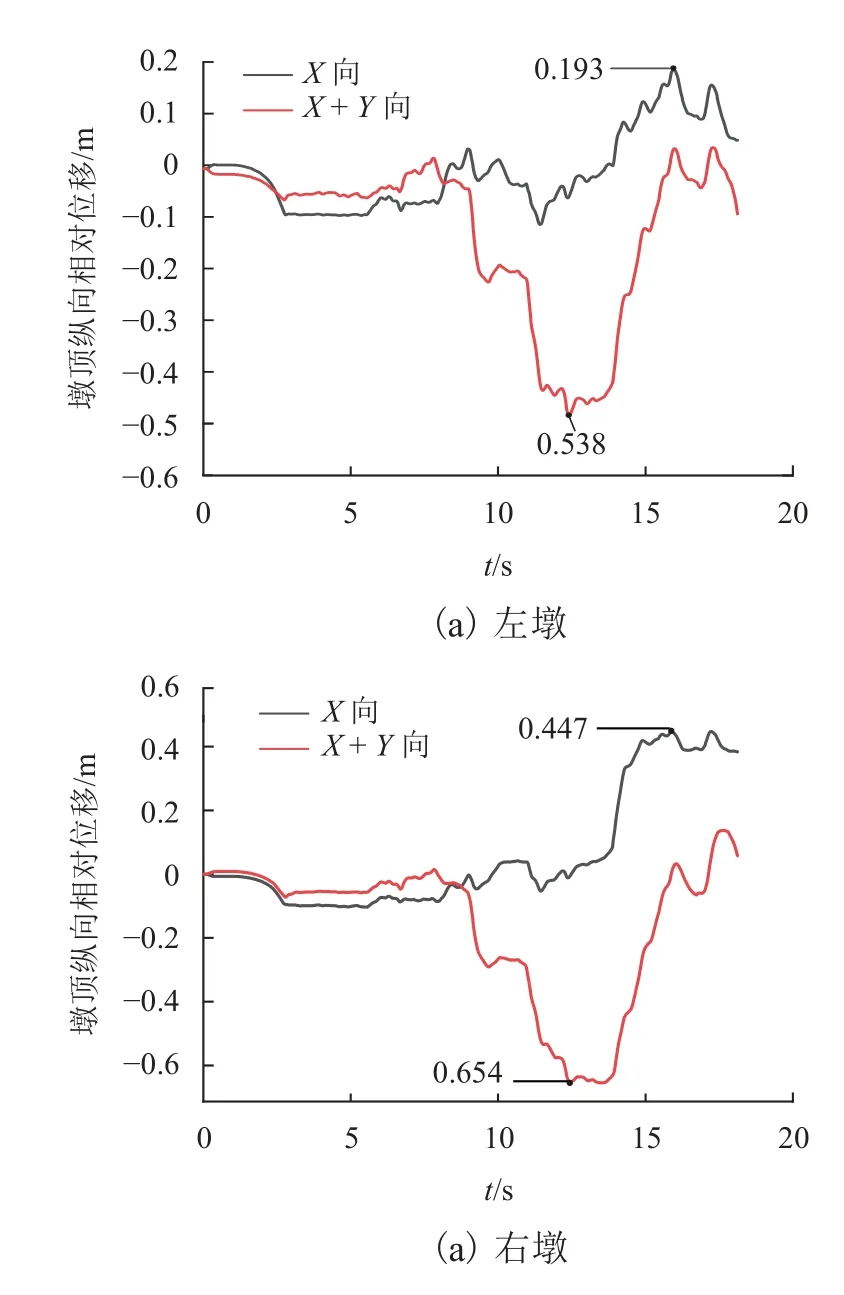
图5 墩顶与主梁纵向相对位移Fig.5 Longitudinal relative displacement of pier top and main beam

图6 0～17.0 s 损伤破坏过程Fig.6 Damage process of 0～17.0 s

3 连续梁桥损伤破坏机理分析

3.1 主梁应变响应

为探究不同工况对连续梁桥非线性地震响应的影响，选取主梁为研究对象，数据结果如图7所示.

图7 主梁应变响应Fig.7 Strain response of main beam

从左到右连续梁桥3 跨主梁的应变峰值依次增大，跨中和右边跨应变相近，说明中跨跨度大竖向刚度小和固定支座约束，使得跨中和右边跨在地震作用下有更大响应；同时，各地震激励方向下右边跨跨中应变峰值约是左边跨跨中应变峰值的2 倍，因为地震作用下桥梁固定墩侧底部出现损伤破坏，桥墩发生竖向位移，在自重作用下向下移动，导致右边跨跨中出现更大的应变.对各主梁而言，双向地震动作用下主梁应变是单向地震动作用下主梁应变的1.3 倍，但不同工况作用下各主梁应变变化趋势基本一致，说明虽然双向地震动作用较单向地震动对主梁应变响应影响更大，但桥梁应变响应总体变化规律由桥梁结构自身决定.

3.2 位移响应

考虑到地震作用下桥梁损伤破坏过程中会出现较大位移响应，引起构件局部损伤，甚至破坏.基于这种考虑，选取主梁梁端和墩顶位移响应进行分析，结果如图8 所示.

图8 主梁和桥墩位移响应Fig.8 Displacement responses of main beam and bridge pier

由图8（a）、（b）可知，无论是单向地震动作用还是双向地震动作用，主梁梁端纵向位移变化规律基本一致，说明主梁位移响应和损伤规律由桥梁结构自身决定，地震动多维性对其影响较小.7.0 s 前，墩顶相对位移波动较小，7.0 s 后墩顶相对位移变化剧烈，当12.5 s 时最大纵向相对位移达到0.723 m，横向位移达到0.316 m，此后相对位移逐渐减小，如图8（c）～（f）所示.双向地震动作用下，桥墩最大纵向和横向相对位移都大于单向地震动作用下的相对位移，且峰值位移出现时间也提前3.0 s 左右.双向地震动对桥墩位移响应影响较大，但未改变其破坏模式.

3.3 桥墩损伤分析

由图8（c）、（d）可知，在双向地震动作用下1 号桥墩和2 号桥墩的最大纵向相对位移都超过0.500 m，但2 号桥墩位移比1 号桥墩位移大35.6%，墩底混凝土出现压溃时，2 号桥墩损伤破坏更加严重.故本文选取2 号桥墩为研究对象，通过单元平均损伤因子[20]对桥墩进行损伤分析.桥墩损伤因子随着桥墩混凝土的损伤发展从0～1.00 变化，当桥墩混凝土损伤因子为0 时，桥墩尚未发生损伤；当桥墩混凝土损伤为1.00 时，桥墩已经完全损伤破坏.

桥墩的地震损伤是一个逐渐发展的过程，而双向地震动会推进和加剧桥墩损伤，使桥墩更早进入塑性破坏，其中，墩底是损伤破坏最为严重的部位，如图9 和图10 所示.由图9、10 可知：前7.0 s 桥墩损伤并不明显，随着时间的增加，第9.0 s 墩底混凝土开始出现损伤，到17.0 s 时墩底大部分混凝土达到失效状态，即平均损伤因子达到0.99，此时桥墩已经出现严重破坏即将倒塌，之后损伤因子下降明显，墩底出现大面积混凝土失效.对整个大跨度连续梁桥而言，桥墩损伤首先在墩底出现损伤，累积到一定程度时桥墩底部发生过大塑性变形，出现开裂破坏，进入到塑性破坏阶段直至垮塌.

图9 桥墩破坏区域平均损伤因子Fig.9 Average damage factor of bridge pier damage area

图10 桥墩部分损伤云图Fig.10 Partial damage cloud maps of bridge pier

4 连续梁桥碰撞效应分析

实际地震中连续梁桥的主梁与桥台常发生纵向碰撞，考虑桥台约束作用，接触间隙为0.1 m，梁-台碰撞力如图11.2.5 s 左右2 种工况发生第1 次碰撞，主梁应变在0.000 1～0.000 9，纵向位移约0.1 m，如图7 和图8（a）、（b）；9.0 s 左右，左边梁端碰撞力达到峰值87 kN，但持续时间较短，左边跨主梁的应变和位移响应也接近各自峰值，右边跨主梁应变则小幅度增加到0.000 2；14.0 s 时右边梁端碰撞力达到峰值98 kN，为初始碰撞力30 kN 的3.3 倍，相比左边梁端碰撞更激烈且持续时间较长，同时，右边跨主梁的应变和位移响应出现激增，接近峰值.以上响应和理论分析一致，由于1 号墩设置纵向滑动支座，2 号墩设置固定支座，使得主梁纵向振动时，右边梁端碰撞更早且频繁.此外，由碰撞引起的梁截面损伤主要集中在箱梁翼缘和底部，双向地震动碰撞损伤较明显，如图12.图中：蓝色代表混凝土处于弹性阶段，绿黄色表明混凝土逐渐进入塑性阶段发展，红色说明混凝土损伤严重.

图12 梁端碰撞应力云图Fig.12 Beam end collision stress cloud map

可见，碰撞使得桥梁结构在地震作用下的动力响应更加复杂多变.因此，在实际工程应用中桥梁的碰撞问题应予以考虑，加强关键部位的防护和强化，防止强震作用使梁端损伤严重而破坏.

5 连续梁桥损伤破坏机制分析

全桥损伤破坏过程经历以下4 个阶段：

1）阶段 1（t=0～2.5 s）

碰撞前，主梁应变和墩顶相对位移基本为0，未出现较大波动变化，如图7 和图8（c）～（f）所示.各桥墩的应力相对较小，左墩底应力约0.5 MPa，右墩底应力约3.0 MPa，如图13 所示.桥梁处于平稳状态.

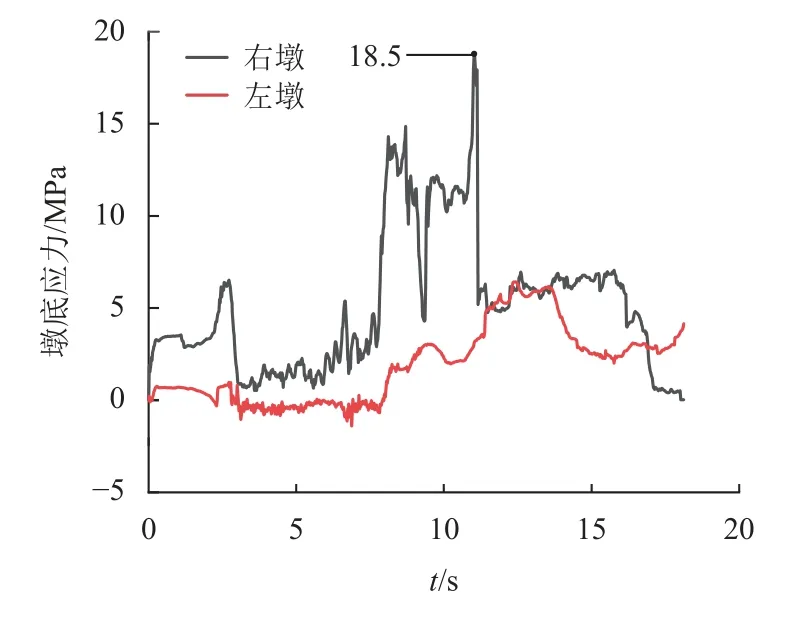
图13 桥墩底应力Fig.13 Bridge pier bottom stress

2）阶段 2（t=2.5～7.0 s）

t=2.5 s 时右边梁端发生第1 次碰撞，右边梁端碰撞力约30 kN，主梁应变和墩梁位移出现第1 次小增幅，主梁应变最大为0.000 9，纵向相对位移为0.100 m，见图7 和图8；桥墩混凝土损伤因子为0，尚未出现明显损伤.全桥处于弹性阶段.

3）阶段 3（t=7.0～12.5 s）

t=7.0 s 时，右边梁端发生第2 次碰撞，使得主梁内力进一步增加，碰撞力达到60 kN.由图8（c）～（f）可知，t=9.0 s 时，固定支座处墩梁纵向和横向相对位移增加2 倍，且随时间推移继续增加，位移过大固定支座失效.右边桥墩底部混凝土损伤因子约0.25，出现混凝土失效破坏.

4）阶段 4（t=12.5～20.0 s）

t=12.5 s 时，墩底应力达到峰值18.5 MPa，墩梁纵向相对位移达到最大值0.723 m，右边桥墩发生过大塑性变形出现受弯破坏，导致此阶段右墩应力减小，而左墩的应力增大，如图13 所示.当t=17.0 s时，墩底破坏处混凝土平均损伤因子达到0.99，随后损伤因子开始变小，混凝土单元出现大面积失效，墩底应力不断减小.这是因为此时右墩墩底混凝土出现严重破坏，右墩丧失支撑作用，桥梁发生损伤破坏.

由此可得，强震作用下大跨度连续梁桥主要损伤破坏过程：地震作用前7.0 s，桥梁动力响应和损伤较小，随着地震持续进行，桥墩混凝土损伤不断累积，固定墩的墩底应力达到最大值18.5 MPa，约1/3桥墩面积发生损伤，直至混凝土损伤因子达到0.99，全桥丧失支撑作用，发生严重损伤破坏.