基于大涡模拟的波状前缘水翼空化抑制研究

2023-12-21马楷东曹留帅万德成

海洋工程 2023年6期

马楷东，曹留帅，万德成

（上海交通大学船海计算水动力学研究中心船舶海洋与建筑工程学院，上海 200240）

空化是一种复杂的相变现象，一直是水动力学领域的经典和基础性问题。当液体介质中的局部压力低于环境温度下的饱和蒸汽压时，液体介质中就会出现空泡。这种空泡的形成、发展和溃灭过程以及由此产生的一系列物理变化称为空化。空化具有明显的空间流动性和剧烈的非定常性，往往会造成严重的水动力性能损失，并造成侵蚀、噪声、振动等不利影响［1］。Wang 等［2］利用Clark-Y 翼型进行了空化试验，通过改变空化数和水翼攻角，对不同条件下空化流动的结构进行了识别与分析，总结了水翼周围空化流的定常和非定常特性。Ji 等［3］采用均匀空化模型和大涡模拟相结合的方法，对NACA66 水翼周围的非定常空化流进行了数值模拟，对空化周期性演化、空化—涡流相互作用和空化引起的压力脉动等复杂流动行为进行了机理研究和总结。

由于空化现象的产生大多伴随负面效应，因此对空化的抑制便成为了新的研究热点。根据当前研究成果，可以将空化控制手段分为两类：主动控制方法和被动控制方法。主动控制方法是指从系统外部向内部注入能量控制流动结构，进而控制空化，例如注入聚合物、水、空气或利用超声波等。Lu等［4］在NACA66水翼吸力面进行开孔射流，实现了对水翼片状及云空化的高效抑制。王子豪［5］以NACA0015 水翼模型作为研究对象对局部自然空化流动的演变机理进行深入研究，通过空泡形态、压力脉动、速度场等特性，重点分析冲击波机制下空化流场的演化规律。主动控制方法虽然在空化抑制方面取得了一定的效果，但需要诸如射流、通气等外部条件进行干预，在工程应用中实现难度大且成本较高。因此，作用力来自于系统本身且不借助于外部能量的被动控制方法被广泛研究。车邦祥［6］通过微涡发生器方法对水翼空化进行了试验和模拟两方面的研究，对附着型空化的被动控制进行了详实的研究，文章还总结了常见的被动控制方法，如加装横向障碍物、挖设沟槽或改变表面粗糙度等。其中，有一种运用仿生学原理，对水翼进行表面构型改变，以控制近壁面流体流动特性进而控制空化的方法引起了学者们的关注。研究发现，海洋生物座头鲸的鳍肢前部有波状的凸结，这种凸结结构可以帮助座头鲸鳍肢在很大攻角下摆动，而不会产生失速现象，并且可以有效地控制流动分离，减小游动阻力。于是，开始有学者将这种波状凸结构型应用到了控制空化的研究中。Custodio等［7］以NACA634-021翼型为基准，试验测量了不同波长和波幅组合的波状水翼在不同攻角下的初生空化数、升阻力系数和升阻比等数据，结果发现，波幅较大的波状水翼空化区域范围明显减小，而波长似乎对空化现象的影响很小。陈柳等［8］采用SSTk-ω湍流模型对多种波状水翼进行了数值模拟分析，发现凸结构型导致了一系列规律的对转涡带，限制了空泡的展向发展，对空化具有抑制效果。但由于雷诺时均方法（Reynolds-averaged Navier-Stokes，简称RANS）无法显示空化流场的细节信息，大涡模拟方法（large eddy simulation，简称LES）开始得到应用。Pendar 等［9］对波状水翼非定常空化特性进行了大涡模拟研究，发现凸结的存在使来流汇聚到波谷处，从而加速波谷处的流体流动，使其压力变低，空化易于从此处产生。文章重点研究了不同构型波状水翼表面的流动分离现象对空化的影响，但并没有计算诸如空泡体积等数据。Li等［10］基于LES方法对大攻角下的波状水翼进行了数值模拟研究，结果表明减小波长和增加振幅不仅可以使空化体积减小约30%，还可以控制空化脱落的不稳定性，降低压力幅值。但该规律特性对小攻角工况下的波状水翼是否适用仍有待考量。因此，Zhao 等［11］运用等升力原理提出了不同的观点，在详细比较了小攻角波状水翼空化的周期特性、压力脉动以及空化对流向涡的影响等关键流动特性后发现，在该工况下波浪型前缘的空泡体积并没有明显减小，但是有效抑制了压力脉动，文章分析可能是等升力原理导致了不同结论的产生。

通过以上分析发现，目前关于波状水翼空化抑制的试验和数值模拟研究还不够充分，对其内在机理和影响规律的认识还不全面，因此，采用大涡模拟方法对三维波状水翼的空化现象进行精细化仿真，通过空化周期、升阻力系数、压力脉动以及流向涡结构等流场特性分析，探究前缘波浪曲线的波幅和波长对水翼空化的影响规律和内在机理，为波状水翼的空化抑制研究提供参考和经验。

1 数学模型

1.1 控制方程和LES方法

在模拟所采用的混合介质模型中，假设蒸汽和液体的速度和压力相同，基本控制方程由连续性方程和动量守恒方程组成，表示形式如下：

式中：ui为i方向上的速度分量，p是混合物压力。假设蒸汽和液体的压力值相同，μ是层流黏度，ρ是混合介质密度。μ和ρ的表达式为：

大涡模拟方法通过滤波函数将大尺度的涡和小尺度的涡分离开，大尺度涡直接模拟，小尺度涡用亚格子模型来封闭，提供细节化的流场信息。将式（1）和式（2）进行滤波运算后，得到的LES方程为：

式中：下标l和v分别代表液相和气相，αv是蒸汽体积分数。τij被称为亚格子（SGS）应力，其定义如下：

为了构造亚格子应力的封闭模型，需要对未知的亚格子应力进行建模处理。假设亚格子应力与可求解尺度的应变张量系数-Sij成比例，将小涡对大涡的影响关联起来：

式中：τkk为亚格子应力中各向同性部分；μt为亚格子模型的湍流黏度；δij为克罗内克符号，i=j时，δij=1，i≠j时，δij=0。采用的亚格子模型为Nicoud 和Ducros［12］提出的WALE（wall-adapting local eddy-viscosity）亚格子模型，该模型在求解空化问题上具有很好的适用性。其湍流黏度μt表达式为：

其中，Ls是亚格子尺度的混合长度，其定义如下：

其中，k为von Karman 常数，d为到最近壁面的距离，V为计算单元的体积，Cw为默认的WALE 常数，取值为0.5。

1.2 空化模型

采用Schnerr 和Sauer 基于Rayleigh-Plesset 方程所提出的Schnerr-Sauer 空化模型来描述气、液传质过程［13］。该模型的优点是源项表达式不包含经验常数，具有较高的普适性。空化模型的方程为：

其中，代表蒸发率ṁ+和冷凝率ṁ-的质量源项定义为：

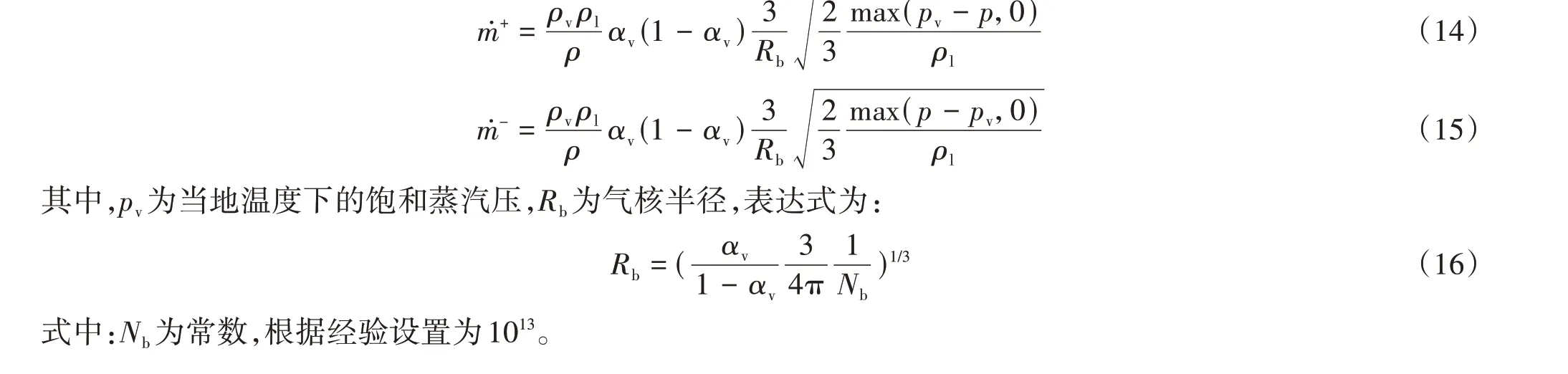
2 数值模拟

2.1 几何模型

将座头鲸鳍肢前缘凸结引入到水翼设计中，采用波浪状构型做仿生处理。由于座头鲸鳍肢前缘比较肥大，因此选取NACA634-021翼型截面进行三维翼型建模，水翼弦长c=102 mm，厚翼特点明显。模型截面的横坐标以最大厚度0.35c处为分界点，前缘重构，尾缘不变，如图1所示。波状水翼前缘曲线由余弦曲线构造：

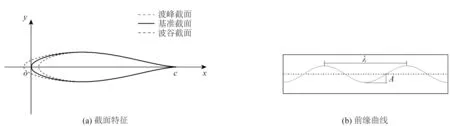
图1 模型参数示意Fig.1 Model parameters and definition

式中：z为水翼的展向坐标，A为波幅，λ为波长。

为了研究基准水翼与波状水翼空化的区别，并探究不同前缘波幅和波长对波状水翼的影响和规律，进行了参数化建模，各水翼几何模型如图2所示，模型参数及命名见表1。

表1 前缘波幅与波长参数Tab.1 Leading edge amplitude and wavelength parameters

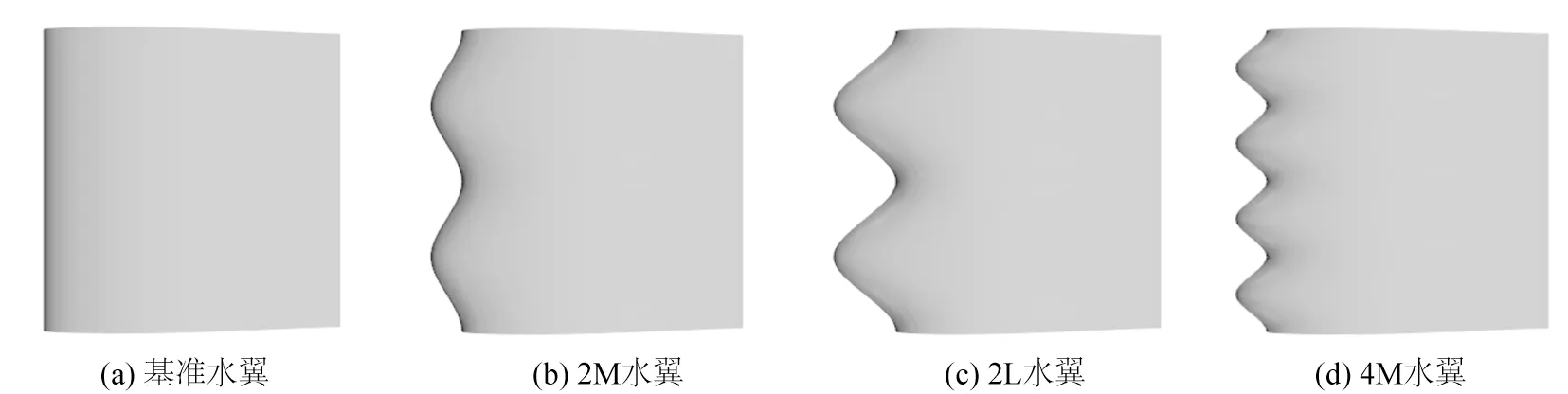
图2 水翼几何模型Fig.2 Geometric model of hydrofoils

2.2 计算域和边界条件

计算域和边界条件设置如图3所示，水翼攻角αAoA= 6°，计算域入口位于翼前缘4倍弦长处，出口位于翼尾缘7倍弦长处，可以保证稳定的来流，并使尾流充分发展。

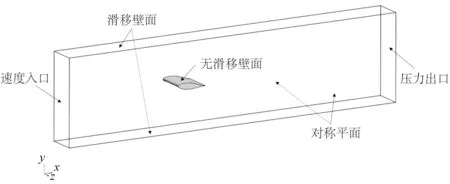
图3 计算域和边界条件Fig.3 Computational domain and boundary conditions

为了防止壁面的影响，两侧边界做对称平面处理；上下边界设置为自由滑移壁面；入口和出口边界分别设置为速度入口和压力出口，出口压力值p∞根据空化数计算公式得出：

式中：σ为空化数，pv为试验环境下的饱和蒸汽压（模拟选取的环境温度为20 ℃），ρl为液体介质的密度，U为来流速度。具体的模拟工况在表2中给出。

表2 模拟工况参数Tab.2 Simulated operating parameters

在进行非定常空化数值求解计算时，时间步长的选取尤为关键。一般通过库朗数确定时间步长，这种方法结合时间参数与空间参数，通常选取库朗数为1或小于1的值进行计算：

式中：Δt为时间步长，Δx为网格特征尺寸。模拟的时间步长设置为5×10-5s。

2.3 网格验证与对比

2.3.1 网格无关性验证

网格采用结构化网格划分形式。为了确保模拟的准确性和精确度，设置了3 套网格进行网格无关性验证。3套网格按网格量分为粗网格、中等网格、细网格，对无空化下的升阻力系数进行了对比，公式为：

式中：FL和FD分别为升力和阻力，S为水翼的正投影面积。网格无关性对比结果在表3中给出。由于大涡模拟对网格质量要求严格，3 套网格通过调整第一层网格高度保证水翼表面处的无量纲距离y+值均小于1，如图4所示。

表3 网格无关性验证Tab.3 Grid independence verification

图4 网格y+值分布Fig.4 Distributions of y+ under different grids

在表3中，中等网格和细网格的模拟结果比较接近。在保证模拟精度和平衡计算量的前提下，选取中等网格进行后续的数值模拟计算分析。图5给出了基准水翼和不同的波状水翼表面网格和侧面边界网格划分情况。

图5 不同水翼网格划分Fig.5 The meshes around different hydrofoils

2.3.2 试验结果对比

为了验证所建立数值模型的适用性和正确性，选取基准水翼和2M 水翼进行升阻力系数的试验验证。参考Johari［14］得出的雷诺数Re=4.5×105的试验数据，对比结果在表4 中给出。结果表明一致性较好，说明所建立的数值模型具有良好的适用性。

表4 计算与试验对比Tab.4 Simulation and experimental comparison

3 结果分析

3.1 空化周期

为了对比研究基准水翼和波状水翼空化现象的区别，对不同水翼的典型空化周期进行可视化处理，如图6所示，将空化蒸汽体积分数为0.49的等值面和水翼表面压力系数Cp叠加显示，以便直观地揭示波状水翼前缘凸结对空化产生和发展的直接影响。

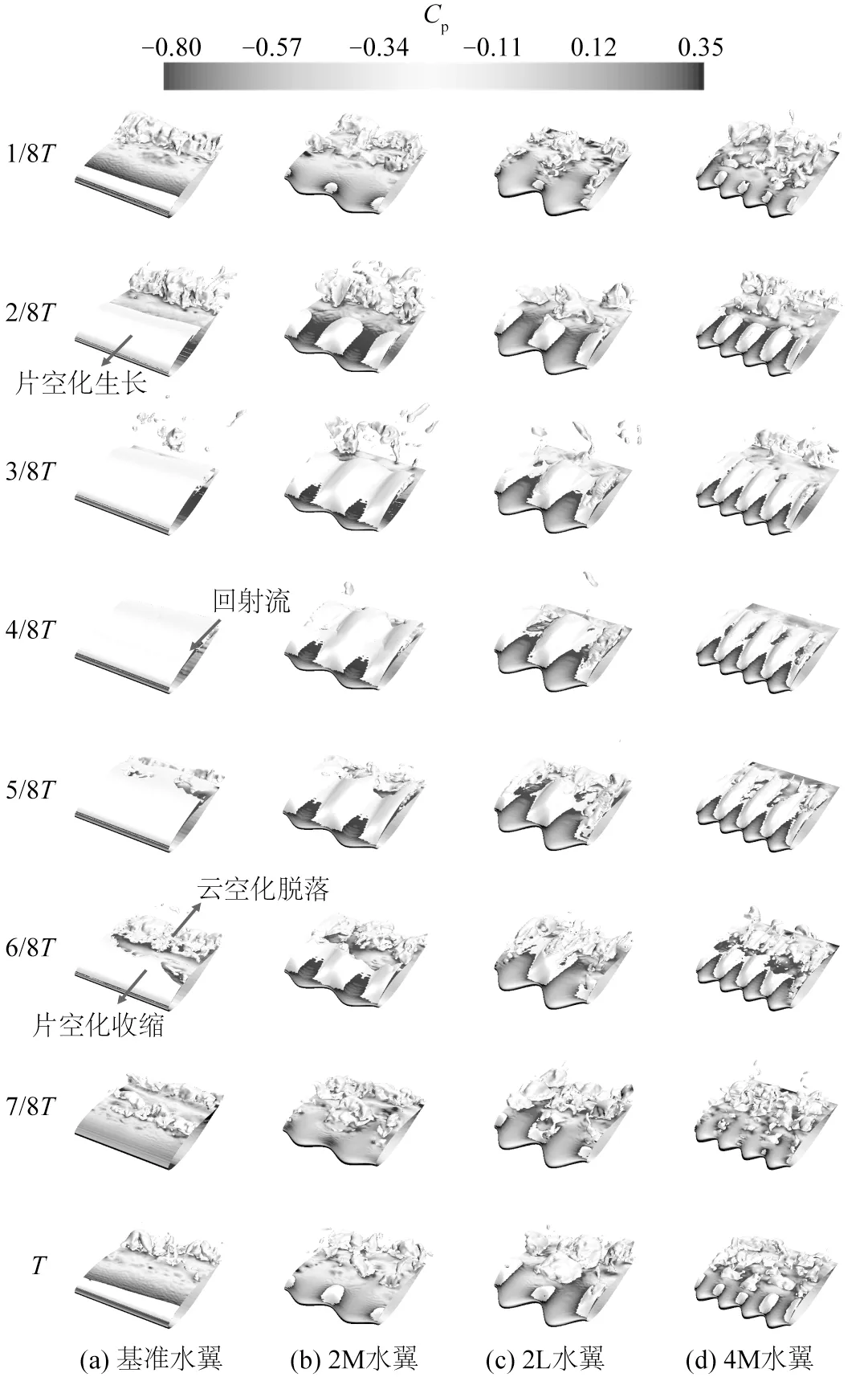
图6 典型空化周期（等值面αv=0.49）Fig.6 Typical cavitation cycle (The iso-surface of αv=0.49)

对于基准水翼，在图6（a）的1/8T～4/8T过程中，空泡从前缘初生，附着在水翼表面并在整个展向上连续分布，不断向后发展，当逆压力梯度足以克服水翼表面附近的湍流强度时，造成空泡断裂的回射流产生。如图6（a）的5/8T所示，空化由片状空化发展成云状空化，并出现空泡破裂和脱落现象。前端断裂的片空泡不断向前收缩，直至全部消失，图6（a）的6/8T～7/8T可以清晰地反映这一现象。而如图6（a）的T所示，尾端脱落的云空泡随流场向后运动，当局部压力恢复到饱和蒸汽压以上时，云空泡消失，并在水翼前缘开始新一轮的空化现象。观察空化周期云图发现，波状水翼的空化过程和基准水翼具有相似性，但由于前缘波浪构型使得空泡只在波谷处产生，如图6（b）、（c）、（d）所示，初生的片空泡在整个展向上是不连续的。对2M 水翼进行分析，发现波峰处的压力相对较高不利于空泡的产生，空泡起始于波谷处的低压区并向后延伸，而波峰似乎起到了分隔作用，限制了空泡的展向发展。当波谷处产生的片空泡延伸到一定长度后，受到来自前缘波峰的影响越来越小，空泡在展向上开始融合，并发展成与基准水翼相同的脱落模式，往复循环，周而复始。结合相关文献，将这种波峰波谷对空化发展的影响定义为分区效应。其内在机理是通过前缘波浪构型将来流进行整合，使流经波谷处的流速加快，压力降低，利于空化的产生，而波峰处由于流体介质在波谷处的聚集，相对压力较高，则没有空化的产生。

为了更好地探究前缘参数对空化的控制效果和作用规律，通过改变波状水翼前缘构型的波幅和波长进行对比分析。如图6（c）的2L 水翼所示，增大了前缘波幅，其整体的空化流动模式与2M 水翼相同，但仔细对比后发现，经过发展后的片空泡并没有在展向进行很好地融合，其每个波谷产生的空泡在展向上几乎相互独立，在回射流的作用下片空泡断裂，脱落形成的云空泡也是各自独立的，只在远场会产生干扰，波幅较大的波状水翼其空化分区效应更加显著。观察图6（c）的T发现，新一轮的空化周期开始时，两侧波谷的空泡要比中间的空泡发展更快，说明各个波谷产生的空化自成体系，循环周期不同步。对于波长的影响，在图6（d）所示的4M 水翼空化过程中，不同波长下的波状水翼空化发展模式相同，但是在展向空泡融合上，小波长水翼要弱于大波长水翼，波谷处产生的空泡虽然独立性明显，却有着同步的循环周期。因此，波幅和波长的改变都会对空化流场产生影响，增大波幅和减小波长都增强波状水翼的分区效应，控制空泡的产生和发展。

为了进一步研究前缘波浪构型对空化控制的影响，图7对水翼的空泡体积进行了时均处理。对比发现，波状水翼的时均空泡体积都低于基准水翼，说明波浪型前缘的引入可以对空化进行抑制。进行定量分析后发现，2M 水翼的空化抑制率为15.7%，2L 水翼的空化抑制率比2M 水翼稍高为18.6%，说明波幅较大的波状水翼对空化的控制效果更明显。而4M 水翼的空化抑制率为27.9%，相比于2M 水翼对空化的控制水平大大提高，说明减小波长可以大幅提高波状水翼对空化的抑制效果。这种大波幅和小波长控制效果良好的结果应该与分区效应导致空泡间相互独立，限制了展向抬升有关。

图7 时均空泡体积Fig.7 Time-averaged vapor volumes

3.2 升阻力性能

图8显示了不同水翼的时均升力系数和阻力系数。在空化过程中，由于波状水翼的空化受到抑制效果，其升力系数相比于基准水翼都得到了不同程度的提升。对比2M和2L水翼，升力系数随波幅的增大而减小，与波幅大小成反比，阻力系数则与波幅大小成正比关系，升阻比随波幅的增大而减小；对比2M 水翼和4M 水翼，升力系数与波长大小成正比关系，前缘波长越大，升力系数越大，阻力系数与波长成反比关系，升阻比随波长的减小而增大。结果表明，波浪型前缘可以一定程度上提高水翼的升力系数，但阻力系数也会随之变大，无法保证升阻比的变化规律，故合适的幅长比有利于提高水翼的水动力性能，超过一定限值后性能则会下降。

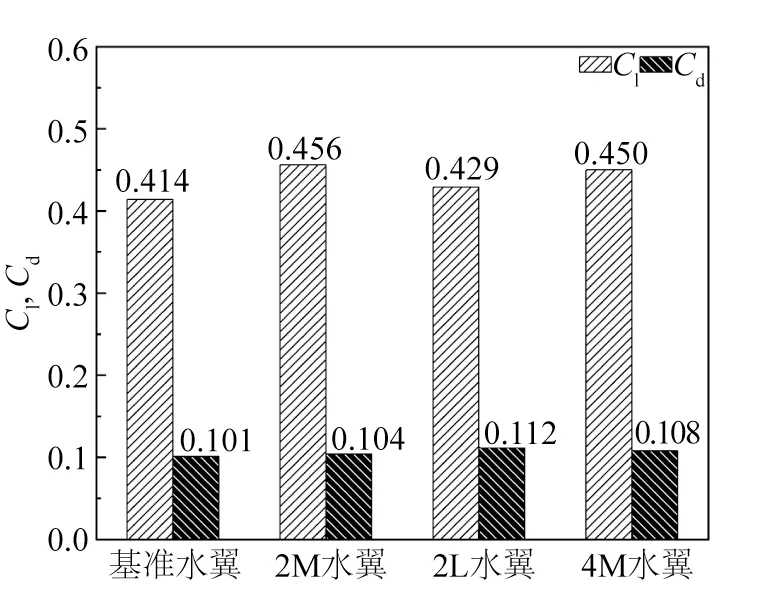
图8 时均升阻力系数Fig.8 Time-averaged lift coefficients and drag coefficients

下面进一步对升力系数进行时域统计。从图6中可以看出水翼空化是具有周期性的，故将物理时间t无量纲化，处理后的特征周期参数T定义如下［11］：

如图9 所示，截取了4 种水翼空化过程中一个典型周期内的升力系数和空泡体积分布。可以清晰地发现基准水翼升力系数的数值振荡比较剧烈，非定常特性明显，存在较大的升力波动。升力的产生源于水翼上下表面的压力差，故也可从侧面分析出基准水翼的压力脉动是比较明显的。而波状水翼升力系数的振荡处于较低水平，没有明显的峰值，表明在空化状态下，波状水翼获得的升力相对稳定，受到空泡发展和溃灭的影响较小，水动力性能优越。

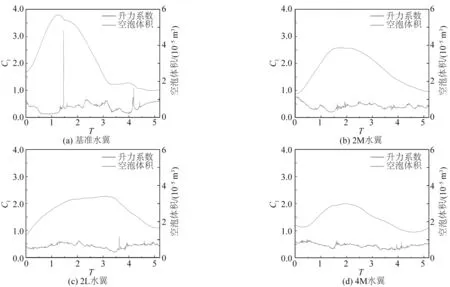
图9 一个典型周期内空泡体积和升力系数的时域曲线Fig.9 Time-domain curve of the vapor volume and lift coefficient in one typical cycle

3.3 压力脉动

将表面压力系数做时均化处理，可以更好地分析波状水翼对空化控制的内在机理，帮助理解空化的非定常特性及规律。如图10所示，深色附近为低压区，即空化初生的区域。在基准水翼表面低压区连续均匀，所以空泡也是在整个水翼展向均匀分布的。而波状水翼的低压区只在波谷处存在且不连续，波峰处显示为高压区，故空化不从此处产生。

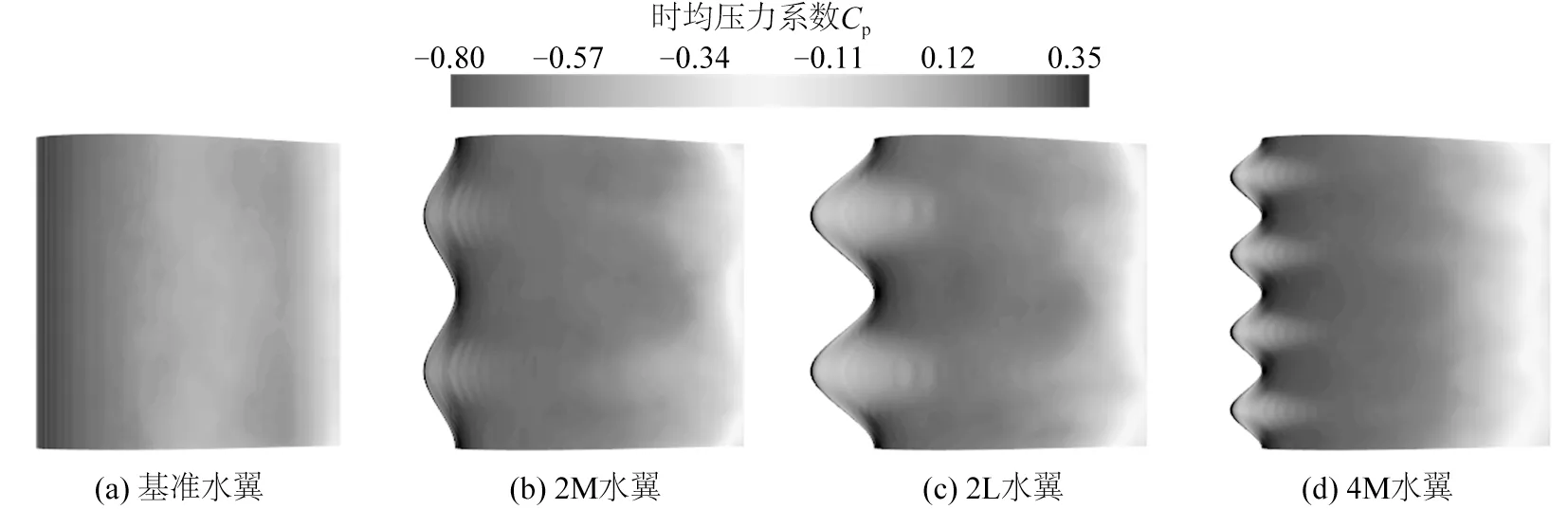
图10 吸力侧时均压力分布Fig.10 Distribution of time-averaged pressure on suction side

对比图10（b）和图10（c），不同波幅下波状水翼波谷处低压区在展向和流向并没有太大区别，但是由于波峰和波谷的间距不同，波幅越长的水翼，前端无空化区域（浅色区域）面积就越大，空泡的分区效应越明显，展向发展受到的限制越强，在尾部也越容易脱落，空化现象减弱。对比图10（b）和图10（d），由于波长的改变，波谷区域的低压区也沿展向随之缩小或增大。波状水翼的波长越小，波谷低压区面积越小，产生的空泡在展向上越难以发展和融合成大型附着型空泡。当受到由于逆压梯度产生的回射流作用时，空泡很容易发生断裂和脱落，故空泡长度也会随着前缘波长的缩小而变短，总体空化现象减弱。

为了更加直观地反映波状水翼对压力脉动的控制效果，在基准水翼和波状水翼中纵截面的吸力侧从空泡初生位置到空泡溃灭位置等比例依次布置了5 个压力测点，对表面压力进行监测。测点的具体位置在图11中给出。

图11 压力测点位置分布Fig.11 Position distribution of pressure measuring points

对监测得到的压力进行快速傅里叶变换（FFT）后得到频域图，如图12 所示，每个水翼的测点位置都在相应的频域图中给出。在图12（a）中，压力谱曲线上出现一个峰值，说明空化发展具有较强的周期性。从P1测点到P5 测点压力系数幅值逐渐升高，对应位置会发生片空泡的断裂和云空泡的溃灭两个重要现象，说明这两种现象是大幅度压力脉动的主要来源。

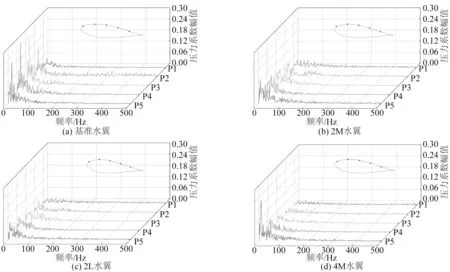
图12 吸力侧压力频域图Fig.12 Frequency-domain diagram of suction side pressure

同样，波状水翼也具有周期性，对比图12（a）和图12（b）～（d），结果表明波状水翼的压力脉动得到了明显抑制，压力脉动幅值显著降低。但规律性与基准水翼类似，都受到了片空泡断裂和云空化溃灭的影响，从而产生大幅度的压力脉动。值得注意的是，4M 水翼靠近尾缘的P5 测点存在一个突出的幅值，这是由于4M 水翼受到前缘构型的影响，空化泡长度较短，只有少部分的空泡能够到达P5 测点位置，故压力较高幅值较大。在不考虑4M 水翼P5测点的前提下，相比于基准水翼，2M 水翼、2L水翼和4M 水翼的压力脉动幅值分别减小了55.3%、67.3%和74.6%，说明前缘波浪构型可以显著降低水翼表面的压力脉动。继而分析不同前缘参数的波状水翼对压力脉动的影响，发现小波幅水翼对压力脉动的控制不如大波幅水翼，2L水翼比2M水翼的压力脉动幅值减小了43.3%；而前缘波长对压力脉动的影响相对较弱，4M 水翼相比2M 水翼的压力脉动幅值只减小了26.9%。综上所述，前缘波浪构型对水翼表面的压力脉动都有一定的控制效果，这种控制效果的规律与对空泡体积的控制相似，随着波幅的增大和波长的减小，控制效果越增强。

3.4 时均流向涡

大量研究表明，非定常空化结构与涡旋运动密切相关。空化泡的产生和发展会产生复杂的涡结构，进而改变流场中的涡量分布。因此，有必要探究空化过程中由于波浪型前缘诱导产生的流向涡的发展规律和流场特征。如图13 所示，对时均流向涡进行0.2c、0.6c和1.2c这3 个截面的可视化分析，并与时均蒸汽体积分数为0.49的等值面叠加显示。结果显示，基准水翼的涡结构碎片化严重，没有明显分布规律，而波状水翼表面则存在明显的对转涡结构。

图13 时均蒸汽体积分数为0.49的等值面和时均流向涡Fig.13 Time-averaged volume fraction iso-surface of 0.49 and time-averaged streamwise vortices

流向涡由于前缘波浪构型的影响，导致相邻的涡旋相向移动，形成一个收敛模式，或者相反运动，形成一个发散模式，分区效应明显。相邻涡的合并导致空泡从水翼表面抬升并限制了涡量在展向的拉伸。在0.2c平面处，可以清楚地观察到这种对转涡结构，且沿流向向上抬升，这种抬升应该与波谷产生的空泡有关，形成的空腔越厚，抬升也越高。考虑不同前缘参数的影响，发现波幅越大或者波长越小，对转涡结构越明显，抬升也越高。在0.6c平面处，由于云空泡溃灭的影响，流向涡的分布开始变得无序，这在图13（a）和13（d）中尤为明显，而图13（b）和13（c）的时均空泡长度较长，还显示为规则的对转涡结构。在1.2c平面处，波状水翼的流向涡也表现出与基准水翼相同的不规则性，这主要是由于水翼尾流的流向涡结构受云空泡溃灭的影响较大，几乎不再受波浪前缘分区效应的影响。

而分析时均空化等值面发现，波状前缘构型的分区效应明显，每个波谷处产生的时均空泡独立存在，沿流向贯通前后，互不干扰。对比分析2M、2L 和2M、4M 两组水翼后发现，大波幅构型限制了空泡在波谷处的展向发展，小波长构型则限制了沿流向的空泡长度，也从另一方面证实了3.3节中对时均表面压力分析得到的结论。