涌浪作用下港内大型集装箱船运动特性数值研究

严明宇，马小舟，郑振钧，董国海

（大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024）

近年来随着造船技术的成熟化和船舶的大型化，港口建设不断向深水区延伸来容纳大型船舶。外海波浪对港口停泊船舶的影响越来越明显［1］。一般来说，外海波浪大部分能量集中在风浪和涌浪组成的短波群（周期＜30 s）上。而港口作为提供船舶靠泊的场所，其防波堤可有效抵挡短波来保护停泊的船舶免受海浪的影响，使泊船具备安全的操作条件。但对于长周期波浪（通常亦称为次重力波，典型周期为30～400 s），由于其波长较长，波速大，具有极强的穿透能力和较大的能量［2］，港口和防波堤的保护效率较低，从而对港口泊稳产生不利的影响［3］。而这类波浪通常由波浪传播近岸过程中短波之间的非线性相互作用所产生［4-5］。理论研究表明，在波高相同的情况下，短波中的涌浪（典型周期为10～30 s）相比于10 s 周期以内的风浪能产生强度更大的次重力波［6］。同时，由于产生的次重力波周期接近港口和船舶运动的固有周期，继而导致了港内泊船发生过度运动的情况［7-8］。由各国规范和国际标准中的极限环境作业条件可知，以最大允许波高作为系泊船装卸作业的泊稳标准所对应的波浪周期范围只针对12 s 以内的短波［9］，这就导致了以波高作为泊稳标准存在一定的局限性。对此在实际工程中，设计方会委托公司或者高校开展研究，考虑较长周期情况下次重力波的影响。譬如，2019年中交二航院联合大连理工大学的产学研合作针对该情况展开了较长周期波浪作用下系泊船舶运动模型试验研究。国外的MARIN 海洋研究中心于2022年启动了HAWA-III计划，旨在研究次重力波对港内泊稳和系泊船的影响。现阶段在研究港内系泊船的泊稳问题时，考虑次重力波浪的影响变得越来越重要。

船舶的安全系泊和装卸作业是港口运营中的重要问题。船舶的泊稳条件除了通过限定作业波高标准来判断，也可以通过船舶最大运动量标准判断。系泊船在不同周期波浪作用下的各自由度运动会表现出不同的特性。国内外不少学者通过物理模型试验研究了波浪周期对系泊船运动响应的影响。Shi 等［10］、沈雨生和周益人［11］分别以LNG 船和散货船为试验对象，研究了横浪作用下波浪周期对系泊船运动响应的影响，均发现了横摇运动量随波浪谱峰周期的增大先增大后减小并在谱峰周期接近船舶横摇固有周期时产生共振响应的规律。然而，对于港内系泊船的物理模型试验，往往只能针对一小块区域进行，如上述物理模型试验中只考虑了泊位码头和系泊船。当需要考虑实际的港口特征（如港口布局和防波堤等）时，会对试验水池的规模尺寸和模型比尺有较为严格的要求。比如，Rosa-Santos等［12］以葡萄牙Leixões港北防波堤内侧石油码头系泊油船为研究对象，在长28 m、宽12 m 的水池以1∶100模型比尺开展了试验，并探讨了波浪周期变化影响下的船舶运动规律。

数值模型由于其高效性和经济性已成为研究复杂形状港口内系泊船运动响应特性的重要手段。为了精确计算复杂形状港口内系泊船的运动，有部分学者建议使用缓坡方程—面元模型包含考虑地形和码头岸壁对系泊船的影响［13-14］。缓坡方程一般是线性的，无法考虑波浪中非线性的影响。Boussinesq方程是目前应用于港口海岸区域上非线性波浪传播模拟的有效工具。Bingham［15］提出了Boussinesq—面元混合模型来预测港内系泊船运动，并通过物理试验验证了该方法的准确性。随后，Pinkster 和Naaijen［16］、Wenneker 等［17］、Van der Molen 和Wenneker［18］基于Boussinesq—面元混合模型的概念开发出类似的数值模型，对不规则波作用下港内船舶的运动响应进行了计算。如今，Boussinesq—面元混合模型已在实际的港口工程设计中得到广泛应用，如澳大利亚Geraldton港［19］和葡萄牙Sines港［20］。

关于系泊船的运动特性研究，物理模型试验由于试验港池的规模有限，在考虑港口的形状特征时存在较大困难。数值模型可以很好地考虑港口形状对系泊船的影响。然而，目前关于港内系泊船特别是大型系泊船的运动响应特性研究较少。因此，以实际港口为例，模拟了涌浪作用下，波浪入射角度和波浪周期对港内大型系泊船运动响应的影响，针对系泊船的泊稳情况探讨了港内系泊船的运动规律和机理。

1 数值计算方法

波浪部分通过基于Boussinesq 方程开发的开源软件FUNWAVE-TVD 模拟［21］。系泊船运动响应则采用MIKE 21 软件计算［22］。文中模型是基于Bingham 的混合Boussinesq—面元模型理论发展而来的。该方法的特点在于波浪部分不通过面元法求解，而是通过Boussinesq 方程波浪模型来获得海岸和港口区域的波浪运动过程，作为船舶时域运动计算的环境荷载之一。

图1展示了文中所用数值模型的计算流程。频域模型采用面元法计算水动力系数。考虑码头岸壁对船舶的影响，在频域内求解船舶的辐射势引起的作用力，其实部和虚部分别对应附加质量Ajk（ω）和辐射阻尼Bjk（ω）。并且分别通过ω→∞和傅里叶逆变换F-1（）的处理可得到时域内的附加质量ajk和迟滞函数矩阵分量Kjk(t-τ)。

图1 数值模型计算流程Fig.1 Flow chart of the numerical model

获得频域模型计算出船舶的水动力系数后，可通过傅里叶变换在时域内求解系泊船舶的运动方程：

式中：Mjk和Cjk为船舶网格计算得到的惯性质量矩阵分量和静水恢复力矩阵分量；ajk和Kjk(t)分别为附加质量系数和迟滞函数矩阵分量；FjD(t)为波浪激励力，包括入射力和绕射力，采用Bingham 的方法计算［15］；Fjnl(t)为缆绳和护舷等对浮体作用的非线性外力；xk(t)表示船舶6自由度运动，见图2。

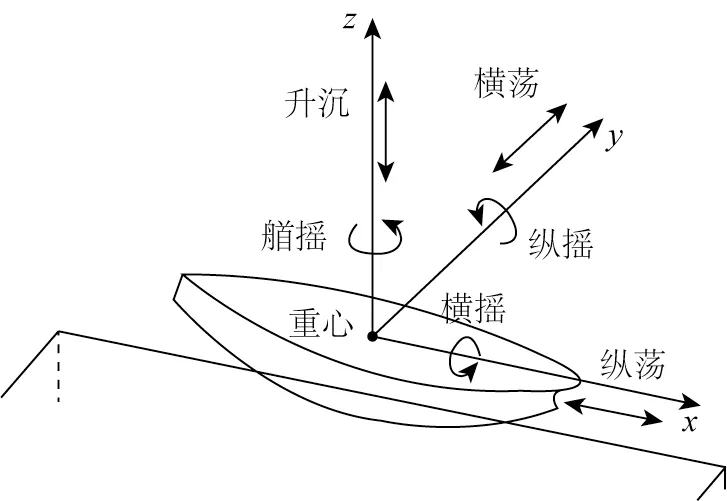
图2 船舶6自由度运动Fig.2 Six degrees of freedom motion of the ship

系泊船时域运动模型的计算需要Boussinesq模型提供无船舶存在的波浪场作为系泊船运动计算的波浪荷载。由于Boussinesq 方程提供的波浪场不考虑船舶的存在，在波浪激励力（等于入射波浪力加绕射波浪力）的求解过程中为了避开船舶影响下绕射势的直接求解，通过Haskind关系［23］将绕射势用入射势和辐射势来表达。因此，需要利用Boussinesq方程模型的结果处理得到入射波浪力和绕射波浪力。

如图1所示，Boussinesq 方程模型提供给系泊船时域模型的输入量为波面高程η和水平通量P，Q。基于线性自由面边界条件，由η得到自由水面处的动压p0和垂向速度分布w0，并通过傅里叶变换F（）得到频域内的p͂0和w͂0。假设浮体所在局部区域地形比较平坦，流场压力和速度均满足双曲函数分布，结合p͂0即可得到流场压力分布，将压力p͂1沿船体湿表面积分得到入射波浪力。

对于绕射波浪力的求解，首先需要获得入射速度势。通过对Boussinesq 方程提供的水平通量P，Q中的水深平均水平速度进行傅里叶变换得到频域内的水平速度u͂，v͂，并利用水深平均速度的定义，对假设的水平流速分布沿水深积分，即可得到用水深平均流速表达的自由面处的水平流速u͂0，v͂0。结合自由面处的垂向速度w͂0求得入射速度势∇ϕ͂I。通过Haskind关系基于入射势和辐射势计算出绕射势。至此，根据绕射波浪力和入射波浪力得到频域波浪激励力F͂jD(ω)，最后将傅里叶逆变换得到的时域波浪激励力FjD(t)和非线性外力Fjnl(t)代入时域运动方程中从而得到船舶运动响应。

在船舶运动的数值模拟中，缆绳对船舶的作用力需要根据缆绳的张紧变形程度结合缆绳的力学特性（即缆绳受力和变形关系曲线）来确定，见图3。对于船舶系缆绳，t时刻缆绳系在码头系船柱上的端点坐标为O（x，y，z），缆绳系在船体上的端点坐标为O1（x1，y1，z1），则缆绳的原始长度为：

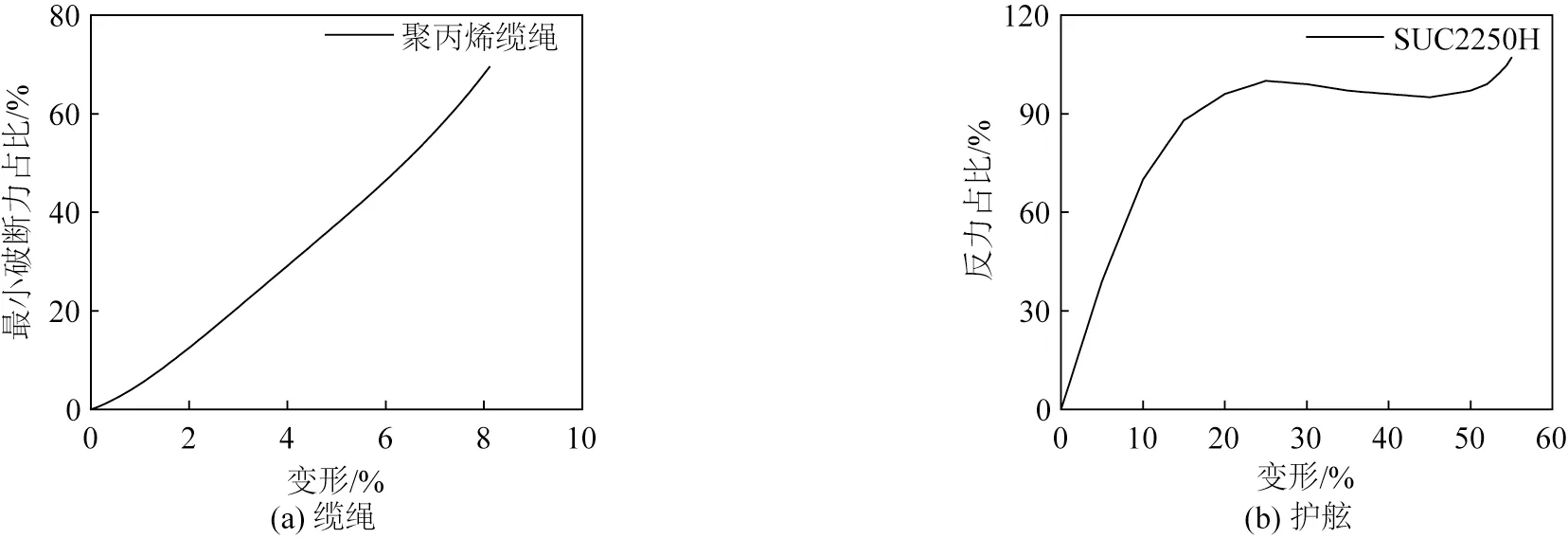
图3 缆绳和护舷的力学性能曲线Fig.3 Force elongation characteristics of mooring line and fender

t+1 时刻随着船体运动到下一个位置，缆绳系船柱上的端点坐标仍为O（x，y，z），在船体上的端点运动到下一个位置，坐标变为O2（x2，y2，z2），缆绳长度变为：

则t+1时刻缆绳的变形长度Δl=l-l1，然后根据缆绳的受力和变形关系即可得到系缆力Fline。

护舷力Ffender包含了护舷反力Ffender，reac和护舷摩擦力Ffender，fric。护舷反力的计算方法与缆绳力相似，假设护舷沿受力方向压缩得到护舷变形量Δf，根据护舷的反力和变形关系即可得到护舷反力，见图3。护舷与船体外壳接触时由于不同材质的影响，会对船体外壳产生一定的护舷摩擦力，由式（4）计算：

式中：μ为护舷的摩擦系数，vel（t）为船体接触点与码头护舷位置点的相对速度。

2 模型设置

斯里兰卡的Hambantota港作为中国推动21世纪海上丝绸之路的重要节点，是距离国际东西航线最近的港口，全球85%的集装箱船途径此地。然而Hambantota 港常年遭受来自印度洋的涌浪影响，存在船舶运动过大而干扰港口作业的情况［24］。因此，以Hambantota港为例，选取主集装箱码头泊位（图4中框出）的系泊船针对泊稳情况展开分析，见图4。

图4 Hambantota港的地理位置和模拟泊位Fig.4 Location and test berth of Hambantota Port

2.1 系泊系统

计算所用船舶为主集装箱码头常见的大型10 000TEU集装箱船。集装箱船的主尺度见表1。

表1 船舶主尺度参数Tab.1 Parameters of principal dimension of the vessel

集装箱船系泊系统中系泊缆采用的是聚丙烯缆绳，缆绳直径80 mm，破断力（MBL）为1 274 kN。靠泊设备为SUC2000H一鼓一板橡胶型护舷，护舷间距为15 m，该型护舷反力为1 893 kN。缆绳和护舷的力学特性参考PIANC［24］，见图2。集装箱船停靠码头作业时的系泊布置采用2∶2∶2∶2（艏/艉缆1∶艏/艉缆2∶艏/艉缆3∶倒缆）的系缆方式，共计16 根缆绳。缆绳的初始预张力为缆绳破断力的10%。集装箱船码头作业时的系泊布置见图5。

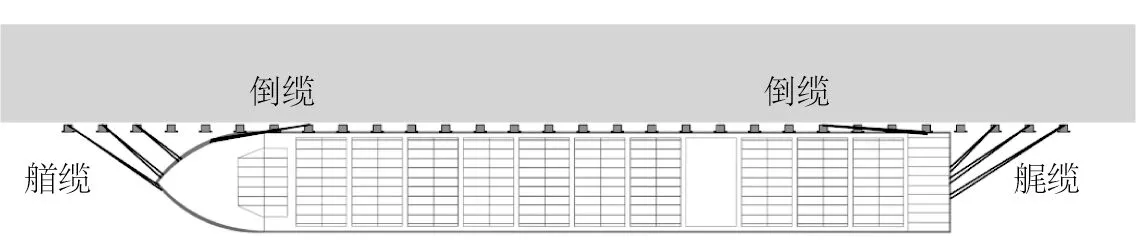
图5 船舶作业时系泊布置Fig.5 Mooring arrangement during ship operation

2.2 波浪模拟工况

入射波况的选取参考Hambantota 港实测波浪数据分析结果［25］，有效波高Hs为1.6 m，入射波浪的谱峰周期Tp范围为10～18 s，港外入射波浪角度为155°和180°，波况的具体参数见表2。采用FUNWAVE-TVD 开源软件模拟系泊船运动所需的波浪场。不规则波的波谱采用Jonswap 谱，谱峰升高因子3.3。需要说明的是，模型所用波谱的高频区域包含了一定的短周期成分，同时Boussinesq 方程模拟的波浪非线性相互作用能产生长周期的次重力波，因此模拟的波浪结果综合体现了短周期波和长周期波的影响［26］。

表2 入射波况参数Tab.2 Parameters of incident wave

Hambantota港波浪场的计算域为3.76 km×3.84 km，网格为dx= dy= 3.0 m。地形是在实地测量的基础上建立起来的。为简便起见，将实际水深大于19 m 的港外水深改为水深19 m 的平底水深。根据设定的入射波况利用Boussinesq 方程模型模拟的港区波浪场如图6 所示，在开放边界处底部和两侧设置海绵层来防止波浪反射回计算域。造波区域布置于计算域的底部，离港口有一定的距离。并且在岸线、防波堤和护岸处设置波浪吸收边界条件来实现部分反射情况。上述波浪模型的参数设置在之前的工作中已经结合现场观测波浪数据得到良好的验证［25-26］。

图6 波浪场数值模型（Tp=14 s, θ=180°）Fig.6 Numerical model of the wave field (Tp=14 s, θ=180°)

3 波浪周期对港内泊位波高的影响

由于系泊船舶的运动是由泊位上的波浪所驱动的，为了更好地理解系泊船舶的运动特性，了解引起船舶运动的港内泊位区域Berth1的波浪变化情况是有必要的（见图6）。

有效波高Hs作为常见的波浪参数通常只能反映外部特征，而不是内部结构。从频域的角度看，波浪各分量的能量是不相同的，对系泊船的作用也不同。因此，文中考虑了不同频段范围内的有效波高，由式（5）、（6）计算。

式中：Hx表示给定频段内的有效波高，Ex表示运动谱S(f)的零阶矩，x表示不同频段，f-和f+表示x频段的频率上下限。这里考虑了两个频段，即f在0.002 5～0.033 0 Hz之间表示低频段的次重力波，对船舶运动有重要影响；f大于0.033 0 Hz 表示高频波段的短波，集中了波浪的大部分波能。f小于0.002 5 Hz 的超低频段长波由于对港池波浪和船舶的水动力影响很小［27-28］，不作考虑。此外，考虑港内泊位选取单一测点计算有效波高时，由于港池振荡模态的影响，可能会在低频波段因为测点位置的不同出现波高差异较大的情况。因此，港内选取泊位区域的平均波高进行定义。

表3和表4分别展示了泊位区域的有效波高，由表可知，180°浪向下的所有频段波高整体小于155°浪向下的波高。这主要是因为180°浪向下波浪由于防波堤的影响主要通过绕射传播进港内，而155°的波向偏向于港口航道方向，防波堤起到的作用较小。还可以看到，低频段的波高Hlf随波浪周期的增加而增大，而高频段的波高Hhf变化趋势较小。

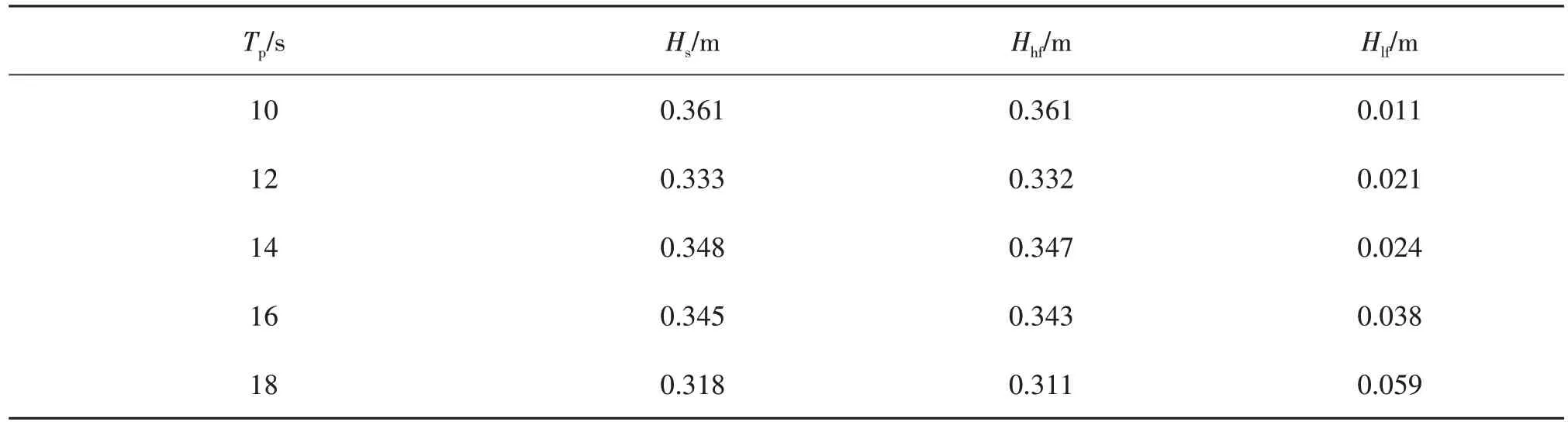
表3 180°浪向下泊位的有效波高Tab.3 Significant wave height at berth under 180°

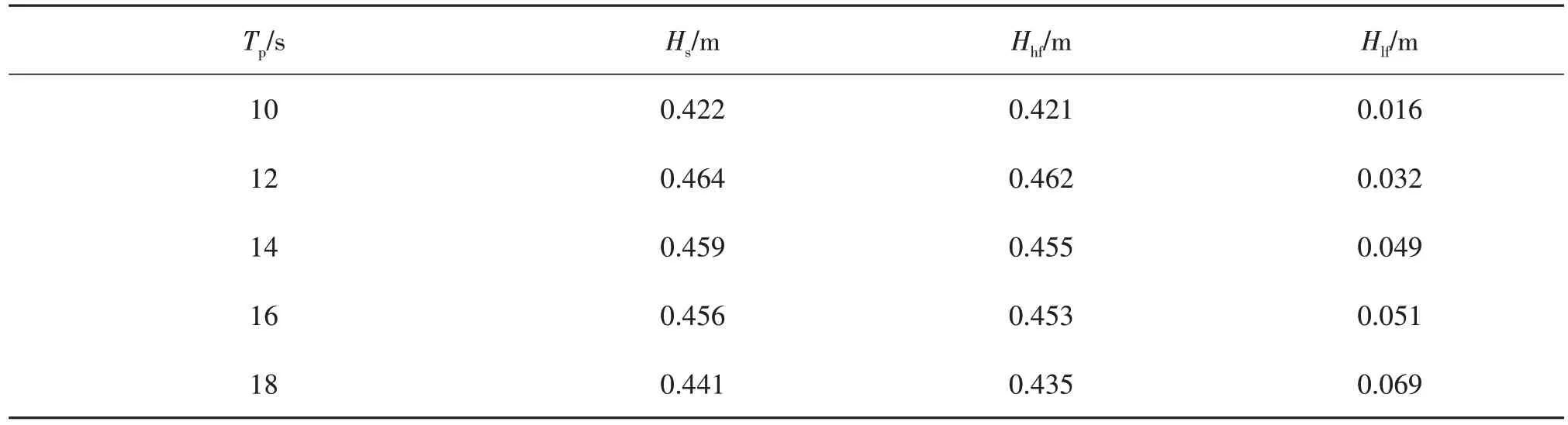
表4 155°浪向下泊位的有效波高Tab.4 Significant wave height at berth under 155°

此外，除了系泊船的运动量作为衡量船舶泊稳的重要指标之外，泊位码头前的允许波高也是判断泊稳的标准之一。基于《基于国内外规范和标准的海港工程总平面设计指南》［9］中船舶装卸作业的允许波高相关标准可知，集装箱船正常作业的Hs为0.5 m。泊位的最大波高为0.464 m，满足集装箱的正常作业条件。

4 波浪周期对船舶运动响应的影响

4.1 计算结果统计

由图3 的计算流程可知，船舶的频域模型提供的水动力结果经过傅里叶变换后，代入到式（1）中可以用来求解船舶的运动响应。图7 为集装箱船频域模型的水动力系数结果，图8 为180°浪向下（迎浪）的纵荡方向波浪激励力和90°浪向下（横浪）横荡方向波浪激励力。图9 为船舶在180°外海入射浪向和谱峰周期为18 s时的纵荡和横荡运动时间序列。

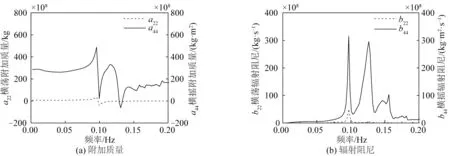
图7 集装箱船的水动力系数Fig.7 Hydrodynamic coefficient of the container ship

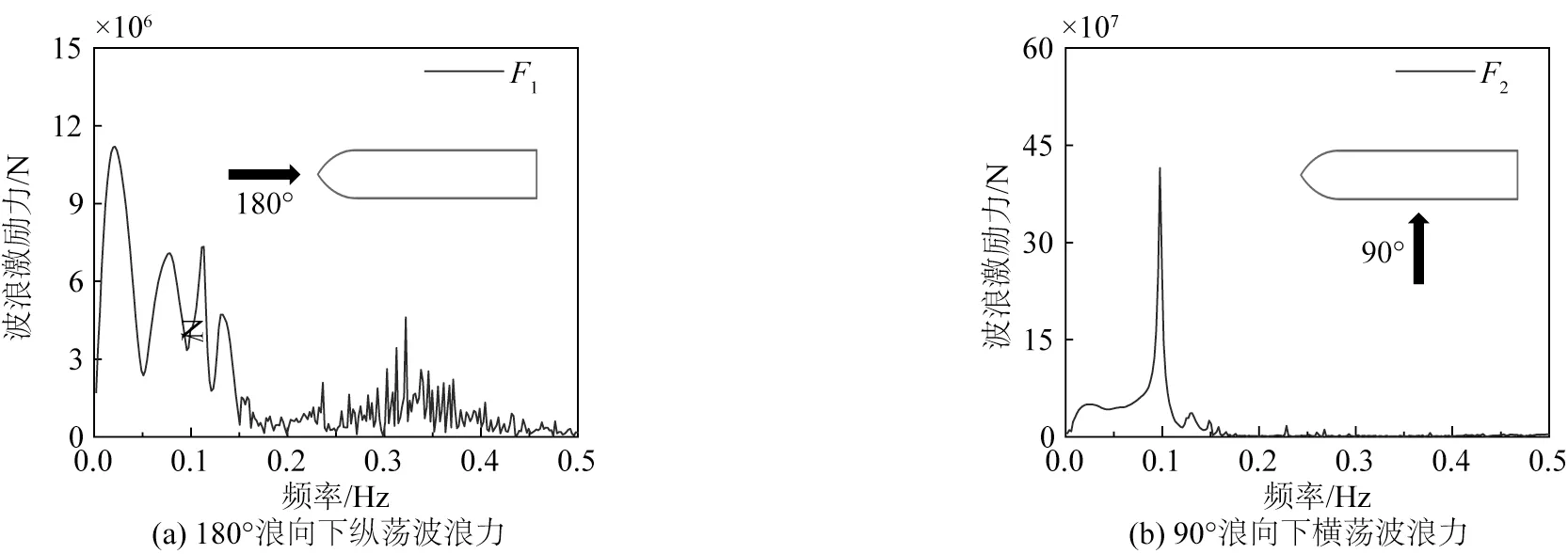
图8 集装箱船的波浪激励力Fig.8 Wave exciting forces of the container ship

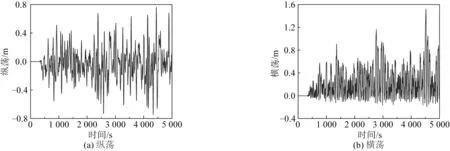
图9 船舶运动的时间序列Fig.9 Time series of ship motions

4.2 不同浪向下波浪周期对船舶运动量的影响

对于系泊船舶运动量的统计，PIANC［29］建议以系泊船舶的初始位置为参考，采用跨零点法对船舶6自由度运动的时间序列进行时域分析，峰—峰标准来识别每个单独的运动（除了横荡，采用零—峰标准）。跨零法的基本概念在图10 中得到说明。在由两个向下跨零点定义的周期内，纵荡、升沉、横摇、纵摇和艏摇运动的振幅为a1+b1，a2+b2，···，aN+bN。通过对识别出来的N个振幅进行从大到小排列，取最大的N/3 个振幅的平均值，记为有效运动量。对于横荡运动，由于码头护舷的影响，船舶主要向偏离码头的方向横向运动，这就导致横摇运动中一侧的运动幅值远小于另一侧。因此，选取偏大一侧的幅值进行有效值统计并记为横荡的有效运动量。

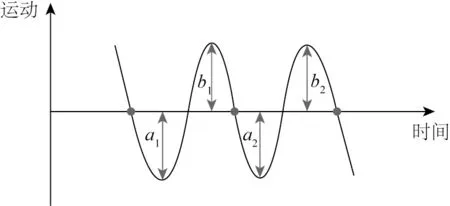
图10 分析运动时间序列的跨零点法的定义Fig.10 Principle of zero-crossing technique for analyzing motion time series

按照上述统计方法，不同浪向下波浪谱峰周期对船舶6 自由度运动量的影响如图11 所示。可以看出，与180°浪向下船舶运动相比，155°浪向下的船舶6 自由度运动量要偏大。这是由155°浪向下泊位的波高整体偏大所导致的。此外，不同浪向下的船舶6自由度运动量随谱峰周期变化的规律基本相同，即船舶的各运动量随谱峰周期的增大而增大。其中，纵荡运动量在不同浪向下随谱峰周期变大的增长趋势均最为显著。

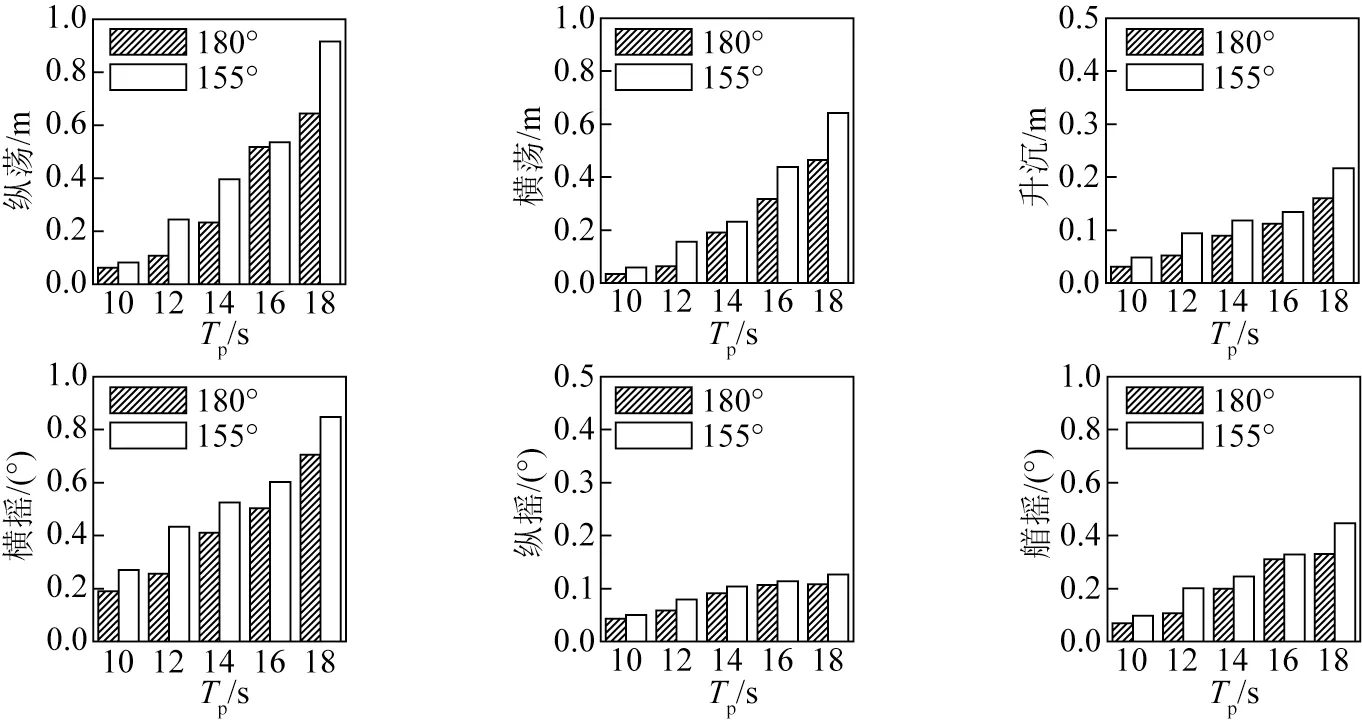
图11 波浪谱峰周期对船舶运动量的影响Fig.11 Influence of peak wave period on ship motions

根据集装箱船的装卸作业允许有效运动量标准（表5）对船舶运动进行了评估［25］，该标准为集装箱船停泊码头时，装卸作业效率为95%时的允许有效运动标准，可以用来衡量港内停泊集装箱船的运动。95%的限制效率对应的操作是，由于波浪流等环境荷载作用，集装箱船的运动导致起重机装卸集装箱船的累计延迟不超过5%的时间。并且95%的作业效率是集装箱码头的运营商可以接受的限制效率。结合图11可知，两个入射浪向下的集装箱船纵荡运动在16 s 和18 s 的谱峰周期下均超出了0.4 m。155°入射浪向下的横荡运动在16 s和18 s周期下超出了0.4 m，180°浪向下的横荡运动只在18 s周期下超出了标准值。艏摇运动超出限制值的情况则与纵荡运动相同。因此，可以看出，超出装卸作业效率95%的集装箱船允许运动标准值的主要运动是水平运动（纵荡、横荡和艏摇）。此外，结合前文波高泊稳分析结果可知，考虑正常作业的允许波高标准值不足以确定系泊船的正常作业条件。

表5 装卸效率95%的集装箱船允许有效运动标准Tab.5 Allowable significant motion criteria for container ships with 95% (un)loading efficiency

此外，基于运动的时域统计结果可知，在波浪周期较大时，港内泊船的水平运动极易超出运动标准值并影响装卸作业效率。因此有必要了解水平运动对集装箱船装卸作业的影响。

对于纵荡运动而言，如果船舶沿着码头的运动偏大，理论的解决方案是沿着码头移动起重机来配合装卸，但由于人为因素使得多个起重机的作业过程难以同步，在实际装卸过程中是不现实的。因此，如果纵荡运动过大，船上的某一排集装箱可能会移动到起重机的范围之外，从而直接导致装卸效率的降低更甚至作业停工。对于横荡和艏摇而言，通常运动的周期性相比纵荡来说偏小，当船舶离开或者偏向码头移动过大，操作人员能够依靠起重机功能和作业经验来减少装卸效率的下降。而时域运动结果显示船舶的水平运动量随着波浪周期的增大而增大，并且以纵荡运动量的增长趋势和超出标准值的量最为显著。由此可见，波浪周期越大，船舶水平运动对装卸作业效率的影响越明显。

4.3 船舶运动频域特性分析

船舶运动的时域分析提供了不同运动的统计结果，而频域分析则可以反映船舶各运动在不同频率范围内的能量分布情况。频域分析采用离散傅里叶变换，以提供频域内有用的信息从而了解船舶运动的频率特性。选取代表性周期10 s和18 s在不同浪向下的频域结果进行展示，见图12。为了更好地了解船舶运动频域信息中的分布情况，参考短波和次重力波等不同频率范围，通过设置两个频率（f=0.002 5 和f=0.033 0）对运动频谱进行划分。

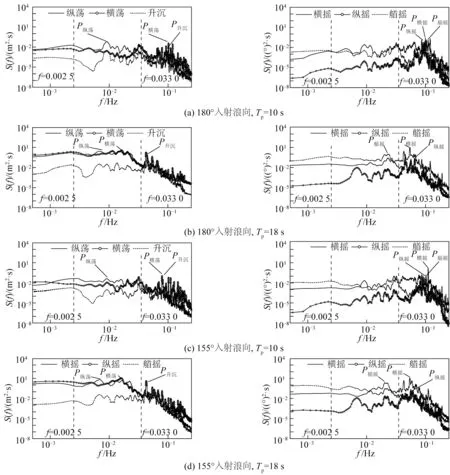
图12 不同浪向下船舶运动频谱分析Fig.12 Spectrum analysis of ship motion under different wave directions

由图12（a）可知，船舶在入射浪向为180°，谱峰周期为10 s时，纵荡运动表现出明显的低频特性，其峰值频率处在低频段，其余运动的峰值频率则处在高频段，并且主要集中在10 s谱峰周期的波浪特征频率附近。这也表明了10 s周期下的船舶运动除纵荡外，其余自由度的运动均以波频运动为主。

当入射浪向为180°，谱峰周期为18 s时（见图12（b）），船舶的纵荡运动依旧表现出明显的低频特性。与10 s周期相比，横荡和艏摇运动的峰值频率则转移到低频段。而升沉、横摇和纵摇运动的频谱峰值也还是在高频段，且主要集中在18 s的特征波浪频率附近。由此可以看出，船舶的垂直运动（升沉、横摇和纵摇运动）表现出主要由短波中波浪激励频率主导的波频运动特性。对155°浪向对应的船舶运动进行了频域分析，分析结果与180°的规律相似。

图12的频谱分析结果主要展示了峰值频率的分布情况，图中可知，除了峰值频率的所在频段，其他频段也出现一定的频率分布。为了进一步了解船舶运动在不同频段内的能量集中情况。参考波浪有效波高的处理公式进行各运动频谱的频段能量计算，见式（7）。

式中：rx为给定频段内能量Hx与总频谱能量Hall的比值，表示不同频段能量的占比。

表6 和表7 分别列出了180°和155°浪向下船舶6 自由度运动的各频段能量占比平均值，其中rˉlf为低频段，rˉhf为高频段。从表6中可以看出，船舶的水平运动（纵荡、横荡和艏摇）中，低频段能量明显高于高频段能量。其中纵荡运动的低频段能量占比最高，且能量几乎都在低频段范围内。而横荡和艏摇运动的各频段能量占比情况相似，即除了低频段的能量最多外，高频段也集中了一定的能量。对于船舶的垂向运动（升沉、横摇和纵摇），高频段的能量占比远远高于其他频段。表7表现出的规律与表6相似。

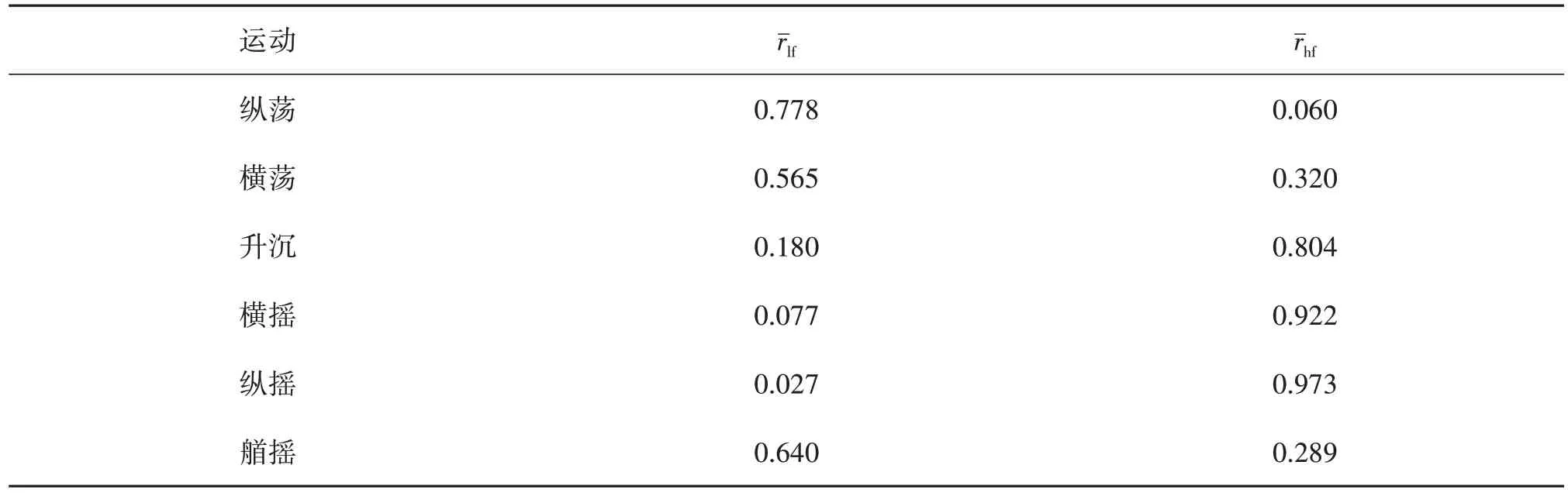
表6 船舶运动的各频段能量占比平均值（180°浪向）Tab.6 The average ratio of energy in each frequency band of ship motion (180°)

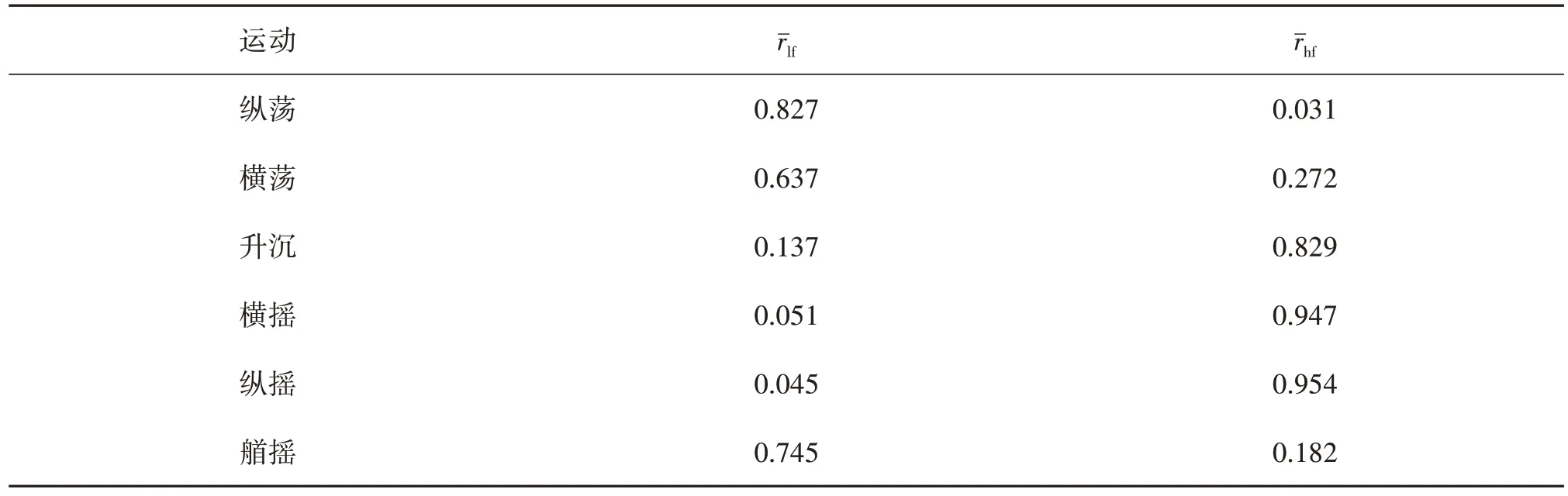
表7 船舶运动的各频段能量占比平均值（155°浪向）Tab.7 The average ratio of energy in each frequency band of ship motion (155°)

结合图12的频谱分析结果可知，波浪周期较大的情况下，船舶的水平运动（纵荡、横荡和艏摇）表现出主要由次重力波主导的低频运动特性。其中的纵荡运动，由于其运动能量几乎都集中在低频范围内，因此其表现的低频运动特性最为明显。然而由于横荡和艏摇运动在高频段存在一定的能量，并且在波浪周期较小时，两个运动的频谱峰值均主要集中在谱峰周期的波浪特征频率附近，因此表现出了一定的波频运动特性。对于不同周期下的垂直运动（垂荡、横摇和纵摇），由于其高频段能量的占比相对低频段较高，且峰值频率均集中在波浪特征频率附近，因此垂直运动特性没有受到周期变化的影响，表现出由短波主导的波频运动特性。

5 结 语

以实际港口为例，模拟了涌浪作用下不同入射角度和波浪周期影响的港内大型系泊船的运动响应，针对系泊船的泊稳情况探讨了港内泊船的运动规律和运动特性，主要结论如下：

1） 所有模拟工况下的泊位有效波高均小于波高的泊稳标准值0.5 m，由于155°浪向下的港外防波堤掩护效果较差，港内泊位的波高整体大于180°浪向。此外，波浪周期的变化对港内泊位有效波高的影响并不显著，低频波高随波浪周期的增加逐渐增大。

2） 对于运动限制标准，两个浪向下的纵荡运动在16 s 和18 s 的谱峰周期下均超出了0.4 m、155°入射浪向下的横荡运动在16 s 和18 s 周期下超出了0.4 m、180°浪向下的横荡运动只在18 s 周期下超出了标准值。艏摇运动超出标准值的情况则与纵荡运动相同。此外，不同入射浪向下的船舶6 自由度运动量随谱峰周期变化的规律基本相同，即船舶的各运动量随谱峰周期的增大而增大。其中，纵荡运动量的增长趋势均最为显著。

3） 涌浪周期较大的情况下，船舶的水平运动（纵荡、横荡和艏摇）表现出主要由次重力波主导的低频运动特性。特别是纵荡，其运动能量几乎都集中在低频段，因此其表现的低频运动特性最为明显。横荡和艏摇运动由于高频段能量的存在使其在波浪周期较小时也能表现出一定的波频运动特性。而垂直运动（垂荡、横摇和纵摇） 则主要表现出由短波主导的波频运动特性。