沙质海岸沿岸输沙率计算方法研究进展

王宁舸，韩 信，孙 波，辛文杰，张 弛，陈大可

（1.南京水利科学研究院，江苏 南京 210029；2.河海大学，江苏 南京 210098）

根据中国《港口与航道水文规范》（JTS 145—2015）［1］，广义上的沙质海岸沉积物中值粒径一般大于0.10 mm。进一步细分，一般可分为通俗意义上的沙质海岸（中值粒径一般小于2.00 mm）和卵砾石海岸（中值粒径一般大于2.00 mm）。波浪是这类海岸泥沙运动的主要动力，波浪作用下的沿岸与向岸—离岸输沙是控制沙质海岸岸线及岸滩演变的主要因素，其中尤以沿岸输沙为重，表现为海岸线长期前进或后退，历时可达数年、数十年乃至百年以上。在海岸带资源的开发利用中，沙质海岸工程建设与岸滩修复等均与沿岸输沙控制下的岸滩长期演变密切相关［2］，因此沿岸输沙问题得到业界广泛关注。

沿岸输沙是波浪动力与岸滩之间相互作用的结果，由于海岸环境多样复杂，能够快速准确地预测研究区域沿岸输沙能力非常关键。目前，采用沿岸输沙率计算公式预测和通过数学模型计算的方法，已成为研究沙质海岸沿岸输沙问题的两项重要手段。近数十年来，数学模型经历快速发展已得到广泛应用，但由于破波带、波浪上爬带的水沙动力学机制极为复杂，沙质海岸数学模型对这些区域水沙动力过程的描述至今尚未成熟。当研究区域无工程案例时，数学模型无法通过现场岸线与岸滩演变实测资料进行复演，难以准确判断该区域的输沙情况，这使得数学模型在快速准确预测方面具有明显的局限性。20世纪30年代以来，经历近百年的发展，沿岸输沙率计算公式得到众多学者的深入研究并不断完善，成果丰富。相比于数学模型计算，采用沿岸输沙率计算公式预测可不受研究区域有无工程案例的限制，在一定程度上弥补了数学模型计算的不足。与此同时，凭借着简洁高效的突出优势，沿岸输沙率计算公式至今仍是快速判断研究区域沿岸输沙强度不可或缺的重要手段。

以往多位学者对沿岸输沙率公式研究进行过述评，如黄建维［3］、孙林云［4］、白玉川等［5］。这些述评或从研究方法出发［3-4］，或从输沙的分布形式考虑［5］，回顾了沿岸输沙率计算公式代表性成果。在前人述评成果的基础上，结合近些年国内外新的研究成果，延续按照研究方法进行分类，重点对波浪作用下沿岸输沙率计算公式的研究和发展过程进行再次回顾，对各项成果的理论基础、考虑因素、资料来源等方面进行再探讨，对未来可继续深化研究的内容作出展望。

1 能量原理计算方法

20世纪60年代以前，沿岸输沙问题研究处于刚起步的探索阶段。人们直观地认为沿岸输沙是沿岸波能的函数，1933年丹麦工程师Munch-Peterson指出，可以通过测定单位波峰线长度上波能流的沿岸分量近似预报沿岸输沙率的方向和总量［6］，从而最早将沿岸输沙与波能建立起了联系，即早期的波能流法。由于缺乏必要的波浪数据，Munch-Peterson 实际上应用了风速、风频率和海上吹程来间接估算沿岸输沙率。真正开始尝试将沿岸输沙率与波能建立经验关系要追溯到后来的斯克利普斯（Scripps）海洋研究所［2］、Watts［7］、Caldwell［8］和Savage［9］等的研究，其中Savage［9］汇总了当时各种现场调查和室内试验数据，建立了体积沿岸输沙率计算公式，并被美国陆军工程兵团海岸研究中心（USACE）编入了1966年版的Shore protection manual，即CERC公式的早期形式。这类公式的建立方法即波能流法，公式的一般形式为：

式中：Q为体积沿岸输沙率，m3/s；K为经验系数；Pl为单位岸线长度上破波波能流的沿岸分量，N/s；E为单位波峰线长度的破波波能，kg/s2；Cg为破波波能传播速度，m/s；θb为破波波向与岸线的夹角（以下简称为“破波角”）。从式（1）和（2）可以看出，波能流法原本是个纯经验方法，公式的量纲并不和谐，造成物理意义不明确。

1963 年，Bagnold［10］提出了能量输沙原理，假设波浪维持着泥沙往复运动但并不产生净输沙，任意一种水体净流动叠加于波浪之上则形成泥沙净输移。Inman 和Bagnold［11］将Bagnold［10］的能量输沙原理应用于海岸泥沙，从而最早揭示了沿岸输沙机理，即“破波掀沙、沿岸流输沙”的物理机制。此外，针对式（1）的量纲问题，Inman 和Bagnold［11］建议用浮容重输沙率Il代替体积输沙率Q，使得公式量纲和谐，建立的沿岸输沙率公式见式（3）。这一系列举动推动沿岸输沙率公式研究进入到一个新的发展阶段。

式中：Il为浮容重输沙率，N/s；-Vl为破波带平均沿岸流流速，m/s；umb为破碎波的近底波浪水质点最大轨迹速度，m/s。

1970年，Komar和Inman［12］采用在美国加利福尼亚银滩和墨西哥埃尔莫雷诺海滩得到的波浪、沿岸流和输沙率同步观测数据，分别对纯经验方法的波能流公式与Inman 和Bagnold 公式［11］进行了检验和率定，显示这两种方法对实测资料均吻合较好。Komar 和Inman［12］还给出了破波带平均沿岸流计算公式，见式（4）。公式形式与Longuet-Higgins［13］推导的平均沿岸流理论解基本一致。研究表明，当Inman 和Bagnold 公式［11］中的沿岸流-Vl采用式（4）计算时，基于纯经验方法和能量输沙原理的两个公式具有一致性，从而在理论上证明了纯经验方法的合理性，使波能流法具有了能量输沙的理论基础。Komar 和Inman［12］率定得到的沿岸输沙率（式（5））被USACE收录在后续更新版本的Shore protection manual［14］中，作为改进的CERC公式进行推荐。

式中：Il为浮容重输沙率，N/s；当波能流采用均方根波高计算时，K取0.77；当波能流采用有效波高计算时，K取0.39。

波能流法被赋予理论意义后，CERC公式［14］成为了半经验半理论公式，沿岸输沙率与波能流之间通过经验系数K建立关系。CERC 公式［14］所反映的物理含义是，对于任意强度的波浪能量，可以计算该波能所具有的输沙能力，但该公式仅与波能建立了联系，还未反映出泥沙粒径、岸滩坡度、波浪周期、波陡、破波类型等其他因素的影响，导致公式的预测可靠性较低，K的取值问题一直以来存在疑问。许多学者在检验CERC 公式［14］时，依据自身获取的数据资料对K值进行了再率定，结果差异很大，取值范围在0.05～0.92［15-18］，因此系数K不应该是一个简单的常数，可能是包含多种影响因子的函数关系式。值得一提的是，Komar 和Inman［12］采用现场实测资料率定得到的系数K比以往的率定值增大约一倍，这是删除了原来室内试验资料点的缘故［4］。图1 为Komar 和Inman［12］对CERC 公式［14］的检验，当采用以往室内原型沙试验资料进行检验时，公式预测值普遍偏大，这既说明了该公式在反映不同动力环境方面的局限性，又表明该公式不能同时符合现场和室内两种尺度的沿岸输沙基本规律。

图1 Komar和Inman对CERC公式检验Fig.1 Komar and Inman's test for the CERC formula

CERC 公式［14］的确存在明显的局限性，但其最重大的意义在于，CERC 公式是经验与理论相结合的首个成果。凭借着物理意义明确、公式结构简洁、便于使用等特点，CERC公式［14］是目前为止使用率最高、受检验最多的沿岸输沙率公式，并且其K值问题进一步推动了沿岸输沙率公式这一研究方向的发展。许多学者针对系数K的表达形式陆续开展了更深入的研究工作，以期改进CERC公式［14］，扩大适用范围。

1966年，Larras［19］通过室内原型沙试验提出了一个纯经验公式，考虑了泥沙粒径和波陡对沿岸输沙的影响。赵今声［20］借鉴了Larras［19］对泥沙粒径影响的表达形式，并与波陡进行乘积，再继续沿用波能流法表达形式，本质上可以归为对CERC 公式［14］的改进。赵今声公式［20］见式（6），该公式相当于在CERC 公式［14］的系数K中进一步考虑了泥沙粒径和波陡的影响。

式中：Q为体积输沙率，m3/s；D50为泥沙中值粒径，mm；H0为深水波高，m；L0为深水波长，m。

重点研究泥沙粒径影响还有Swart［21］、USACE［22］和Del Valle 等［23］，他们对CERC 公式的系数K进行了改进，表达形式分别见式（7）～（9）。其中Swart［21］和Del Valle 等［23］的公式直接与泥沙粒径建立了关系，USACE［22］的公式通过泥沙沉速以反映粒径的影响。这3 个公式均表明，一般而言沿岸输沙率随粒径增大而减小。

式中：Hb为破碎波高，m；ωs为泥沙沉速，m/s；g为重力加速度，m/s2。

除泥沙粒径影响外，波浪破碎类型也非常重要。在二十世纪六七十年代，业界对于破波类型的影响已开始关注，并且建立了能够代表破波类型的判数［24-25］，即伊利巴伦数，见式（10）。第一次将破波类型判数引入了CERC 公式［14］系数K的是Kamphuis 和Readshaw［26］，他们根据室内原型沙试验并结合量纲分析方法，建立了系数K与破波类型的定量关系式，见式（11）。随后，Philip［27］根据试验结果，也验证了经验系数与破波类型具有较强的相关性，并得到经验关系，见式（12）。Özhan［28］和Mil-Homens 等［29］提出的表达形式也属于此类，其中Özhan［28］是对坡度为1∶10 的岸滩进行了沿岸输沙试验，并且考虑了崩破波、卷破波和激破波3 种破波类型，但受限于缺少不同岸滩坡度的试验结果，最终没有与破波类型建立关系，而是得到K与深水波陡的关系式（13）。Mil-Homens等［29］采用Bayram等［30］总结的现场和室内原型沙试验资料，通过对比多个无量纲参数，也选择了波陡与CERC 公式［14］中系数K建立改进关系，改进的表达式见式（14）。这4个关系式定性均表明，输沙率随破波类型判数的增大而增强，定性合理。

式中：Ir为破波类型判数；Hsb为破碎波有效波高，m；m为岸滩坡度。

Bagnold［10］的能量输沙原理具有明确的“破波掀沙、沿岸流输沙”物理机制，赋予了波能流理论依据，基于该理论建立的公式相对简洁高效，已得到业界广泛研究和应用。除前文所述的CERC 公式［14］及各类改进公式外，还有赵子丹公式［31］、Brampton和Motyka公式［32］、Walton和Bruno公式［33］和Madsen公式［34］等。不过该原理的应用更多面向推移质，并且未考虑泥沙粒径因素，泥沙的影响需要通过建立经验关系来获得，缺乏理论推导。

1973 年，Dean［35］采用与河流输沙重力理论相似的悬浮功模式，假定破波带总波能流中有比例K用于克服泥沙沉降做功，保持泥沙悬浮，再由沿岸流产生输沙，从而使能量输沙原理有了进一步发展，并应用于悬移质输沙。Dean 公式［35］形式见式（15）和（16），该模式通过理论推导可自然地引入泥沙沉速，从而与泥沙粒径挂钩。

式中：Qm为质量输沙率，kg/s；Scp为破波带平均悬移质含沙量，kg/m3；Al为平均水位下破波带水体断面面积，m2；ρs为泥沙颗粒密度，kg/m3；ρ为水密度，kg/m3。

基于悬浮功模式的能量输沙原理使得沿岸输沙率公式研究得到了进一步发展，将以往以推移质输沙为主的理论推广至悬移质输沙，适用于相对更常见的、通俗意义上的沙质海岸，尤其是这类海岸在较强动力作用下发生强输沙时的场景。

20 世纪70 年代，中国援建毛里塔尼亚友谊港。以此为契机，国内沙质海岸泥沙运动研究领域得到极大的推动和发展，积累了一批有价值的成果。1976 年，陈子霞［36］在Dean 悬移质输沙率公式［35］的基础上，进一步考虑了推移质输沙，公式见式（17）。陈子霞［36］采用努瓦克肖特瓦尔夫港1975—1976 年5 组推移质和7 组悬移质的现场水文泥沙观测资料，分别求得推移质输沙系数K0= 1.59 × 10-5，悬移质输沙系数Ks= 2.25 ×10-3。从比值上看，推移质输沙比例小于1%，泥沙运动以悬移质输沙为主。可见，对于毛里塔尼亚友谊港这类强输沙海岸而言，沿岸输沙定性上以悬移质运动为主。

式中：Qm为质量输沙率，kg/s；Qs为悬移质质量输沙率，kg/s；Qb为推移质质量输沙率，kg/s。

Bailard［37］结合了Bagnold［10］能量输沙原理和基于悬浮功模式的能量输沙原理，借助现场和室内原型沙试验资料，建立了包括悬移质和推移质在内的单宽输沙率公式，再沿断面积分得到与CERC 公式［14］相同的形式。与CERC 公式［14］相比，相当于系数K综合考虑了破波角、波浪临底流速和泥沙沉速的影响，见式（18）。其中，波浪临底流速与泥沙沉速的比值即泥沙悬浮因子，在一定程度上反映了波浪掀沙与泥沙沉降之间的强弱关系。

1992 年，孙林云［4］在总结前人研究的基础上，也从悬浮功模式的能量原理出发，辅以量纲分析法，建立了以悬移质输沙为主的沿岸输沙率公式，提出了破波类型对泥沙悬浮和破波沿岸流的影响，公式见式（19）。孙林云［4］采用的资料是友谊港1983—1984年共28组现场水文泥沙观测资料，该资料是在当时友谊港新建成的透空栈桥断面上基于水文法观测得到的强输沙海岸悬移质输沙资料。从公式形式上看，该公式同时考虑了破波类型和泥沙悬浮因子的影响，其中破波类型又涵盖了波高、波浪周期和岸滩坡度的影响及三者之间的相关关系，泥沙悬浮因子反映了波浪掀沙与泥沙沉降之间的强弱关系。与以往各项能量法公式相比，孙林云公式［4］第一次较全面地考虑了波浪动力、岸滩坡度和泥沙等因素的影响，物理意义明确。公式表明，输沙率随破波类型数增大而增大，定性合理。该公式分别于1993 年和2004 年陆续在国内外学术会议上进行了交流［37-38］。针对孙林云公式［4］的适用性问题，郭天润［39］采用室内轻质沙输沙试验资料进行了检验，表明该公式可同时适用于现场原型强输沙尺度和室内轻质沙模型尺度的输沙预测，符合两种尺度下沿岸输沙统一规律，检验结果见图2［39］。

图2 孙林云公式对友谊港现场实测资料和郭天润室内轻质沙资料的检验Fig.2 Test for the Sun Linyun formula based on the field data of Friendship Port and indoor light weight sand data of Guo Tianrun

式中：Q为体积输沙率，m3/s；a为泥沙孔隙率。

2007 年，Bayram 等［30］基于6 套现场与试验资料，采用基于悬浮功模式的能量输沙原理建立了沿岸输沙率公式，公式见式（20）～（23）。Bayram 公式［30］建立的基本理论和总体思路与孙林云公式［4］相似，只是在关键参数的选择上有所不同。Bayram 公式［30］最大的特点是在沿岸流流速Vl和经验系数ε中考虑了Dean 提出的平衡剖面及判数，其中在推导沿岸流流速时引入了Dean 平衡剖面函数关系式，从而考虑了岸滩剖面形态的影响；在率定经验系数ε时，通过敏感性分析与Dean数建立了关系式。最终，Bayram 公式［30］中的影响因素包含了波高、周期、岸滩形态和泥沙沉速等，考虑因素较为全面。

式中：Q为体积输沙率，m3/s；γb为波浪破碎指标；cf为摩阻系数；A为与Dean 剖面相关的形态参数；TP为谱峰周期，s。

与孙林云公式［4］相似，Bayram 公式［30］的显著优点是理论基础可靠、物理意义明确、考虑因素较全面，但其在反映周期影响方面定性存在一些问题。参考Kamphuis 和Readshaw［26］、Philip［27］、Özhan［28］和孙林云［4］等学者提出的计算公式，以及Wang等［40］室内原型沙沿岸输沙试验成果，周期的影响在定性上均表现为周期越大则破波类型数越大，沿岸输沙越强。Mil-Homens 等［29］对多个沿岸输沙率公式进行了改进，也指出沿岸输沙率强度与周期大小主要呈现正相关关系。因此，Bayram 公式［30］对于周期影响的考虑在定性上与通常认知相悖。如果再仔细观察Bayram 对ε［30］建立关系时的散点图，可以发现数据点基本集中在小输沙量级，大输沙量级的离散程度较大，拟合效果不佳（见图3），因此系数ε中考虑的参数可能还有更好的选择。Mil-Homens［29］对Bayram 公式［30］进行改进时，最终选择了波陡与系数ε建立关系，改进后的系数ε表达式见式（24）。Mafi等［41］采用现场和试验数据也改进过Bayram 公式［30］，从泥沙起动的角度建立了系数ε与希尔兹数θ的关系，但牺牲了对周期的考虑。

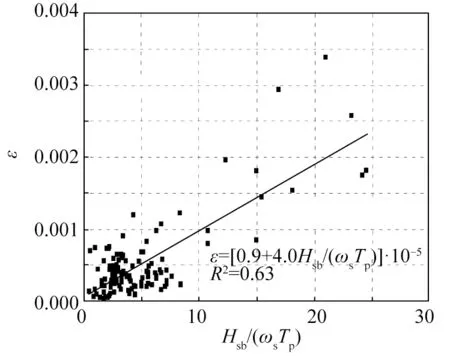
图3 Bayram公式中系数ε建立关系散点图Fig.3 The scatter plot of the coefficient ε in Bayram formula

不论是波能流法，还是Bagnold［10］的能量输沙原理，亦或是基于悬浮功概念的改进模式，本质都是将沿岸输沙与波浪能量建立关系，因此统称为能量法或能量原理。能量法物理意义明确，公式结构简洁，并且已有较多的现场和室内试验资料作为依据，因此可信度相对较高，应用最为普遍。

2 量纲分析计算方法

量纲分析法属于经验方法的一种类型，主要在公式中考虑如波高、周期、破波角、泥沙粒径、岸滩坡度等各种影响因子以及如破波类型数、波陡等具有物理意义的无量纲参数，采用实测资料对各项参数进行敏感性、相关性分析。采用量纲分析法建立公式的如佩什金—马克西米乌克—阿维林［2］、Kamphuis 等［42-43］、Van Hijum 和Pilarczyk［44］、Chadwick［45］、Arcilla 等［46］、Van Der Meer 等［47-49］、Van Wellen 等［50］、Van Rijn［51］和Shaeri等［52］，其中最具代表性的是Kamphuis等［42-43］。

Kamphuis 等［42］的早期公式见式（25），该公式建立过程中考虑了破波类型的影响，但可惜最终表达式中周期T被抵消了，定性上存疑。1991 年，Kamphuis［43］采用室内原型沙试验资料，在其1986 年公式［42］的基础上，优化了部分无量纲参数的表达形式，使得周期T的影响被重新考虑，公式得到完善，见式（26）。此外，Kamphuis［43］还加入了现场实测资料对公式进行检验，表明该公式可同时适用于现场和室内试验两种尺度（见图4）。Kamphuis 公式［43］较全面地考虑了波高、周期、岸滩坡度和泥沙粒径等多种因素的影响，并且各影响因素所反映的规律定性合理，但通过分析不难发现，包括其早期公式形式在内，Kamphuis两个阶段公式的量纲并不和谐。

图4 Kamphuis公式对现场和室内原型沙实测资料的检验Fig.4 Test for the Kamphuis formula based on the field and indoor prototype sand data

式中：Ql为浮质量输沙率，kg/s。

Schoonees 和Theron［53］对Kamphuis 公式［43］进行过改进，不过改变的仅是经验系数，并且不同的波浪和泥沙条件采用不同的系数值，这间接表明Kamphuis 公式［43］中各个参数的表达形式和指数还有改进余地。Mil-Homens［29］采用Bayram［30］总结的现场和试验资料也改进过Kamphuis 公式［43］，表达式见式（27）。新公式对各参数的指数作了调整，但量纲不和谐问题依旧存在。

式中：Ql为浮质量输沙率，kg/s。

Van Rijn［51］依据量纲分析法也建立了沿岸输沙率公式，见式（28）和（29），其最大的特点是认为公式适用于0.1～100 mm 的泥沙粒径范围，泥沙类型从细沙到卵砾石。Van Rijn 公式［51］与Kamphuis 公式［43］相比，考虑的影响因素相同，表达形式相近，各因素的影响在定性上相同，只是对周期的考虑方式有所不同。Van Rijn公式［51］中波浪周期的影响是通过分析涌浪占比来间接实现的，涌浪占比大则输沙率大。回顾Van Rijn 公式［51］的建立过程，其最大的问题在于率定的数据点并非完全取自于实测点，还包括经率定和验证后的CROSMOR 数模预测点，而该模型关于输沙率的计算本身就是应用的Van Rijn 早期公式（TRANSPOR2004），对于泥沙粒径、岸滩坡度、波浪周期等因素的关系描述已自成逻辑体系，模型计算点据不能等同于实测资料。此外，Van Rijn公式［51］也存在量纲不和谐问题。

式中：Qm为质量输沙率，kg/s；Kswell为涌浪系数，pswell为涌浪出现频率。

关于其他几位学者建立的公式，佩什金—马克西米乌克—阿维林公式［2］将糙率视作引起波能衰减的主要原因，这对于非破碎波底部切应力引起的推移质输沙可能是更适用的，对破碎波紊动耗散引起的输沙而言影响次之。Van Hijum 公式［44］、Chadwick 公式［45］和Van Der Meer 公式［47-49］是针对卵石、砾石滩建立起的沿岸输沙率公式，具有特定的应用场景。Arcilla 公式［46］对于泥沙粒径的影响是以临界启动切应力的方式进行量化，这种方式可能也更多适用于非破碎波底部切应力引起的推移质输沙计算。Van Wellen 公式［50］建立在数学模型BORESED 的敏感性参数分析基础上，与Van Rijn 公式［51］类似，也存在数据库问题。Shaeri 公式［52］的推导过程与Kamphuis公式［43］非常接近，因此最终的表达形式也与Kamphuis公式［43］相近，有些影响因素的指数也是相同的，只不过该公式没有考虑岸滩坡度，同时也存在量纲不和谐问题。

总体而言，量纲分析法能够尽可能多的考虑各种影响因子，通过实测资料敏感性分析来判断沿岸输沙与各种影响因子的定量关系，优势明显。不过，由于该方法属于经验方法的一种类型，公式建立过程往往并不考虑明确的物理机制，可能造成量纲不和谐问题。采用量纲分析法与其他具有明确物理机制的研究方法相结合的模式，则可以扬长避短，既能够较全面地考虑各种因素，又有助于解决量纲问题，如孙林云公式［4］。

3 沿岸流计算方法

沿岸流法常见的计算方法是获取沿岸输沙的横向分布，首先求得破波带内横断面各点上的沿岸流流速及近底波浪轨迹速度等，然后采用适当的波浪或波流共同作用下输沙率公式求得各点的单宽输沙率，通过积分再求得总输沙率［53］，如Bijker公式［54］、Engelund-Hansen公式［55］、Ackers-White公式［56］、Van Rijn公式［57-59］、王尚毅公式［60］、Watanabe 公式［61］和陈超公式［62］等。这类公式往往考虑因素全面，输入参数多，但结构复杂，难以通过积分直接得到表达简洁的总输沙率公式形式，不便于直接使用，在数值模拟应用中具有较好的表现。

上述公式严格来说属于横向分布计算公式，在这些公式当中，王尚毅公式［60］相对而言最具便捷性。王尚毅和周本凡［60］提出了海床稳定性条件和造床波浪计算式，并比照其在河流泥沙运动中提出的输沙模式，建立了包含悬移质和推移质两部分的波流共同作用输沙率公式。该公式计算所需的基本参数为泥沙粒径、岸滩坡度、破波波高、周期和破波角，参数要求与大部分的沿岸输沙率计算公式相近，通过这些基本参数对其他理论或经验参数再推算，最终可求得沿岸输沙率。王尚毅公式［60］形式见式（30）～（34）。

式中：qs为单宽悬移质输沙率，m3/（s·m）；qb为单宽推移质输沙率，m3/（s·m）；u*为水流摩阻流速，m/s；Cδ为床面层上相对体积比计的含沙量；δ为床面层厚度，mm；K为卡门常数；Cb为含沙量参数；v为离海岸线x距离处的沿岸流平均流速，m/s；xb为破波带宽度；I1和I2为积分式。

沿岸流法的另一种计算方法是计算破波带平均含沙量和平均沿岸流流速，通过乘积即可直接建立总输沙率公式，这类成果相对较少。岩垣雄一和椹木公式［63］引用了明渠中Kalinske-Brown的输沙公式，考虑了岸滩坡度、泥沙粒径和周期的影响，该公式应用于日本海岸，泥沙粒径相对较粗（中值粒径1.23～11.4 mm），沿岸输沙一般以推移质为主。卡拉乌谢夫—什瓦尔茨曼［2］基于通过扩散理论得到的垂线含沙量分布推导了输沙率公式，未考虑泥沙粒径、波浪周期和岸滩坡度等其他影响因子。关于明渠水流输沙原理，值得讨论的是，引用该原理计算波浪引起的沿岸输沙时，机理上可能存在一些不适用。破波带的泥沙运动与能量衰减不仅仅取决于波浪作用下的底部切应力和底摩阻，同时还与波浪破碎本身引起的能量耗散有关，并且波浪破碎应该是主要的影响因素，这与明渠水流有很大不同。

一般而言，波浪是沙质海岸破波带泥沙运动的主要动力，波生沿岸流属于波浪破碎产出的次生动力，因而从能量角度沿岸流影响可归为波浪。与能量原理和量纲分析法有所不同的是，除波浪本身外，沿岸流法往往还借鉴破波带外波流共同作用下的输沙率计算方法，在破波带内也考虑沿岸流对海床泥沙的起动和输运，这是该类方法的一大特点。总的来说，采用沿岸流法建立的沿岸输沙率公式主要集中在沿岸输沙横向分布计算，应用相对不便，成果面向数值模拟居多，而直接建立总沿岸输沙率公式的成果较少。

4 常用沿岸输沙率公式检验

以往多位学者对一些沿岸输沙率公式开展过定量检验工作，如孙林云和刘家驹［64］、Sanil Kumar 等［65］、Bayram 等［30］、Mafi 等［41］、Mil-Homens 等［29］、Van Rijn［51］、陈超和张庆河［62］、Shaeri 等［52］。在前文对沿岸输沙率公式主要研究成果回顾的基础上，尽可能汇总前人不同的现场和室内沿岸输沙实测资料，力求以更丰富的数据量，进一步对比分析国内外常用沿岸输沙率公式的预测准确性。常用公式分别为CERC公式［14］、赵今声公式［20］、Kamphuis公式［43］、孙林云公式［4］和Bayram公式［30］。

4.1 资料来源

收集的检验资料共有11处来源，包括现场原型沙、室内原型沙和室内轻质沙共230个点据，数据基本情况见表1。

4.2 检验结果

各常用沿岸输沙率公式的实测资料检验散点图分别见图5～9。为定量分析各公式的预测准确程度，选择均方根偏差Srms计算各公式预测值与实测值的偏差程度，并分别统计预测值与实测值在0.5～2.0倍和0.25～4.00倍关系内的占比。Srms的计算公式见式（35），该参数值越小，则公式预测准确性越高。统计结果见表2。

表2 常用输沙率公式预测结果准确性统计参数Tab.2 Statistical parameters of prediction results for commonly used longshore sediment transport rate formulas

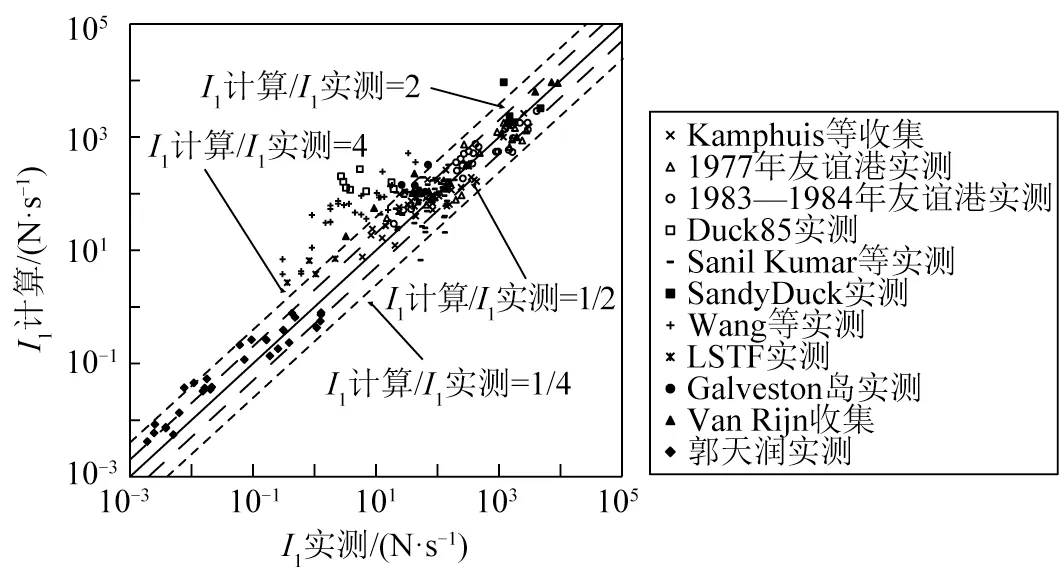
图5 CERC公式检验Fig.5 Evalution of the CERC formula

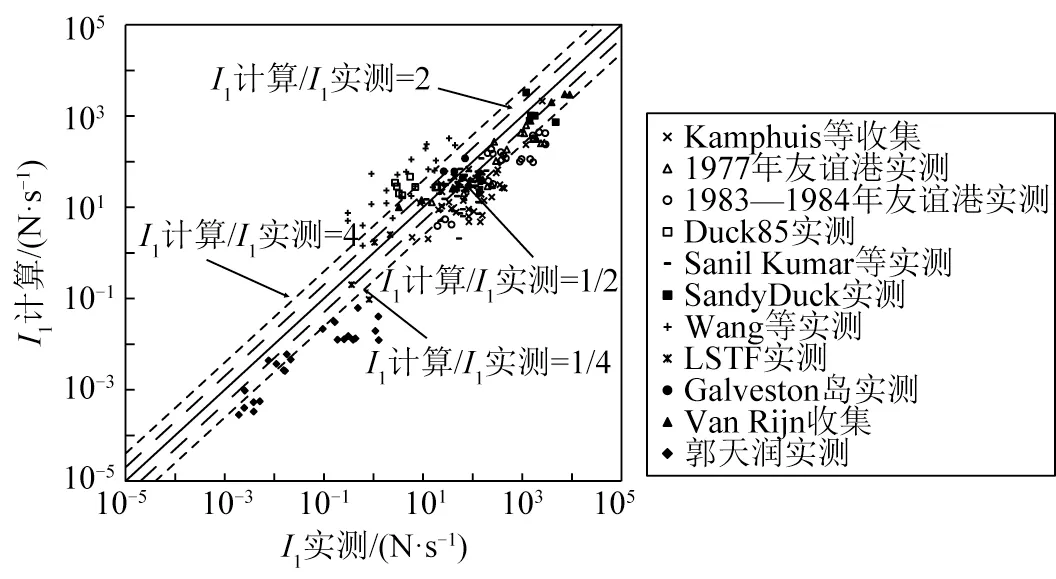
图6 赵今声公式检验Fig.6 Evalution of the Zhao Jinsheng formula

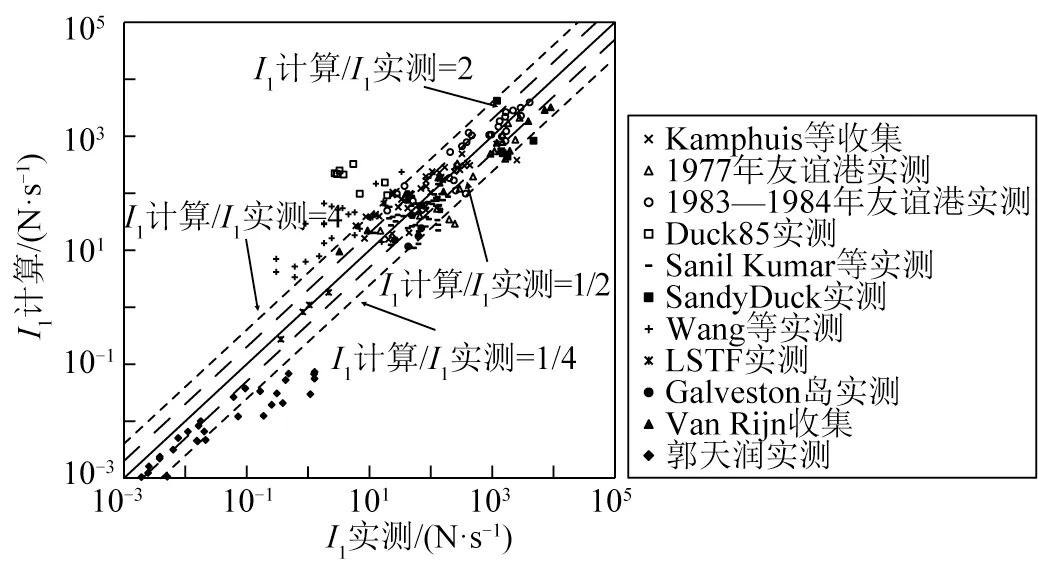
图7 Kamphuis公式检验Fig.7 Evalution of the Kamphuis formula

图8 孙林云公式检验Fig.8 Evalution of the Sun Linyun formula

图9 Bayram公式检验Fig.9 Evalution of the Bayram formula

4.2.1 CERC公式

CERC公式［14］对于现场较大量级输沙率的吻合性相对好一些，但对于中小量级输沙率，尤其是室内原型沙和轻质沙的实测输沙量，该公式总体计算偏大，这与以往Komar 和Inman［12］给出的结果是一致的（图1）。如前文所述，CERC 公式［14］的系数K为恒定值，不能体现泥沙粒径、颗粒容重、岸滩坡度、波浪周期、波陡、破波类型等其他因素的影响，因此对于室内原型沙和轻质沙预测均不适用。统计结果表明，CERC公式［14］的偏差系数Srms为1.33，0.5～2.0倍和0.25～4.00倍关系占比分别为53%和78%。

4.2.2 赵今声公式

赵今声公式［20］考虑了泥沙粒径、波高、周期等多种因素的影响，但其预测结果对于各种量级原型沙与轻质沙资料的吻合程度均较低，公式预测值总体偏小。统计结果表明，该公式的偏差系数Srms为1.73，0.5～2.0倍和0.25～4.00 倍关系的点据分别仅占24%和50%，公式预测偏差较大，这表明公式中各影响因子所反映的基本规律可能欠佳。赵今声公式［20］最大的特点是，沿岸输沙计算值随波陡和粒径发生非单调变化。以泥沙粒径为例，陈超和张庆河［62］在检验赵今声公式时曾对公式中粒径影响进行过分析，表明粒径在大约0.9 mm时具有最大的输沙率，随着粒径减小或增大，输沙率均会减小。在众多沿岸输沙率公式中，该公式所反映的这种变化规律是独特的，结合文中检验结果和一般认知，这种变化规律的合理性欠妥。因此，赵今声公式［20］对各项实测资料的适用性均较低。

4.2.3 Kamphuis公式

Kamphuis 公式［43］的预测结果对于现场原型沙和室内原型沙的资料吻合性相对较好，这与Kamphuis 建立公式时自身检验情况一致（见图4）。不过，Kamphuis公式［43］对于室内轻质沙的预测结果均偏小，这主要是因为该公式并没有考虑泥沙颗粒容重的影响。相比于原型沙，相同粒径的轻质沙容重较小，输沙率相对较大，因而Kamphuis 公式［43］预测偏小。统计结果表明，Kamphuis 公式［43］的偏差系数Srms为1.38，0.5～2.0 倍和0.25～4.00 倍关系占比分别为47%和76%。与CERC 公式［14］相比，Kamphuis 公式［43］的整体偏差水平相近，但其对室内原型沙预测的吻合性较好。总体而言，Kamphuis 公式［43］可适用于原型沙的预测，但不适用于轻质沙的预测。

4.2.4 孙林云公式

孙林云公式［4］考虑的影响因素较全面，其预测结果对于现场原型沙、室内原型沙和室内轻质沙的资料吻合性总体均较好。统计结果表明，孙林云公式［4］的偏差系数Srms为1.00，0.5～2.0倍和0.25～4.00倍关系占比可分别达到62%和87%，公式预测的吻合程度是最高的，表明该公式中各影响因素所反映的基本规律是合理的，公式预测的可靠性较高，具有较广泛的适用性。

值得讨论的是，以上4个公式对于Duck85［67］和Wang等［17］实测资料的预测结果均明显偏大，这很可能是由于这两次资料的输沙率收集不充分。其中，Wang 等［17］在进行现场输沙率收集时，曾在3 处研究区域分别采用捕沙器和挡沙堤拦沙两种方式进行对比，结果表明通过捕沙器获得的输沙率偏小近2～3 倍，而Wang等17］收集的资料绝大多数是基于捕沙器。因此，至少Wang等［17］实测资料存在输沙率严重偏小的问题。

4.2.5 Bayram公式

Bayram 公式［30］考虑的影响因素也较全面，但对各项实测资料的预测结果以明显偏小为主。与前面4个公式不同的是，Bayram 公式［30］对Duck85［67］和Wang 等［17］实测资料的预测准确程度相对好一些，这主要是由于该公式率定时数据源包含了这两组资料，因此公式的预测准确性实际受到了这两组资料的影响，率定参数计算偏小，导致对其他大多数实测资料均预测偏小，适用性较低。统计结果表明，Bayram 公式［30］的偏差系数Srms为1.73，0.5～2.0倍和0.25～4.00倍关系占比仅20%和43%，偏差水平与赵今声公式［20］相近。

综合以上分析，赵今声公式［20］和Bayram公式［30］的预测准确程度最低，对于现场与室内试验、原型沙与轻质沙的适用性均较低。CERC 公式［14］与Kamphuis 公式［43］表现相近，对于现场原型沙的输沙预测相对合理，其中Kamphuis公式［43］对室内原型沙预测的吻合性也较好，但这2个公式均不适用于室内轻质沙预测。孙林云公式［4］的预测结果对现场原型沙、室内原型沙和室内轻质沙各项实测资料的吻合程度最高，公式具有较广泛的适用性。通过对比可见，在众多沿岸输沙率公式当中，孙林云公式［4］具有明显的先进性。

5 讨论与展望

除能量法、量纲分析法和沿岸流法外，一些学者还采用其他方法研究了沿岸输沙率公式。如Manohar［70］将海滩底面上的冲刷率当作输沙率建立了公式。Kraus 等［71］认为总输沙率与沿岸流水体交换有关，基于该理念建立了沿岸输沙率公式。Ribberink 和Al-Salem［72］分别对规则波、不规则波以及不对称波形条件下的输沙率进行了研究，但都是基于非破碎波条件。王玉海［73］采用了高强度推移质输沙过程中固—液混合体运动的新理论模式，建立了计算强浪作用下的推移质输沙率。Tomasicchio 等［74］从类比防波堤块石稳定角度出发，建立了从沙到卵砾石尺度的统一沿岸输沙率公式。Barbaro 等［75］将沿岸输沙与辐射应力建立了关系，从而考虑了波浪谱形态对输沙率的影响。以上这些公式所依据的方法大多并不主流，理论支撑和公式的可靠性还有待时间检验。

纵观数十年的沿岸输沙率公式研究成果，能量法原理凭借其物理意义明确、公式结构简洁等特点，成为业内应用最为普遍的沿岸输沙率计算方法。CERC 公式［14］作为能量法公式中的最早成果，不仅推动了能量法原理的不断发展，也促进了其他多种理论的创新与应用，有力地推进了沿岸输沙率公式这一领域的研究工作，但该公式仅考虑了波能的贡献，考虑因素不全面，公式系数有待完善。在CERC公式成果的基础上，经过半个多世纪众多学者的研究，业界对于系数表达形式、影响因子等方面的探讨不断深入，发展至今逐步形成了以基于量纲分析法的Kamphuis公式［43］和基于能量法的孙林云公式［4］等为主要代表的研究成果，这类代表性公式具有表达形式简洁、考虑因素较全面、物理概念较准确等突出特点，这些特点也正是沿岸输沙率公式理应追求的目标。

在回顾沿岸输沙率公式研究成果的基础上，采用多种实测资料对常用公式的预测准确性进行了定量检验。CERC公式［14］与Kamphuis公式［43］预测现场原型沙相对合理，其中Kamphuis公式［43］还可适用于室内原型沙预测，但这2 个公式均不适用于室内轻质沙预测。赵今声公式［20］和Bayram 公式［30］预测准确程度均较低，对于现场与室内试验、原型沙与轻质沙均不适用。孙林云公式［4］对现场原型沙、室内原型沙和室内轻质沙等各项实测资料的吻合程度最高，适用范围广，符合现场和室内两种尺度下沿岸输沙统一规律，在众多沿岸输沙率公式中具有明显的先进性。

总的来说，沿岸输沙率公式研究成果丰富，通过成果回顾和实测资料检验，展示了各代表性公式的特点和适用性，为未来进一步深化研究奠定了良好基础，不过仍有许多工作有待进一步深化。如在资料收集方面，文中针对国内外常用公式检验的数据源中，可收集到的室内原型沙资料相对较少。此外，轻质沙作为室内模拟河流海岸泥沙运动的一种模型沙，对实现泥沙输移和岸滩冲淤变形相似发挥了重要作用。自20世纪70 年代，以友谊港援建为契机，南京水利科学研究院在国内率先开展了以轻质沙为模型沙的沙质海岸动床泥沙物理模型试验，积累了一批重要成果，采用轻质沙开展波浪沿岸输沙模型试验也写入了中国《水运工程模拟试验技术规范》（JTS/T 231—2021）［76］，但目前国内外对于室内轻质沙沿岸输沙与岸滩演变试验的研究成果总体仍然较少。受限于少有的室内轻质沙试验研究，沙质海岸物理模型的沿岸输沙相似律问题始终得不到很好的解决。因此根据上述讨论，对未来研究工作作出两点展望：

1）未来可进一步收集室内原型沙实测资料，并辅以必要的物理模型试验，深入开展包括规则波和不规则波作用下轻质沙沿岸输沙基本规律研究，充实不同动力泥沙环境的实测资料，进一步扩大沿岸输沙率公式检验的数据量级范围。

2）孙林云公式从能量原理出发，表达形式简洁、考虑因素全面、物理概念准确，符合现场和室内沿岸输沙统一规律，在众多沿岸输沙率公式中具有明显的先进性和广泛的适用性，因此公式改进不作为发展方向。重点推荐孙林云公式作为下阶段推导沿岸输沙模型相似律的依据，相关成果对沿岸输沙物理模型的模型沙选择、创新模型相似理论和提升模拟技术水平具有重要意义。