航空高速湿转子发电机油摩损耗相关因素分析

2023-12-20赵明胤赵博鲁炳林杨鹏刘捷

机床与液压 2023年23期

赵明胤，赵博，鲁炳林，杨鹏，刘捷

(1.山东理工大学电气与电子工程学院，山东淄博 255000；2.山东山博电机集团有限公司，山东淄博 255200)

0 前言

航空起动/发电机作为飞行器发动机起动阶段的动力源和飞行阶段供电系统的核心，具有重要的研究意义。对于长时间处于工作状态的飞行器来说，发电机的运行稳定性至关重要[1-4]。

由于发电机工作在恶劣的航空条件，且高转速运行会使得发电机单位体积的损耗及温升大幅增加，因此，需要设计有效的散热系统来提升发电机的安全性能。高温条件下空气对流散热效果有限，通过直接浸油冷却的散热方式可以在很大程度上解决电机散热问题。同时，冷却油对发电机轴承也起到润滑的作用，增加了轴承的使用寿命，这种用于航空浸油结构的发电机称之为航空高速湿转子发电机。然而，直接油冷的方式会使得气隙内的冷却油与转子外径壁面存在相对运动，因此在转子外径壁面处会产生一种阻碍其旋转的切向应力，从而带来附加流体摩擦损耗的问题。精确计算并通过设计减小这一损耗显得尤为重要。文献[5]针对航空用电液作动器进行结构设计，通过考虑气隙中转子油摩损耗来分析电机性能，为气隙的选择提供了指导。文献[6]针对潜油电机的特殊结构，利用大量实验数据进行分析计算，推导出基于此结构的机械损耗公式。文献[7]通过实验的方法，研究平滑和凹槽结构的小间隙内浸液转子所受阻力矩变化规律，同时通过实验修正了“短粗型”电机的阻力矩计算公式。文献[8-9]采用了计算流体力学的方法，考虑了定子槽、轴向冷却流对风摩损耗的影响，并得出对应计算模型下的剪切应力对比。

综上所述，当前学者对于影响航空高速湿转子发电机转子油摩损耗的相关因素研究较少，且主要根据理想情况进行研究，缺少实际情况的考虑，未有文献利用流体场物理模型对航空高速湿转子发电机转子油摩损耗进行分析与计算。本文作者以一台额定转速为30 000 r/min的航空高速湿转子发电机为例，以航空冷却油为流体介质，建立三维流场简化模型，研究了转子在高速情况下气隙内流场流动机制，利用CFD数值模拟的方法计算了航空高速湿转子发电机转子油摩损耗，并通过解析法进行对比，最后从电机设计角度出发，定量分析了影响航空高速湿转子发电机转子油摩损耗的关键因素，为航空高速湿转子发电机设计及效率优化提供思路。

1 航空高速湿转子发电机油摩损耗分析

1.1 航空高速湿转子发电机物理模型

对于航空高速湿转子发电机来说，系统会将冷却油通过气隙油路送入到发电机内部，使得定子铁心、定子绕组和转子浸在冷却油中，如图1所示。随后通过冷却油循环的方式将热量带走，可以达到良好的冷却效果。

图1 航空高速湿转子发电机结构

发电机处于高速运转状态时，气隙内的冷却油与转子外径壁面存在相对运动，而冷却油存在一定的动力黏度，因此在转子外径壁面处会产生一种阻碍其旋转的切向应力，从而增大了转子的损耗。

针对冷却油介质在气隙中的运动问题，本文作者利用发电机同轴圆柱体流体域模型进行分析，模型示意如图2所示。在此模型下，流体在气隙内的运动过程可以拆解为轴向的泊肃叶流动和径向及切向的泰勒-库特流动，流体的轴向雷诺数Rea可以表示为

图2 定转子间流体等效模型示意

(1)

式中：vin为流体轴向流动的入口速度，m/s；δ为定转子气隙长度，mm；ν为流体的运动黏度系数，m2/s。

因为实际情况的入口轴向流速较小，因此在计算时可不做考虑，且轴向流动并不会从层流向湍流进行过渡，这就使得气隙中的流动问题主要集中在切向的泰勒-库特流上。

发电机的具体计算参数如表1所示。

表1 航空高速湿转子发电机计算参数

基于发电机特殊的工作环境，发电机内部的冷却介质选用散热性能较好RP-3航空煤油。RP-3航空煤油的物理属性如表2所示。

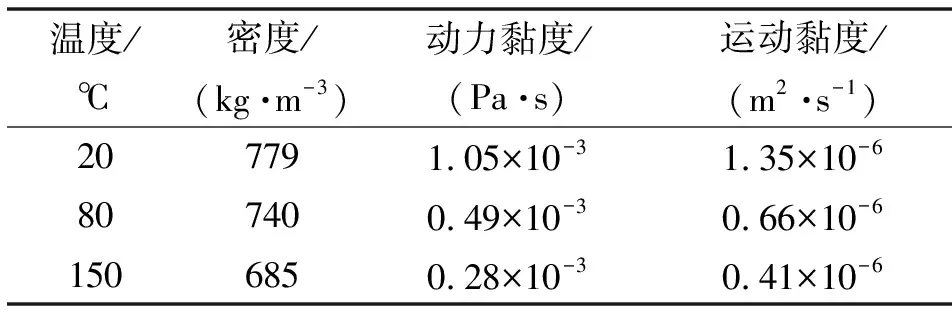
表2 RP-3航空煤油物理属性

1.2 航空高速湿转子发电机数学模型

对于任何具体的流体运动来说，都必须遵守质量守恒定律、动量守恒定律及能量守恒定律这三大基本定律[10]。这三大基本定律对应三个基本方程。

1.2.1 质量守恒方程

质量守恒方程也叫连续性方程，它表示流体密度的变化规律，连续性方程可以表示为

(2)

对于一种稳态、不可压缩的流体来说，其速度的散度处处为0，用速度矢量表示为

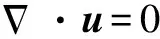
(3)

式中：u表示流体运动的速度矢量，u=u(x,y,z,t)，u、v、w表示速度矢量u在x、y、z三个方向上的速度分量，m/s。

1.2.2 动量守恒方程

动量守恒方程又被称作Navier-Stokes方程，它表征一个流体微元的动量随时间的变化率与作用在该微元上的合力相等，可以表示为

(4)

式中：ρ表示流体的密度，kg/m3；p表示流体单元的压力，Pa；μ表示流体的动力黏度系数，Pa·s；Fx、Fy、Fz表示流体单元上的体积力，N。

1.2.3 能量守恒方程

流体力学的能量守恒考虑了流体密度、温度、内能的变化，具体描述了流体单元中能量的增加率与进入单元体的热流量和体积力及表面力对单元体所做功的和相等。可以表示为

(5)

式中：T表示流体温度，K；cp表示流体的定压比热容，J/(kg·K) ；h表示流体的传热系数，W/(m·K)；ST表示黏性耗散项，J。

1.2.4κ-ωSST模型理论

κ-ωSST模型是由MENTER开发而来的，它是一种剪切压力传输模型[11]，在处理近壁区高度三维流动等问题上发挥了重要作用。κ-ωSST模型对近壁面距离依赖性较强，能够在计算旋转条件时提供自然的湍流黏度，在计算近壁面自由流中具有较高的精度[12]。在湍流条件下可推导的κ方程和ω方程可表示为

(6)

(7)

式中：Γκ和Γω分别表示κ和ω的有效扩散系数；Gκ表示平均速度梯度产生的湍流动能；Gω表示ω的生成项；Yκ和Yω分别表示κ和ω在湍流作用下的耗散项；Sκ和Sω分别表示κ和ω的源项。

对于κ-ωSST有效扩散系数，具体表示为

(8)

式中：σκ和σω分别为κ和ω的普朗克常量；μt为涡流黏度系数，只反映湍流特性。

1.2.5 标准壁面法改进粗糙度模型理论

当考虑粗糙度的概念来分析流体流动问题时，需要依据壁面法则对原始模型进行改进。首先，引入量纲一粗糙高度Ks+和壁面第一层网格的量纲一高度y+，表达如下：

(9)

(10)

其中：Ks表示物理粗糙高度，m；uτ表示流体流动的近壁摩擦速度，m/s；ν为流体的运动黏度系数，m2/s；Δy表示近壁距离，m。

(11)

在κ-ωSST模型中，κ函数不用于壁面计算，因此不受粗糙度改变的影响，而ω函数的计算会受到y+改变的影响。

ω的壁面值ωω具体表达为

(12)

式中：ω+表示量纲一ω函数，可表示为

(13)

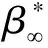
1.3 航空高速湿转子发电机油摩损耗解析计算

在三维旋转流体运动中，气隙内流体的雷诺数Re和转子壁面的阻力矩Te可以表示为

(14)

Te=Cfρν2Lef

(15)

式中：ω表示转子的角速度，rad/s；r表示旋转半径，mm；Cf表示量纲一阻力矩；Lef表示转子轴向长度，mm。

对于切向的泰勒-库特流动来说，流体流动会经历3种流动发展状态，即层流、过渡流和湍流。由于转子处于高速运转状态，其气隙内流体流动已发展为旺盛湍流，因此求解模型应以湍流模型作为参考。高速情况下的气隙内流场不同于经典的泰勒-库特流，湍流流动不能按照层流流动进行解析计算[13]，因此国内外学者大都通过实验进行数据测量。美国学者BILGEN考虑了内圆筒侧面和轴的端部所产生的阻力矩，从而更加精确了只作用在转子壁面处的阻力矩数值大小，最终得出了同轴圆柱体阻力矩系数与气隙宽度和流体雷诺数的函数公式，而且此公式适用于较高雷诺数的场合，具体表达式[14]如下：

(16)

发电机转子油摩损耗计算公式可以表示为

P=0.5Cfπρω3r4Lef

(17)

由此可以推导出转子油摩损耗与转子角速度的关系为

P∝ω2.8

(18)

2 CFD数值模拟分析

2.1 CFD数值模拟计算方法

对于航空高速湿转子发电机转子油摩损耗的研究，除了可以进行实验推导经验公式以外，也可以通过CFD数值模拟计算的方法进行研究。CFD数值模拟计算有效避免了实物制造不便、实验进行难度大和实验周期过长等问题，同时可以进行多目标参数化分析，在验证与改进环节发挥着重要作用。

在进行CFD数值模拟之前，需要对流体场做出以下基本假设：

(1)流体最大流速小于0.3马赫，认为流体处于不可压缩状态[15]；

(2)认为发电机工作状态及流体场处于稳态；

(3)忽略由于温升带来的机械结构变化；

(4)忽略气压、重力等对流体场的影响。

流体流动区域可以分为壁面流动区域和主流区域，而壁面流动区域是湍流产生的主要原因。由于壁面处的速度是理想的，因此在壁面流动区域会存在较大的速度梯度。为保证求解的精度，在CFD分析时需要对壁面流动区域进行精密的网格划分。对于壁面区域的网格划分存在两种方式：壁面函数法和近壁面模型法。其中，当边界层设置较密的网格时，壁面函数法会出现计算无界的错误，因此采用近壁面模型法处理壁面流动区域。

由式(9)可知，uτ是未知的，在计算前需要提供y+的值，之后根据计算结果调整网格高度。对于κ-ωSST模型来说，y+的值接近1为最佳。经过多次计算，得到满足要求的网格类型，如图3所示。

图3 网格剖分

2.2 数值计算与解析计算横向对比

利用表1提供的计算参数，暂不考虑定子槽口因素、定转子偏心度和转子外圆粗糙高度等相关因素的影响，通过仿真分析得到气隙内子午面流场分布如图4所示。可以看出：在转子高速旋转达到稳态之后，气隙内子午面出现泰勒涡，流体已经发展为旺盛湍流状态；最大转速位于转子壁面处，大小为91 m/s。此时轴向压力存在较大梯度，流体单元受惯性力主导，其他速度分量较小，流体切向速度呈波浪状分布。

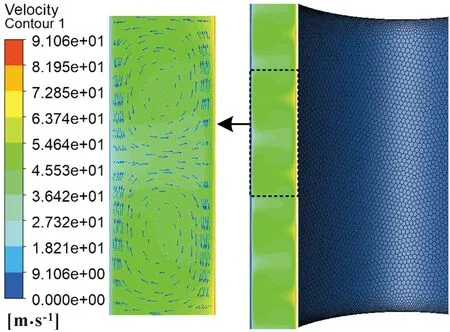
图4 流场分布

CFD计算转子油摩损耗是通过计算流场稳态时转子壁面剪切力得到的。具体表达如下：

(19)

式中：M表示转子壁面的阻力矩，N·m；f表示转子壁面摩擦力，N；τ表示转子壁面剪切力，N；u′ 表示柱坐标系下的流速，m/s；r表示半径，m。

根据数据分析的结果，可得出基于此模型下CFD计算转子油摩损耗与角速度的幂指函数关系，具体表达式为

Ps=5×10-7ω2.833 5

(20)

此结论修正了式(18)中的指数数值，可作为不同转速下初步计算转子油摩损耗的重要参考。CFD数值计算与解析法计算结果横向对比如图5所示。

图5 数值计算与解析计算横向对比

可以看出：两种方法计算得出的转子油摩损耗数值大小接近，计算结果平均相差为3%。随着转速的升高，两种方法计算偏差也相对增大。这是因为公式并未在超高雷诺数条件下进行拟合推导，因此随着转速增大误差也相对增大，需要进行超高雷诺数实验修正。此外，图5还显示了基于CFD计算的拟合结果，与CFD实际计算结果基本吻合。

3 转子油摩损耗影响因素研究

由于发电机实际工作情况并不是理想的，解析法计算转子油摩损耗会存在一定局限性。因此，需要在理想的数值计算基础上，考虑定转子气隙长度、槽口因素、工作温度、转子外圆粗糙高度、定转子偏心度等对转子油摩损耗的影响。以下相关因素研究除参变量外均利用表1的参数进行计算，在不同转速下进行单一变量研究。

3.1 定转子气隙长度对转子油摩损耗的影响

定转子气隙长度不仅决定着发电机的电磁性能，同时也作为影响转子油摩损耗的重要因素之一。不同转速下定转子气隙长度的变化对转子油摩损耗的影响如图6所示。

图6 不同定转子气隙长度对应的转子油摩损耗

可以看出：转子油摩损耗与定转子气隙长度呈正相关，且变化幅度较小。由于定转子气隙长度决定着重要的电磁性能，因此通过减小定转子气隙长度来减小转子油摩损耗的效果不显著，定转子气隙长度的取值应优先满足磁路计算的需要。

3.2 定子槽口尺寸对转子油摩损耗的影响

为使气隙内流体分布更接近于发电机运转真实情况下的分布，需要考虑定子侧槽口对转子油摩损耗的影响。对应流体域模型如图7所示。

图7 考虑槽口大小的流体域计算模型

在图7中，w和h分别表示定子槽口宽度和高度。由发电机电磁设计得出的w和h的值都为2 mm，则考虑槽口因素前后对应的转子油摩损耗如图8所示。

图8 考虑槽口因素前后对应的转子油摩损耗

可以看出：考虑槽口因素时转子油摩损耗明显增加，在额定转速30 000 r/min时转子油摩损耗增加27%，且转速越大，槽口因素对转子油摩损耗的影响越大。此外，由于槽口因素带来的附加油摩损耗问题，需要针对槽口宽度和槽口高度进行分析。在额定转速下改变定子槽口宽度和槽口高度后对应的转子油摩损耗如表3所示。

可以看出，在槽口高度一定时，转子油摩损耗随着槽口宽度的增大而增大。这是因为增大槽口宽度会使得凹槽处流量增大，可等效为增大了定转子气隙长度，进而增大转子油摩损耗。在槽口宽度一定时，改变槽口高度后转子油摩损耗无明显变化规律，且整体变化幅度较小。这是因为高速旋转状态下凹槽内部远离气隙，形成的稳态流动难以改变。因此在设计时，需要将槽口进行绝缘封闭，并使得流道外侧壁面尽可能光滑。如果因嵌线工艺难度无法进行槽口封闭时，设计中应尽可能减小定子槽宽的大小。

3.3 工作温度对转子油摩损耗的影响

发电机工作时会伴随着较大的温升，不同的工作温度会影响流体介质的密度和动力黏度等物理属性，从而对转子油摩损耗产生影响。航空煤油工作温度对转子油摩损耗的影响如图9所示。图9显示了同种流体介质在不同工作温度下对应的转子油摩损耗，随着温度升高，转子油摩损耗呈下降趋势；且转速越高，温度对转子油摩损耗的影响也就越大，但不同温度下转子油摩损耗随转速变化的趋势一致。因此，在选择冷却介质时，要综合考虑冷却介质在不同温度下的比热容和运动黏度，并根据具体工作温度范围确定冷却介质。

3.4 转子外圆粗糙高度对转子油摩损耗的影响

由于转子壁面并不是绝对光滑的，因此计算转子油摩损耗需要引入转子外圆粗糙高度的概念进行计算。转子外圆粗糙高度对转子油摩损耗的影响如图10所示。

可以看出：转子外圆粗糙高度对转子油摩损耗影响较大，在转子外圆粗糙度系数一定时，不同转速下转子油摩损耗随着转子外圆粗糙高度的增大而增大。在额定转速下，当粗糙高度达到5 μm时，对应的转子油摩损耗相对于光滑壁面增加了31.1%，因此在转子加工工艺方面要严格把控，可以通过车削、磨削的精加工方式减少转子外圆粗糙高度，一般精度可控制在1 μm左右；对于运行于较高转速的转子来说，可以通过高精度车床用精细修研的金刚石进行车削，加工后的粗糙高度可以控制在0.01～0.04 μm，可大大减小转子油摩损耗。

3.5 定转子偏心度对转子油摩损耗的影响

由于制造工艺和装配工艺会存在误差，且发电机在工作过程会受到机械应力与热膨胀等因素的影响，导致转子的旋转中心与定子中心有所偏差[16]，从而改变转子油摩损耗的数值。为方便研究此种偏差对转子油摩损耗的影响，定义偏心度e为定转子偏心量。定义的偏心度可以满足定子偏心和转子偏心两类偏心情况，因此使用同种模型表示即可。

偏心度计算模型如图11所示。