新型变指数趋近律的PMSM滑模控制

2023-12-20李璐谭草张玉学郭春霖孙兆岳王子喆

机床与液压 2023年23期

李璐，谭草，2，张玉学，郭春霖，孙兆岳，王子喆

(1.山东理工大学交通与车辆工程学院，山东淄博 255049；2.山东中保康医疗器具有限公司，山东淄博 256407)

0 前言

近年来，电力电子技术快速发展。永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有体积小、质量轻、功率密度高、启动转矩大等优点[1-3]，已在汽车、航天、机器人等领域得到了广泛的应用。

滑模控制作为一种变结构非线性的控制方法，相比于传统的PI控制具有响应快速和强鲁棒性的优点，并且对内部参数和外部扰动不敏感，广泛应用于PMSM调速系统。但滑模控制的一个主要缺点是系统状态变量在滑模面附近做滑模运动时，会发生抖振现象[4-6]。解决抖振问题已成为滑模控制的热点研究问题。

文献[7]提出一种基于新型滑模趋近律的鲁棒控制策略，并在位置环引入了积分-非奇异终端滑模控制器，仿真验证了该控制器可有效克服系统结构参数的变化，并提高了响应能力。文献[8]提出一种新型分数阶趋近律，将幂次趋近律与分数阶微积分相结合，应用分段型指数函数代替趋近律中的符号函数；仿真结果表明：该方法能有效解决传统滑模控制中存在的问题，具有抖振小、控制精度高等优点。文献[9]提出一种基于高阶滑模观测器与新型滑模速度控制器相结合的PMSM无传感器矢量控制方法，用高阶滑模观测器代替传统滑模观测器，用新型滑模转速控制器代替传统比例积分转速控制器，仿真结果表明：新型双滑模控制系统转速的超调量与抖振更小。文献[10]采用边界层可变的正弦型饱和函数替代传统符号函数，提出一种用于PMSM无传感器控制的软开关滑模观测器，实验结果表明，新型滑模控制器有效消除了估计结果的抖振。

本文作者在传统幂次趋近律的基础上引入一个变指数项，加快了系统的收敛速度，并且将滑模趋近律的符号函数替换成正弦饱和函数，抑制了系统的抖振问题；针对外部扰动对滑模控制系统的影响，设计非奇异快速终端滑模扰动观测器，避免较大的滑模增益，解决系统的抖振问题。仿真实验结果表明：结合扰动观测器的新型变指数趋近律滑模控制系统具有响应速度快、抖振小、抗干扰能力强的特点。

1 PMSM数学建模

永磁同步电机是一个非线性、多变量、强耦合的复杂系统。忽略永磁同步电机铁芯饱和、磁滞损耗、涡流损耗等影响，对永磁同步电机三相坐标系进行数学建模，永磁同步电机同步旋转坐标系下的数学模型[11]为

(1)

(2)

(3)

对于表贴式PMSM，由于转子磁路对称，有Ld=Lq，故式(3)可以表示为

Te=3/2npφmiq

(4)

电机机械运动方程：

(5)

一般在电机调速系统中，把外界负载TL看作外部扰动d(t)，则式(5)可表示为

(6)

其中：Rs为定子电阻；ωe为转子电角速度；id、iq分别为定子d、q轴电流；ud、uq分别为定子d、q轴电压；Ld、Lq分别为定子d、q轴电感；np为电机极对数；φm为永磁体磁链；w为微分算子；Te、TL分别为电磁转矩和负载转矩；J为转动惯量；B为黏滞摩擦系数；d(t)为外部扰动。

2 控制器的设计及稳定性证明

2.1 改进变指数趋近律滑模控制器

首先定义电机的参考转速为ωref，实际转速为ωm，可得出速度误差和其变化率：

(7)

非奇异终端滑模(Non-singular Terminal Sliding Mode，NTSM)解决了终端滑模奇异性问题，但在系统误差到达滑模面后，其收敛速度表现的要比线性函数构成的滑模面慢。因此，构建非奇异快速终端滑模控制器(Non-singular Fast Terminal Sliding Mode-Controller，NFTSMC)的表达式[12]为

(8)

其中：S(x)是滑模面；x是系统状态变量；θ>0；p、q均为大于0的奇数，且q1。

令S=0，得到速度误差变化率为

(9)

由式(9)可知，系统误差做趋近滑模面的运动时，误差收敛速度取决于指数项，当系统误差接近平衡点时，误差收敛速度主要取决于线性项，保证了全局的收敛速度。

基于传统幂次趋近律的基础建立了快速幂次趋近律，这种新型的趋近律保持了传统幂次趋近律的优点，又进一步加速了全局收敛速度，抑制了系统抖振。现给出其具体的形式，如下所示：

(10)

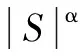
为进一步抑制系统的抖振问题，继续对上述趋近律进行改进，采用一种正弦饱和函数代替符号函数。饱和函数法又称边界层法，利用边界层原理使系统变成连续系统，新型正弦饱和函数的表达式[13]为

(11)

其中：Δ为边界层的厚度，λ=π/2Δ。这样，在饱和层外采用开关切换控制，饱和层内采用线性控制，既保证了收敛速度，又减小了高频切换产生的抖振，保证电机在中低速场合的跟踪性能。

则结合式(6)(8)(10)，新型非奇异快速终端滑模控制律如下：

(12)

2.2 速度控制器稳定性证明

利用Lyapuov稳定性条件加以说明。现定义一个存在一阶偏导数的Lyapuov函数V(x)，如下：

V(x)=1/2S2

(13)

求导得到：

(14)

由式(8)可知：

(15)

上文已推出iq表达式：

(16)

则有：

(17)

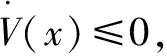
3 扰动观测器的设计及稳定性证明

针对滑模变结构控制在负载扰动时动态性能不佳的问题，设计非奇异快速终端滑模转矩观测器，实时观测负载转矩的变化，并将观测得到的扰动量前馈至电流给定，克服了负载扰动对系统控制性能的影响。

在一个控制周期内，负载转矩变化较慢[14]，一阶导数可看成0，有

(18)

即

(19)

以电机机械角速度ωm和负载扰动量d(t)构建状态方程[12]：

(20)

将机械角速度和系统负载扰动作为观测对象，构建非奇异快速终端滑模观测器方程为

(21)

其中：g为观测器增益；f(eω)为观测的滑模控制率。两次相减得出误差方程为

(22)

其中：ed为扰动观测误差；eω为速度观测误差。

同样选取非奇异快速终端滑模作为扰动观测器滑模面：

(23)

结合上文的新型趋近律，得到扰动观测器的趋近律为

C|Sω|αsat(Sω)+ε|eω|βSω-B/Jeω

(24)

由式(23)(25)可得

(25)

则有

ε|eω|βSω-B/Jeω)≤0

(26)

由式(26)可知，扰动观测器符合李雅普诺夫第二稳定性理论。图1为文中NFTSMC矢量控制策略系统控制框图。

图1 系统控制框图

4 结果及分析

搭建的基于RTU-BOX的调速系统实验平台实物如图2所示，实验平台包括直流电源、三相全桥逆变器、RTU-BOX控制器、实验电机、负载电机、转速转矩传感器。

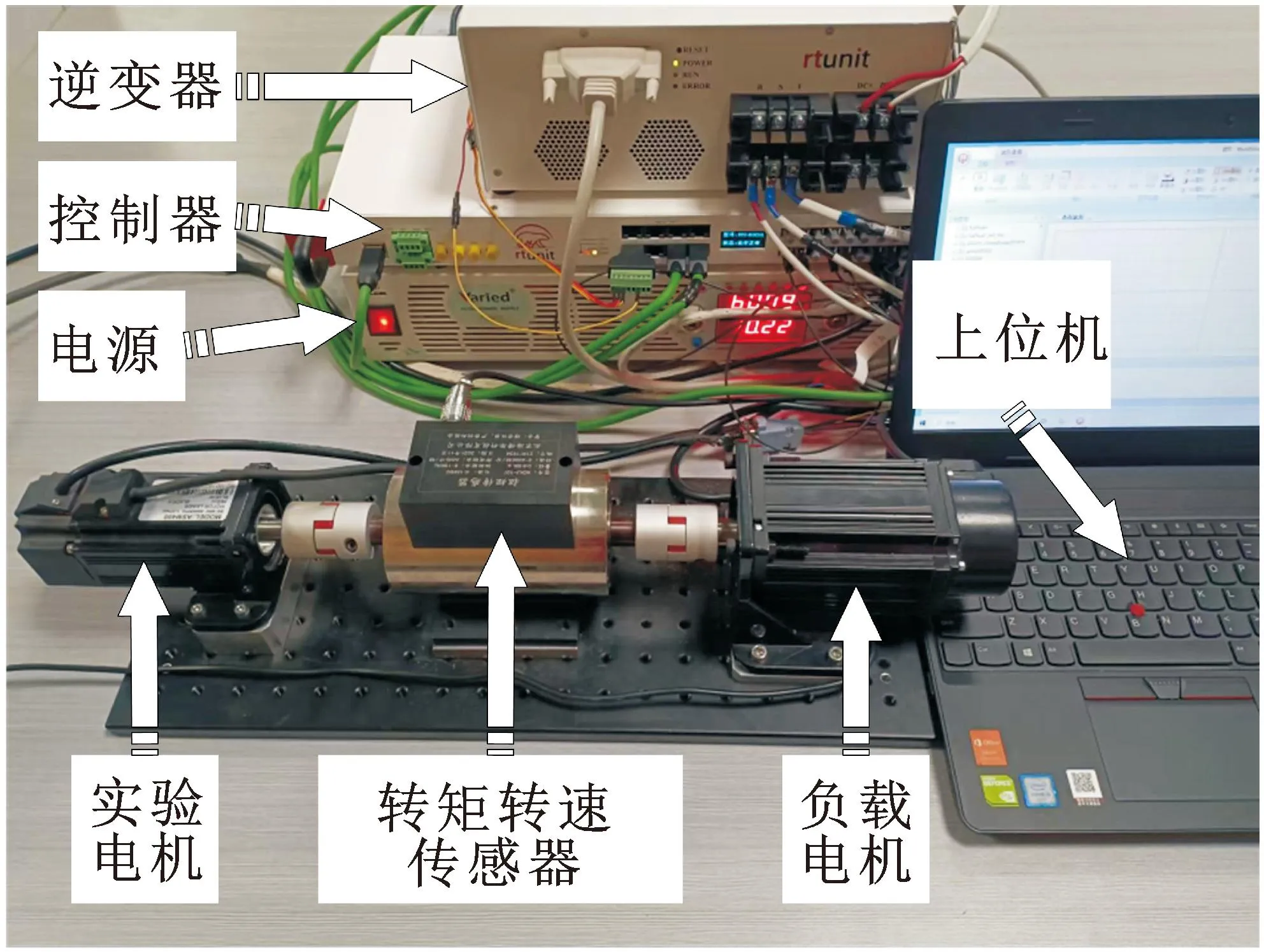
图2 永磁同步电机实验平台

为验证引入负载扰动观测器的基于新型变指数趋近律的NFTSMC转速控制策略控制效果，将MATLAB/Simulink调速系统NFTSMC矢量控制仿真模型嵌入控制器，在保证电机参数相同且采样时间以及仿真条件均保持一致的条件下对基于饱和函数的变指数趋近律的非奇异快速终端滑模速度控制器进行仿真，同时与基于符号函数的变指数趋近律的非奇异终端滑模速度控制器进行性能对比。表1为电机参数。

表1 永磁同步电机的主要参数

4.1 启动工况性能实验

图3为基于不同滑模控制策略控制下的电机启动转速实验波形，电机给定参考转速为600 r/min。其中NTSMC-sgn为基于符号函数的变指数趋近律非奇异终端滑模控制，NFTSMC-sat为基于饱和函数的变指数趋近律非奇异快速终端滑模控制，下文NFTSMC-sat+DOB为结合扰动观测器的基于饱和函数的变指数趋近律非奇异快速终端滑模控制。

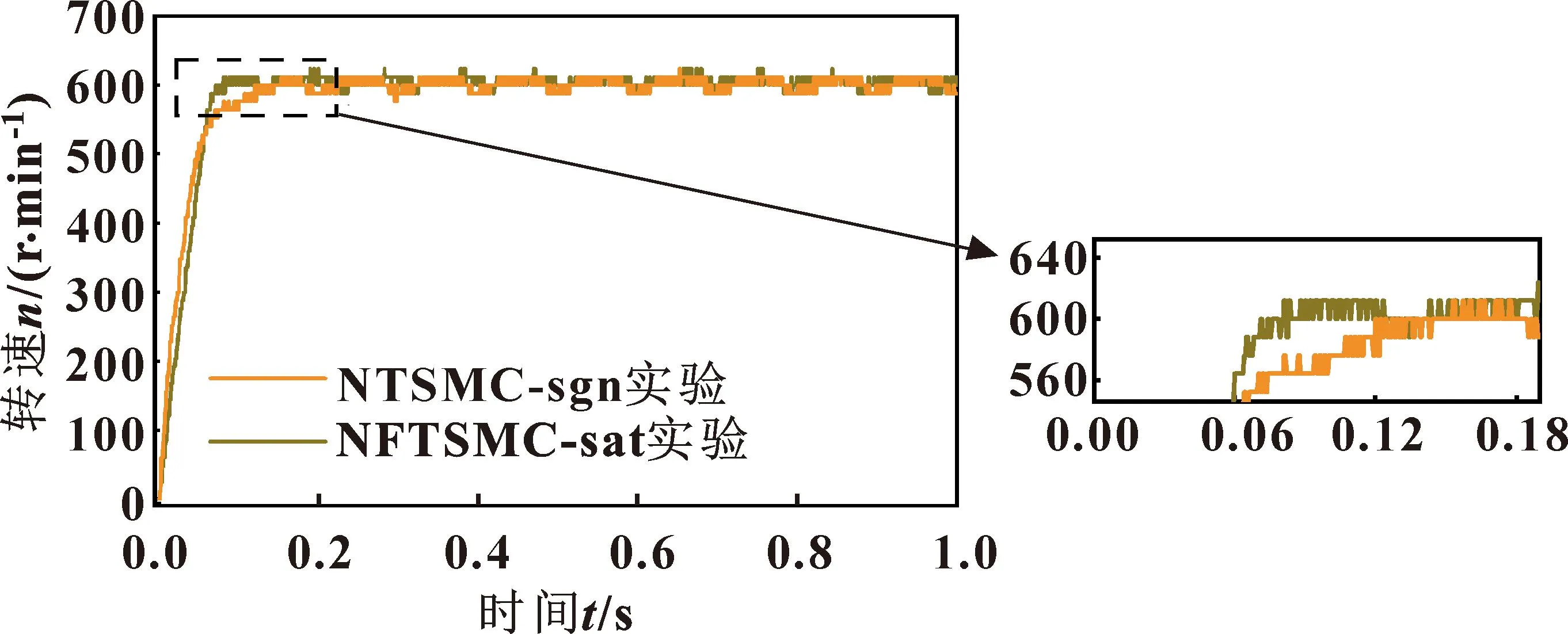
图3 启动工况永磁同步电机转速

由图3可知：基于符号函数的变指数趋近律非奇异终端滑模控制的电机在0.118 s达到参考转速，而所设计的基于饱和函数的变指数趋近律非奇异快速终端滑模控制的电机在0.071 s就达到参考转速，并且达到稳定前无超调。实验证明了所设计控制器的合理性。

4.2 变负载工况性能仿真

启动阶段给定电机负载转矩0 N·m，在0.2 s时突增负载，变成4 N·m，图4为不同控制策略下电机转速响应曲线。

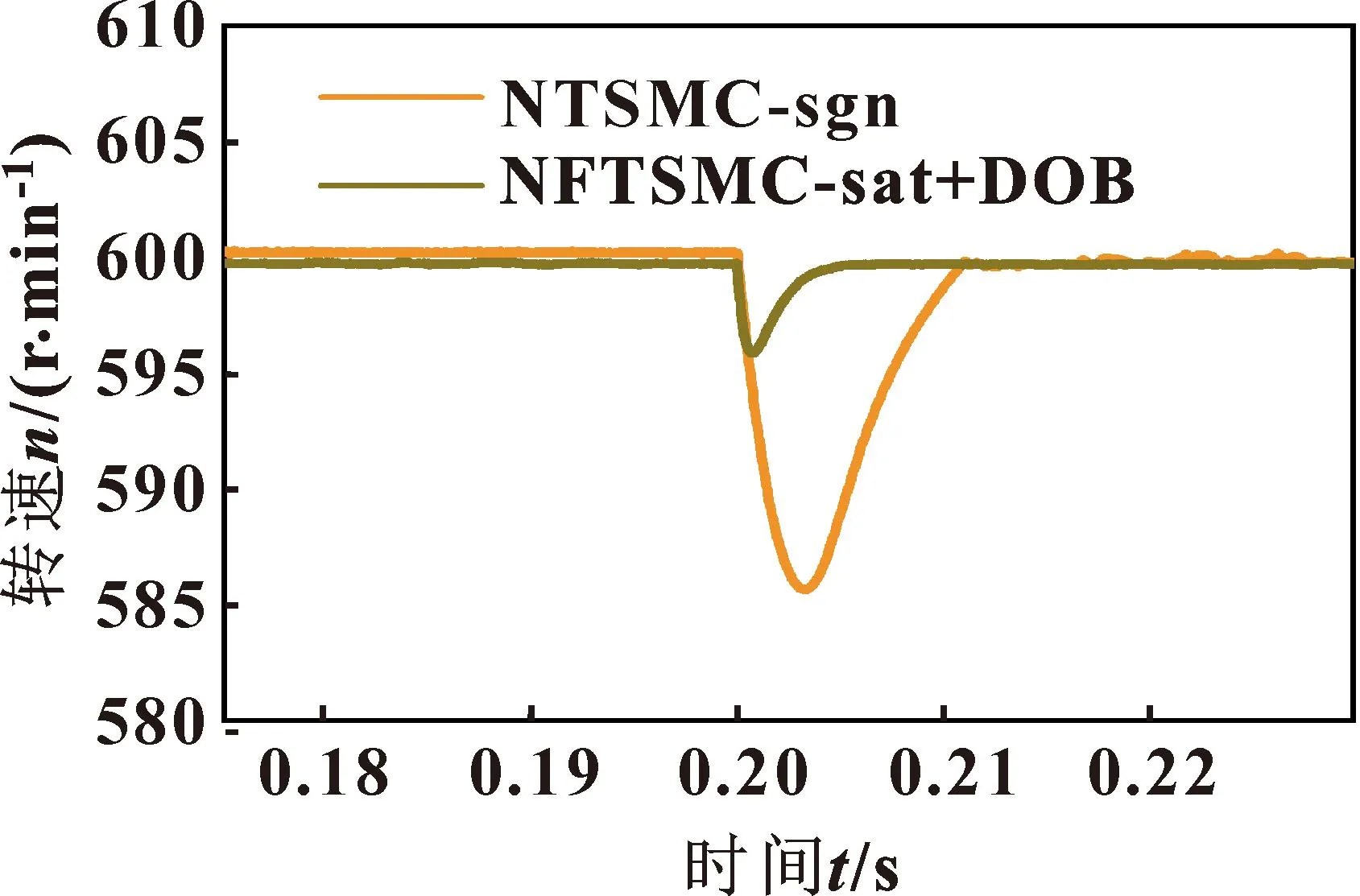
图4 变负载工况永磁同步电机转速

由图4可知：基于符号函数的变指数趋近律非奇异终端滑模控制的电机转速下降到585.6 r/min，且稳定时间较长，转速稳定过程中抖振较大；结合扰动观测器的基于饱和函数的变指数趋近律非奇异快速终端滑模控制的电机转速下降到596.1 r/min，且可以很快稳定到参考转速，稳定后转速波动小。因此，采用基于饱和函数的新型变指数趋近律的滑模控制结合扰动观测器可以有效抵抗外界负载干扰，恢复时间短，且有效降低抖振。

由图5可知：在0.2 s突加4 N·m负载，两种滑模控制下的电机皆很快达到参考转矩，但基于符号函数的变指数趋近律非奇异终端滑模控制的电机转矩达到稳定前超调量比较大；采用引入负载扰动观测器的基于饱和函数的变指数趋近律非奇异快速终端滑模控制的电机转矩在0.206 s就达到了稳定，并且仅略有超调，且稳定阶段波形毛刺少，抖振小，电机转矩平稳。

图5 变负载工况永磁同步电机转矩

4.3 变转速工况性能仿真

在0.2 s时将参考转速600 r/min突变为900 r/min，整个过程带载运行，负载为2 N·m，基于两种控制类型的变转速工况电机电磁转矩响应曲线如图6所示。可知：采用基于符号函数的变指数趋近律非奇异终端滑模控制的电机，0.2 s转速突变时，在0.208 s恢复稳定，但稳定运行时抖振较大；采用基于饱和函数的变指数趋近律非奇异快速终端滑模控制的电机电磁转矩在0.205 s恢复稳定，恢复速度快，达到稳定时超调较小，稳定运行时转矩波形较为平稳。