基于SSA-PSO-BP神经网络航空壁板装夹变形预测研究

刘红军，邵泓斌

(沈阳航空航天大学机电工程学院，辽宁沈阳 110136)

0 前言

薄壁件因其质量轻、强度高、承载能力强等优点，如今被广泛应用于航空领域，如整体隔框、整体翼肋等[1]。现对机翼进行盲制孔，因受其工装夹具的影响，机翼中的壁板在安装夹具后会相较于未安装夹具前发生轻微变形，若不考虑则会导致最终盲制孔位置与期望的位置发生偏差，从而影响制孔精度。

受加工效率及加工条件的影响，对壁板变形量的测量无法通过众多的激光测距传感器实现。为提高盲制孔的加工精度，有必要建立一种航空壁板的变形预测算法，对航空壁板安装夹具后的变形进行准确的预测。

赵欣等人[2]运用Abaqus软件模拟了叶片加工过程的变形量，并通过正交试验获取切削参数、刀具倾角等数据来观察叶片变形的影响规律，最后通过线性回归的分析方法拟合出预测模型。王骏腾等[3]考虑到薄壁件的结构复杂，且时变加工工况造成的残余应力难以获取，分析了几种典型装夹方式的感知过程，提出了一种感知预测模型，实验结果表明：预测值与实测值相比，误差为13%，具有较好的一致性。CHENG等[4]采用有限元仿真的方法建立了三维钛合金薄壁铣削模型，并分析了其变形规律。于金、王胤棋[5]为解决Abaqus软件仿真运算时间较长的问题，采用Python语言编写脚本对Abaqus软件进行了二次开发，仿真预测时间缩短，可较好地预测大型曲面薄壁件加工时的变形情况。王庆霞等[6]运用AdvantEdge软件建立三维铣削加工的有限元模型，根据仿真得到的结果确立了进给速度、切削力和工件切削时加工变形之间的多项式数值模型，从而实现对加工过程中变形的实时预测。屈力刚等[7]首先根据薄壁件的加工路径构建了UKF预测模型，其次把在机测量系统的检测数据作为已知噪声输入到UKF算法中进行预测模型的训练，最后使用MATLAB预测出零件的变形量，根据试验对比，预测变形量精度从45.7%提高至74.2%。HUANG等[8]为了提升预测零件变形的计算效率，首次使用了结构分析、特殊网格生成和结构静态刚度修正结合的方法，提出一种新的有限元模型，最后计算零件随时间和位置变化的变形量，预测壁厚误差。秦国华等[9]针对航空薄壁零件，采用了神经网络的方法对装夹布局进行了预测、控制与优化。韩军等人[10]将Abaqus有限元仿真与BP神经网络结合的方法应用到齿圈装夹变形预测中，得到的预测结果与实际值相比较误差在0.05%之内。陈永当等[11]首先运用Python对Abaqus进行二次开发，对建模周期进行了缩短和简化，其次通过对BP神经网络的训练，对最大铆接变形量进行了预测，性能较好。

上述学者对模型的变形预测大多使用Abaqus有限元软件进行分析，缺点是预测时间较长，效率低。韩军等人[10]通过Abaqus与BP神经网络结合的方法，先通过Abaqus仿真模型获取训练样本的数据，再使用BP神经网络的方法进行变形预测，大大减少了运算时间，提高了预测的效率，但BP神经网络并没有对初始权值和阈值进行优化，容易陷入局部最优解，造成预测值的精准度降低。李乐等人[12]使用粒子群算法对BP神经网络初始权值与阈值进行了初次优化，预测精度有了较大的提升。

本文作者将根据航空壁板实际的装夹情况，采用Abaqus有限元仿真与神经网络相结合的方法，首先对航空壁板进行有限元分析，从而获取神经网络所需要的训练以及预测数据；其次提出一种改进的神经网络预测算法，即SSA-PSO-BP预测算法，快速且准确地预测航空壁板装夹后的变形量。

1 航空壁板装夹变形有限元分析

对现场安装夹具后3个激光测距传感器的测距值进行记录，作为神经网络的输入值输入到Abaqus软件中，对壁板进行仿真变形预测，将得到的8个预测值作为神经网络的输出值。总共得出50组数据集作为神经网络的训练以及预测。

此次使用Abaqus2020有限元软件建立壁板装夹变形的仿真分析，研究壁板制孔处x方向的位移，主要涉及几何模型建立、材料属性赋予、边界条件及接触定义、网格划分共4部分内容。

(1)几何模型设计与建立。对航空壁板实际模型进行适当的简化，并在SolidWorks软件中进行等比例建模，最终导入Abaqus软件中进行有限元分析。

(2)材料属性赋予。航空壁板的材料为Ti-6Al-4V，其中弹性模量E=110 GPa，密度ρ=4 510 kg/m3，泊松比μ=0.34。因航空壁板在实际装夹过程中的塑性屈服并不明显，此处采用Johnson-Cook模型[13]来描述Ti-6Al-4V钛合金的本构关系，表达式如式(1)所示：

(1)

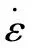
(3)边界条件及接触定义。根据现场实际装夹情况，壁板的上下两段与飞机翼框接触且固定约束，仅允许在x轴与y轴方向上移动。

(4)网格划分。为壁板划分网格时，考虑到其形状复杂且不规则，将其合理地划分为四面体结构网格，选择常用于接触分析的三维应力线性单元，单元类型为C3D10。

仿真后的位移变化云图如图1所示，最大变形量约为2.776 mm。以同样的方法将测得的不同激光传感器数值进行模拟仿真，总共得到50组数据作为神经网络模型的训练样本和预测样本。50组数据如表1所示。

2 SSA-PSO-BP神经网络模型

2.1 BP神经网络

人工神经网络(Artificial Neural Networks，ANN)是1980年以来人工智能领域的重点研究内容，主要用于处理多节点和多输出点的网络结构[14]。BP神经网络属于人工神经网络的一种，属于多层前馈神经网络，其拓补结构主要由输入层、隐含层、输出层组成。

BP神经网络模型结构如图2所示。

图2 BP神经网络结构

目前，BP神经网络已经足够成熟，可以解决大部分的预测问题，但是在使用过程中也逐渐发现其有一定的缺陷：即每次赋予的权值与阈值都是随机的，造成整体神经网络的收敛速度过慢，并且容易陷入局部最优解。

因此本文作者基于传统的BP神经网络，在其原有的基础上先进行一次PSO粒子群优化算法的优化，再进行一次SSA麻雀搜索算法的优化。其目的是为了对BP神经网络的初始权值与阈值进行两次寻优，从而得到改进的BP神经网络，即SSA-PSO-BP神经网络算法，其流程如图3所示。

图3 SSA-PSO-BP神经网络算法流程

2.2 SSA原理

麻雀搜索算法(Sparrow Search Algorithm，SSA)是由薛建凯[15]通过模拟麻雀在自然界的生存过程提出的一种群体优化算法，相较于之前的蝙蝠算法、灰狼优化算法、鲸鱼优化算法等，SSA具有精度更高、收敛速度更快、稳定性更强的优点，并且具有较好的全局寻优能力。

为了更好地生存，麻雀种群通常分为两种类型：发现者和加入者，发现者负责寻找食物，为整个种群提供觅食的方向，其生存能力较强，加入者通过发现者来获取食物，属于弱势个体。发现者与加入者的身份是可以动态变化的，只要能找到食物，每只麻雀都可以成为发现者，但是发现者与加入者占整个种群的比例是不变的，即一只麻雀成为发现者必有另一只麻雀成为加入者。此外，当麻雀意识到危险时，为了保证安全，群体边缘的麻雀会迅速向安全区域移动，不断更新自己的位置。

(1)发现者的位置更新如式(2)所示：

(2)

式中：t为当前的迭代次数，j=1，2，3，…，d；M表示最大的迭代次数；Xi，j表示第i个麻雀在第j维中的位置信息；α是(0，1)内的随机数；R2表示预警值，Ts表示安全值，其中R2∈[0，1]，Ts∈[0.5，1]；Q为服从正态分布的随机数；L代表一个大小为1×d维的矩阵，且矩阵中的各个元素都为1。

当R2

(2)加入者的位置更新如式(3)所示：

(3)

式中：Xp表示当前种群内的最优位置；Xworst表示当前种群内的最差位置；A表示一个大小为1×d维的矩阵，矩阵中的每个元素被随机赋值为1或-1，且满足A+=AT(AAT)-1。

当i>n/2时，表示种群当中的第i个加入者没有找到食物，适应度值较低，需要前往其他区域寻找食物，以获取更多的食物补充能量。

(3)在进行种群模型构建的过程中，假定种群中有10%～20%的麻雀会提前预知到风险，在向种群发出预警信号后麻雀会迅速做出反捕食行为，其位置更新公式如式(4)所示：

(4)

式中：Xbest是当前种群内的最优位置；β表示系统步长控制参数，其数值满足均值为0、方差为1，并且服从正态分布；K为[-1，1]内的随机数；fi为当前第i个麻雀的适应度值；fg表示当前全局最佳的适应度值；fw表示当前全局最差的适应度值；ε表示最小的常数，作用是为了避免分母为零的情况出现。

当fi>fg时，表示此时麻雀处于边缘位置，极易被捕食者发现并受到攻击；当fi=fg时，表示此时处于种群中心的麻雀意识到了危险，需要立即更新自身的位置向危险区域的麻雀靠拢。

3 神经网络实例应用

3.1 神经网络参数设定

根据算法流程图可知，对BP神经网络权值与阈值进行PSO算法的初次优化，其中PSO算法的具体参数设置为迭代次数为20，种群规模为10，学习因子c1=c2=1.494 45；其次采用迭代速度快、全局寻优能力强的SSA对权值与阈值进行二次寻优，SSA的参数为迭代次数为20，种群规模为10，发现者和加入者各占种群数目的20%，预警值R2=0.8。

根据上述参数设定，选取有限元仿真数据中45组数据作为SSA-PSO-BP神经网络的训练数据集对神经网络进行训练，剩余5组数据作为神经网络的预测数据集，验证神经网络是否符合要求。

3.2 三种神经网络预测值对比

为验证此次建立的SSA-PSO-BP网络与BP神经网络以及PSO-BP两种神经网络的不同之处，用训练集对BP网络、PSO-BP网络以及SSA-PSO-BP神经网络进行训练后，分别用于对航空壁板变形进行预测。期望值与各个神经网络的预测值的对比如图4所示，各个神经网络的预测误差如图5所示。

图4 预测值与期望值对比

图5 误差对比

根据图4与图5可以看出：除4号样本SSA-PSO-BP神经网络的预测值误差较大，其他4组测试样本的SSA-PSO-BP预测值较BP与PSO-BP两种神经网络，其预测的准确性明显优于后两者，与期望值的拟合效果更佳。

图6为两种神经网络的适应度进化曲线，与PSO-BP神经网络相比，SSA-PSO-BP神经网络在相同20次迭代次数下适应度趋于平稳的速率更快，经过7次迭代便达到了适应度的全局最优值，并且适应度较PSO-BP神经网络也有了明显的降低。因此，文中所提出的SSA-PSO-BP优化算法对BP神经网络的收敛速度及预测精度提升较大。

图6 适应度曲线对比

为评价各神经网络模型的性能，采用均方根误差(RMSE)以及平均绝对百分误差(MAPE)对预测结果进行精度评定。RMSE可以比较预测值与真实值之间的偏差，MAPE可以衡量一个模型预测结果的准确性。相应的计算公式如式(5)(6)所示：

(5)

(6)

对预测结果进行精度评定，结果如表2所示。

表2 模型准确度对比

由表2可知：BP神经网络的均方根误差是5.32 mm，平均绝对百分误差为0.79%；PSO-BP神经网络的均方根误差是0.61 mm，平均绝对百分误差为0.34%，比BP神经网络有了明显的降低；而SSA-PSO-BP神经网络均方根误差是0.38 mm，平均绝对百分误差为0.07%，相较于BP与PSO-BP神经网络模型精度有了进一步的提升，说明SSA-PSO-BP神经网络具有较好的全局精度。

4 结论

为解决航空壁板装夹变形预测问题，提出了一种Abaqus仿真与神经网络算法相结合的方式，并对神经网络进行了优化，实验结果表明，相较于传统的有限元模拟仿真，以及传统的BP神经网络，此次运用Abaqus与SSA-PSO-BP神经网络结合的这一结合思维，首先通过有限元仿真获取神经网络所需要的训练以及预测数据，其次通过对BP神经网络算法加以改进将其权值与阈值进行二次优化，最终表明构建的壁板装夹变形预测数字化模型具有很高的精度和很快的收敛速度，并且极大地减少了运算时间，提高了预测的效率。