LHC上J/ψ+一个喷注单举产生中长程矩阵元普适性研究
2023-12-19孙立平
孙立平
(北京建筑大学 理学院,北京 102627)
对重夸克偶素产生和衰变的研究一直是粒子物理学的重要任务,目前非相对论量子色动力学[1]是研究重夸克偶素的标准工具,而它的有效性则需要各种实验的检验[2-4]。在大型强子对撞机(LHC)上,J/ψ伴随一个喷注的单举产生具有重要意义:①此过程结合了重夸克偶素的产生以及喷注的性质;②此过程为单举过程,相对于遍举过程更加易于探测;③此过程非常适合于喷注物理的研究,可以用来研究喷注的结构,还可以用来检验各种喷注算法的合理性;④此过程可以用来萃取J/ψ的长程矩阵元。为了更好地理解重夸克偶素产生机制以及喷注的性质,需要在非相对论量子色动力学的次领头阶水平上来计算J/ψ伴随一个喷注的产生过程,相比领头阶,次领头阶不仅可以降低理论误差,而且可以存在新的动力学机制,比如大横动量行为和领头阶完全不同。因此,为了得到更精确的结果,在次领头阶水平上来计算J/ψ伴随一个喷注的单举产生过程。
1 理论框架
在非相对论量子色动力学中,LHC上J/ψ伴随一个喷注单举产生过程的截面可以表示为[1]

图1 J/ψ+1jet产生过程的领头阶和次领头阶典型费曼图
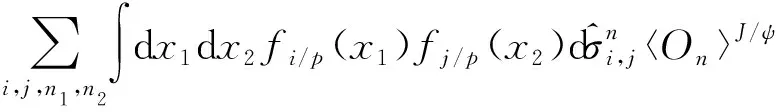
(1)
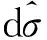
次领头阶修正过程可以分成2部分:虚修正和实修正。虚修正起源于对领头阶树图的单圈修正,而且仅包含胶子融合过程,这点和领头阶一样。而实修正除了胶子融合过程,还包含夸克胶子散射过程:q+g→J/ψ+1jet+q。
(2)
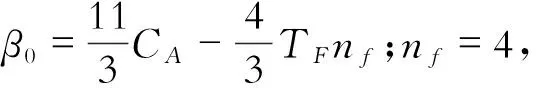
在实修正过程中存在2个子过程:g+g→J/ψ+1jet+g和q+g→J/ψ+1jet+q,由于末态相空间的积分,在这2个过程中都存在红外发散,这些红外发散会和虚修正中残留的红外发散,以及S波矩阵元的重整化发散互相抵消掉。根据相空间的不同区域,可以把红外发散分成软发散和共线发散。采用双截断相空间切片方法[5]来分离这2种类型的红外发散,最终实修正的截面可以表示为
(3)

通过标准的重整化步骤,再利用双截断相空间切片方法,最终可以把次领头阶J/ψ+1jet的产生截面表示为
σNLO=σBorn+σVirtual+σReal
(4)
其中紫外发散通过引入抵消项来消除,而虚修正和实修正中的红外发散,以及S波矩阵元的重整化发散会天然抵消掉,最终得到紫外、红外都有限的结果。
2 数值结果
2.1 参数输入
由于J/ψ+1jet单举产生过程次领头阶修正的复杂性,在计算中,利用了FEYNARTS[6]来产生此过程的所有费曼图和费曼振幅,利用VEGAS程序包进行相空间数值积分。
对于末态喷注,采用了anti-kt算法来进行重构,在程序中通过FastJet[7]包来实现,其中对应此算法的参数R=0.6,R为此算法中定义的一个半径参数。另外在anti-kt算法中,喷注是按横动量大小进行排序,领头喷注对应的横动量最大。
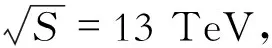



表1 长程矩阵元 10-2 GeV3
2.2 唯象分析
在大型强子对撞机LHC上,应用上述实验条件,可以得到p+p→J/ψ+1jet单举产生过程的总截面,见表2。
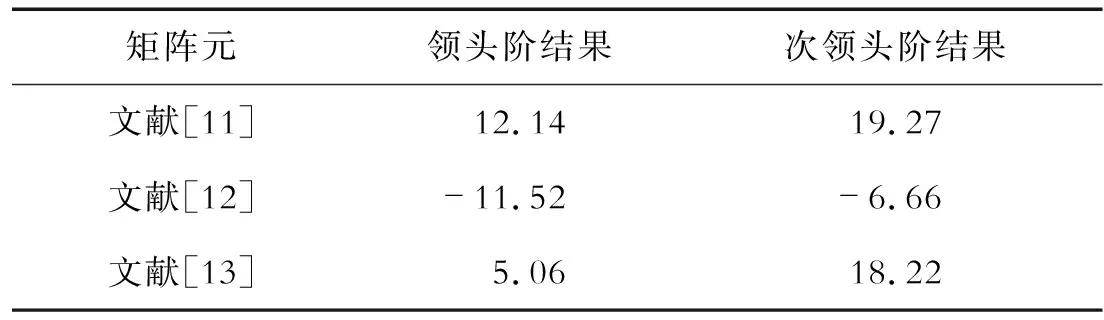
表2 领头阶和次领头阶总截面 nb
从总截面的结果来看,3个理论组拟合出的J/ψ色八重态长程矩阵元并不一致,甚至文献[12]的矩阵元给出的总截面是负值。这种不一致反映了在J/ψ单举产生过程中拟合出来的长程矩阵元并不是普适的,它们具有过程依赖性。然而,从表2的结果来看,抛开文献[12]负的截面不谈,文献[11]、文献[13]的矩阵元给出的截面,对于实验探测来说是很可观的,因此此过程的计算对于未来LHC此过程的探测提供了很好的理论预言。

(5)
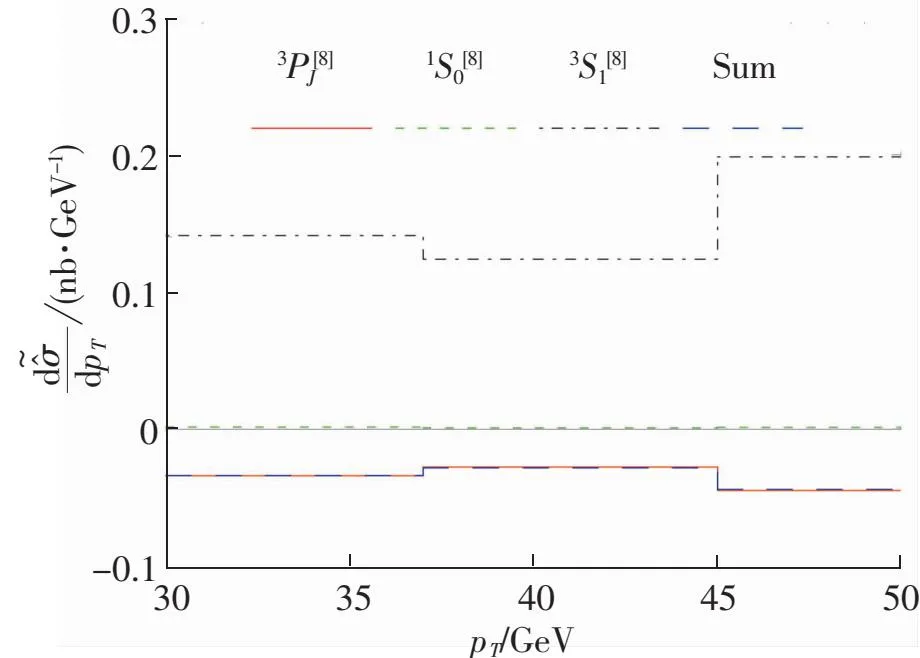
图的分解

(6)


表3 不同文献得到的和 GeV3
在p+p→J/ψ+1jet单举产生过程中,不同文献给出的矩阵元得到的结果不一致,这是一个非常重要的信息,它促使理论学家重新审视在J/ψ单举产生过程中拟合出来的长程矩阵元。这个现象表明在一个过程中拟合出来的矩阵元,还远远达不到普适性的要求,建议LHC将来能够测量J/ψ+1jet单举产生过程,然后将测得的实验数据,结合之前J/ψ单举产生等其他过程的数据,做一个多过程拟合,进而得到更精确、更普适的长程矩阵元。
3 结论
在非相对论量子色动力学框架下,研究了LHC上J/ψ伴随一个喷注单举产生的次领头阶修正,其中喷注的重构采用了anti-kt算法。首先应用标准重整化步骤,得到次领头阶水平上紫外、红外都安全的振幅模方,然后应用LHC上J/ψ和喷注的实验条件,进行相空间积分得到了此过程的产生截面。此工作的重点在于发现了应用不同理论组在J/ψ单举产生过程中拟合出来的矩阵元,得到的总截面并不一致,甚至其中一个组的矩阵元会导致负的截面值。这种不一致性,反映了目前通过实验数据拟合得到的矩阵元是过程依赖的。未来对矩阵元的期待有2点:①能有大的理论突破,算出矩阵元的普适值,当然这比较难实现;②期待LHC能探测J/ψ伴随一个喷注单举产生的过程,再结合之前J/ψ单举产生等其他过程的数据,进行多过程拟合,这样得到的矩阵元会比目前的更精确、更普适。
