熨平板振动压实特性与摊铺密实度控制方法研究

2023-12-18罗清云刘洪海

振动与冲击 2023年23期

罗清云, 吴平, 刘洪海, 贾洁

(1.长安大学道路施工技术与装备教育部重点实验室,西安 710064;2.内蒙古路桥集团有限责任公司,呼和浩特 010051)

在沥青路面施工过程中,摊铺机将沥青混合料摊铺、整形,得到一定尺寸和密实度的铺层[1]。熨平板是摊铺机工作装置的重要组成部分,熨平板工作参数对铺层材料密实度有重要的影响[2]。

国内外的研究表明,铺层材料密实度与熨平板振幅密切相关。罗丹建立了熨平板刚柔耦合的动力学模型,研究了熨平板横向振幅不均匀性对铺层横向密实度的影响[3];刘洪海等[4]基于共振理论,建立了铺层材料密实度与振动参数、系统参数之间关系的模型,得出熨平板振动频率与熨平板振幅、铺层材料密实度之间的关系;殷超等[5]通过虚拟样机仿真技术,研究振动器频率对熨平板箱体振幅响应的影响,确定了铺层密实度均匀性与平整度最佳时熨平板的工作参数;贾洁等[6]提出了夯锤和熨平板与铺层材料相互作用的动力学模型,得出了铺层材料密实度与夯锤频率、熨平板振动频率、铺层材料特性之间的关系;孙志刚[7]对加宽熨平板进行试验研究,采用ODS(operational deflection shape)形态、压力分布和加速度对熨平板系统的横向振动特性进行评价,提出了以压力分布为指标的铺层平整度、密实度的评价方法;Sun等[8]对双偏心轴熨平板振动机构进行研究,分析了熨平板工作参数对熨平板振动特性和压实特性的影响;Nguyen等[9-10]对熨平板系统建立非线性动力学模型,研究了熨平板振动的平稳性影响因素,优化了熨平板振动性能,提升铺层材料密实度的均匀性;Jia等[11]基于熨平板二自由度动力学模型,研究了熨平板振幅对铺层材料密实度的影响;以上研究通过对熨平板进行动力学分析,以熨平板的振幅为基础,得出铺层材料密实度随熨平板工作参数的变化规律。

摊铺机工作装置由振捣器和熨平板振动器构成,振捣器行程较大,其与混合料有周期性的接触分离,因此需对振捣器与混合料的相互作用进行研究。在已有研究的基础上,考虑振捣器与铺层材料的相互作用力对熨平板振动的影响,建立熨平板动力学模型;基于共振振动理论,提出铺层材料密实度与熨平板振幅的关系模型,给出铺层材料密实度的控制方法,通过工程试验对模型进行验证。

1 熨平板结构与工作原理

摊铺机工作装置的核心是熨平板,位于摊铺机后端,其功能是对混合料进行摊铺、抹平和初步振实。振动熨平板主要由振捣机构、振动器和箱体等组成,如图1所示。

1-箱体;2-偏心轴;3-振动机构;4-熨平板;5-振捣器。

振捣机构位于摊铺机熨平板前端,由振捣器和偏心轴等构成。液压马达通过传动装置驱动偏心轴转动,带动振捣梁做上下往复运动,对混合料产生捣固密实作用。振捣机构基于冲击振捣原理,对混合料进行密实。冲击振捣原理是通过低频高幅冲击作用对材料进行强制压缩,当冲击力产生的强度足够大时,铺层材料中产生的剪切力大于混合料之间的抗剪强度,能使材料颗粒相互交错重新排列,从而形成致密结构。

熨平板振动机构是一种平板型振动装置,位于摊铺机熨平板底部,通过液压马达驱动偏心轴转动,偏心轴转动产生离心力,离心力通过轴承座传递给箱体,使熨平板做上下往复运动,实现对混合料的熨平与振动密实。振动压实是在外载荷的重复作用下,激起被压实沥青混合料颗粒的振动,混合料产生的振动加速度减小了颗粒间的黏结和摩擦作用,在高频振动的作用下,被压沥青混合料重新进行排列,互相靠近,混合料内的空气被排除,密实度增加。

2 熨平板振动模型建立

2.1 夯锤振捣分析

振捣器安装在偏心轴上,偏心轴带动夯锤上下运动,对混合料进行捣实,因此可将夯锤简化为竖直方向的无约束平行运动,振捣器下部的混合料简化具有黏性阻尼的弹簧-质量模型,振捣器对混合料的捣实过程,如图2所示[12-14]。

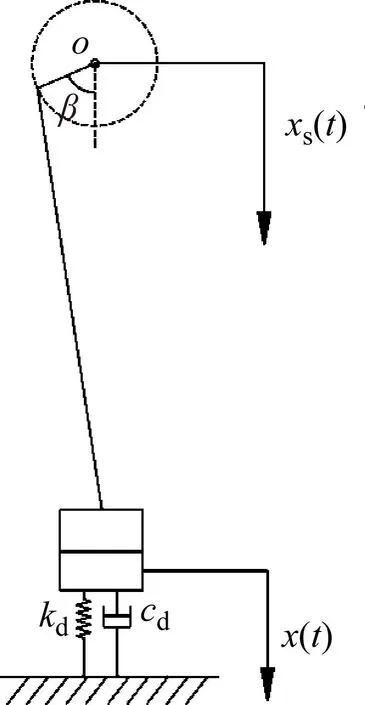
图2 振捣机构

图2中:o为偏心轴旋转中心;β为振捣器与混合料接触时振捣轴的旋转角;xs(t)为熨平板位移;x(t)为振捣器下部混合料位移;kd、cd为振捣器下部混合料的刚度系数与阻尼系数。

振捣机构对混合料进行振捣压实,在单次振捣过程中,振捣冲程较大,振捣器与混合料周期性的接触分离;当振捣轴旋转角为β时,振捣器与混合料接触,振捣器对混合料进行冲击捣实;由于振捣器的行程一定,与混合料接触的时间较短,混合料被快速压缩,因此可将振捣过程中混合料的压缩量简化为方波,如图3所示。

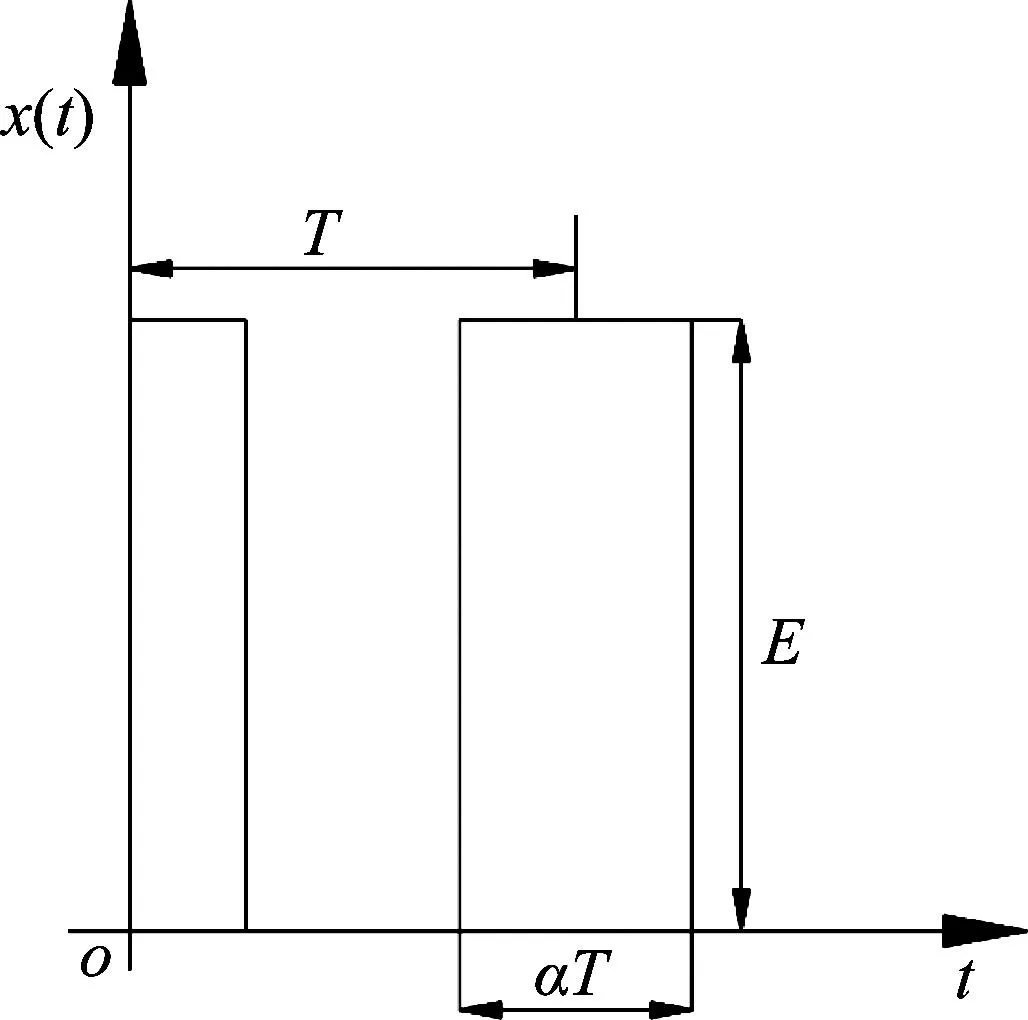
图3 周期性矩形波

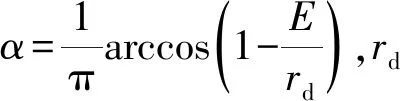
振捣过程中混合料的压缩量如下

(1)

采用傅里叶级数对混合料的压缩量进行展开,得到

(2)

式中,ωd为振捣器的偏心轴角速度,rad/s。

由于振捣器对混合料的压缩量为熨平板位移xs与振捣器位移xd之和,由式(2)可得振捣器位移、速度、加速度

(3)

对振捣机构进行受力分析,考虑振捣机构惯性力对熨平板的作用,得到振捣机构的动力学方程

(4)

式中:md为振捣器质量,kg;Fd为振捣器对偏心轴的力,N。

将式(3)代入式(4),可得振捣器对偏心轴的力

(5)

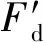
(6)

2.2 熨平板振动机构分析

熨平板振动机构由偏心轴、振动器与箱体构成,根据熨平板振动机构工作原理,对熨平板振动机构简化,并进行受力分析,如图4所示。

由于熨平板质量较大,水平方向受牵引大臂的约束,忽略熨平板的前后摆动,仅考虑熨平板在竖直方向的运动,得到熨平板振动机构的动力学微分方程

(7)

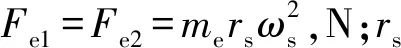
将式(5)、式(6)代入式(7),化简后得

(8)

式中:m为熨平板系统质量,m=ms+2me-md,kg;c为熨平板系统阻尼,c=cs-cd,N·s/m;k=ks-kd,N/m。

根据线性系统叠加原理,由式(8)可求得熨平板稳态的位移、加速度

(9)

(10)

由式(9)和式(10)可知,熨平板的振动特性与熨平板质量、振捣器结构参数、铺层材料刚度与阻尼、熨平板振动频率及振捣器频率等因素有关;熨平板的位移、速度、加速度由熨平板振动频率、振捣频率与振捣频率倍频等多个频率分量构成;振捣器频率分量的幅值与振捣频率、铺层材料特性有关;随着振捣频率降低,熨平板振动频率的增加,振捣器主频与熨平板振动主频幅值比减小,振捣器对熨平板振动的影响减小。

3 熨平板振幅与摊铺密实度关系模型

摊铺机摊铺沥青混合料时,通过夯锤的低频振捣,松散混合料初步形成骨架结构;熨平板振动机构采用高频振动的方式,对混合料进一步压实。根据混合料在摊铺过程中呈现的状态,可将摊铺压实过程分为塑性阶段和弹塑性阶段:在塑性阶段,混合料较为松散,此时宜采用低频高幅的振捣方式,对混合料产生强制压缩作用,减小混合料空隙率,使混合料的粗骨料相互接触,形成基本骨架;在弹塑性阶段,混合料具有一定的弹性模量和剪切模量,熨平板的振动能量可传递到混合料内部,在熨平板高频振动作用下,混合料内部的粗集料和细集料随着熨平板振动产生高频颤振,集料颗粒重新排列,粗集料间的空隙被细集料和沥青胶浆填满,混合料被逐步密实,材料塑性降低,弹性增大[15-19]。

方波傅里叶变换的前三项占据了方波总能量的80%,因此将n取为2,由式(9)可得熨平板各个频率分量的幅值

(11)

(12)

(13)

式中:As为熨平板振动频率分量的幅值,m;Ad1为熨平板位移中振捣频率分量的幅值,m;Ad2为熨平板位移中二倍振捣频率分量的幅值,m。

由式(9)、式(11)～式(13)可知,熨平板位移包含多个频率分量,与各因素关系复杂,可通过数值计算方法求取。将熨平板幅值A与振动频率、阻尼比、固有频率的变化规律如下

A=f(ωs,ζ,ωm)

(14)

共振压实理论认为,当压实设备与被压材料共振时,被压材料的振幅最大,压实效果最好,被压材料的密实度较高。基于共振压实理论,结合式(9)、式(14),可建立熨平板振幅与铺层材料密实度P之间的关系

P=P0+P1A

(15)

式中:P0为常数项;P1为熨平板振幅对铺层材料密实度的影响系数。

4 熨平板仿真分析

以中大DT1600型沥青摊铺机为研究对象,将振捣频率设为定值,对熨平板进行振动仿真,分析熨平板的振动特性,研究熨平板压实特性与振动频率、铺层材料刚度和阻尼之间的关系。

4.1 熨平板振动仿真

熨平板仿真参数通过参考文献和现场试验确定,如表1所示。

表1 仿真参数

对熨平板振动模型进行仿真,可得熨平板的位移、加速度,并对熨平板加速度进行傅里叶变换,仿真结果如图5所示。

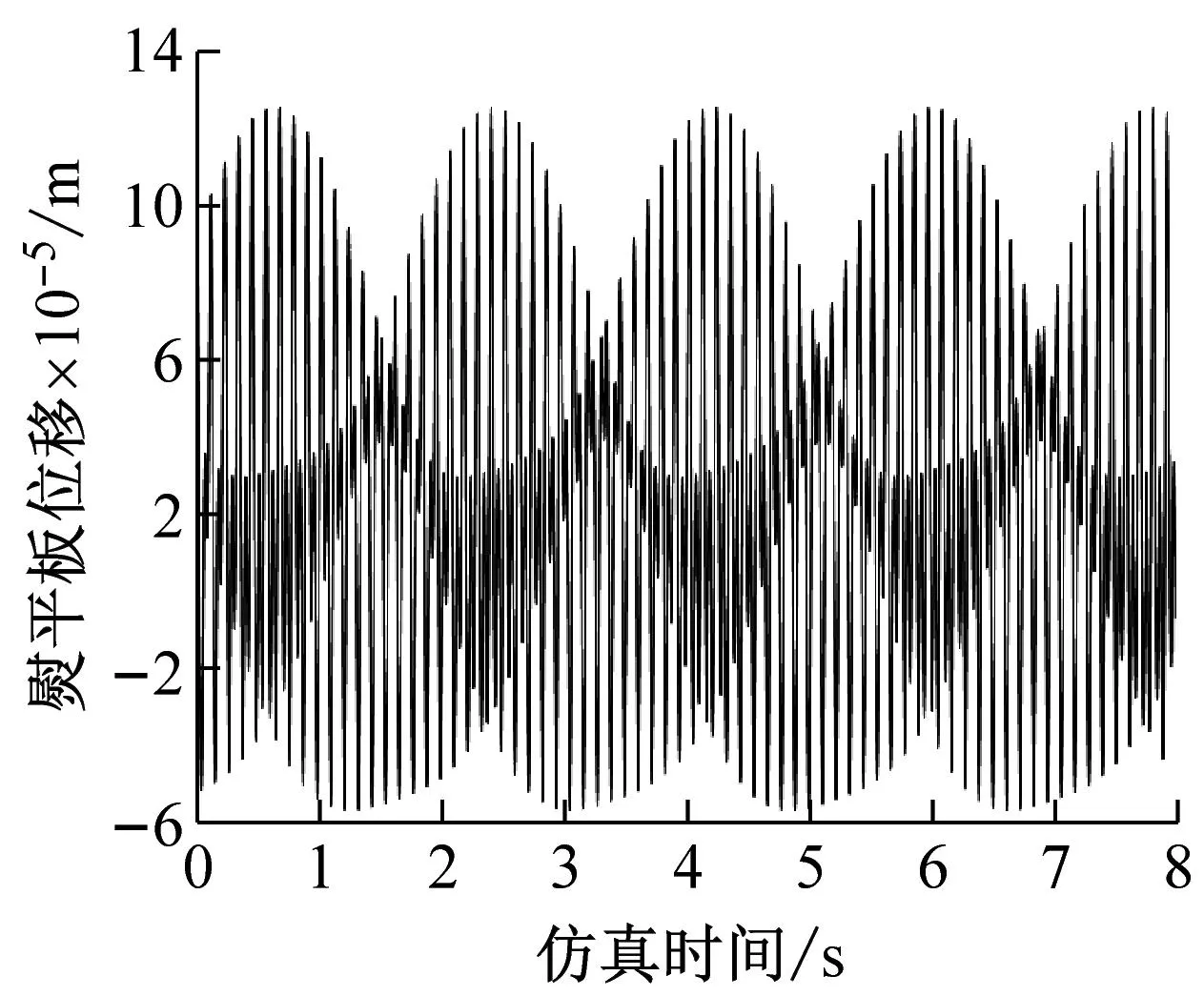
(a) 熨平板位移

由图5(a)可知,熨平板位移仿真结果可知,熨平板实际振幅较小,约为1.82×10-4m。该型摊铺机的振捣器行程为0.006 m,熨平板振幅占振捣器行程的3.03%,熨平板振动对振捣器运动的影响较小,因此可以通过解耦的方式,对振捣器与熨平板振动机构进行分析,建立熨平板振动模型。由图5(c)可知,熨平板加速度傅里叶变换结果可知,熨平板振动频谱包含了熨平板振动频率、振捣主频及其倍频分量。

当振捣频率一定,熨平板振动频率增加时,得到熨平板加速度傅里叶变换结果,如图6所示。

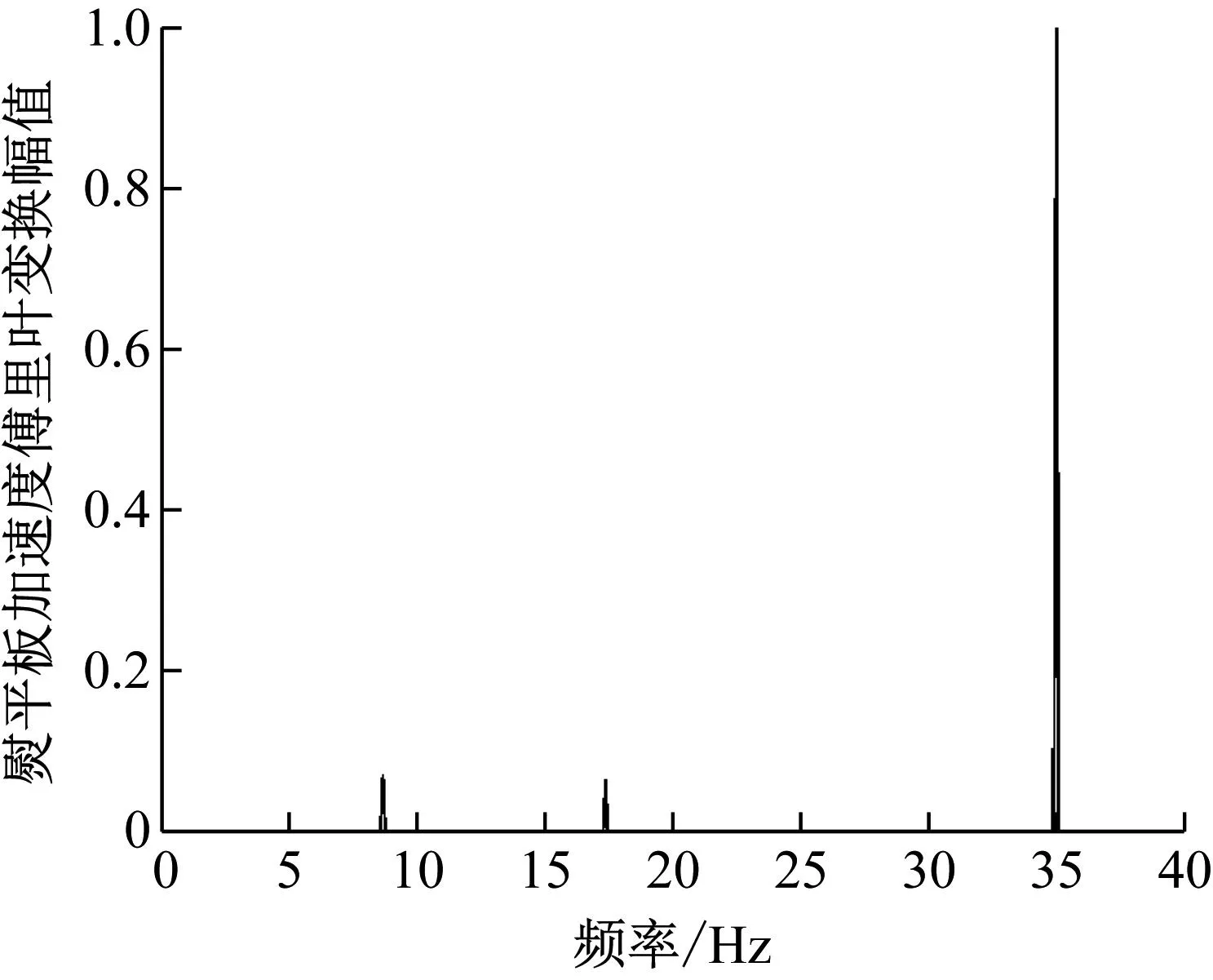
图6 振动频率35 Hz,熨平板加速度傅里叶变换

由图5(c)与图6可知,当振捣频率一定时,随着熨平板振动频率增加,振捣频率主频及其倍频的幅值与熨平板主频幅值比减小,振捣器对熨平板振动的影响降低。

4.2 熨平板压实特性仿真研究

熨平板压实特性与压实系统的固有频率及阻尼有关:混合料的沥青用量越多,铺层材料的阻尼越大,压实系统的阻尼比越高;粗集料占比越大,压实系统的固有频率越低;因此需对铺层材料特性对熨平板振动情况进行仿真研究。

对于固有频率为32 Hz的压实系统,阻尼比变化时,对熨平板的振动特性进行仿真,由式(14)可得到熨平板振幅与振动频率之间的关系,如图7所示。

图7 固有频率一定,熨平板振幅与振动频率关系

由图7可知,压实系统的阻尼比较小时,熨平板振幅随振动频率的增加而增大,在最佳压实频率附近达到最大值,熨平板的振动频率继续增加,熨平板振幅有一定的减小,熨平板振幅会出现明显的峰值,熨平板对铺层材料有一段高效压实区域;随着阻尼比的增加,熨平板振幅随振动频率增加而增大,没有明显的高效压实区域,当振动频率大于35 Hz,熨平板振幅趋于稳定,熨平板压实效果最佳。

压实系统的阻尼比为0.49,固有频率变化时,熨平板振幅与振动频率之间的关系如图8所示。

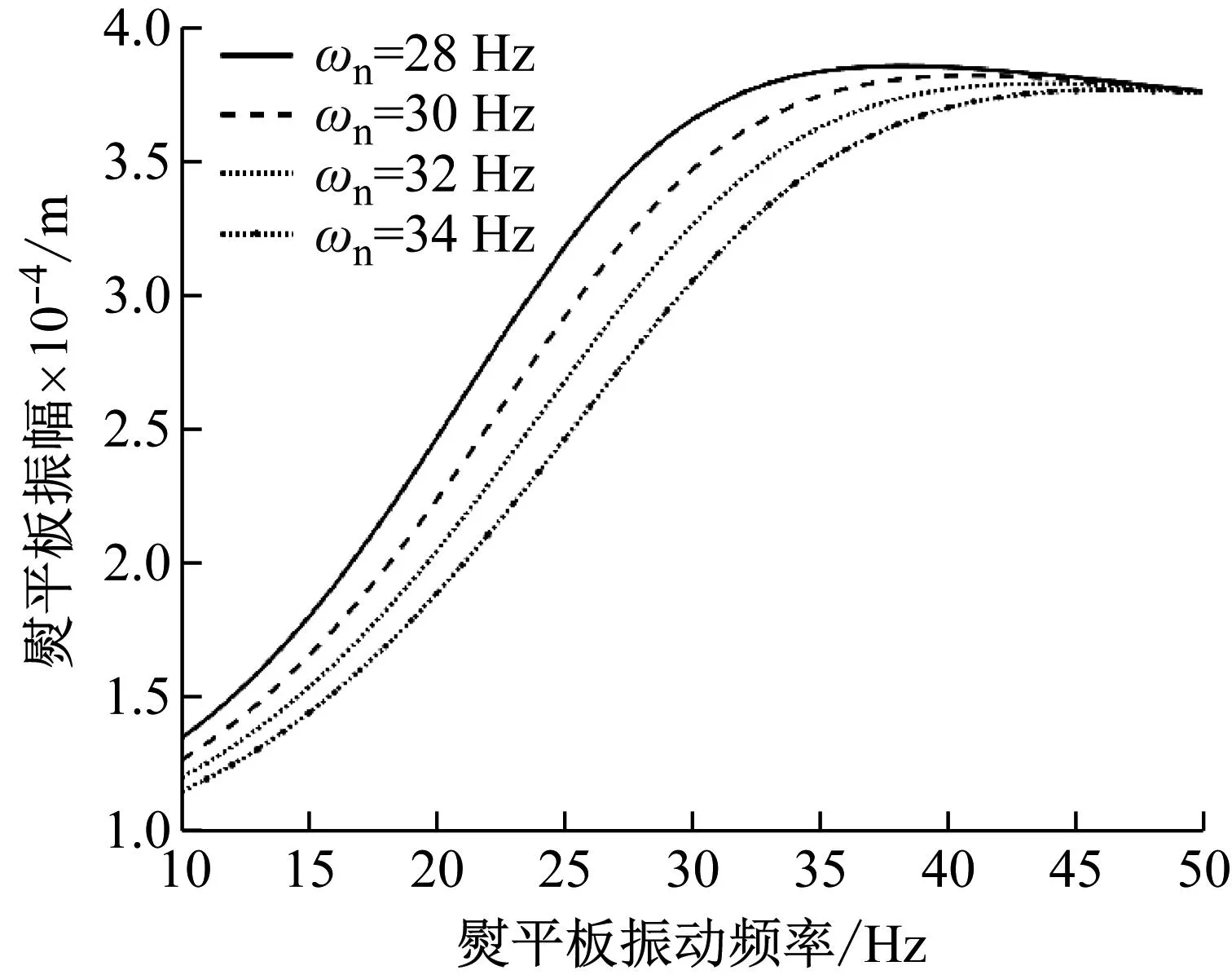
图8 阻尼比一定,熨平板振幅与振动频率关系

由图8可知,压实系统阻尼比一定,粗集料比例减小,固有频率增大,对应的最佳压实频率增加;当铺层材料粗集料含量较少,系统固有频率较高时,采用较高的振动频率可提升铺层材料压实效果;当系统固有频率为32 Hz时,熨平板振幅的最大位置在42 Hz处,熨平板振幅最大处对应的频率大于系统固有频率,摊铺施工时,熨平板的压实频率应大于系统固有频率,以实现铺层材料的高效压实。

由图7、图8可知,当熨平板振动频率由10 Hz增加到35 Hz时,熨平板振幅随之增大,通过调整熨平板的振动频率,可以改变熨平板振幅,实现铺层材料密实度的控制。

熨平板质量较重,在振动过程中始终与混合料接触,因此将熨平板对混合料的压实作用简化为弹簧单自由度的黏弹性的熨平板子系统;在混合料的捣实过程中,振捣器行程较大,与混合料周期性的接触与分离,导致系统产生了非线性;为了简化振捣器受到的混合料周期性冲击力作用,通过对熨平板振动分析,熨平板的振幅较小,为1×10-4m量级,振捣器的行程为 6×10-3m,熨平板振幅比夯锤行程低了一个量级,因此忽略了熨平板位移对振捣器与混合料接触的影响,将混合料的压缩量简化为方波形式,计算出振捣器对熨平板的作用力Fd,最终建立了熨平板振动模型,见式(8);模型中的误差为熨平板振动对振捣器与混合料接触的影响,为了分析该影响,熨平板最大振幅约为4×10-4m,因此将混合料的压缩量E由2×10-3m增加至2.4×10-3m(见图7),得出熨平板振幅与振动频率的关系曲线,如图9所示。

图9 混合料压缩量与熨平板振幅关系

图10 沥青混合料级配曲线

由图9可知,混合料压缩量的增大对熨平板振幅与熨平板振动频率变化趋势影响较小;熨平板振动频率较低时,熨平板振幅较小,此时可参考E取2.15×10-3m的曲线,以E=2.00×10-3m的熨平板振幅为基准,估算振幅误差,熨平板振动频率取为10 Hz,熨平板振幅绝对误差为6.10×10-6m,相对误差为5.09%;熨平板振动频率较高时,熨平板振幅较大,此时参考E为2.40×10-3m的曲线,熨平板振动频率取为50 Hz,熨平板振幅绝对误差为1.65×10-5m,相对误差为4.43%;以上研究表明,振捣器捣实混合料对熨平板的振动影响较小,因此可对振捣器和熨平板解耦,分别对振捣器和熨平板进行分析。

5 试验研究

摊铺机熨平装置的振动状态与铺层材料和熨平板工作参数有关,是熨平板装置与铺层材料组成系统的特性,因此熨平板装置的振动特性需通过现场试验确定。以中大DT1600型沥青摊铺机为试验对象,振捣器的工作频率范围为0～20 Hz,熨平板振动机构的工作频率范围为0～50 Hz。试验材料为AC25,沥青选用90#A级道路沥青,含量为4.3%,沥青混合料的级配如图9所示。

摊铺速度设定为2.5 m/min,振捣器的工作频率为8.7 Hz,熨平板的振动频率在10～45 Hz范围内进行调整。

5.1 熨平板振动特性试验研究

在摊铺施工过程中,熨平板振动频率设定为18 Hz,采用压电加速度传感器检测熨平板振动加速度,通过采集卡采集熨平板加速度信号,对采集的信号滤波处理,进行傅里叶变换,得到熨平板加速度信号的频谱图。摊铺试验现场如图11所示。

图11 试验现场

加速度传感器采用磁吸底座,吸附在摊铺机熨平板后沿,安装位置如图12所示。

对采集的加速度信号进行滤波处理,熨平板的试验加速度与仿真加速度的对比如图13所示。

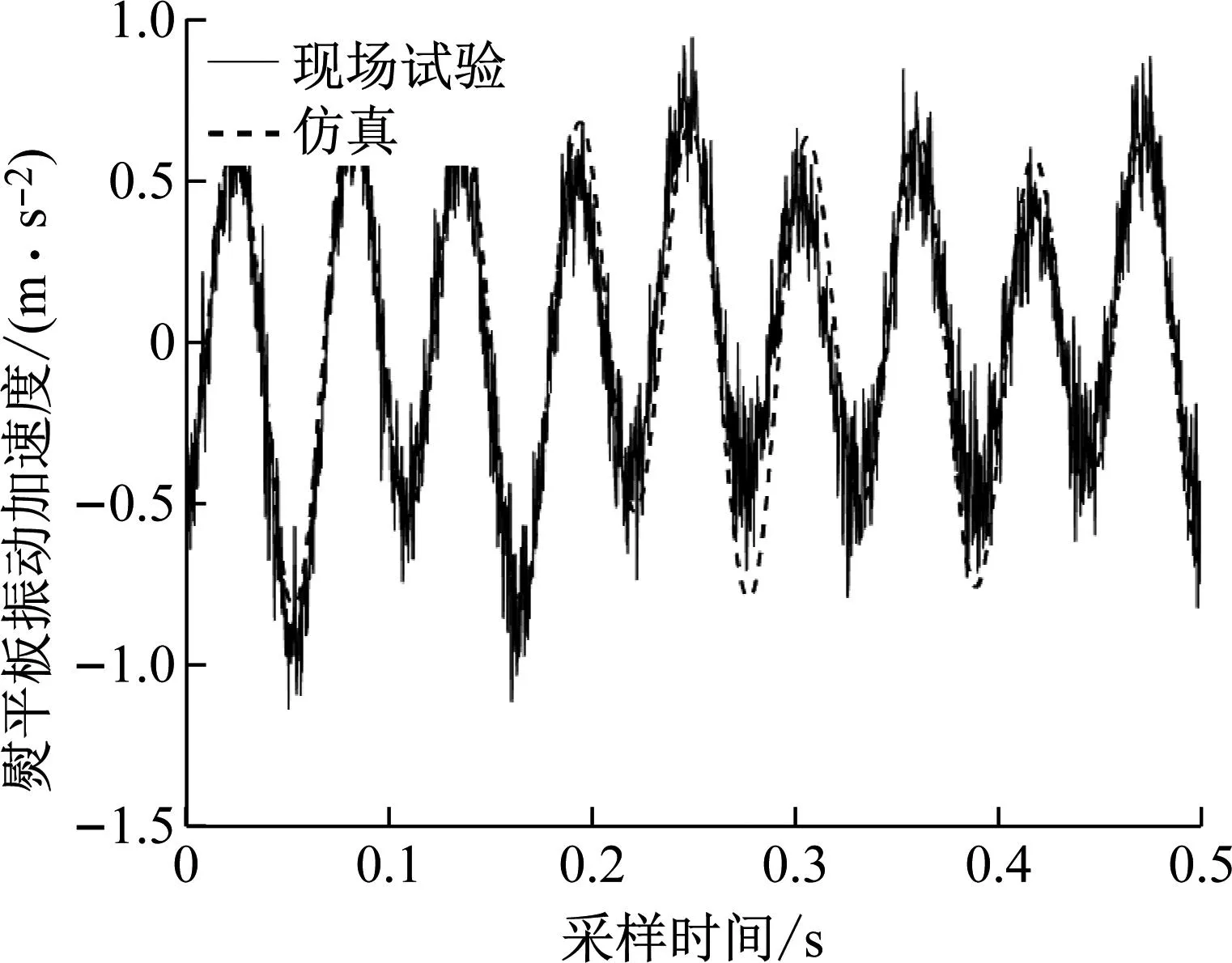
图13 熨平板振动加速度仿真结果与现场试验对比

对熨平板加速度进行傅里叶变换,仿真加速度与试验加速度傅里叶变换结果如图14所示。

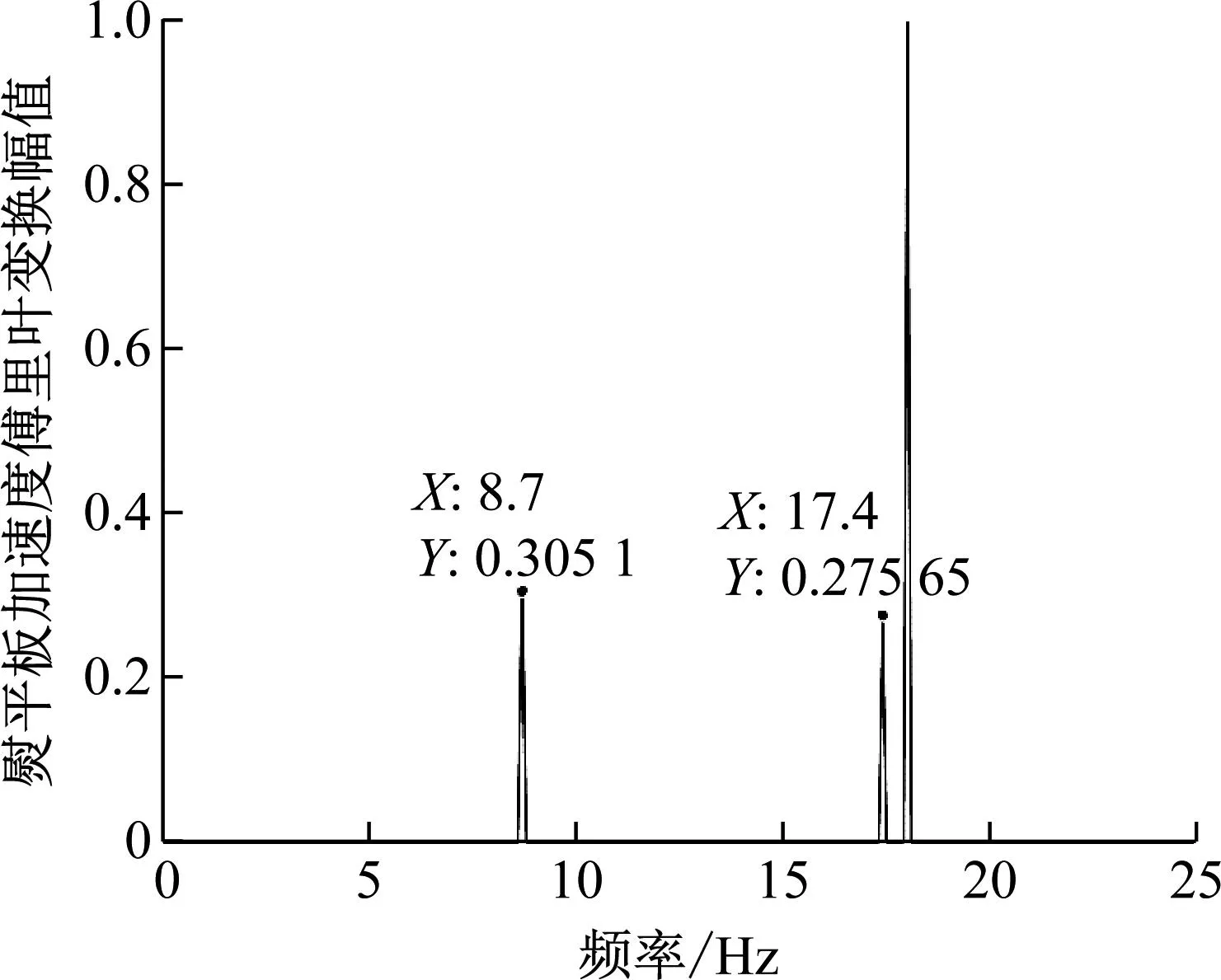
(a) 仿真结果

由图13可知,熨平板试验加速度与仿真加速度的变化情况基本一致。由图14可知,现场试验中熨平板加速度信号的傅里叶变换结果包含振捣主频、振捣频率两倍频多个频率;由式(10)与熨平板加速度仿真结果可知,熨平板系统包含多个频率;试验得到的加速度频谱图与仿真结果较为一致,表明模型具有实用性,模型参数取值有效。

5.2 熨平板压实特性试验研究

熨平装置的压实效果与熨平板工作参数和铺层材料有关,是熨平板与铺层材料相互作用的结果,需通过现场试验进行研究。试验过程中,摊铺速度设定为2.5 m/min,熨平板的振动频率在10～45 Hz范围内进行调整。使用已标定的PQI301型无核密度仪对同一位置铺层材料进行4次测量,取平均值,得到铺层材料密实度。采用最小二乘法对试验数据与仿真数据进行拟合,求取模型参数,得到式(15)中P0=79.92,P1=2.09×104。铺层材料密实度、熨平板振幅与熨平板振动频率之间的关系如图15所示。

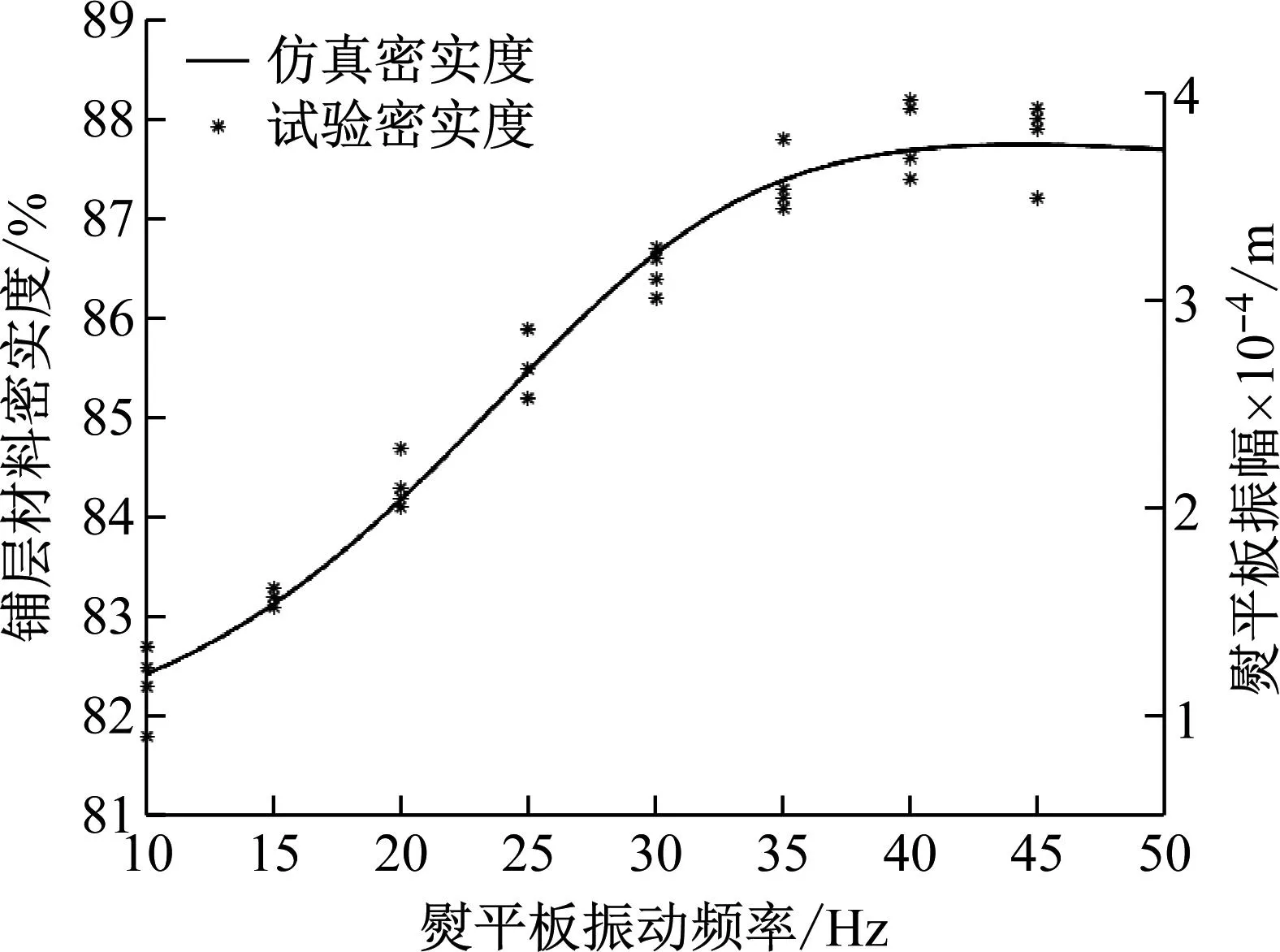
图15 材料密实度、熨平板振幅与振动频率的关系

由图15可知,随着熨平板振动频率的增加,熨平板振幅增大,铺层材料的密实度变大;当熨平板振动频率超过最佳压实频率时,熨平板振幅有一定程度的降低,铺层材料密实度随之减小;熨平板振动频率在10～35 Hz范围时,对熨平板振动频率与铺层材料密实度进行线性拟合分析,拟合优度为0.99,熨平板振动频率每增加5 Hz,铺层材料密实度提升1.09%;试验结果与仿真结果相符,通过调整熨平板的振动频率,可实现铺层材料密实度的控制。