Si3N4陶瓷纵扭超声磨削表面残余应力及其试验研究

闫艳燕, 秦飞跃, 张亚飞, 马千里, 王晓博

(河南理工大学 机械与动力工程学院,河南 焦作 454003)

Si3N4陶瓷具有高硬度、高导热性和耐高温等优异的材料性能,因此被广泛应用于航空航天、汽车和电子等行业[1-2]。但Si3N4陶瓷较高的硬脆性使其在传统磨削加工中容易出现微裂纹,引起亚表面损伤,对陶瓷零件的使用性能影响较大[3-4],进而限制了陶瓷零件在航空航天、国防工业及电子信息等高科技技术领域中的应用。

目前,高性能陶瓷零件的高效超精密磨削技术已成为精密超精密加工领域的研究热点。国内外众多学者采用激光、电化学、超声等特种加工技术及其复合加工技术对陶瓷材料高效超精密磨削进行了大量的研究[5-7]。其中,超声磨削因其具有能量集中、瞬间作用、快速切削的特性,能有效地改变传统加工的切削机制,具有独特的加工效果,非常适用于高性能陶瓷零件的精密超精密加工[8-9]。荆君涛等[10]建立了Si3N4陶瓷摩擦因数分形模型,研究了旋转超声磨削Si3N4陶瓷加工中表面形貌和摩擦因素的变化规律,为提高陶瓷耐磨性提供参考。Jing等[11]基于BP神经网络对Si3N4陶瓷旋转超声磨削表面形貌模型进行研究,建立了表面形貌与工艺参数之间的神经网络模型,该算法可以为表面形貌优化提供依据。Li等[12]基于超声振动辅助磨削轨迹和划痕试验,建立了法向磨削力的理论模型,研究了超声振动辅助磨削Si3N4陶瓷的去除机理,发现超声振动辅助磨削有利于提高其表面质量。Baraheni等[13]建立了旋转超声辅助端面磨削Si3N4陶瓷亚表面损伤深度预测模型,发现该模型能够预测陶瓷材料中的亚表面损伤深度。与普通磨削相比,旋转超声辅助端面磨削的亚表面损伤深度可减少30%。Baraheni等[14]建立了旋转超声辅助端面磨削Si3N4陶瓷切削力数学模型,分析了旋转超声辅助端面磨削Si3N4陶瓷的切削力,与普通磨削相比,旋转超声辅助端面磨削Si3N4陶瓷的切削力降低了64%。Yan等[15]分析了二维超声振动辅助磨削材料独特的去除过程,建立了二维超声振动辅助磨削陶瓷的三维粗糙度预测模型,为预测硬脆材料超精密加工表面质量提供参考。Qiao等[16]从切削力、划痕形貌和去除形式比较了传统磨削和超声振动辅助磨削Si3N4陶瓷的不同,分析了超声振动下Si3N4陶瓷材料的去除机理和裂纹抑制效果,发现随着划痕间距的增加,划痕之间的裂纹抑制作用逐渐减小。

综上所述,国内外学者们通过理论、仿真及试验的方法对Si3N4陶瓷超声磨削加工机理和表面形貌进行了大量研究,发现Si3N4陶瓷表面亚表面微裂纹对零件的使用性能具有较大影响,而残余应力是影响表面亚表面微裂纹产生与扩展的主要原因之一,是衡量表面完整性的评价指标之一[17-18]。但是超声磨削Si3N4陶瓷表面残余应力的研究较少,目前尚未形成系统的理论。在此背景下,为了深入研究纵扭超声磨削Si3N4陶瓷表面亚表面损伤机理,以纵扭超声磨削残余应力理论模型的建立为切入点,对纵扭超声磨削Si3N4陶瓷表面残余应力的形成机理和分布机制进行研究,旨在为提高陶瓷零件抗疲劳性提供一定的理论基础和参考依据。

1 Si3N4陶瓷纵扭超声磨削表面残余应力分析

1.1 纵扭超声磨削单颗磨粒运动特性分析

纵扭超声磨削示意图如图1所示。根据图1,单颗磨粒的运动由砂轮绕主轴的匀速圆周运动、相对工件的往复运动以及沿砂轮的超声振动组成。任意选取砂轮表面某一磨粒P,以砂轮中心为坐标原点O,建立空间直角坐标系(见图1(a)),假设磨粒P在P1处与工件开始接触,在P2处与工件分离,则纵扭超声磨削过程中单颗磨粒P的切削轨迹为

(1)

式中:vw为工件的进给速度(mm/s);ns为主轴转速(r/min);fθ为扭振方向的频率(Hz);fa为砂轮轴向的纵振频率(Hz);Aθ为扭振方向的振幅(μm);Aa为砂轮轴向的纵振幅值(μm);Φ为复合振动间的相位差(rad);t为磨粒与工件接触时刻(s)。

根据式(1),可仿真出普通磨削和纵扭超声磨削过程中单颗磨粒的切削轨迹,如图2所示。由图2可知,普通磨削过程中单颗磨粒的切削轨迹为直线,而纵扭超声磨削过程中单颗磨粒的切削轨迹为椭螺线,这样独特的切削轨迹更有利于在零件表面获得较好的加工质量。

图2 单颗磨粒的切削轨迹

根据图1(b)和式(1),单颗磨粒在P1处的线速度vθ可表示为

vθ(t)=vs+Aθωθcos(ωθt)=vs+2πfθAθcos(2πfθt)

(2)

式中,vs为砂轮线速度(mm/s)。

根据式(2),砂轮相对工件的速度vr为

(3)

式中:φ为单颗磨粒从P1到P2旋转经过的角度(rad),φ=ωst+(Aθ/R)sinωθt。

由于超精密磨削过程中,φ角极小,故cosφ≈1,则式(3)可简化为

vr(t)=vs+2πfθAθcos(2πfθt)+vw

(4)

根据式(4)可知,磨粒沿工件进给方向的切削速度随时间发生周期性变化。当vs+vw>2πfθAθ时,超声振动方向与砂轮旋转方向相同,磨粒相对工件进给速度增加,使得磨粒提前离开磨削区,减小磨粒对工件的作用时间。当vs+vw<2πfθAθ时,磨粒的瞬时切削速度小于零,使得单颗磨粒与工件在磨削区域产生高频振动分离现象,同时磨粒对已加工区域表面产生熨压作用,有利于零件表面质量的提高。

1.2 Si3N4陶瓷纵扭超声磨削表面残余应力分析

在陶瓷材料的磨削加工过程中,外部所施加的载荷通过磨粒作用于工件表面,导致材料产生局部的塑性变形,因而在陶瓷材料表面产生一个复杂的弹/塑性应力场。单颗磨粒压痕应力场模型,如图3所示。

图3 单颗磨粒压痕应力场模型

由图3可知,当磨粒受到法向集中载荷作用后,会在接触区域产生局部的塑性变形,Yoffe提出将压痕塑性核周围的应力场称为泡罩场,而满载状态下压痕应力场是由泡罩场和Boussinesq场组成,而卸载后的残余应力场仅为泡罩场,压痕应力场可表示为[19-21]

(5)

式中:αij为Boussinesq应力场;βij为泡罩应力场;P为集中力(N);R为应力场中任意一点到接触点的距离(μm);φ为R与z轴之间的夹角(rad);θ为R在xoy平面内的投影与x轴之间的夹角(rad);ν为陶瓷材料的泊松比;B为Blister应力场强度。

Blister应力场强度B可表示为[22]

(6)

式中:E为材料的弹性模量(GPa);ΔV为致密化变形体积,ΔV=fV;f为材料致密化变形体积与压痕体积比;维氏压痕V=2a3/3tanφ,a为磨粒与工件接触半径(μm)。

将式(6)代入式(5)可得普通磨削时磨粒与工件接触点附近的压痕应力场表示为如下通式形式

(7)

与普通磨削相比,纵扭超声磨削时,磨粒与工件接触面之间的磨削力由连续的挤压力变为脉冲力,在实际磨削过程中法向磨削力可表示为[23]

(8)

式中:ξ=1.85;h表示平均未变形切屑厚度;Hv表示维氏硬度(GPa)。

平均未变形切屑厚度h可表示为[24]

(9)

式中:C为砂轮单位面积上有效切点数,C=3.2 grit/mm2;r为切屑形状因子,一般情况下取值为10;de为砂轮当量直径(mm)。

将式(2)、式(9)代入式(8),则纵扭超声磨削时磨粒与工件之间的法向磨削力FN为

(10)

根据式(10)可知,纵扭超声磨削时,磨削力的大小与超声加工参数有关。由于纵扭超声振动的引入,平均未变形切屑厚度减小,从而使磨削力减小。

将式(10)代入式(7)可得纵扭超声磨削单颗磨粒压痕应力场表达式

(11)

根据式(11)可知,单颗磨粒接触区内部任一点R0处应力场的大小与磨削力的参数、磨粒的半顶角δ以及失角函数有关。在纵扭超声磨削工件过程中,由于磨粒对工件的脉冲切削力是周期性变化的,因此,在材料内部形成的是一个交变应力场,这会促使材料疲劳破坏,从而使得材料更容易去除。

在卸载过程中,随着纵扭超声磨削力减小,由弹性变形产生的弹性应力场逐渐减小至0,而塑性变形是不可逆的,所以由局部塑性变形产生的应力残留在材料内部形成残余应力。

当硬脆材料表面无残余应力时,其断裂韧性KIC可表示为[25]

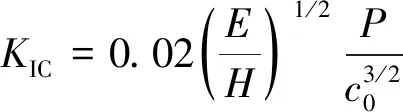
(12)

式中:H为维氏硬度(MPa);P为压痕载荷;c0为裂纹长度。

当硬脆材料表面出现残余应力时,压痕中的裂纹长度将会受到影响,此时考虑残余应力对压痕应力场的影响,其断裂韧性KIC可表示为[26]

(13)

式中:c1为裂纹长度;Y为应力强度系数,可取1.29。

结合式(12)和式(13),硬脆材料表面残余应力表达式为

(14)

根据式(14),对Si3N4陶瓷纵扭超声磨削下表面残余应力进行仿真计算,材料的力学性能见表1,不同磨削参数下Si3N4陶瓷表面残余应力仿真计算结果如图4所示。由图4可知,普通磨削(超声振幅A=0)后,加工表面残余应力表现为拉应力,而纵扭超声磨削后,加工表面残余应力表现为压应力。从图4中可以发现,纵扭超声磨削时,残余压应力随着超声振幅增大呈现明显增大趋势,随着磨削深度增大呈现明显减小趋势,随着砂轮转速增大呈现缓慢增大趋势,随着进给速度增大呈现缓慢减小趋势。

表1 Si3N4陶瓷的力学性能

(a) 超声振幅对残余应力的影响

2 Si3N4陶瓷纵扭超声磨削试验

2.1 试验设计

本文搭建了纵扭超声磨削Si3N4陶瓷试验平台,磨削试验采用侧面铣磨的加工方式,磨削过程中加入磨削液,试验平台如图5所示。由图5可知,试验平台由三轴立式加工中心(VMC 850E)、纵扭超声振动系统和数据采集系统组成,其中超声振动系统由35 kHz超声波发生器、无线传输装置、BT40刀柄、压电陶瓷换能器以及纵扭复合圆锥形变幅杆等组成,磨削砂轮为200#树脂基金刚石砂轮,试验时通过超声波发生器的开关实现纵扭超声磨削与普通磨削的变换。工件选用Si3N4陶瓷材料,规格为10 mm×15 mm×5 mm,主要力学性能参数如表1所示。

图5 纵扭超声磨削试验平台

为分析工艺参数对磨削后残余应力和表面形貌的影响,采用单因素磨削试验,试验方案如表2所示。为提高试验结果的准确性,试验前首先对待加工表面进行粗磨找平,进行多次光磨,随后使用1 μm的切深多次进给,直至采集到的磨削力信号稳定无明显变化。本试验采用X射线衍射仪测量Si3N4陶瓷磨削后表面残余应力,残余应力的测试条件如表3所示。本试验选用截面抛光法对加工后的试件进行处理,并使用扫描电子显微镜(SEM)观测工件亚表面的形貌特征。

表2 磨削试验方案(f=35 kHz)

表3 X射线衍射仪测试条件

2.2 结果分析

2.2.1 Si3N4陶瓷表面残余应力分析

Si3N4陶瓷表面残余应力试验结果,如图6所示。从图6可知,普通磨削加工后表面残余应力为拉应力,而纵扭超声磨削加工后表面残余应力为压应力,且Si3N4陶瓷表面残余应力试验结果与理论仿真误差不超过10%,两者趋势一致。

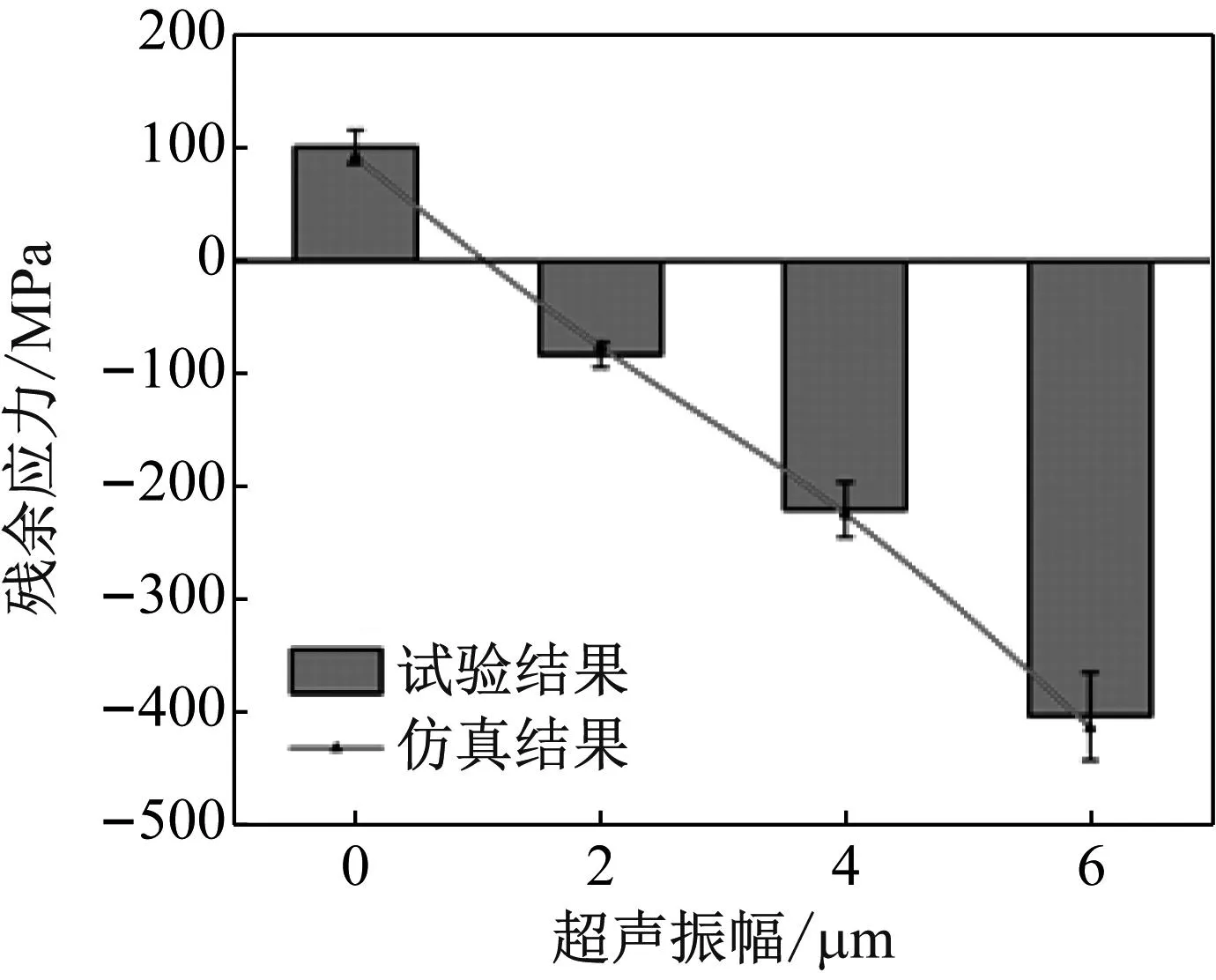
(a) 超声振幅对残余应力的影响

由图6(a)可知,工件表面残余压应力随着纵扭超声振幅的增大呈现增大趋势。在纵扭超声冲击的作用下,磨粒在切削过程中存在反向切削特性,对已加工表面进行多次熨压,并且随着超声振幅的增大,磨粒冲击和挤压作用越强,使得工件表面残余压应力呈现增大趋势。由图6(b)可知,工件表面残余压应力随着磨削深度的增大呈现减小趋势。由于磨削深度的增加,平均未变形切屑厚度增大,导致磨削力不断增大,使得工件表面残余压应力呈现减小的趋势。由图6(c)可知,工件表面残余压应力随着砂轮转速的增大呈现增大趋势。这是由于砂轮转速的不断增加,使磨粒相对工件的切削速度不断增加,则平均未变形切屑厚度减小,磨削力将会减小,使得工件表面残余压应力呈现增大的趋势。由图6(d)可知,工件表面残余压应力随着进给速度的增大呈现减小趋势。这是由于随着进给速度的增加,磨粒与工件之间的摩擦作用增强,平均未变形切屑厚度增大,磨削力增大,使得工件表面残余压应力呈现减小的趋势。

2.2.2 Si3N4陶瓷亚表面微观形貌分析

Si3N4陶瓷磨削后亚表面微观形貌,如图7所示。由图7(a)可知,普通磨削后,Si3N4陶瓷亚表面出现凹坑和较长的裂纹,这是由于普通磨削时磨削力较大,Si3N4陶瓷表面残余应力为拉应力,所以导致亚表面出现凹坑和较长的裂纹,进而影响材料的使用性能。由图7(b)可知,纵扭超声磨削后,Si3N4陶瓷亚表面出现轻微凹坑,裂纹深度减小。这是由于纵扭超声振动的引入,磨粒的高频冲击作用使得材料以粉末状、碎屑状去除,同时磨削力减小,出现熨压作用,使得Si3N4陶瓷表面残余应力为压应力,从而使裂纹深度减小。

由图7(b)、图7(c)和图7(d)可知,随着超声振幅不断增大,Si3N4陶瓷亚表面出现轻微凹坑,裂纹深度不断减小。与普通磨削相比,纵扭超声磨削后Si3N4陶瓷亚表面损伤深度最大可降低38%,这是由于随着超声振幅的增大,磨粒冲击和挤压作用越强,对已加工表面进行多次熨压,使得Si3N4陶瓷表面残余压应力增大,能在一定程度上抑制表面微裂纹扩展,减小了亚表面损伤,从而有利于提高陶瓷零件的使用性能。

3 结 论

(1) 基于纵扭超声磨削的切削模型,建立纵扭超声磨削过程中单颗磨粒切削轨迹方程,分析发现:在纵扭超声磨削过程中,由于纵扭超声振动的引入,使得单颗磨粒切削轨迹发生改变,形成高频振动切削分离现象,出现熨压作用,有利于提高加工零件的表面质量。

(2) 基于压痕断裂力学,建立硬脆材料单颗磨粒压痕应力场,进而给出纵扭超声磨削残余应力模型,对纵扭超声磨削残余应力进行仿真计算,分析发现:普通磨削表面残余应力为拉应力,而纵扭超声振动下表面残余应力变为压应力,且表面残余压应力随超声振幅和砂轮转速的增大而增大,随磨削深度和进给速度的增大而减小。

(3) 纵扭超声磨削Si3N4陶瓷表面残余应力的试验结果与理论仿真结果对比发现:两者最大误差为10%,且变化趋势具有高度的吻合性,表明Si3N4陶瓷纵扭超声磨削表面残余应力模型能够预测其加工表面残余应力的变化趋势,可为预测纵扭超声磨削硬脆材料表面残余应力提供参考。

(4) 根据Si3N4陶瓷亚表面微观形貌观测结果发现:普通磨削后,Si3N4陶瓷亚表面出现凹坑和较长的裂纹。而纵扭超声磨削后,Si3N4陶瓷表面出现轻微凹坑,裂纹深度变小。与普通磨削相比,纵扭超声磨削后Si3N4陶瓷亚表面损伤深度最大可降低38%,验证了纵扭超声磨削Si3N4陶瓷后表面残余压应力在一定程度上抑制了微裂纹的产生与扩展,从而提高了零件的使用性能。