改进边界分类的Borderline-SMOTE 过采样方法

马 贺 ,宋 媚,2* ,祝 义

（1.江苏师范大学计算机科学与技术学院，徐州，221116；2.江苏师范大学管理科学与工程研究中心，徐州，221116）

在这个快速发展的信息时代中，每时每刻都在产生大量的数据，随之而来的是数据的不平衡问题，不平衡数据已经成为国内外研究人员关注的研究热点之一.数据的不平衡即多数类样本数量远远超过少数类样本数量，会对分类器的效果造成影响［1］.在欺诈检测［2］、软件缺陷预测［3］、网络入侵检测［4-5］、医疗诊断［6］等领域中存在典型的数据不平衡问题.大多数情况下，数据中的少数类样本是人们关注的焦点，因为少数类的错误分类成本通常远高于多数类.以我国新冠疫情初期为例，核酸检测结果阳性的人数远少于阴性的人数，若将一个阳性病人误诊为阴性，会对疫情管控工作造成重大影响，甚至造成严重后果.此外，部分弱阳性与阴性的症状难以区分，两类样本之间可能存在类重叠状态.因此，需要提高对少数类样本的分类准确率，避免类重叠的错误.

1 相关工作

对于不平衡数据的处理方法有数据级方法和算法级方法.数据级方法致力于对数据进行抽样操作，算法级方法通过调整类别权重缓解不平衡问题.其中数据级方法是最常用的方法，主要有过采样、欠采样、混合采样三种方法.过采样不会造成数据中的信息缺失，表现优于欠采样.过采样方法通过对少数类样本数量的增加来解决不平衡问题，其中最基础的是随机过采样（Random Oversampling）方法.过采样中影响力最大的是Chawla et al［7］的合成少数类过采样技术（Synthetic Minority Oversampling Technique，SMOTE），其寻找少数类样本近邻并在二者之间生成新样本，但其近邻的选择存在盲目性［8］，导致生成样本的随机性.此外，SMOTE 对每个少数类都生成相同数量的合成样本，会使样本边界处的类重叠越来越严重.Han et al［9］针对SMOTE 存在的问题提出两种Borderline-SMOTE 算法，将少数类样本区分为三个区域（Safe，Danger，Noise），主要针对少数类的边界区域样本（Danger）生成新样本，一定程度上缓解了类重叠问题.He et al［10］提出自适应合成过采样方法（Adaptive Synthetic Sampling，ADASYN），考虑少数类附近多数类密度的影响，在密度大的地方生成更多样本，但该方法容易受到离群点的影响.综合上述两种方法，陈海龙等［11］提出一种基于边界自适应合成的少数类过采样方法，在Borderline-SMOTE 的基础上融入自适应的思想和新的插值方式，改善了样本边界模糊的问题，在信用风险预测领域中作用较好，然而，其对不同分布的样本采取不同的插值方式，增大了算法的复杂度.陶佳晴等［12］使用Tomek 链识别类间边界处的少数类样本，以此样本为基础来生成新样本，改变了SMOTE 生成过多样本的缺陷，和Borderline-SMOTE 相比，对边界样本的识别更清晰，但其识别过程需对所有样本点进行距离计算，增大了算法的复杂度.高雷阜等［13］提出一种混合采样方法ICBNMS，通过簇边界负样本移动策略对正负类样本划分，并引入自适应正样本合成技术（ADPST）生成新样本，但ADPST 中存在三个参数，参数的取值对采样效果有一定的影响.Xu et al［14］提出一种基于聚类的过采样方法KNSMOTE，通过聚类选取“安全样本”，对其中的样本进行插值生成新样本，避免对边界样本的生成样本产生边界模糊的影响，但其没有对边界样本进行操作.陈俊丰和郑中团［15］提出一种基于特征加权与聚类融合的方法WKMeans-SMOTE（Weightd Kmeans-SMOTE），通过筛选出聚类一致性系数符合要求的簇边界少数类样本来生成新样本，但其结果易受到聚类个数和噪声的影响，针对其中噪声的影响，Chen et al［16］提出一种针对标签噪声不平衡的自适应鲁棒SMOTE（Self-Adaptive Robust SMOTE，RSMOTE）方法来增强对类边界的分类.

欠采样方法通过减少多数类样本数量来解决不平衡问题，其中最基础的是随机欠采样（Random Undersampling）方法.欠采样中最常使用的是Tomek Link 和ENN（Edited Nearest Neighbours）.前者通过寻找不同类之间互为最近的两个样本构成Tomek Link 对，通过删除其中多数类样本使数据集达到平衡；后者挑选出K个近邻中大部分甚至全部属于少数类样本的多数类样本，剔除这样的样本防止其对分类的影响.

综合过采样和欠采样的混合采样方法，主要思想是先进行新样本的生成，再使用数据清洗手段消除重叠样本，保留“质量好”的样本.Batista et al［17］提出两种结合过采样和数据清洗的混合方法SMOTETomek 和SMOTEENN，既缓解了过采样生成样本造成的类重叠问题，又剔除了多数类样本中的“差质量”的点.Sáez et al[18]提出一种SMOTE和迭代集成噪声滤波器（Iterative-Partitioning Filter，IPF）相结合的方法SMOTE-IPF，来克服不平衡数据集中的噪声和边界问题.

以上研究大都在边界区域生成样本来增强对边界区域的识别，但其对新样本的生成没有一定的约束条件和合理的分配策略，引发类重叠的可能性依然存在，同样会对边界区域造成负面影响.基于以上分析，本文针对在边界区域无约束条件以及合理分配策略进行生成样本的问题，提出一种引入合成因子改进的Borderline-SMOTE 过采样方法，在生成更少样本的情况下增强对边界样本的分类能力.在10 个KEEL 公开数据集上，选取八种采样算法与本文方法在K-近邻（K-Nearest Neighbor，KNN）和支持向量机（Support Vector Machine，SVM）分类器上进行了对比实验.

2 基础知识

2.1 Borderline-SMOTE 过采样方法SMOTE过采样方法对所有少数类样本都“一视同仁”，在所有的少数类样本之间进行新样本的合成，这样可能会造成合成样本在多数类区域中的情况，加大了分类的难度.Han et al［9］对上述问题进行改进，提出Borderline-SMOTE 过采样方法对少数类样本进行划分，将其划分为三个区域（Safe，Danger，Noise），只针对其中属于边缘的少数类样本（Danger）进行合成新的少数类样本（文中所提及的正体Danger 代表边界区域，斜体Danger代表边界样本构成的集合）.

假设T表示整个训练集，pnum和nnum分别表示少数类样本数量和多数类样本数量，P表示少数类样本集合，N表示多数类样本集合.其中，P={P1，P2，…，Ppnum}，N={N1，N2，…，Nnnum}.算法步骤［9］如下.

步骤1.计算样本Pi近邻中多数类样本个数m'.对于少数类样本P中的每一个样本Pi计算其在整个训练集T中的m个近邻，m个近邻中属于多数类样本的个数记为m（'0≤m'≤m）.

步骤2.根据m'的取值来判断样本Pi的所属分类.

（1）当m'=m时，即Pi的m个近邻全都是多数类样本，则Pi属于Noise 区域且不参与下述步骤.

（2）当m/2 ≤m'＜m时，即Pi的多数类近邻数量大于少数类近邻数量，则Pi是易分类错误样本，并且属于Danger 区域.

（3）当0 ≤m'＜m/2 时，即Pi的少数类近邻数量大于多数类近邻数量，则Pi属于Safe 区域且不参与下述步骤.

步骤3.对边界样本求近邻.由步骤2 可知Danger 区域中的样本是少数类样本中的边界样本，因此Danger 区域中的样本属于少数类样本，即Danger⊆P，设Danger=0 ≤dnum≤pnum，dnum表示Danger 区域中的样本数量，对于Danger 区域中的每个样本Pi'计算在少数类P中的k个近邻.

步骤4.生成新样本.根据Danger 区域中少数类样本生成s×dnum个合成样本，s是1～k的整数.对于每个Pi'，从其在P中的k个近邻中随机选择s个近邻.首先计算Pi'与s个近邻二者之间的差difj(j=1，2，…，s)，然后将difj乘以随机数rj∈[0，1)，最后在Pi'和s个近邻之间合成新样本syn，如式（1）所示.

步骤5.对于Danger 区域中的每个都进行步骤4 的操作，可以得到s×dnum个合成样本.

Borderline-SMOTE 算法是在SMOTE 算法的基础上进行改进的，其主要针对边界样本合成新样本，改善了SMOTE 算法生成过多样本产生重叠的问题.

2.2 改进边界分类的Borderline-SMOTE 过采样方法由于Borderline-SMOTE 方法中没有一定的约束条件和合理的分配策略来控制新样本的生成［19］，则生成样本仍会存在类重叠问题.本文在Borderline-SMOTE 过采样方法的基础上引入了合成因子，提出一种改进的Borderline-SMOTE过采样方法，根据数据集中多数类样本、少数类样本、边界样本的数量计算合成因子，进而限制生成样本的数量以及有目的性地选取近邻，使得在生成更少样本的情况下对边界区域样本能实现更好的分类.

该采样方法主要由五个步骤组成，具体过程如下所示.

步骤1.首先对数据集中的少数类样本进行划分，得到边界区域Danger.计算Danger 区域中的样本数量，用dnum表示，初始化每个样本需要生成的样本数量γ=1.

步骤2.计算边界样本的合成因子δ=(nnum-pnum)/dnum.

步骤3.根据δ的取值更新每个样本需要生成的样本数量γ.

（1）当δ＜1 时，从Danger 区域中随机选取δ×dnum个样本放进集合R中.

（2）如若不然，令R=Danger，并根据式（2）更新其中每个样本需要生成的样本数量γ：

步骤4.对于R中每个样本xi，首先计算其在少数类样本P中的k个近邻；其次计算k个近邻对于样本xi的欧氏距离，挑选top-Z个近邻.此处，top-Z=min(γ，k)，即当γ＜k时，选择距离最短的前γ个近邻分别和xi合成新样本，否则选择k个近邻进行合成新样本.

步骤5.假设在步骤4 中选择的近邻记为xk，按照式（3）生成合成的新样本：

其中，random(0，1)表示0～1 的随机数.将返回的所有新生成样本xnew与初始少数类样本P合并后得到平衡之后的样本数据集S.

该方法对边界区域引入合成因子，根据合成因子来进行新样本生成过程中近邻样本的挑选，和Borderline-SMOTE 方法相比，可以生成更少的合成样本，且对边界区域的样本划分更清晰.

3 实验

为了证明本文提出的改进边界分类的Borderline-SMOTE 过采样方法的可行性，与SMOTE［7］，Borderline-SMOTE1［9］，Borderline-SMOTE2［9］，ADASYN［10］，SMOTETomek［17］，SMOTE-IPF［18］，RSMOTE［16］，BA-SMOTE［11］八种经典采样方法分别在二维合成数据集和公开不平衡数据集上进行对比实验，并在公开数据集上进行评价指标的对比.其中，SMOTE，ADASYN，SMOTETomek 三种方法较经典，但没有考虑边界问题，而Borderline-SMOTE1，Borderline-SMOTE2，SMOTE-IPF，RSMOTE，BA-SMOTE五种方法则针对不平衡问题中的边界问题进行了改进.

3.1 评价指标传统的方法是选择准确率（Accuracy，Acc）来评估对数据分类的效果，但在不平衡分类问题中，Acc作为评价指标不是最合理的，因为会发生少数类被误分为多数类的情况.针对不平衡数据，本文选取F1，G-mean 以及AUC作为评价指标，F1 和G-mean 均根据混淆矩阵（见表1）计算.

根据混淆矩阵，可以计算精确率Precision、召回率Recall、特异度Specificity、F1 和G-mean：

其中，F1 衡量分类器对少数类样本的分类精确度，F1 越高代表算法对少数类样本的识别能力越好；G-mean 是兼顾了多数类准确率与少数类准确率的综合指标，是召回率和特异度二者的平均，G-mean 越大越好；AUC表示ROC 曲线下方的面积，AUC越大表示分类的综合效果越好.

3.2 实验设置实验基于Python3.9 和PyCharm来实现，按照7∶3 的比例将数据集划分为训练集和测试集.为了消除实验结果的随机性，对每一个数据集进行五折交叉验证，实验结果取五次实验结果的平均值.为了保证所有方法实验的一致性，所有生成样本的操作中，使用近邻参数K的采样方法均设置为默认参数5，分类器选取K-近邻和支持向量机.此外，为了与Han et al［9］中的两种方法保持同一实验环境，本文方法中涉及的近邻参数M设置为10，与Han et al［9］的默认参数保持一致，因为M的选择会影响到边界样本的确定，进而影响δ的变化.

本文方法中合成因子δ的变化受到两方面的影响，分别是多数类与少数类样本之间的样本数量差nnum-pnum（不平衡数量差）以及边界样本数量dnum，图1 展示了合成因子δ在两个因素共同影响下的变化情况.由图可见，在边界样本数量较多时，边界样本分类较清晰，所需合成的样本数较少.反之，在边界样本数较少时，需要生成更多的样本来加强边界分类，δ会变大.

图1 受不平衡数量差和边界样本数影响的δ 值变化图Fig.1 Plot of variation of δ value affected by imbalanced quantity difference and boundary sample number

3.3 二维合成数据集结果为了直观地显示九种不同采样方法生成样本的情况，选取在Chen et al［16］和Douzas et al［20］中使用的二维合成数据集toy，circles，moons 进行实验.其中，toy 数据集中多数类样本、少数类样本的个数分别为59 和20，总样本个数为79；circles 和moons 数据集使用Python 中的scikit-learn 库进行生成，噪声因子为0.2，两个数据集中的多数类样本、少数类样本的个数均为650 和200，总样本个数均为850.在三个数据集中使用不同采样方法的实验结果如图2～4 所示.

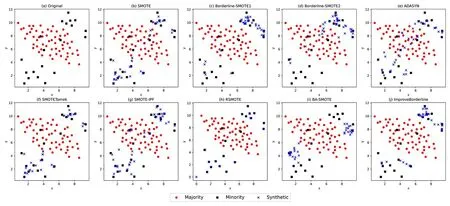
图2 不同采样方法在toy 数据集上采样后数据分布情况Fig.2 Data distribution after sampling on toy dataset by different sampling methods

图2a，3a 和4a 显示了每个二维合成数据集的初始分布.从图2b，3b 和4b 可以看出，SMOTE采样方法对所有的少数类样本都进行合成样本的生成，因此，对属于噪声的少数类样本会生成更多的噪声样本.图2c，3c 和4c 中的Borderline-SMOTE1 采样方法以及图2d 中的Bordrline-SMOTE2 采样方法主要针对少数类的边界样本进行生成新样本，和SMOTE 采样方法相比，加强了对边界的识别效果，但图3d 和图4d 中的Borderline-SMOTE2 采样方法生成的新样本存在与多数类重叠的情况，会对边界的识别造成干扰.图3e 和图4e 中的ADASYN 采样方法在多数类密度较大的少数类样本周围进行生成新样本，图2e 中生成的样本存在一些偏差，同样出现类重叠的问题.图2f，3f 和4f 中的SMOTETomek 采样方法在SMOTE 的基础上增添了欠采样，消除了一部分多数类样本，但和SMOTE 采样方法一样，生成过多合成样本的问题仍然存在.图3g 和图4g 中的SMOTE-IPF 采样方法采用滤波器进行过滤样本，但仍生成了过多的样本，其依赖于滤波器的参数调节，且图2g 中同样出现类重叠问题.图2h，3h 和4h 中的RSMOTE 采样方法生成的样本大都与原有少数类样本过于贴近，缺乏多样性.对比图2h 和图2j 中生成样本的数量，由于该二维合成数据集数据量较少，虽然本文提出的方法生成的样本数没有比图2h 更少，但本文提出的方法生成的样本更具有多样性.图3i 和图4i 中的BA-SMOTE 采样方法同样对边界样本进行处理，但仍会出现一定程度上的重叠区域.本文提出的采样方法在图2j，3j 和4j 中通过在边界区域中引入合成因子来控制生成样本的位置与数量，使得对类间边界的识别更清晰，和其他采样方法相比，生成的合成样本更少，但并不存在其余采样方法存在明显的生成样本跨越多数类样本的问题.以图2c，2d 和2j 为例，与图2c 和图2d 两幅子图相比，引入合成因子的图2j 对近邻的选择进行一定的约束，在一定程度上避免了噪声的产生.

图3 不同采样方法在circles 数据集上采样后数据分布情况Fig.3 Data distribution after sampling on circles dataset by different sampling methods

图4 不同采样方法在moons 数据集上采样后数据分布情况Fig.4 Data distribution after sampling on moons dataset by different sampling methods

3.4 公开数据集结果为验证本文IBSM 方法的有效性，使用来自KEEL 公开数据库的10 组不平衡数据集进行实验，数据集的详细信息如表2所示.

表2 公开数据集信息Table 2 Information on public datasets

表3～5 分别记录了八种经典采样方法和IBSM 方法在使用两个分类器之后获得的F1，G-mean 和AUC，表中黑体字表示最优的实验结果.为了书写简便，将SMOTE［7］，Borderline-SMOTE1［9］，Borderline-SMOTE2［9］，ADASYN［10］，SMOTETomek［17］，SMOTE-IPF［18］，RSMOTE［16］，BA-SMOTE［11］分别简写为SMO，BS1，BS2，ADA，ST，IPF，RS，BA.

表3 IBSM 和八种对比方法在10 个KEEL 数据集上的F1 对比Table 3 F1 of IBSM and other eight methods on 10 KEEL datasets

表5 IBSM 和八种对比方法在10 个KEEL 数据集上的AUC 对比Table 5 AUC of IBSM and other eight methods on 10 KEEL datasets

由表可见，使用KNN 作为分类器时，本文的IBSM 方法和其余八种采样方法相比，在八个数据集上取得最高的F1，在五个数据集上取得了最高的G-mean，在五个数据集上取得最高的AUC.在使用SVM 作为分类器时，IBSM 和其余八种采样方法相比，在九个数据集上取得最高的F1，在三个数据集上取得最高的G-mean，在四个数据集上取得最高的AUC.证明本文提出的采样方法，使F1 得到了较好的提升，即提高了分类器对于少数类样本的识别能力.但该方法在一些数据集上的表现略逊于其余采样方法，这是由于各种数据集的复杂分布，每种方法都不能适用于所有数据集，这与Chen et al［16］的实验结果说明一致.

对于跨越多个数据集并使用多种方法进行的对比实验，为了进一步比较本文方法与其余方法的性能差异，对实验结果进行显著性统计检验.以IBSM 方法作为主控方法，与其余八种采样方法进行Friedman 检验［21］，计算各个采样方法在评价指标上的平均秩（秩越低代表算法性能越高），该方法也被其他研究学者广泛使用［16，20，22］.表6 展示了使用KNN 和SVM 分类器的九种方法的Friedman 排名，表中黑体字表示最优的实验结果.由表可知，本文IBSM 方法的F1 和AUC的排名，不管是使用KNN 还是SVM 分类器，都获得最高的Friedman 排名；使用KNN 分类器时，Gmean 的Friedman 排名最高，使用SVM 分类器时，G-mean 的Friedman 排名为次优.

表6 IBSM 和八种对比方法的Friedman 排名对比Table 6 Friedman rankings of IBSM and other eight methods

4 结论

针对数据不平衡问题提出一种改进的Borderline-SMOTE 过采样方法，从类边界样本的识别出发，通过对边界少数类样本引入生成因子来控制其生成的样本数量.所提方法提高了Borderline-SMOTE 算法于边界生成样本的“质量”，使边界样本能更容易地进行分类，避免如SMOTE 算法一样生成过多样本，且在一定程度上避免了类重叠问题.通过与几种经典的采样方法进行实验对比，证明提出的采样方法在分类器识别少数类样本方面有一定提升.核密度估计在不平衡数据研究中已被证实有效，下一步将研究在边界区域将核密度估计融入采样方法来提升不平衡数据的分类能力以及在不依赖近邻的情况下进行新样本的生成.