利用粗图训练图神经网络实现网络对齐

钱 峰 ,张 蕾 ,赵 姝 ,陈 洁

（1.铜陵学院数学与计算机学院，铜陵，244061；2.安徽大学计算机科学与技术学院，合肥，230601）

图（网络）是一种常用的数据结构，可用来建模不同实体之间的关系，图数据分析中，研究人员运用各种技术（如网络表示学习和深度学习）和手段（如社区发现、节点分类和链接预测）来挖掘图中隐藏的信息.其中，网络对齐（Network Alignment）是一项重要的数据挖掘技术，能发现不同网络中实体之间的等价关系和相似性［1］，在社交网络分析、生物信息学和知识图谱构建等领域得到了广泛应用.例如，在社交网络分析中，可基于用户对齐结果进行跨平台的信息传递［2］；在生物信息学中，对齐不同物种间的蛋白质分子网络可以实现蛋白质功能注释［3］；在知识图谱的构建过程中，利用实体对齐可以完成知识补全［4］.

网络对齐任务中，可利用网络的拓扑结构或节点属性信息来识别不同网络中的相似节点［5］，但由于网络结构的复杂性，传统的网络对齐方法无法满足当下网络对齐任务的需求.近年来，研究人员提出许多基于嵌入的网络对齐方法，包括基于网络嵌入的方法［6-8］和基于图神经网络的方法［9-14］，已有研究表明，基于嵌入方法的性能普遍优于传统方法.网络嵌入（Network Embedding）是一种降维技术，可以将网络节点特征映射到低维向量空间，能更好地表示节点之间的关系［15］.图神经网络（Graph Neural Networks，GNN）是一种深度学习模型，能捕捉节点和边之间的复杂交互关系以及全局拓扑信息.这些技术被广泛应用于各种任务，如节点分类、链接预测和图分类［16］.

图1 展示了基于嵌入的网络对齐过程，其中源网络和目标网络代表不同的网络.假设已知节点1 和节点a是等效节点，即它们指向现实中同一实体，称(1，a)为锚节点对或锚链.网络对齐任务的主要目标是发现源网络和目标网络中更多未知的锚节点对.基于嵌入的网络对齐方法的基本思想是采用嵌入技术来学习不同网络中节点的嵌入向量表示并将它们映射到同一向量空间中，之后通过计算向量之间的距离或相似度来构建对齐矩阵，以发现不同网络中节点之间的对应关系.

图1 基于嵌入的网络对齐过程Fig.1 Example of embedding-based network alignment process

基于网络嵌入的方法通常使用DeepWalk［17］，LINE［18］等算法来学习源网络和目标网络的节点嵌入向量，然而，由于嵌入空间是独立构造的，无法直接利用这些向量表示来计算对齐矩阵.为了解决这个问题，常用的方法是对嵌入矩阵进行线性变换或使用神经网络学习两个嵌入空间的映射关系，但将不同的嵌入空间映射到同一向量空间通常需要大量监督样本，计算成本高，应用过程中存在困难.这些困难主要源于两方面：一是监督样本的获取困难；二是不同网络之间存在结构和语义差异，早期的网络嵌入技术难以捕获节点深层的语义特征.结构差异指两个网络的节点数量不同，语义差异指等效节点的邻域结构不同.

近年来，GNN 已被广泛应用于网络对齐任务.首先，GNN 具有强大的泛化能力，适用于不同拓扑结构的网络；其次，GNN 能捕捉图中节点之间的复杂关系，更好地理解正在对齐的网络的底层结构；此外，GNN 中用来更新节点特征向量的权重参数可以共享，避免空间映射过程，大大降低了对齐问题的复杂性.这些优势使GNN 成为目前解决网络对齐问题的强大工具.

虽然GNN 在网络对齐方面有很大潜力，但仍然存在许多挑战.首先，过拟合是一个普遍存在的问题，导致GNN 的性能下降，这可能由多种因素引起，如模型复杂度、训练次数和参数量等.为了避免过拟合，可以简化模型结构，但这样会降低GNN 学习节点底层特征的能力，影响模型的泛化能力.鲁棒性是另一个问题.GNN 依赖图结构，图中的微小变化可能导致模型输出的显著变化，然而，在网络数据中，噪声和结构缺失不可避免，会影响模型输出的节点表示的质量.最后，可扩展性也是一个需要考虑的问题.GNN 计算成本高，难以扩展到大型网络.此外，在许多应用中，图中的所有嵌入必须定期重新计算.这些因素限制了GNN 在现实场景中的适用性.

为了解决上述问题，提出一种快速鲁棒无监督网络对齐方法（Fast and Robust，FAROS），利用在粗图上训练的GNN 模型来解决网络对齐问题.使用粗图可以更容易地训练GNN，并且内存需求更低.另外，粗图还可以提取网络中的重要节点和边，降低噪声数据对GNN 训练的影响，有助于GNN 学习更具鲁棒性的嵌入向量.FAROS算法包括几个步骤：首先，构造粗图，即保留原始网络主干结构的简化网络；然后，在粗图上训练GNN；最后，利用训练后的GNN 预测两个网络中节点之间的对应关系.本文的主要贡献如下.

（1）提出一种利用粗图训练的GNN 模型来解决网络对齐问题的方法，通过在粗图上训练GNN 模型来提高算法的运行效率和鲁棒性.

（2）为了满足网络对齐任务的需求，采用多种策略来保证训练结果的可靠性，包括参数共享、多阶嵌入和基于伪锚链的自监督学习.这些策略的结合确保了对齐结果的准确性.

（3）在四个真实数据集上的实验结果表明，使用粗图训练的GNN 所需的计算资源更少，能显著提高算法的运行效率和鲁棒性.此外，采用的训练方法也能保证算法的对齐精度.

1 相关工作

1.1 图粗化技术图粗化（Graph Coarsening）是一种在保留原始图的关键特征的情形下显著减少图规模的技术.使用图粗化算法可以生成一个更简单的粗图，它具有更少的节点和边，所以对该图的分析和处理会更容易.图粗化的方法有很多种，包括基于匹配的方法、基于聚类的方法和基于谱的方法.

1.1.1 基于匹配的方法基于匹配的方法是一种有效的图粗化方法，其主要思想是使用匹配规则来寻找相互匹配的节点，并通过互匹配的节点来构造超级节点.这一操作可以重复进行，直到没有节点能匹配或达到所需的粗化水平.通常可以根据图的固有特征制定相应的匹配规则，例如节点的度或节点共邻的数量.代表算法有重边匹配（Heavy Edge Matching，HEM）算法［19］、结构等价匹配（Structural Equivalence Matching，SEM）算法［20］和归一化重边匹配（Normalized Heavy Edge Matching，NHEM）算法［21］.其中，HEM 算法采用贪心原则，依据边的权重来匹配合并相邻节点；SEM 算法将具有相同结构的节点视为等价节点进行匹配；NHEM 算法在HEM 的基础上进行改进，通过对每个节点的边权重进行归一化处理使所有边权值的和为1，避免权重过大或过小而导致的匹配偏差.

1.1.2 基于聚类的方法基于聚类的方法采用图聚类或社团检测算法，按照特定标准（如距离或模块度）将节点划分为不同的簇，使同一簇内节点的相似性尽可能大，同时，不同簇的节点差异性也尽可能大，然后递归地合并这些簇，直至达到所需的粗化水平.代表的图聚类算法有K-means［22］和高斯混合模型（Gaussian Mixture Model，GMM）［23］等.K-means 是一种迭代求解的聚类分析算法，GMM 是一种基于概率模型的聚类方法，代表的社团检测算法有鲁汶（Louvain）算法［24］等.

1.1.3 基于谱的方法基于谱的图粗化方法的目的是保留原始图和粗图之间的谱特性.图中的谱通常指拉普拉斯（Laplacian）矩阵，用于在谱域上描述图结构和节点之间的关系.Loukas［25］提出一种基于受限谱逼近的多层次图粗化算法，可以在保持原始图结构特征不变的情况下将其缩减为更小规模的图.受限谱逼近是一种谱逼近方法，其主要思想是选择一个低维子空间，使得在该子空间中，原始图和粗图之间的谱距离最小化.

1.2 基于嵌入的网络对齐基于嵌入的网络对齐是一种通过结合不同的嵌入技术解决网络对齐问题的方法，可以分为两类，即基于网络嵌入的方法和基于图神经网络的方法.

1.2.1 基于网络嵌入的方法基于网络嵌入的方法使用DeepWalk［17］或LINE［18］等网络嵌入技术来学习不同网络中的节点表示.Man et al［6］提出PALE（Predicting Anchor Links via Embedding）算法，利用观测到的锚链为监督信息，结合LINE来捕捉不同网络之间的结构规律和相似性，并使用学习的嵌入向量来预测锚链.其中，锚链被视为网络中的关键节点，它们的位置和连接关系被用来指导嵌入向量的学习，通过这种方式PALE算法能更好地捕捉网络的结构和特征，提高预测的准确性和可靠性.Heimann et al［7］提出REGAL（Representation Based Graph Alignment）算法，通过扩展低秩矩阵近似的Nyström 方法［26］和设置标准节点来加速表示学习，并通过Kd-tree 方法［27］实现贪婪对齐.Nguyen et al［8］提出NAWAL（Network Alignment with Self-supervised Anchor Links）算法.首先，分别学习源网络和目标网络的节点向量表示；然后，使用生成对抗网络（Generative Adversarial Networks，GAN）［28］在无监督样本的情况下学习一个映射函数W，将两个网络的嵌入空间协调到一个公共空间中，在这个过程中，通过生成的伪锚链，利用Procrustes 的封闭解［29］进一步优化嵌入；最后，采用贪婪启发式的方法进行对齐.Zhu et al［30］提出CAPER（Coarsen，Align，Project，Refine）算法，首先将输入网络粗化为不同粒度的网络，接着在最粗的网络上使用现有对齐算法（如REGAL）获得最粗的对齐矩阵，最后，将对齐结果进行逐层映射，最终得到最细层次的对齐矩阵.此外，CAPER 在映射过程中，通过在不同粒度的对齐矩阵上使用CONE_Align［31］来改善对齐结果.CONE_Align 提供了一种基于近邻一致性（Neighborhood Consistency）的优化方法来提高现有网络对齐算法的鲁棒性.具体地，如果已对齐的节点对具有相似的特征，则它们的邻居节点中很可能也存在相互对齐的节点.

1.2.2 基于图神经网络的方法基于图神经网络的方法是利用图神经网络模型，例如图卷积网络（Graph Convolutional Network，GCN）［32］和图同构网络（Graph Isomorphic Network，GIN）［33］来学习不同网络中节点的表示，并通过学习到的特征向量推断不同网络中节点之间的相似性.Trung et al［9］提出GAlign 算法，利用GCN 学习节点的多阶嵌入.为了提高模型性能，GAlign 设计了一种数据增强方法，主要通过对网络节点的边进行随机添加或删除操作来增加模型的鲁棒性和泛化能力，为网络对齐提供高质量的节点嵌入表示.Qin et al［10］提出G-CREWE（Graph CompREssion with Embedding）算法，首先，利用GCN 提取节点特征，获得原始网络的对齐结果；然后使用提出 的 MERGE（Minimum DEgRee NeiGhbors ComprEssion）方法对网络进行压缩，并在粗图上进行对齐；最后，将来自两种粒度网络的对齐结果合并，以实现高质量的对齐性能.Gao et al［11］提出WAlign 算法，利用LGCN（Lightweight GCN）模型来捕获网络的局部和全局结构信息，获得高质量的节点特征向量，然后通过Wasserstein 距离［34］鉴别器生成伪锚节点对，并在统一的优化框架下，利用对抗训练的方法迭代更新嵌入和鉴别器参数来提高对齐准确率.Park et al［12］提出Grade-Align算法，首先使用GIN 生成嵌入向量并构建嵌入相似度矩阵，然后通过迭代的方式，融合嵌入相似度矩阵和不断更新的Tversky 相似度矩阵来生成伪锚节点集合，逐步提高算法的对齐准确性.Tversky 相似度［35］是一种基于集合的相似度计算方法，用于评估两个集合之间的相似程度.构造Tversky 相似度矩阵的方法如下：首先，构建两个新图；接着，依据伪锚节点集合，将来自另一方的节点和相应的边加入到各自的图中；最后，计算不同图中两个节点邻域集合之间的Tversky 系数，构造Tversky 相似度矩阵.Lu et al［13］提出Bi_GANA（Bi-layer Graph Attention Neural Network for Network Alignment）算法，利用双层图注意力神经网络对多维用户特征和社交网络的局部和全局拓扑信息进行建模，通过不规则图和多维用户特征信息实现社交网络用户对齐问题.Huynh et al［14］提出NAME（Network Alignment with Multiple Embedding）算法，集成多种嵌入技术以创建更丰富、更准确的节点表示，并通过端到端的学习来实现高效对齐.

尽管GNN 在网络对齐领域已取得了巨大的成功，但仍然存在一些缺陷.在处理大规模图数据时，GNN 模型需要大量的计算和存储，限制了模型的规模和性能.同时，噪声数据会干扰GNN的学习过程，使模型无法准确地捕捉节点之间的关系和特征.为了解决这个问题，GNN 模型可以使用数据增强技术来增加训练数据的数量，但数据增强也会增加噪声数据的数量，进一步干扰模型的训练.

针对这些问题，本文提出一种基于图神经网络的无监督网络对齐方法.与上述方法不同，该方法使用粗图训练GNN 模型来加快训练速度、减少内存需求，并提高其应对噪声数据的能力.在粗图上训练GNN，可以使GNN 在更小的数据集上训练，有效减少了模型参数，提高了训练效率.此外，粗图可以识别网络中的重要节点和边，为网络对齐提供更准确的信息，缓解因噪声数据给GNN 模型训练带来的不稳定性和误差.

2 问题定义

本文的研究对象为两个属性网络.通常，一个无向的属性网络可表示为G=(V，E，A，X).其中，集合V记录节点的索引信息.集合E记录边的信息，E⊆{{u，v}⊆V|u≠v}.矩阵A∈RN×N为邻接矩阵，N=|V|，描述节点之间的连接关系.若 (u，v)∈E，则A[u][v]=A[v][u]=1，反之，A[u][v]=A[v][u]=0.连接关系也可以用链接矩阵E∈R2×|E|表示，其中，第一个列表是所有边上起始节点的索引，第二个列表是对应边上目标节点的索引.矩阵X∈RN×f是属性矩阵，记录每个节点的初始特征向量，f为向量的维度.

网络对齐任务的目标是发现源网络和目标网络中的锚节点对.其中，锚节点对表示为：

输入为源网络Gs=(Vs，Es，As，Xs)和目标网络Gt=(Vt，Et，At，Xt).

3 FAROS 算法

FAROS 算法的框架如图2 所示，分训练和推理两个阶段.在训练阶段，首先对两个网络进行粗化，然后在粗图上训练GNN 模型参数.在推理阶段，将源网络和目标网络输入训练好的GNN模型，通过前向传播推断原始网络的节点向量表示并计算最终的相似矩阵.为了提高表示质量，FAROS 引入基于伪锚节点对的自监督学习.具体地，通过首轮训练得到的多阶节点嵌入计算来对齐矩阵并采集伪锚节点对集合，然后传递给GNN 模型用于下一轮的训练并获取新的对齐矩阵.本节首先介绍粗图的构造方法，然后介绍采用的GNN 模型架构和训练方法，最后给出FAROS 算法的描述.

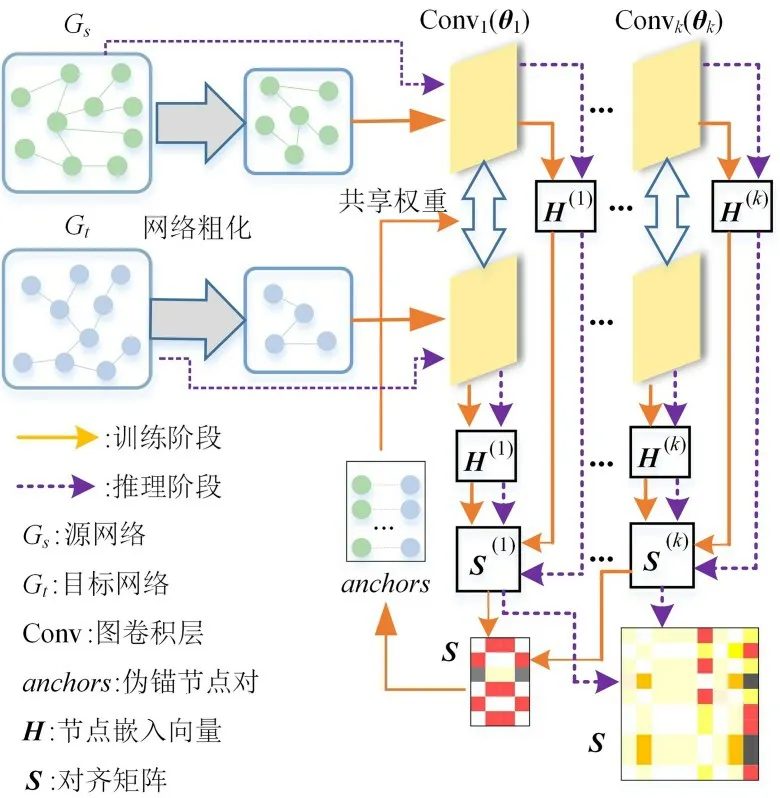
图2 FAROS 算法的框架图Fig.2 The overall framework of FAROS

3.1 网络粗化训练GNN 模型是一个昂贵的过程，尤其是在处理大型网络时.为了减少训练开销，本文采用粗图训练GNN 模型，这样做主要有两个优点：第一，有效减少需要优化的参数的数量；第二，提取网络中最重要的主干结构，从而将训练过程集中在网络最重要的特征方面.因此，该方法不仅能提高模型的训练效率，还可以提高模型的鲁棒性.

由于结构噪声对图拉普拉斯矩阵的谱影响较小［36］，因此本文采用基于谱的粗化方法来简化网络结构.具体地，采用Loukas［25］的基于邻域的局部变化的图粗化方法，利用受限谱逼近方法来缩减图的大小，在不显著改变图的基本属性的情况下，具有很强的谱和割保证.因此，该方法可以有效地简化网络结构，同时保留原始图的关键谱（结构）特性.另外，该方法还提供参数r来控制输出粗图的规模，r=1-n/N，其中，N是原始图的节点数，n是粗图的节点数.算法的输出为粗图的邻接矩阵和分配矩阵M∈RN×n，分配矩阵决定哪些邻居可以聚在一起形成超节点.根据分配矩阵可获得粗图的属性矩阵，计算如下：

算法1 描述了网络结构粗化的过程，通过搜索连通子图并设置相应的阈值来减少数据噪声的影响，进一步过滤网络中的噪声数据.其中，下标*表示源网络和目标网络的s或t.

算法1 的时间复杂度主要由处理子图的循环和处理特征的循环决定.假设有l个子图，每个子图的节点数为m，则处理子图的循环的时间复杂度为O(lm2)，处理特征的循环的时间复杂度为O(lm).因此，算法1 的时间复杂度为O(lm2).

3.2 模型训练网络对齐中，通过GNN 学习节点的特征向量来构建对齐矩阵.一个标准的GNN 模型［37］由k个图卷积层组成，每个图卷积层通过消息传递策略来捕获网络的结构和属性信息［38］.从初始的特征开始，第k层的节点特征由第k-1 层的相邻节点的特征聚合而成.具体地，设源网络或目标网络中的节点v在第k-1 层的特征向量为，那么，第k层的图卷积可表示为：

其中，下标*表示源网络和目标网络的s或t，σ()是激活函数，N(v)是节点v的邻居节点集合，是第k层的需要学习的模型参数.

为了确保源网络和目标网络中的节点特征表示在相同的向量空间中，采用了权重共享机制，即使用相同的参数来更新每个节点的特征向量.此外，还采用多阶嵌入的方法［9］，可以更好地利用网络的局部和全局拓扑信息来增强模型的语义表示能力.

对齐矩阵S的计算如下：

尽管GNN 可以捕捉网络之间的复杂关系，提高网络对齐算法的效率和精度，但其性能优势通常需要结合特定的任务设计模型架构并提供足够的监督样本才能体现.为了帮助GNN 更好地识别两个网络中的节点之间的对应关系，利用自动生成的伪锚节点对集合，以迭代的方式训练GNN 模型，提高最终对齐的准确率.

具体地，在首轮训练过程结束后，根据式（3）得到对齐矩阵，从中采集不同网络中节点之间的相似度，将结果以三元组(i，j，Sij)的形式保存到候选列表中并进行降序排序，其中，节点i是源网络的节点，节点j是目标网络的节点，Sij是其对应的相似度.接着，依序选择相似度最高的节点对加入伪锚节点对集合，并从候选列表中删除已加入伪锚节点对集合的节点的所有数据.最终，将得到的伪锚节点对集合传递给GNN 模型用于下一轮训练.

在每一轮训练中，GNN 模型都计算对齐矩阵并生成新的伪锚节点对集合，以帮助改善后续的表示学习过程.需要注意的是，本研究采用了一个渐进式采集策略，即逐步增加锚节点对的采集数量，能更好地控制训练的复杂性和效率.

模型训练的目标函数由两部分组成，分别是：

式（4）的目标函数用于计算预测的链接矩阵与实际的链接矩阵之间的误差.其中，用于聚合节点嵌入的矩阵不是固定的，目的是最小化相同卷积层节点嵌入的距离，同时最大化不同卷积层嵌入之间的距离，从而能更精确地捕获一阶和高阶邻域结构.

其中，P是伪锚节点对集合.

式（5）的目标函数是让每层的伪锚节点对的嵌入在表示空间中趋于相似，因为真实的锚节点对应有相似的嵌入.换言之，通过调整嵌入向量，使同一组锚节点在不同的层中的嵌入具有相似性，从而提升最终对齐结果的准确性和可靠性.

3.3 算法描述FAROS 的具体描述如下.

算法2 中，GNN 前向传播的时间复杂度为O(|A*|)，反向传播的时间复杂度为O(|H*|2).设n是粗图的节点数，获取伪锚节点的时间复杂度为O(n3+n2+nlgn)=O(n3).

4 实验

首先介绍实验采用的数据集、对比算法、评价指标和实验参数设置，然后通过多组实验来验证FAROS 算法的性能.

4.1 数据集使用四个数据集进行实验，每个数据集包含两个来自真实网络的节点、边和节点属性信息文件.

douban 数据集来自豆瓣网，包括douban online/offline［39］，其中节点代表用户.douban online中，边代表用户之间是否互为好友，douban offline中，边代表用户是否参加了同一场线下活动.allmv/imdb 数据集来自Rotten Tomatoes 网站和Imdb 网站，其中节点代表电影，边代表两部电影至少有一位共同演员.flickr，myspace 和lastfm 数据集均来自社交网络平台，其中节点表示用户，边代表用户之间的交互关系.

表1 列出了这些数据集的详细统计信息.

表1 实验使用的数据集的统计信息Table 1 Statistical information of the datasets used in experiments

4.2 对比算法选择五种无监督的网络对齐算法作为对比算法.

REGAL［7］首先将源网络和目标网络组合起来，然后利用隐式矩阵分解方法（xNetMF）进行联合嵌入，得到节点表示向量，最后使用贪婪匹配的方法对齐不同网络间的节点.

GAlign［9］使用GCN 学习两个网络中每个节点的多阶嵌入，然后根据不同卷积层输出的节点表示向量的相似性计算多个对齐矩阵，最终通过融合多个对齐矩阵实现节点对齐.

NAWAL［8］首先利用Node2Vec［39］算法学习节点的特征表示，然后使用自监督锚链接来实时更新节点的嵌入向量，并通过最大化锚链接之间的相似性来实现对齐.

WAlign［11］首先通过LGCN 模型来学习节点的嵌入向量，然后利用一种新颖的Wasserstein 距离鉴别器来识别用于更新节点嵌入的候选节点对，最后通过自监督的对抗学习得到适合对齐任务的嵌入.

Grad-Align［12］使用GIN 学习节点的特征向量，然后融合嵌入向量相似性和节点结构的Tversky 相似性.逐步发现强一致性的节点对，以便更好地捕获跨网络的节点的一致性.

4.3 评价指标和共同参数设置为了评估算法的性能，使用两个度量指标来衡量网络对齐结果的优劣，分别是MAP（Mean Average Precision）［9］和Precision@K［9，11］.具体地：

其中，P*是真实的锚节点对集合，ri是真实的锚目标节点的排名.

其中，()是从目标网络节点集合Vt中选取的一个子集，即对于源网络中的每个节点vs，找出目标网络中与之对应的靶节点，这些靶节点是在S(，·)中具有最高相似度得分的前K个节点.ΙA()是指示函数（Indicator Function），用于判断节点对(，vt)是否属于真实锚点对集合P*，如果属于，其值为1，否则其值为0.

为了确保实验的公正性，选择文献中的默认参数作为对比算法的参数.在初始化共同参数时，FAROS 和对比算法的参数使用相同的数值.其中，嵌入维度d设为128，卷积层数k设为2，中间层维度与嵌入维度相同.使用tanh 激活函数.使用学习率为0.005 的Adam 优化器进行模型优化，并将权重衰减率设为5×10-4.对于FAROS算法，网络压缩率r设为0.7.

实验环境：Windows 10，16 G 内存，Inte（lR）CPU i7-4790 @ 3.60 GHz.编程语言为Python，基于Pytorch 深度学习框架实现GNN 模型.

4.4 对比实验通过实验观察FAROS 和对比方法在网络对齐任务上的性能差异，表2 展示了不同方法在相同实验条件下四个数据集上的MAP和运行时间，表中黑体字表示最优结果，下画线表示次优结果.

表2 FAROS 和对比方法在四个数据集上的MAP 和运行时间的比较Table 2 MAP and running time of FAROS and baselines on the four datasets

由表可见，在四个数据集上的计算效率，REGAL 最优.在基于GNN 的对比方法中，GAlign表现最优.除了douban 数据集，Grad-Align 是最慢的方法，比其他方法多花费几个数量级的时间.NAWAL 和WAlign 都采用基于伪锚链的对抗自监督学习改善最终的节点嵌入，但二者的训练目标不同，前者将不同网络的特征向量空间映射到同一个语义空间，后者使节点嵌入向量之间的Wasserstein 距离最小化，很明显，引入对抗机制增加了算法的运行时间.Grad-Align 通过嵌入相似度和Tversky 相似度来生成强关联的节点对，并采用图增强策略迭代计算Tversky 相似度矩阵，以更精确地识别不同网络间的节点对应关系.然而，该策略不仅对内存空间需求大，还极大地增加了算法的运行时间.FAROS 在计算效率上有明显优势，虽然为了提高网络对齐精度而采用了基于伪锚链的自监督学习，但使用粗图的训练方式弥补了自监督学习给算法效率带来的影响.与GAlign 相比，在douban 数据集上，FAROS的运行时间减少71.58%；在allmv/imdb 数据集上，FAROS 的运行时间减少65.64%；在flickr/myspace 数据集上，FAROS 的运行时间减少80.69%；在flickr/lastfm 数据集上，FAROS 的运行时间减少80.71%.实验结果表明，FAROS 的计算效率十分出色，而且，随着网络规模的增大，这种优势会越来越明显.

对齐性能，不同方法在四个数据集上的MAP存在明显差异.NAWAL 在所有方法中表现最差，几乎是随机对齐，这是由于采用DeepWalk 生成节点的嵌入向量，构造的伪锚链不准确，使对齐结果不理想.基于GNN 的网络对齐方法都表现良好.FAROS 除了在allmv/imdb 数据集上的MAP略低于Grad-Align 外，在其他数据集上都取得了最优结果.实验结果表明，在对齐性能方面，与对比方法相比，FAROS 具备一定的优势.

为了进一步验证FAROS 在网络对齐任务中的性能优势，在相同的实验条件下，使用Precision@K来评估不同方法的性能差异，实验结果如表3～6 所示，表中黑体字表示最优结果，下画线表示次优结果.

表3 douban online/offline 数据集上FAROS 算法与对比算法的Precision@K 对比Table 3 Precision@K of FAROS and baselines on the douban online/offline dataset

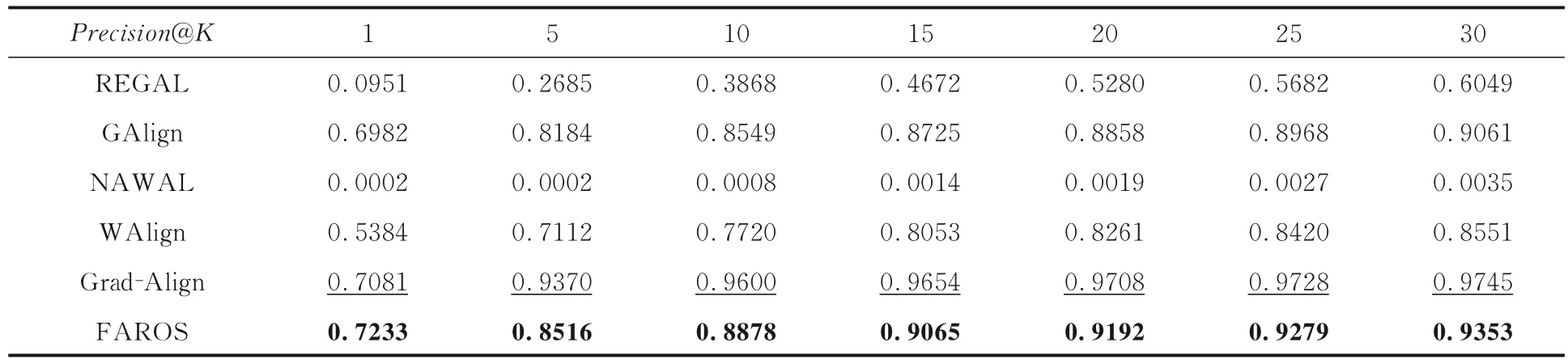
表4 allmv/imdb 数据集上FAROS 算法与对比算法的Precision@K 对比Table 4 Precision@K of FAROS and baselines on the allmv/imdb dataset

表5 flickr/myspace 数据集上FAROS 算法与对比算法的Precision@K 对比Table 5 Precision@K of FAROS and baselines on the flickr/myspace dataset

表6 flickr/lastfm 数据集上FAROS 算法与对比算法的Precision@K 对比Table 6 Precision@K of FAROS and baselines on the flickr/lastfm dataset

由表3～6 可见，在实验条件相同而K不同时，基于图神经网络的GAlign，WAlign 和Grad-Align 算法性能稳定，表现较好.其中，Grad-Align的对齐性能总体上优于其他对比算法.除了allmv/imdb 数据集，FAROS 均表现出最优的性能.以Precision@5 为例，Grad-Align 结果均为次优，与其相比，FAROS 的性能在douban 数据集上提升6.56%，在allmv/imdb数据集上下降9.11%.这是allmv/imdb 的聚类系数过高导致的.网络的聚类系数较高时，节点之间的连接较紧密，网络的局部结构较复杂，粗化后的网络可能会丢失一些重要的局部信息；网络的聚类系数较低时，节点之间的连接较稀疏，网络的局部结构较简单，粗化后的网络可能会保留更多的局部信息.因此，在进行网络粗化时需考虑网络的聚类系数及其他网络特征以获得更好的粗化效果.以Precision@5 为例，与Grad-Align 相比，FAROS 的性能在flickr/myspace 数据集上提升133.92%，在flickr/lastfm数据集上提升23.26%.综合来看，在不同规模的数据集中，FAROS 模型的运行时间和对齐精度都表现出优越的性能.

4.5 性能分析使用粗图训练GNN 可以有效减少需要优化的参数量，提高训练效率，前提是不能使算法精度下降.为了验证这一点，调整参数r，分别对四个数据集中的网络实施不同程度的压缩，观察FAROS 算法的性能变化.实验中保持其他参数不变，将参数r的数值由0 变为0.8，调整步长为0.2，选取Precision@K（简称P@K）作为评估指标，实验结果如表7～10 所示，表中粗体字表示最优结果，下画线表示次优结果.

表7 在douban online/offline 数据集上FAROS 算法在压缩比不同时的P@K 对比Table 7 P@K of FAROS with different compression ratios on douban online/offline dataset

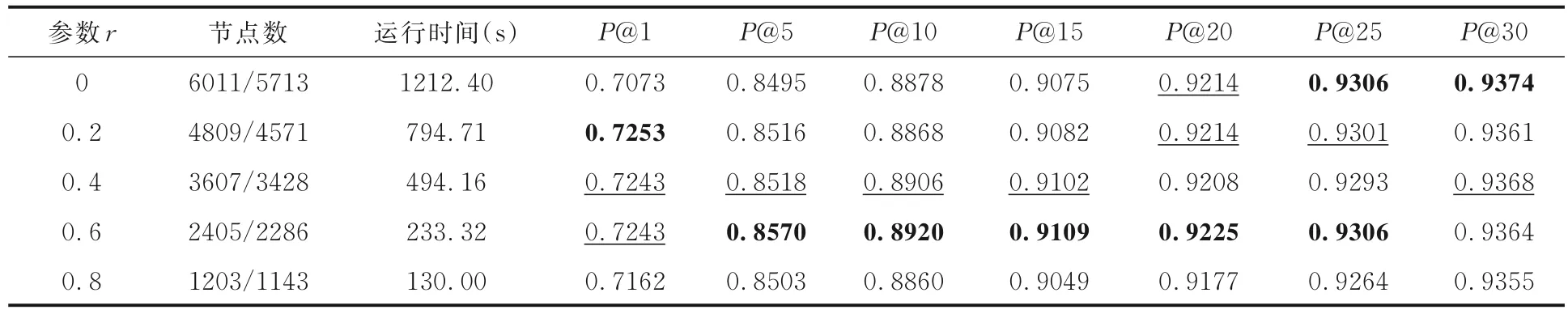
表8 allmv/imdb 数据集上FAROS 算法在压缩比不同时的P@K 对比Table 8 P@K of FAROS with different compression ratios on allmv/imdb dataset

表9 flickr/myspace 数据集上FAROS 算法在压缩比不同时的P@K 对比Table 9 P@K of FAROS with different compression ratios on the flickr/myspace dataset

表10 flickr/lastfm 数据集上FAROS 算法在压缩比不同时的P@K 对比Table 10 P@K of FAROS with different compression ratios on the flickr/lastfm dataset.

由表7～10 可见，在其他参数相同时，随着网络规模的减小，GNN 的训练速度有显著的提高.压缩程度为0.8 时，P@K可能会有所下降，但下降的幅度不大，而且在不同数据集上的下降幅度也不同.比较FAROS 算法在未压缩与压缩的数据集上的运行时间和P@5，参数r=0.6 时，在压缩后的网络中，节点数量约为原始网络的1/6.在douban，allmv/imdb，flickr/myspace 和flickr/lastfm 数据集上，FAROS 算法在未压缩数据集上的运行时间分别是在压缩数据集上的4，5，6，7 倍.同时，P@5 在douban 数据集上增加了0.34%，在allmv/imdb 数据集上增加了0.88%，在flickr/myspace 数据集上减少了14.12%，在flickr/lastfm 数据集上增加了21.61%.由于网络压缩率和准确性之间没有确定的关系，因此FAROS 算法需要对两者作出权衡.但是，当网络规模被适度压缩后，P@K可能会有所提升，这可能是因为GNN 模型具有较强的泛化能力，同时网络的粗化过程有助于减少数据中的噪声，使GNN 的训练过程更加集中在网络的重要特征上.实验结果表明，较大程度的网络压缩不会对算法的性能产生太大的影响，反而可能提高算法的准确性.因此，使用粗粒度的网络训练GNN 可以在一定程度上减少需要优化的模型参数量，同时又不会对算法精度造成太大影响.

对算法的鲁棒性进行验证，通过给网络删除或添加边来模拟结构噪声.一般地，随着噪声的增加，算法的精度会下降.实验中保持其他参数不变，将参数r设置为0.7，并在四个数据集上随机删除或添加固定比例的边，比例分别为0.02，0.04，0.06，0.08，0.1，0.2.使用P@5 作为评估指标，实验结果见图3 和图4.

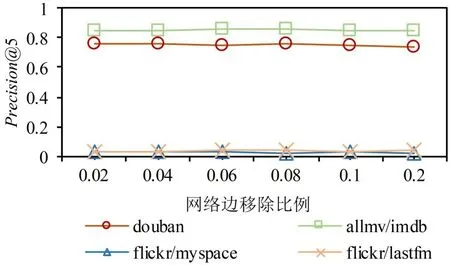
图3 在四个数据集上对FAROS 算法移除不同比例边的P@5 的对比Fig.3 P@5 of FAROS with different ratios of edges removed on four datasets

图4 在四个数据集上对FAROS 算法添加不同比例边的P@5 的对比Fig.4 P@5 of FAROS with different ratios of edges added on four datasets

由图可见，随着噪声幅度的增加，无论是删除还是添加边，P@5 均有微小波动，但没有明显变化.在douban 数据集上，当添加边的比例增至0.2 时，P@5 略微下降，与添加0.02 的边相比，下降率仅为2.1%，证明基于粗图的训练策略可以在一定程度上消除噪声数据对GNN 模型的影响并保持稳定的对齐性能，也证明其具备较强的鲁棒性.综合来看，由于在粗图上训练图神经网络需要的计算资源更少，其能达到与在精细图上训练的图神经网络相似的性能.

4.6 消融实验探究不同的GNN 模型和网络粗化策略对FAROS 性能的影响.首先使用三种常见的卷积图神经网络模型，分别是GCN［32］，GraphSAGE［40］和GIN［33］来替换本文中的GNN 模型.实验结果如图5 所示.

图5 FAROS 使用不同GNN 模型的P@5 对比Fig.5 P@5 of FAROS with different GNN models

由图可见，使用不同的图神经网络训练的嵌入向量进行网络对齐时，FAROS 在不同数据集上的性能表现不同.尽管在总体上，FAROS 采用GNN 模型的网络对齐任务的准确率优于其他图神经网络模型，表现稳定，但这并不意味着该模型比其他模型更适合网络对齐任务.事实上，影响GNN 性能的因素很多，而且图神经网络的训练过程不简单，为了获得最佳性能需要精心调整GNN的学习率、层数和每层神经元的数量以及训练策略的选择.因此，使用GNN 进行网络对齐是一项具有挑战性的任务，需要仔细调整各种参数.

采用三种其他粗化方法替代本文使用的粗化方法（variation_neighborhoods），分别是基于代数多重网格的粗化算法（algebraic_jacobi）［41］，基于重边匹配的粗化算法（heavy_edge）［42］和基于Kron简化的粗化算法（kron）［43］.实验结果如图6 所示.

图6 FAROS 使用不同粗化方法的P@5 对比Fig.6 P@5 of FAROS with different coarsening methods

由图可见，不同的粗化算法对算法的对齐结果的影响较小.总体上，本文采用的粗化策略十分有效，特别是在噪声数据较多的flickr/myspace数据集上，其性能比次优的algebraic_jacobi 方法高28.57%.这可能是因为本文使用的粗化策略能更好地处理噪声数据，还能更准确地捕捉节点之间的语义关系.

5 结论

为了提高GNN 的运行效率并缓解噪声数据对GNN 性能的影响，本文提出一种快速鲁棒的无监督网络对齐方法FAROS，利用GNN 学习不同网络间节点的相似性，并将其用于网络对齐任务.与其他基于GNN 的网络对齐方法相比，FAROS 使用粗图来训练GNN 模型参数，提高了算法的效率和鲁棒性.此外，FAROS 还采用多种策略来实现可靠的训练，以适应网络对齐任务的需求，有效保证了对齐结果的准确性.在基准数据集上进行了广泛实验，证明FAROS 的有效性、效率和鲁棒性都具有优越性.

总体上，FAROS 在保障对齐任务准确性的同时，还具有更高的时间和空间效率，使其能有效部署在一系列现实环境中.然而，由于粗图中可用的训练数据量有限，GNN 超参数的选择通常很困难，仍需进一步提高其在网络对齐任务中的性能.未来可以探索更多的图粗化算法和超参数调整策略，进一步提高GNN 在网络对齐任务中的性能和鲁棒性.