基于深度残差网络的(n,1,m)卷积码盲识别

刘 杰,朱宇轩,马 钰

(1.军事科学院系统工程研究院,北京 100191;2.电磁空间认知与智能控制技术重点实验室,北京 100191)

0 引言

现代数字通信系统中,为保证信息稳定可靠传输,往往在调制前对信息序列采用纠错编码技术,以实现接收端数据的检错纠错。无论是民用领域的认知无线电系统,还是军事领域的非合作信息截获技术,纠错编码盲识别技术正日益发挥着重要作用[1-5]。

(n,1,m)卷积码作为最早被发明的纠错编码技术之一,因编译码技术成熟、纠错能力较强,目前已被广泛应用于电话、卫星和无线信道的数据传输中。针对(n,1,m)卷积码的盲识别问题,目前公开发表文献中所提方法主要存在两方面的不足:一是对误码的容错性较差,比如文献[6]中基于关键模方程得到的Gröbner基约化算法,文献[7]中基于多项式辗转相除得到的欧几里得算法,文献[8-14]中根据接收序列矩阵化简后秩亏和列向量分布得到的矩阵分析法等。在实际环境,特别是非合作条件下,受噪声、干扰和信号预处理误差的影响,解调、解交织以后得到的二元编码序列中往往存在很多误码,从而约束了上述方法的实用性。二是在假定预知很多先验信息的条件下,才能完成部分参数的识别。比如Gröbner基约化算法、欧几里得算法和文献[15-17]提出的沃尔什-哈达玛变换(Walsh-Hadamard Transform,WHT)算法均在码长、编码约束长度、码字起点已知的情况下完成对生成多项式的识别。因此,目前仅有矩阵分析法能较完整的完成(n,1,m)卷积码识别,其他方法或结合矩阵分析法进行预处理,从而限制了整体识别准确性,或从不同起点和长度顺序截取编码序列,经多次迭代完成码长等参数的验证,整个过程比较繁琐。

由以上分析不难发现,(n,1,m)卷积码识别的关键在于码长n、码字起点和存储级数m的识别。针对传统方法存在的不足,本文提出了一种基于残差网络(Residual Network,ResNet)的(n,1,m)卷积码盲识别新方法。首先利用常用的(n,1,m)卷积码在不同误码率下生成编码数据,然后直接按制定长度随机划分,输入ResNet完成监督学习。实验结果验证了所提方法的有效性,无需其他先验信息,即可完成码长、编码约束长度和码字起点的识别,且容错性能明显优于传统方法。

1 问题描述

对于(n,1,m)卷积码,参数n、m分别表示码长和存储级数[18-19]。令s(x)表示卷积码信息序列,C(x)表示编码序列,G(x)表示生成多项式矩阵,则编码方程在环F2(x)上可表示为:

C(x)=s(x)·G(x),

(1)

式中:

(2)

(3)

且

(4)

gi(x)=gi,0+gi,1·x+…+gi,m·xm,i=0,1,…,n-1,

(5)

(6)

设传输时对应误码多项式矩阵为:

(7)

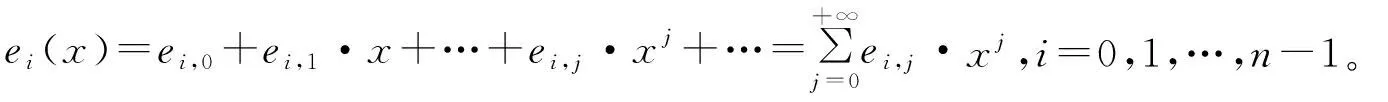
i=0,1,…,n-1。

(8)

为便于分析,将上式转化为二元比特流形式,则:

V=(vk-1,l,vk-1,l+1,…,vk-1,n-1,vk,0,vk,1,vk,2,…,
vk,n-1,vk+1,0,vk+1,1,…,vk+M,p,vk+M,p+1)。

(9)

可以看出,去除编码序列V首尾两组不完整的码字,中间共有M组完整的码字。卷积码盲识别是在仅知道序列V的前提下,通过合适的方法恢复出码长n、码字起点vk,0和存储级数m等参数,进而计算得到生成多项式。

2 基于ResNet的(n,1,m)卷积码识别

2.1 模型结构设计

深度神经网络[20]属于机器学习算法的一个重要分支,目前已被广泛应用于计算机视觉、自然语言处理等领域。本文考虑到卷积编码的数据特征,采用卷积神经网络中的ResNet模型进行训练,其基本组成结构如图1所示,共两种形式,图中3×3表示卷积核大小,64表示输出通道的维数。与普通卷积神经网络相比,ResNet模型将输入直接传到网络输出,使得学习目标变成了期望输出与输入的差值,进而避免了深层次卷积神经网络模型中的模型性能退化的问题,得到了更好的性能。

图1 ResNet典型残差单元结构示意图Fig.1 Architecture of ResNet model

常用的ResNet结构网络深度分别为18、34、50、101和152,主要针对多维数据,而信道编码的数据是二元序列,为一维数据。因此,本文结合问题的难度,选择基于Pytorch 中的ResNet-18、ResNet-50网络结构进行调整,构造适用于信道编码的ResNet网络模型,其中,基于ResNet-50模型用于对编码结构的识别,ResNet-18用于对码序列起点的识别。将原网络中,卷积核“1×1”“3×3”“7×7”变成“1×1”“1×5”“1×7”,卷积方式由二维卷积变为一维卷积,得到网络结构示意图如图2所示。

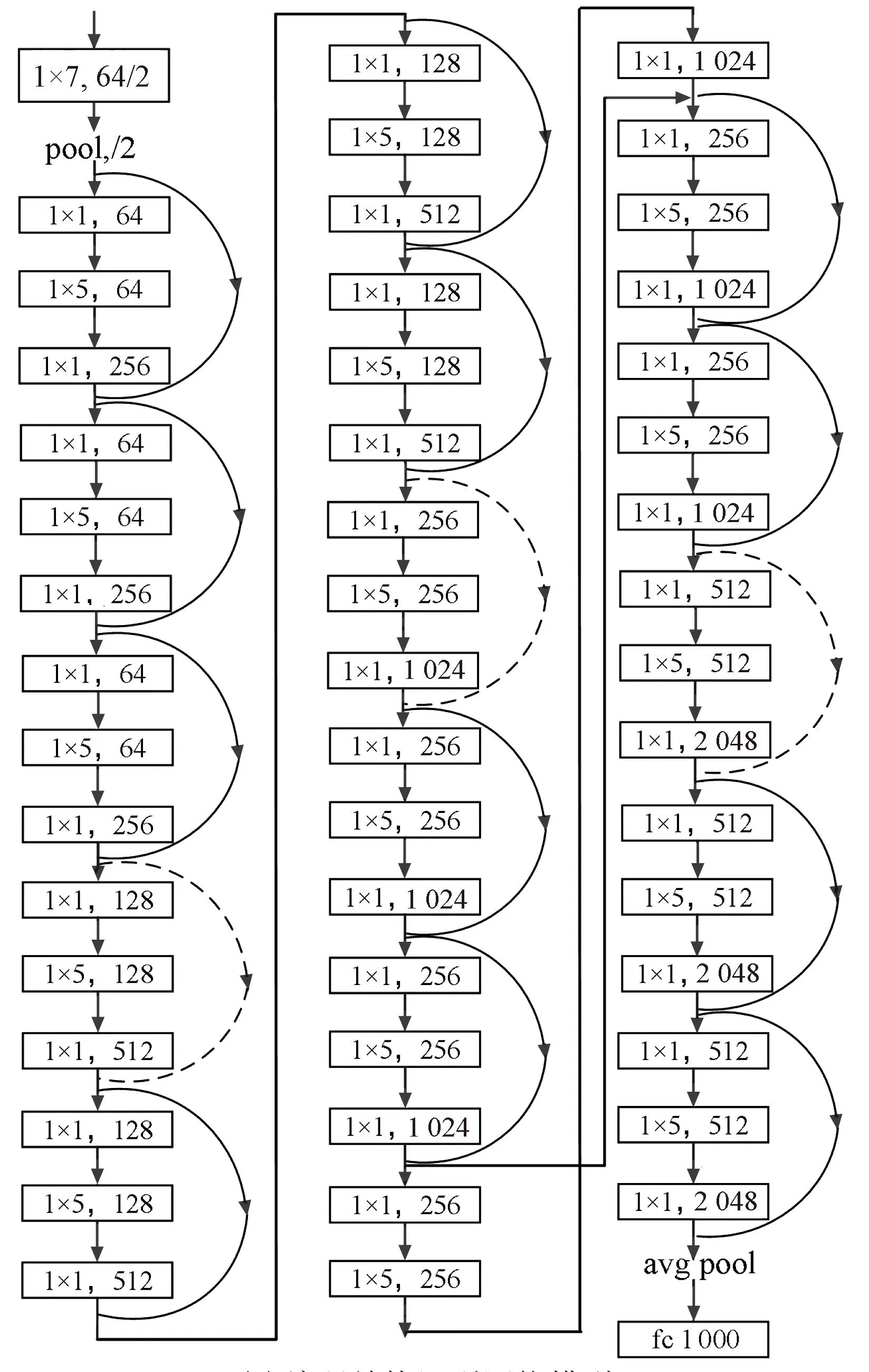
(a) 编码结构识别网络模型

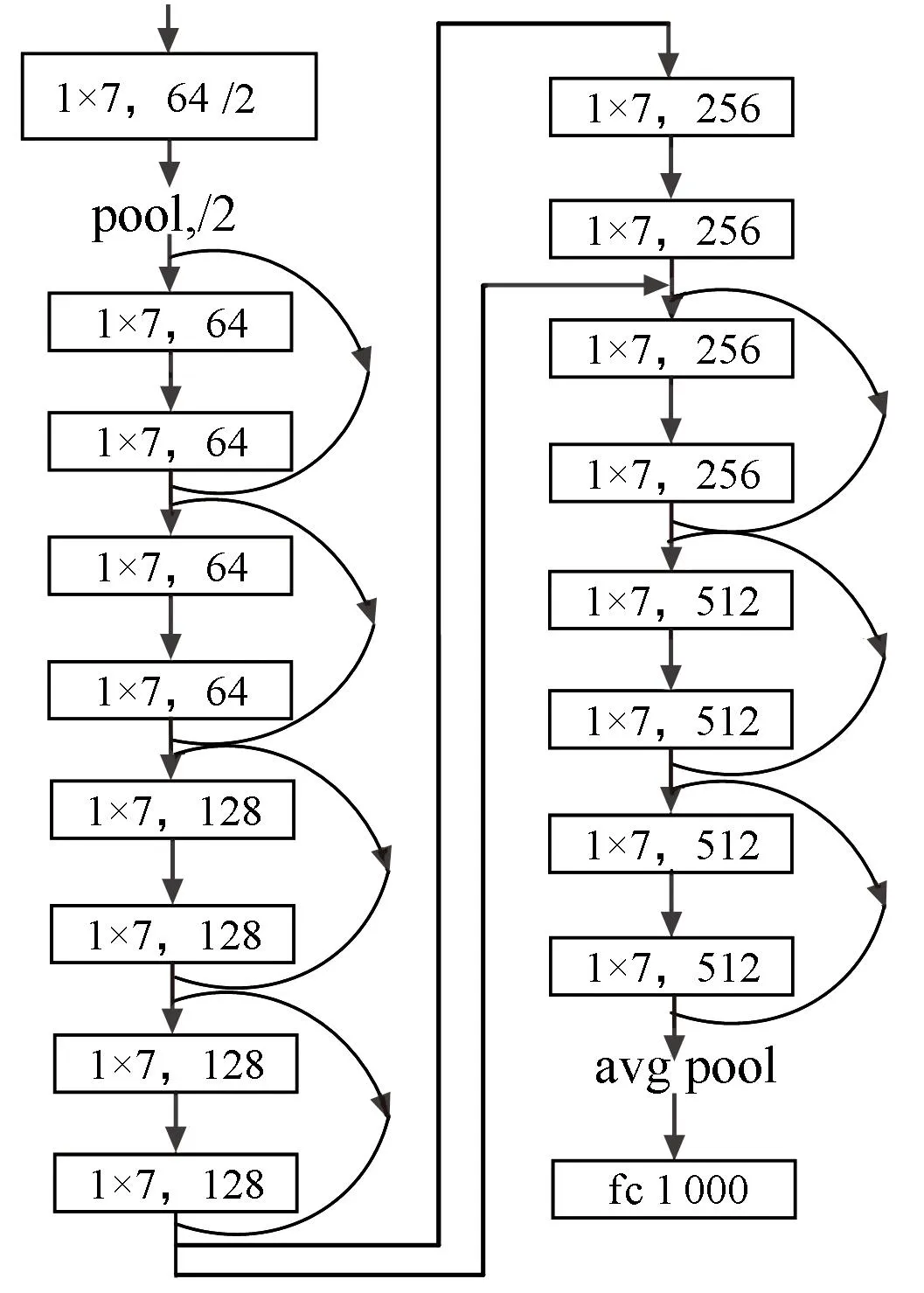
(b) 码序列起点识别网络模型图2 本文调整后的ResNet模型Fig.2 Adjusted ResNet model

2.2 网络数据样本生成

本文采用监督学习算法,基于常用的(n,1,m)卷积码在不同信噪比下构造数据样本,并对网络进行训练,实际识别时将待识别数据序列输入网络即可得到识别结果。根据文献[15],本文选取码长分别为2、3、4,编码存储级数为1～7的共21种常用码,用来构造数据。由前文分析可知,经解调等预处理后,最终影响识别效果的是误比特率和码字起点,因此可以利用计算机仿真软件非常方便地构造数据集。对于每一组码长n和存储级数m下,选取误比特率为0(即无误码)、0.01～0.09共10种情况,比特序列起点离码字起点为0～n-1共n种情况,分别在每种组合下构造30 000个200 bit长度的数据,其中错误比特根据编码序列长度和误比特率随机加入。同时,考虑卷积编码序列中前后比特的相关性,为了保证每个数据之间彼此独立,并不从一条编码数据中顺次截取数据。而是每次随机生成长度为1 000 bit的数据序列,然后按误比特率随机加入误比特,最后根据设置的数据起点从中截取长度为200 bit的数据。

2.3 模型训练与识别步骤

训练编码结构识别模型时,将所有数据送入网络进行训练,总样本数为1.89×107;训练编码序列起点识别模型时,分别选取对应码长、编码存储级数下n种样本序列起点、10种误比特率下n×10×30 000个样本进行训练,共需训练21个识别模型。两种网络训练均按4∶1的比例随机划分数据,得到训练集和验证集。

根据以上分析,总结基于ResNet的(n,1,m)卷积码识别步骤如下:

① 针对表中所示的21种(n,1,m)卷积码,按1～21 依次进行编号,对于每种编号下卷积码,利用Matlab软件按照2.2节所示生成训练样本;

② 将所有样本混合均匀后按4∶1的比例随机划分数据,得到编码结构识别训练集和验证集;分别选取对应码长、编码存储级数下n种样本序列起点、10种误比特率下n×10×30 000个样本,得到21个子样本集,各自混合均匀后按4∶1的比例随机划分数据,得到编码序列起点识别训练集和验证集;

③ 基于Pytorch框架分别构建图2所示的编码结构识别网络模型和编码序列起点识别网络模型,将训练集样本输入各自网络进行训练,并根据验证集情况不断调整网络参数,直到在验证集上结果最优;

④ 对于待识别的卷积码序列,按长度200 bit划分得到多个数据样本,输入到编码结构识别网络模型,根据统计结果确认待识别的编码结构,然后将编码序列从起点开始,每次间隔码长n划分序列得到多个数据样本,输入所对应编码结构的编码序列起点识别模型,根据统计结果确认待识别的编码起点,识别完成。

3 仿真验证与分析

仿真软件基于Windows 10 64位系统,数据产生基于Matlab R2020a 64位,程序设计基于Pycharm 2021.01社区版,Pytorch框架版本为1.5.1,cuDNN版本为7.6.1。硬件配置为:Intel(R) Core(TM) i9-10900X CPU @3.7 GHz,128 GB RAM,Nvidia GeForce RTX 2080Ti。

3.1 方法有效性验证

按2.2节生成训练集和验证集,输入网络进行训练,迭代30次后统计测试集上每种编码类型的识别成功率,得到的混淆矩阵如图3所示。

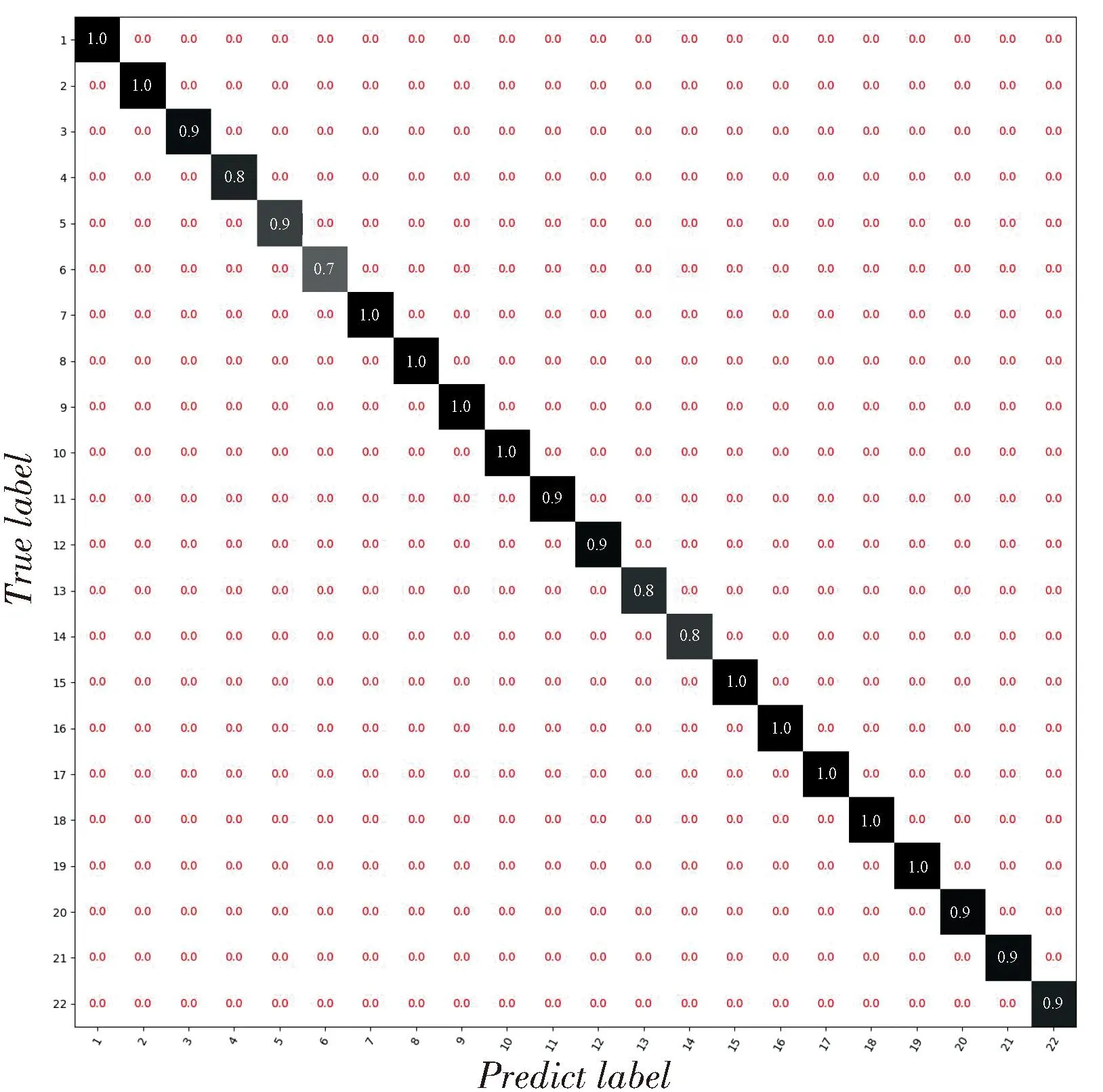
图3 21种编码样式综合识别准确率Fig.3 Comprehensive recognition accuracy of 21 convolutional coding structure

图中,纵轴代表样本的实际标签,横轴代表网络预测的标签,二者对应的红色数值表示实际标签对应样本被识别为预测标签对应编码样式的概率,即矩阵对角线处的数值表示21种编码样式在不同误比特率下的综合识别准确率。可以看出,对于21种编码样式,在误比特率为0.01～0.09时,综合识别准确率至少大于77.3%。进一步地,按2.2节相同的方法生成数据序列,从中随机截取长度为200 bit的数据,每种情况下生成3 000个样本。列出所有编码样式随误比特率的识别准确率变化曲线,结果如图4所示。可以看出,在误比特率小于0.03时,对所有编码样式的识别准确率均达到90%以上,甚至部分编码样式在误比特率为0.09时识别准确率达到了97%。这证实了本文所提方法的有效性。

(a) 1/2码率卷积码识别结果

(b) 1/3码率卷积码识别结果

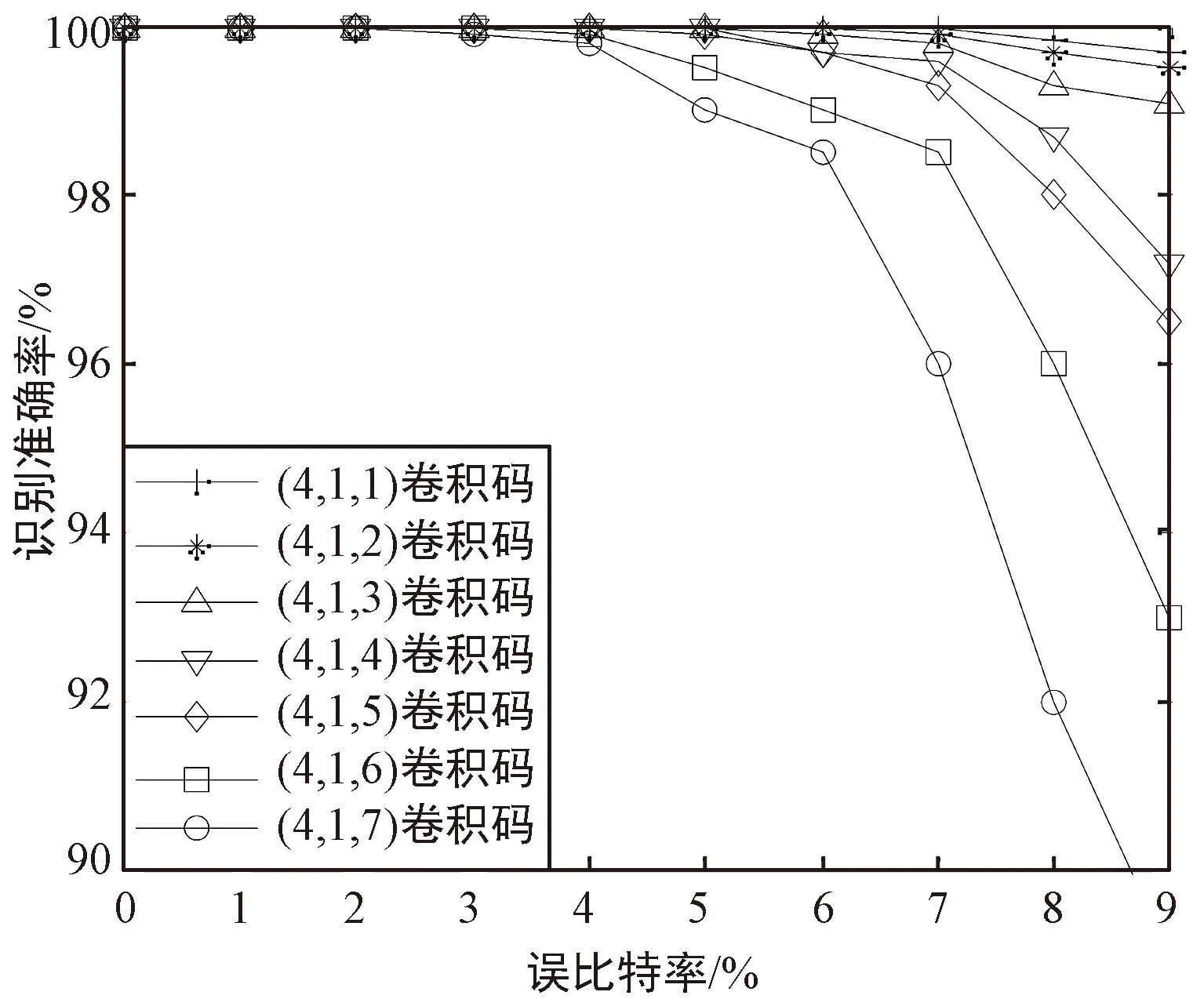
(c) 1/4码率卷积码识别结果图4 不同误比特率下卷积码识别准确率Fig.4 Recognition accuracy of convolutional codes under different bit error rates

对于编码序列起点识别,以(2,1,5)、(3,1,5)、(4,1,5)卷积码为例,在训练集上完成网络训练后,在验证集上的统计每种编码起点的识别成功率,得到的混淆矩阵如图5所示。

(a) (2,1,5)卷积码识别结果

(b) (3,1,5)码率卷积码识别结果

(c) (4,1,5)码率卷积码识别结果图5 编码起点识别结果Fig.5 Recognition result of coding starting point

可以看出,在不同情况下,每种起点情况的识别准确率都在96%以上。证实了本文所提方法的有效性。

3.2 与传统方法的对比

对卷积码识别,目前常用的方法主要是基于矩阵分析的方法和基于检验关系遍历验证的方法。下面主要从误比特率的适应性、计算复杂度、对数据长度的需求,以及码序列起点、码长和编码记忆长度对识别的影响等几方面进行对比,说明本文方法的优势之处。

3.2.1 识别性能对比

首先将本文方法对误比特率的适应性与文献[9]中基于矩阵分析的方法、文献[16]中基于最大似然检测的方法进行识别性能对比。选取(3,1,5)卷积码进行研究,由于不同方法所需的数据量并不相同,为了对比的客观性,此处主要考虑各种方法的最佳识别性能(即各种方法均满足识别所需的条件),得到结果如图6所示。

图6 不同方法识别性能对比Fig.6 Comparison of recognition performance between different methods

可以看出:

① 在理想情况下,本文的识别准确率与文献[16]中方法基本相当,明显优于文献[9]中方法,能在误码率为0.09时达到90%以上的识别概率;

② 两种对比方法在码长增大时识别模型更容易受到误比特的影响,导致识别率下降,本文方法在码长增大时识别率反而上升,可能是因为码长较大时编码数据包含的特征更明显,从而使网络更容易被训练。

同时,还应考虑到不同方法在识别时需要的编码参数先验知识并不相同。本文方法和文献[9]中方法不受先验知识的影响,直接将接收序列输入识别模型即可识别出对应的码长、编码记忆长度、生成多项式等参数,而文献[16]中方法需要预知码长、校验多项式阶数以及编码起点等知识,否则无法建立有效的方程进行识别。在实际应用场景下先验知识往往很难获取,因此文献[16]中方法的运用限制更大。

3.2.2 计算复杂度对比

对于本文方法,计算量主要在于网络的训练过程,但由于网络模型可以提前训练,而实际识别时往往需要近实时处理,因此,与文献[9,16]中的方法进行计算量对比时,主要对比识别时的计算量,对于本文方法即测试过程的计算量。

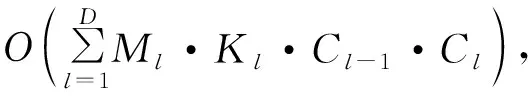
Ml=(Ml-1-Kl+2Pl)/Sl+1。

(10)

根据图4可知,网络包含卷积层数为49,卷积核长度取值为1或5,P取值为1或3,S取值为1或2,根据以上参数可以计算识别所需的计算复杂度。文献[9]中方法计算复杂度为Ο(25·L3/14),其中L取值为49;文献[16]中方法计算复杂度为Ο(N·n·(K+1)·2n(K+1)),其中n为码长,N为建立的方程组系数矩阵的行数,K为校验多项式的最高阶数。计算文中21种卷积码的计算复杂度如图7所示。

图7 不同方法计算复杂度对比Fig.7 Comparison of calculation complexity between different methods

可以看出,本文方法的计算复杂度保持恒定,在编码参数较小时大于两种传统方法,但随着编码参数的增大,基于最大似然检测的方法计算复杂度逐渐超过本文方法。

3.2.3 对数据长度的需求

本文识别方法网络训练的数据可以用通过计算机仿真生成,识别时所需的数据量与网络训练时选择的样本长度相同,恒定为200,而文献[9,16]中的方法往往与编码参数有关。文献[9]建立分析矩阵的列数要大于编码约束长度n·(m+1),在本文选择的21种编码方式下,取列数为30,行数为35,每行的起点间隔取12,则建立分析矩阵的过程所需数据量至少为438。文献[16]方法与误比特率、方程解的重量(即解向量中1的个数)有关,误比特率越高、方程解的重量越大,所需数据量越多。本文取校验多项式阶数为K=「(m+1)/2⎤,方程解的重量为ω=「n(「(m+1)/2⎤+1)/2⎤,误比特率取0.09,则所需数据量为:

(11)

计算21种编码方式所需的数据长度,结果如图8所示。可以看出,本文识别方法所需数据长度小于两种对比方法,特别是文献[16]中的方法,在码长、编码记忆长度较大情况下差距能达到数百倍。

图8 不同方法识别对数据长度的需求对比Fig.8 Comparison of sequence length needed for recognition between different methods

4 结束语

本文提出了一种基于ResNet的(n,1,m)卷积码盲识别新方法,将图像识别领域常用的神经网络模型经改造应用于信道编码识别领域,由网络提取不同编码参数下的差异特征,改变了传统人工提取特征进行卷积码参数识别的思路,可有效提升高误比特率下的识别准确率,且识别所需数据量有效降低,更适用于非合作条件下的信道编码盲识别。

下一步将重点关注删余卷积码、线性分组码、Turbo码等编码类型和参数的识别,将基于深度学习的识别模型扩展至其他编码类型,进一步提升实际工程应用价值。