初中数学应用题教学中数学建模法的应用

曾文玲(广东省珠海市第十三中学 519000)

培养学生的数学思维是数学教学的基本要求,也是确保学生能够有效地将课本知识迁移应用到社会生活实践中,解决实际问题的关键。应用题是数学知识与实际情境的有机结合,该类题型要求学生必须具备良好的语言文字理解能力、数学关系分析和知识的整合应用能力等。然而,在现实中不少学生这方面的能力比较欠缺和薄弱,导致其对应用题总是束手无策。本文结合笔者经验,分析和探讨数学建模法在初中数学应用题教学中的应用价值和方法。

一、数学建模法概述

数学建模法是一种将现实问题抽象成数学模型,并利用数学方法求解的方法。该方法将实际问题中的各种要素和变量通过关系模型和方程式进行描述,以便于学习者对问题实质的深度分析和解决。数学建模法在科学研究、工程技术、经济管理、教育教学等领域都有广泛应用,可以帮助使用者更好地理解和解决实际问题。但它要求建模者必须具备一定的数学知识、良好的问题分析能力与思维创新能力,以及探究合作和沟通能力等。

二、数学建模应用于初中数学应用题教学的价值

通过数学建模的训练不仅能够提高学生解决实际问题的能力,还能助力其数学思维的发展和创新意识的培养。在初中数学应用题教学中,数学建模具有重要价值。

1.帮助学生准确理解题意

数学建模对于学生准确理解题意起到了重要的作用。在解决实际问题时,学生往往需要从文字描述中提取出关键信息并将其转化为数学语言。通过数学建模,学生能够学会使用数学符号来表示问题中的各个要素,进而厘清思路,准确把握问题的要义。

2.帮助学生建构关系模型

数学建模可以帮助学生建构问题的关系模型,即将实际问题转化为数学问题,并建立数学模型。通过将问题拆解为不同的因素和变量,并明确它们之间的相互影响关系,学生可以更好地理解问题的结构和特点。同时,学生还能培养运用数学知识和技巧解决实际问题的能力,提高数学思维的灵活性和创造性。

3.帮助学生实现一题多解

数学建模可以帮助学生实现一题多解,即通过不同的模型和方法来解决同一个问题。实际问题往往存在多种解法,而传统的算式运算教学往往只强调单一的解法。通过数学建模,学生可以发掘问题的多个角度和解决途径,培养他们的思维灵活性和创新能力。同时,学生还能体验到数学的美和魅力,提高对数学的兴趣和学习动力。

三、数学建模法解决应用题的步骤及具体应用

1.数学建模法解决应用题的一般步骤

数学建模法主要是将实际问题转化为数学问题,并通过数学建模的方法进行求解和验证,从而得出与实际情况相符合的数学结论。使用数学建模法来解决应用题,一般包括四大步骤,分别是:问题转化、模型构建、模型处理和模型检验。

(1)问题转化

首先,根据题意,仔细阅读问题,理解问题所涉及的背景和条件。然后,将实际问题转化为数学问题,提取出问题中的关键信息和要素。这可以包括设计变量、约束条件、目标函数、已知数据等。

(2)模型构建

在模型构建阶段,需要对问题进行抽象和概括,根据问题的特点选择适当的数学对象、函数或模型。这包括确定数学关系、建立方程组或函数表达式、确定几何关系等。同时,还需要根据实际情况进行必要的假设,并考虑各个因素之间的相互作用。

(3)模型处理

在模型处理阶段,我们利用已有的数学知识和方法,对建立的数学模型进行求解和分析。这可以包括代数运算、方程求解、函数图像分析、优化方法等。通过运用适当的数学原理和技巧,可以得出数学结论,即解决问题的数学表达式或函数。

(4)模型检验

在模型检验阶段,需要将得到的数学结论还原到实际问题中进行验证。这可以通过对模型的结果进行实际应用和比较,或者进行实际数据的收集和实验验证。如果得到的数学结论和实际问题是一致的,那么模型就是有效的。

2.数学建模法解决应用题的具体应用

(1)在函数类应用题中的应用

函数是初中数学的重点内容,其知识应用范围极其广泛。初中数学关于函数类的应用题如运动问题、成本利润问题、产量与效益问题、比例问题等。数学建模法的关键是将这些实际情况进行形象的数学化处理,通过将问题转化为适当的函数表达式,并利用函数的性质和关系进行求解与分析。在初中数学应用题教学中,教师通过借助数学建模法能够帮助学生准确识别和理解应用题中的变量关系,进而建立数学模型,提高他们分析与解决实际问题的能力。下面结合实例分析数学建模法的应用:

【例题1】

某饮料厂为了开发新的产品,用A、B两种果汁原料各19kg、17.2kg,试制甲、乙两种新型饮料共50kg,下表是试验的相关数据:

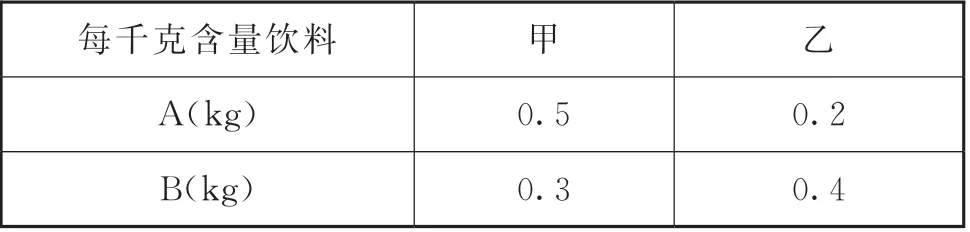
每千克含量饮料 甲 乙A(kg)0.5 0.2 B(kg) 0.3 0.4

【问题】

(1)如需要配置甲种饮料x千克,请根据题意列出不等式组,并求出其解集。

(2)若已知甲种饮料的成本为4元/kg,乙种饮料的成本为3元/kg,设两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果推算,配置多少千克的甲种饮料才能保证两种饮料的成本总额最少。

【解法】

解答本题的关键,一是明确已知条件,二是分析数量关系,三是结合函数思想进行求解。

首先,让学生仔细审题,结合题干阐述和表格信息,已知A、B两种饮料的原料总量、配置的甲乙两种新型饮料总量,以及配置比例。可以列出不等式组:

进而求得28≤x≤30,即甲种饮料的配置量介于28～30kg范围内。

其次,根据“成本总额=甲种饮料成本+乙种饮料成本”这个数量关系式,结合问题(1)的计算结果,可以列出函数表达式:

y=4x+3(50-x)=x+150(28≤x≤30)

最后,运用函数的性质从而确定最低总成本。由一次函数性质可知y值与x值正相关,即x值增大则y值也相应增大,因此当x=28 时,甲、乙两种饮料的成本总额最少,即y=28+150=178(元)。

(2)在方程类应用题中的应用

初中数学中涉及的投资决策问题、生态环境保护问题、生产计划问题、交通运输类,以及求解最大(小)值等问题,都可以利用数学建模法来帮助学生将抽象、复杂的问题进行形象化、简单化处理,将其中的数学关系转化为对应的方程或方程组,然后通过解方程的方式来求解未知量,并利用方程的性质和关系进行问题的分析和推理。

【例题2】

某县政府为美化城市环境,改善居民的生活质量,计划投入4700万元兴建一个综合型城市公园。为保证公园早日建成,承建方经预算后决定先期拿出项目投资总额的0.4%用于购买某种绿化树进行环境绿化。在首次从某林场购买了价值8万元的绿化树后,通过与林场协商获得优惠条件,即一次性购买绿化树超过10万元时,可以获得每棵树20元的价格优惠。于是在第二次购买时,承建方将剩余的预算资金一次性投入,比第一次多购回200棵绿化树。

【问题】承建方通过两次购买,共购回多少棵绿化树?

分析:对于方程类应用题的解答,应该结合题意合理设置未知数,然后列出等量关系,最后进行求解并检验所得数据是否符合实际情况。以本题为例,解法如下:

【解法】

若设承建方第一次购买了x棵绿化树,那么其第二次的购买数为(x+200)棵,结合题意可以列出其方程式:

通过计算得到:x1=400,x2=-2000。通过验证发现x2的数值明显不符合实际。因此,承建方第一次购买的绿化树为400棵,进而求得第二次购买了600棵,两次共计购得1000棵绿化树。

(3)在几何类应用题中的应用

在实际生产和生活中,有很多现实问题需要借助空间几何知识进行计算解答。部分初中生的生活经验和认知水平有限,不能在头脑中形成具体情境,难以有效理解题意。通过利用数学建模思想,基于对应用题中的几何变量关系进行分析,可以帮助学生建立形象的数量关系模型,从而准确理解题意,顺利解决相关问题。

【例题3】

某居民小区为改善公共居住环境,决定通过自主筹资1600元,在小区原有的一处梯形空地上种植各种花木。该空地的上、下部分的长度分别为10m 和20m,垂直高度12m,由于中间有围栏分隔,使其被划分为①、②、③、④四个不同面积的地块区域。

【问题】

(1)该小区居民计划在①区域种植向日葵,种植成本为8 元/平方米;已知种满该区域花费了160元,问种满与其相似的②区域需要花多少费用?

(2)该小区的剩余区域可以栽种玫瑰花和茉莉花两种花木,其中玫瑰花的单价为12元/平方米,茉莉花的单价为10 元/平方米,问应选择哪种花木,才能刚好用完所筹集的资金?

【解法】

本题是关于绿化美化工程的一道实践题,涉及空间几何知识和绿化工程知识,解决该类问题的第一步是根据题中信息,建立一个梯形模型,其中AC和BD两条围栏相交于M点,并将整个梯形地块分为了四个区域(①～④),如图1所示。通过建立该几何模型实现了题中问题信息的直观呈现,便于学生更好地理解题意。

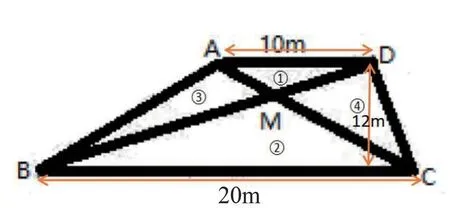
图1 某小区内一块梯形空地

第二步,指导学生认真观察几何模型,同时回顾相似三角形的相关知识,这里需要用到“相似三角形的面积比等于其相似比的平方”“相似三角形对应高之比等于其相似比”。然后得到以下解答:

(1)根据题中所述①、②区域相似,即△AMD∽△CMB,因此S△AMD∶S△CMB=1∶4

根据种满△AMD 所在地块花了160元,则可以知道:

S△AMD==20m2,因此S△CMB=20×4=80m2,由此可以计算得出,种满②区域需要花费640元。

(2)由梯形面积公式可以求得,SABCD=(10+20)×12÷2=180m2,S△AMB+S△DMC=180-(S△AMD+S△CMB)=80m2

综上,剩余区域假如选择种植玫瑰花,则160+640+80×12=1760元;假如选择种植茉莉花,则160+640+80×10=1600元。因此,选种茉莉花能够刚好用完所有资金。

四、结语

应用题是初中数学的一个重难点内容,不仅考查学生的社会生活认知能力,而且对学生的数学逻辑思维、知识综合应用能力等提出了较高要求。借助于数学建模法,结合题中信息建立数学模型,将相关问题与关系转化为数学表达式,便于学生深入理解题意,并启发他们的解题思路,同时也起到培养和提升学生数学思维和模型建构能力的作用,为今后的学习打下坚实基础。