有向图的外独立双罗马控制

张新鸿 ,代潇娜 ,李瑞娟

(1.太原科技大学 应用科学学院,山西太原 030024;2.山西大学 数学科学学院,山西太原 030006)

§1 引言

本文所采用的术语和符号参见文献[1]. 如无特别说明, 本文所涉及的图都是非空的, 有限简单有向图. 设D=(V(D),A(D))是一个有向图, 其中V=V(D)为D的顶点集,A=A(D)为D的弧集.D的顶点数称为D的阶数. 如果对于任意两个顶点u,v ∈V(D), 有uv ∈A(D)或者vu ∈A(D)或者uv ∈A(D)和vu ∈A(D), 则称该有向图为半完全有向图. 特别地, 如果对于任意两个顶点u,v ∈V(D), 有uv ∈A(D)或者vu ∈A(D), 则称该有向图为定向图. 如果uv是D的一条弧, 则称u是v的一个内邻(或v是u的一个外邻). 对于顶点v ∈V(D),N-(v) =(v) ={u ∈V -v:uv ∈A(D)}和N+(v) =(v) ={w ∈V -v:vw ∈A(D)}分别称为v的开内邻集和开外邻集. 类似地,N-[v] =N-(v)∪{v}和N+[v] =N+(v)∪{v}分别称为v的闭内邻集和闭外邻集.d-(v) =(v) =|N-(v)|和d+(v) =(v) =|N+(v)|分别称为v的内度和外度.δ-=δ-(D) = min(v) :v ∈V(D)}和δ+=δ+(D) = min(v) :v ∈V(D)}分别称为D的最小内度和最小外度. 类似地, ∆-= ∆-(D) = max(v) :v ∈V(D)}和∆+= ∆+(D) =max(v):v ∈V(D)}分别称为D的最大内度和最大外度.

对于D的一个顶点子集,若其中任意两个顶点互不相邻,则称该顶点子集为D的一个独立集.独立集的最大基数称为独立数,记为α(D).设S是D的一个顶点子集,如果N+[S]=V(D),则称S是D的一个控制集.控制集的最小基数称为控制数,记为γ(D).具有最小基数的控制集称为γ(D)-集.设Q是D的一个顶点子集,若N+[Q]=V(D)且N+[Q]Q是D的一个独立集,则称Q为D的一个顶点覆盖.顶点覆盖的最小基数称为顶点覆盖数,记为β(D).具有最小基数的顶点覆盖称为β(D)-集.

1999年,Stewart[2]提出了关于罗马控制的问题,之后Cockayne[3]等学者进一步定义了罗马控制函数并进行了深入的研究[4-6].随着研究的不断深入,产生了多种罗马控制的衍生类型,如双罗马控制[7-8],三罗马控制[9],全罗马控制[10],符号罗马控制[11]等.

假设h:V(D)→{0,1,2,3}是定义在D上的一个函数,如果函数h满足

(1) 每个赋值为0的顶点至少有两个赋值为2的内邻或一个赋值为3的内邻;

(2) 每个赋值为1的顶点至少有一个赋值为2或3的内邻;

(3) 所有赋值为0的顶点都是不相邻的,

则称函数h是D的一个外独立双罗马控制函数,记为h=(V0,V1,V2,V3),其中Vi={v ∈V(D) :f(v)=i},i ∈{0,1,2,3}.一个外独立双罗马控制函数h的权重ω(h)=一个外独立双罗马控制函数的最小权重称为外独立双罗马控制数,记为γoidR(D).如果ω(h)=γoidR(D),则称函数h是D的一个γoidR(D)-函数.

文献[12-13]研究了无向图的外独立双罗马控制.本文将外独立双罗马控制的概念推广到了有向图中,研究了有向图的外独立双罗马控制数的界,并在此基础上给出了外树的外独立双罗马控制数的下界.同时,进一步刻画了外独立双罗马控制数的Nordhaus-Gaddum型不等式.

§2 预备知识

观察2.1设D是一个有向图,h=(V0,V1,V2,V3)是D的一个γoidR(D)-函数,则

(1)V2∪V3是D的一个控制集.

(2)V(D)V0是D的一个顶点覆盖.

引理2.2设D是一个有向图,则必存在一个γoidR(D)-函数h=(V0,V1,V2,V3)满足|V0|0.

证利用反证法.假设h=(V0,V1,V2,V3)是D的任意一个γoidR(D)-函数且|V0|=0,那么显然有|V3|=0.进一步地,可以断言|V1|0.否则,|V2|=|V(D)|,这样就有ω(h)=2|V2|=2|V(D)|.任取D中一个内度不为零的顶点v,定义函数g:V(D)→{0,1,2,3}使得g(v)=1,g(x)=2,其中x ∈V(D){v}.容易验证g是D的一个外独立双罗马控制函数,且ω(g)=2|V(D){v}|+1=2|V(D)|-1<2|V(D)|=ω(h),与h是D的一个γoidR(D)-函数矛盾,故|V1|0.任取顶点w ∈V1,由外独立双罗马控制函数的定义,w必存在一个赋值为2的内邻,记为z.定义函数f:V(D)→{0,1,2,3}使得f(w)=0,f(z)=3,f(y)=h(y),其中y ∈V(D){w,z}.不难验证,f是D的一个γoidR(D)-函数且|V0|0,矛盾.

引理2.3设D为n阶半完全有向图,那么γoidR(D)≥n+1.

证设h=(V0,V1,V2,V3)是D的一个γoidR(D)-函数.因为D的任意两个顶点都相邻,所以由外独立双罗马控制函数的定义中条件(3)可知|V0|≤1,此时|V1|+|V2|+|V3|≥n-1.下面分两种情形进行讨论.

情形1|V0|=0

此时就有|V2|≥1,那么|V1|+|V2|+|V3|=n,可得

情形2|V0|=1

此时必有|V3|≥1或|V2|≥2.如果|V3|≥1,那么

如果|V2|≥2,那么

当∆+(D)=n-1时,引理2.3的界是紧的(参看图1(b)).

图1 (a):一个7阶有向星图S,设f是S的一个γoidR(S)-函数,令f(v0)=3,f(vi)=0,i ∈{1,··· ,6},则γoidR(S)=3.(b):一个6阶完全有向图D,设g是D的一个γoidR(D)-函数,令g(v0)=3,g(v1)=0,g(vi)=1,i ∈{2,··· ,5},则γoidR(D)=7

§3 外独立双罗马控制数的界

命题3.1设D是一个n阶有向图,则γoidR(D)≥δ-(D)+2.

证设h=(V0,V1,V2,V3)是D的一个γoidR(D)-函数.如果|V0|=0,那么|V3|=0,进一步有γoidR(D)≥n+1≥δ-(D)+2.如果|V0|0,那么任取顶点x ∈V0.由外独立双罗马控制函数的定义可知,有N-(x)⊆V1∪V2∪V3.又x在V3中至少有一个内邻点或在V2中至少有两个内邻点,故|V2|≥2或|V3|≥1,这样就有

在有向星图和完全有向图上,命题3.1的界是紧的(参看图1).

命题3.2设D是一个n阶有向图,则γoidR(D)≤n+γ(D).

证设S是D的一个γ(D)-集,易知h=(V0,V1,V2,V3)=(∅,VS,S,∅)是D的一个外独立双罗马控制函数,那么γoidR(D)≤ω(h)=2|S|+|VS|=n+|S|=n+γ(D).

引理3.3设D是一个n阶有向图,则β(D)+2≤γoidR(D)≤3β(D).

证设Q是D的一个β(D)-集.由β(D)-集的定义知h=是D的一个外独立双罗马控制函数,因此γoidR(D)≤3|Q|=3β(D).

定理3.4设D是一个n ≥2阶的有向图且δ-(D)≥1,则γoidR(D)=β(D)+2 当且仅当下列条件之一成立.

(1) 存在一个顶点z ∈V(D)满足d+(z)=n-1.

(2) 存在两个顶点z1,z2使得V(D)=N+[z1]∪N+[z2],并且D[N+(z1)∩N+(z2)]的每一个最大独立集也是D的一个最大独立集.

证“必要性” 由引理2.2,设是D的一个γoidR(D)-函数且满足0.又由γoidR(D)=β(D)+2以及引理3.3中的(2)式,可得这样,就有1且下面分两种情形进行讨论.

情形1

设={z}.由外独立双罗马控制函数的定义可知,D中所有赋值为0和赋值为1的顶点均被z控制,因此d+(z)=n-1.

β(D)≤|V(D)I1|<|V(D)I|=|V(D)()|+2=+2=γoidR(D)-2,与β(D)=γoidR(D)-2矛盾.因此,I是D的一个最大独立集.

“充分性” 下面分两种情形进行证明.

情形1存在一个顶点z ∈V(D)满足d+(z)=n-1

若D中的任意两个顶点都相邻,则β(D)=n-1.由引理2.3可知,γoidR(D)=n+1=β(D)+2.否则,D中至少存在两个顶点互不相邻.设I1是D的一个最大独立集,由d+(z)=n-1可知,z/∈I1.因此,令易知h1是D的一个外独立双罗马控制函数.这样就有γoidR(D)≤ω(h1)=n-α(D)-1+3=n-α(D)+2=β(D)+2,又由引理3.3可知γoidR(D)=β(D)+2.

情形2存在两个顶点z1,z2使得V(D)=N+[z1]∪N+[z2],并且D[N+(z1)∩N+(z2)]的每一个最大独立集也是D的一个最大独立集

设I2是D[N+(z1)∩N+(z2)]的一个最大独立集,则I2也是D的一个最大独立集.注意到z1,z2/∈I2,令h2=易知h2是D的一个外独立双罗马控制函数.由δ-(D)≥1,有β(D)=|V(D)I2|.因此γoidR(D)≤ω(h2)=|V(D)I2| -2+4=|V(D)I2|+2=β(D)+2,又由引理3.3,就有γoidR(D)=β(D)+2.

§4 外树

本节刻画外树的外独立双罗马控制数的下界.

设T是一棵有向树,如果存在一个顶点r ∈V(T),使得d-(r)=0,且对任意的顶点v ∈V(T){r}都有d-(v)=1,则称T是一棵以r为根的外树,记为.若d+(v)=0,则称v为的一个叶子,与v相邻的顶点称为的一个茎.如果一个茎至少相邻两个叶子,则称为的一个强茎.对于顶点,若d+(w)/=0,则称w为的一个分支点.设w是的一个分支点,若从顶点w到顶点v有一条弧wv,则称v为w的一个子节点(或称w为v的一个父节点).注意到,在任意的一棵外树中,从根r到任意一个顶点有且仅有一条路,故记λ(v)是从根r到顶点v的路长,则depth()=max{λ(v)称为外树的深度.特别地,当depth()=1时,称为一个有向星图.图2是一棵以r为根的外树,v1,v2是两个叶子,w是一个与v1,v2相邻的强茎,x是w的父节点(或w是x的子节点),x是v1的一个祖先(或v1是x的一个子孙),depth()=4.

图2 外树

定理4.1设是一棵n ≥2阶的外树,则γoidR()≥2β()+1.

证当depth()=1时,是一个有向星图,因此β()=1,这样就有

当depth(-)≥2时,显然有n ≥3.下面对的阶n使用数学归纳法进行证明.

n=3时,易知γoidR()=5=2β()+1.设对于阶为k ≤n -1的任意树,都有γoidR()≥2β()+1.接下来分两种情形进行讨论.

情形1至少包含一个强茎u

设v是与强茎u相邻的一个叶子,外树=T{v}.由和的结构以及顶点覆盖的定义可知,β()=β().进一步地,由外独立双罗马控制数的定义以及归纳假设可得

情形2中不存在强茎

设v是的一个叶子且λ(v)=depth(),w是v的父节点,x是w的父节点.

子情形2.1d+(x)≥2

因为λ(v)=depth(-),所以x的所有子节点只可能是叶子或茎.令=,此时β()=β()+1.设f是的一个γoidR()-函数.定义上的一个函数f1使其满足f1(z)=f(z),其中z ∈V(T′).因为N+T(w)=v且f是的一个γoidR()-函数,所以f1是的一个外独立双罗马控制函数.

子情形2.1.1f(x)=3

由f是的一个γoidR()-函数易知,f(w)=0,f(v)=2.又f1是的一个外独立双罗马控制函数,故γoidR()≤ω(f1)=γoidR()-2,这样就有γoidR()≥γoidR()+2≥2β()+3=2β()+1.

子情形2.1.2f(x)=2

在此情形下,不难知道f(w)+f(v)=3.因为的所有茎都不是强茎,所以x最多有一个叶子x′.

若x的所有子节点中有唯一的一个叶子x′,则f(x′)=1.令g是上的一个函数且满足(g(x′),g(x),g(w),g(v))=(0,3,0,2),g(y)=f(y),其中y ∈V(){x′,x,w,v}.易知g是的一个外独立双罗马控制函数,且ω(g)=γoidR()-1<ω(f),矛盾.

若x的所有子节点都是茎.设w1是x的一个不同于w的子节点,是w1的子节点.由λ(v)=depth()可知是一个叶子,则f(w1)+f()=3.令g1是上的函数且满足g1(x),g1(w),g1(v))=(2,0,3,0,2),g1(y)=f(y),其中y容易知道g1是的一个外独立双罗马控制函数,且ω(g1)=γoidR()-1<ω(f),矛盾.

子情形2.1.3f(x)=1

类似地,有f(w)+f(v)=3.因为f(x)=1,所以depth()≥3.否则,x为的根,这就意味着x将无法得到其它顶点的支援,从而与外独立双罗马控制函数的定义矛盾.

若x的所有子节点中有唯一的一个叶子x′,那么f(x′)=2.定义上的一个函数h满足(h(x′),h(x),h(w),h(v))=(0,3,0,2),h(y)=f(y),其中y ∈V(){x′,x,w,v},可以验证函数h是的一个外独立双罗马控制函数,且ω(h)=γoidR()-1<ω(f),矛盾.因此,x的所有子节点都是茎.进一步地,考虑下面两种情形.

(a)d+(x)=2

设w1是x的一个不同于w的子节点,是w1的一个子节点,这样就有f(w1)+f()=3.由f1是的一个外独立双罗马控制函数且γoidR()≤ω(f1)=γoidR()-3可知

(b)d+(x)≥3

在此情形下必存在x的两个不同于w的子节点w1和w2,设分别是w1,w2的子节点,同理有类似地,定义上的一个函数h1满足其中y可知h1是的一个外独立双罗马控制函数,且ω(h1)=γoidR(T)-1<ω(f),矛盾.

子情形2.1.4f(x)=0

与子情形2.1.3类似,此时f(w)+f(v)=3且depth()≥3.

断言x的子节点情况只能为以下三种情形之一.(a)x的子节点中除w外还包含一个叶子;(b)x的所有子节点都是茎且d+(x)=2;(c)x的所有子节点都是茎且d+(x)=3.

证如若不然,则或者x的子节点中既有叶子,又至少有一个不同于w的茎;或者x的所有子节点都是茎且d+(x)≥4.

若x的子节点中既有叶子,又至少有一个不同于w的茎,那么设w1是不同于w的一个茎,是w1的子节点.这样就有f(x′)=2,f(w1)+f()=3.定义上的一个函数l满足

则l1是的一个外独立双罗马控制函数,且ω(l1)=γoidR(T)-1<ω(f),矛盾.下面证明当情形(a-c)成立时,定理的结论成立.

若(a)成立,则由f(x)=0可知,f(x′)=2.因为f1是的一个外独立双罗马控制函数,所以γoidR()≤ω(f′)=γoidR()-3.又γoidR()≥2β(T′)+1且β(T)=β(T′)+1,故γoidR()>2β()+1.

若(b)成立,则设w1是x的一个不同于w的子节点,w′1是w1的子节点,这样就有f(w1) +f()=3.又f1是的一个外独立双罗马控制函数且γoidR()≤ω(f1)=γoidR()-3,故γoidR()>2β()+1.

若(c)成立,则必存在x的两个不同于w的子节点,记为w1和w2.设,分别是w1和w2的子节点,则f(w1)+f()=3,f(w2)+f()=3.由f1是的一个外独立双罗马控制函数且γoidR()≤ω(f1)=γoidR()-3可知,γoidR()>2β()+1.

子情形2.2d+(x)=1

设=,此时β()=β()+1.设f是的一个γoidR()-函数,定义上的一个函数f2使其满足f2(z)=f(z),其中z ∈V(T′).与子情形2.1类似,f2是的一个外独立双罗马控制函数.

如果f(x)=3,那么f(w)+f(v)=2.又f2是的一个外独立双罗马控制函数,故γoidR()≤ω(f2)=γoidR()-2,这样γoidR()≥2β()+1.

如果f(x)=2,那么f(w)+f(v)=3.又f2是的一个外独立双罗马控制函数,故γoidR()≤ω(f2)=γoidR()-3,这样γoidR()>2β()+1.

如果f(x)=0或f(x)=1,那么f(w) +f(v)=3.由子情形2.1.3和2.1.4的证明可知,depth()≥3.又f2是的一个外独立双罗马控制函数,故γoidR()≤ω(f2)=γoidR()-3,因此γoidR()>2β()+1.

综上所述,若是一棵n ≥2阶的外树,则γoidR()≥2β()+1.

不难验证,当depth()=1,即是一个有向星图时,定理4.1的界是紧的.

§5 Nordhaus-Gaddum型不等式

定理5.1设D是一个n ≥2阶的有向图,则γoidR(D)+γoidR(D)≥n+3.

由图3可知,定理5.1的界是紧的.

图3 (a)一个n阶有向图D:设h是D的一个γoidR(D)-函数,令h(v0)=3, h(vi)=0,i ∈{1,···,n -1},则γoidR(D)=3;(b)D的补图: 设h1是的一个γoidR()-函数,令h1(v1)=3,h1(v0)=h1(v2)=0, h1(vi)=1,i ∈{3,···,n-1},则γoidR()=n

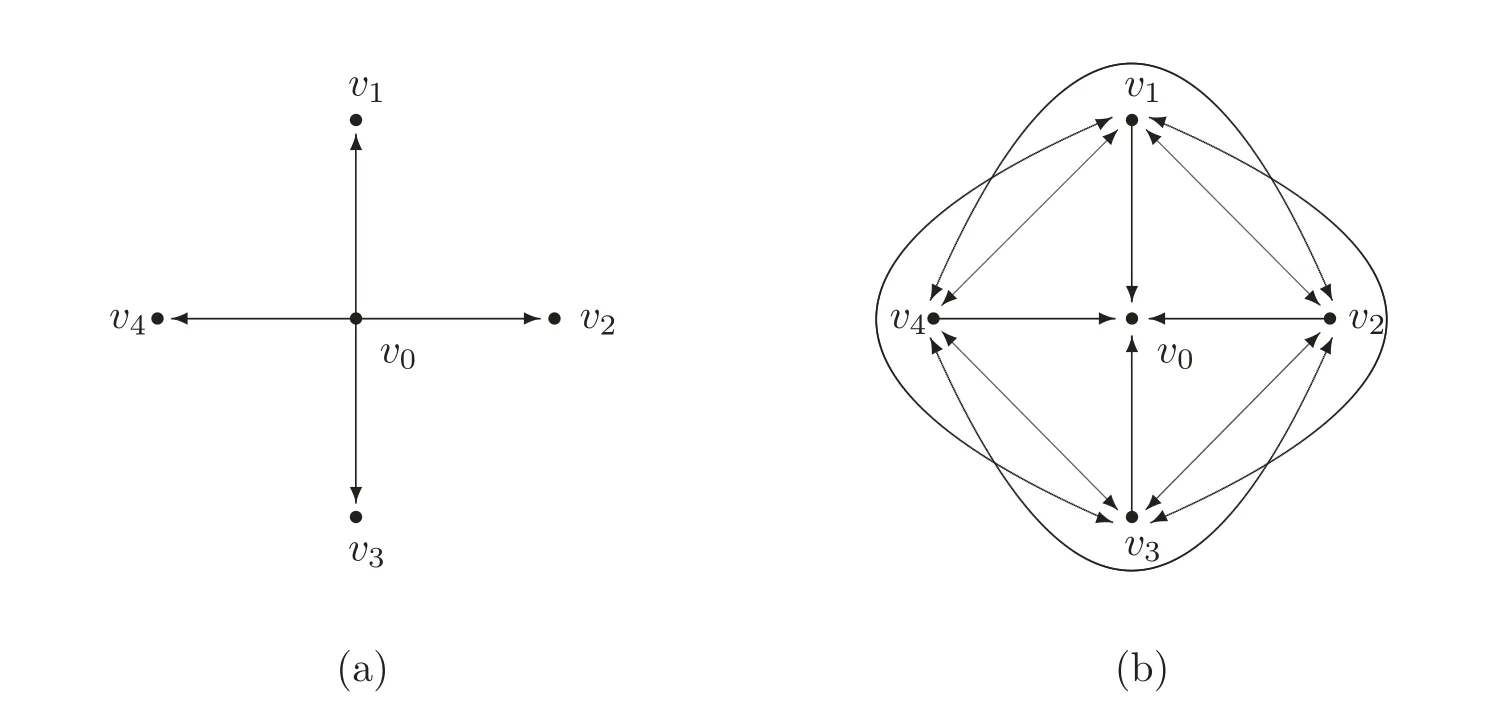
图4 (a)一个5阶有向星图S: 设g是S的一个γoidR(S)-函数,令g(v0)=3,g(vi)=0,i ∈{1,2,3,4},则γoidR(S)=3;(b) S的补图: 设g1是的一个γoidR()-函数,令g1(v0)=0, g1(v1)=3, g1(vi)=1, i ∈{2,3,4},则γoidR()=6

定理5.2设D是一个n ≥2阶的定向图,则γoidR(D)+γoidR()≥n+4.