基于空间自回归的地价指数模型
2023-12-14戴韫卓吴潇然叶荣兵赵子楠胡日成张荣茂
戴韫卓 ,吴潇然 ,叶荣兵 ,赵子楠 ,胡日成 ,张荣茂
(1.浙江省自然资源网上交易中心,浙江杭州 310007;2.浙江大学数学科学学院,浙江杭州 310058)
§1 引言
土地价格在国民经济体系中扮演着重要作用,它不仅是土地要素参与宏观调控的经济杠杆[1],同时也是评估宏观经济的重要指标[2].如何有效地分析地价的变动规律,对于我国土地市场健康有序的发展将具有十分重要的意义.
地价指数是衡量土地价格随时间变化的趋势与幅度的指标,反映一个城市各类土地价格变化及其总体综合平均变化趋势.有效构建地价指数的统计模型与实时动态预测,是推进自然资源要素配置,优化市场环境,降低交易成本,加强内部监管,强化社会监督,促进廉政建设的有效保证.
然而,由于地价自身的特性:(a) 数据不可重复性(同一块地往往只一个交易价格);(b) 非平稳特性(价格与地理位置紧密相关),导致数据之间的结构往往具有较大的差异,而具有相近结构的数据量往往很少,使得价格指数的统计建模特别困难,见[3-4].目前,国内对地价指数统计建模的理论研究较少.业界大多使用加权平均的简单方法进行计算,见[5-9],这样的指数往往无法有效地反映地价的非平稳特性和动态变化,难以被用于预测.
地价往往随着时间的变化,所处的区域不同,外界环境因素影响呈现空间和时间上的动态变化.在时域上,同一时间拍卖的土地受相同的市场大环境,政策影响,其成交价格相关性也更强.在空间上,相邻地块共同的周边环境与配套决定了他们的价格也有所相关.至于外界因素,影响地价的外部因素不胜枚举,很大一部分因素与地块空间位置相关,如路网稠密程度,公共交通站点个数,自然景观数量,与商务生活中心的距离等.此外,地价还受到用地类型,容积率等与空间位置无关的外生变量的影响.
为了捕捉地价在时空上的动态信息,同时考虑外生变量对其影响,本文提出一类带外生变量空间自回归的地价建模方法,该方法通过提取同一时期内地价指数的共同趋势来刻画地价指数,并基于自回归时间序列实现了地价指数的趋势预测.笔者也将所提的空间自回归模型和自回归时间序列应用于浙江省土地招拍挂数据,并通过该数据来说明具体实施过程及预测效果.从实验的结果可以看出,所提出的模型符合过往的经验及市场判断,具有较好的拟合度.
§2介绍地价指数的空间自回归建模;§3节介绍空间自回归模型在浙江省地价指数上的应用;§4总结本文所做的工作及今后的展望.
§2 模型
2.1 空间自回归模型及其参数估计
同一时期的土地招拍挂成交数据,其亩均成交单价很大程度上依赖于地块所处地理位置,在空间中产生聚集效应.例如,相比于郊区土地,市中心附近的出让地块将具有更高的价格水平.为了捕捉土地成交价格在空间上的相依性,本文使用空间自回归模型(Spatial Autoregressive Model,即SAR)见[10],对同一时期内土地交易数据进行建模.SAR模型被广泛应用于空间数据的统计建模,其表达形式为
其中y为所研究区域的因变量,W为权重矩阵,X为外生变量构成的设计矩阵,∊为噪声项,ρ和β为模型的待估参数.对于拟合SAR模型,一个关键的步骤便是参数估计,本文采用极大似然估计方法,首先令A=I-ρW,可以将模型简化为
其中∊是独立标准正态噪声项.该模型可以看作关于参数的非线性模型f(y,X,θ)=∊,其中θ=(ρ,β′)′是未知参数向量,f是广义非线性泛函.尽管噪声项∊有着良好的联合分布,但其不可观测的性质导致必须通过y构造似然函数,进而需要引入将∊转化为y的Jacob行列式
接下来便可基于噪声项的联合正态性加之Jacob行列式得到观测值y的对数似然函数
从上式可以看出,最大化似然函数L相当于最小化Jacob修正后的偏差平方和,Jacob行列式|A|中的空间项使其不同于普通最小二乘估计,所以需要保证|A|>0,即|I-ρW|>0.进一步,进行极大似然估计需要对待估参数求解一阶偏导数并令其等于0得到参数估计值
使用数值方法求解上述非线性方程组,即可得到参数ρ与β的极大似然估计.
2.2 地价指数建模
为保证同一时期内数据量充足,本文按季度划分土地交易数据.对于土地成交价格数据,其空间聚集效应体现在权重矩阵W上.此外,地块价格受用地类型影响较大,如住宅用地单价往往高于工业用地与商服用地,也受土地规划的容积率影响,容积率决定地价成本与土地开发商最终回报的比例.因此建模中将容积率上限与用地类型作为外生变量加入设计矩阵X,得到按季度划分的空间自回归模型
其中yt为pt×1维向量,代表第t期内的pt个出让地块的亩均成交单价.Ut=(µt,µt,···,µt)为模型的共同截距项,FAR为政府规划的该地块容积率上限,D为以用地类型分类标准的哑变量.
权重矩阵W的选取使用KNN (k-最近邻) 原则,确定每个数据点固围非零权重的个数.选取
其中#Yt表示第t个季度样本的数量.接着,计算每个点i和周围最近k个点的距离dij,j ∈KNN(i),取权重为
然后使用上一节所述方法估计待估参数.
由于权重矩阵W的估计需要用到地块的地理位置信息,对于少量无坐标数据和坐标错误的数据,使用普通最小二乘法建立线性回归模型
对于上述空间自回归模型,空间自回归项与外生变量为每个样本的异质部分,而Ut=(µt,µt,···,µt)为同一季度内所有样本的共同趋势项,因此获得每个季度内的模型及其参数值后,选取共同截距项µt衡量地价指数,反映市场行情的变化情况.以第一季度数据(t=1)为基准期,并对地价指数进行位置与尺度放缩,此操作不改变序列的趋势,但使其落入通常市场认可的指数区间.由此可以得到第t季度的地价指数indext为
由上述步骤得到的指数序列indext是一个季度时间序列,其ACF图呈现短记记忆性.因此本文考虑使用自回归模型(Autoregressive Model,即AR)进行预测,AR模型的定阶可使用AIC,BIC等信息准则,当样本量较小时,信息准则定阶效果较差.本文基于土地市场的经验数据,用之前四个季度的数据预测本期,对指数建立AR(4)模型并进行点预测和区间预测.
§3 浙江省地价指数建模与分析
本文使用的数据为浙江省自然资源厅提供的时间跨度为2017年10月至2022年11月的浙江省各地市土拍数据,共计两万余条,每条数据包含一块出让土地的成交单价,成交时间,用地类型,容积率范围,土地所属行政区域与地块中心经纬度等指标.2018年10月以前数据大部分缺失经纬度信息,另有少量数据存在经纬度录入错误,对于该部分数据在提取截距趋势项时采用普通最小二乘法估计.
以宁波市数据为例,土地的亩均单价在空间上与随时间分布的图像如图1所示,可以看出土地价格在空间与时间上都呈现出非平稳的特性.
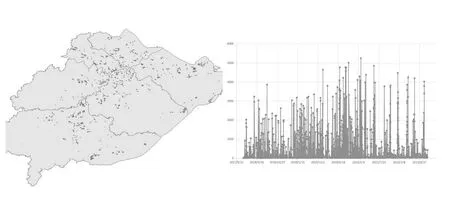
图1 宁波市土地拍卖价格的时空分布图
2.3 地价指数趋势拟合
根据§2的建模步骤,按季度划分土地成交数据,在每个季度内对带土地坐标的数据进行SAR模型建模,可以得到各季度内参数估计结果.以杭州市商品房数据为例,由于前四季度数据坐标信息缺失,仅使用普通最小二乘回归,从第五季度开始(即2018年第四季度起),各季度SAR模型参数估计结果见表1.
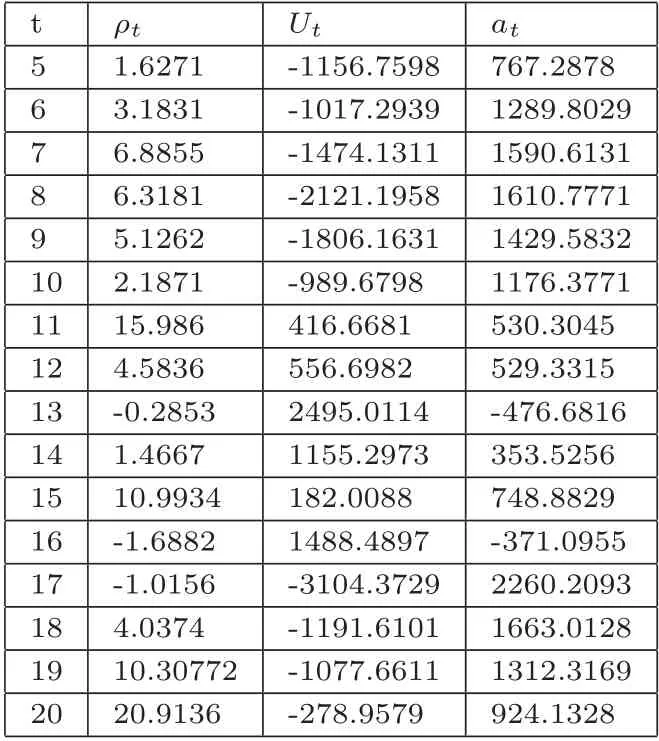
表1 杭州市商品房地价指数模型参数估计
得到SAR模型参数估计后,提取季度内共同趋势项Ut,进行量纲处理后得到地价指数的拟合曲线,本文分别处理了浙江全省数据,杭州市与宁波市两个副省级城市数据.全省数据共有67种用地类型,其中商品房,工业用地与商务金融用地三种类型的成交土地最多,关注度也最高.不同用地类型的地价指数趋势不尽相同,以宁波市数据为例,如图2所示,商品房的平均成交单价高于其他用地类型,由于市场也最为关注商品房土地的价格走势,接下来的数据分析中本文将重点关注此种用地类型.

图2 宁波市季度地价指数拟合
图2为浙江全省地价指数拟合曲线,该曲线各拐点与过往重要政策颁布,市场变化有较好的对应关系,见表2,证明本文方法得到的地价指数符合过往经验与市场预期.

表2 浙江省地价指数走势与实际市场情况对比
求得SAR模型的各项参数后,还可对各季度内土地平均价格进行样本内预测,得到的预测曲线与真实价格曲线如图4至图6所示.图4至图6显示,部分区域预测值与实际值高度重合,证明该模型有较好的拟合效果.
由于不同地块价格的数量级差距很大,本文使用均方相对误差作为模型误差的衡量标准,其定义为
其中yt为地价在第t季度的平均价格.图4至图6所述模型均方相对误差如表3所示.

表3 均方相对误差
对比地价指数趋势图(图2与图3)与平均价格趋势图(图4至图6),可以看出指数与地价的变化趋势并不完全一致,指数的变动通常比地价滞后一个季度左右,而地价指数比平均价格更能反应一定程度的宏观经济总体变化.以宁波数据为例,2020年第一季度至第二季度,平均价格仍在攀升(见图6),但地价指数已经下降(见图2).此时受疫情影响,市场低迷,地价指数较好捕捉到了这一市场变化.

图3 浙江省季度地价指数拟合
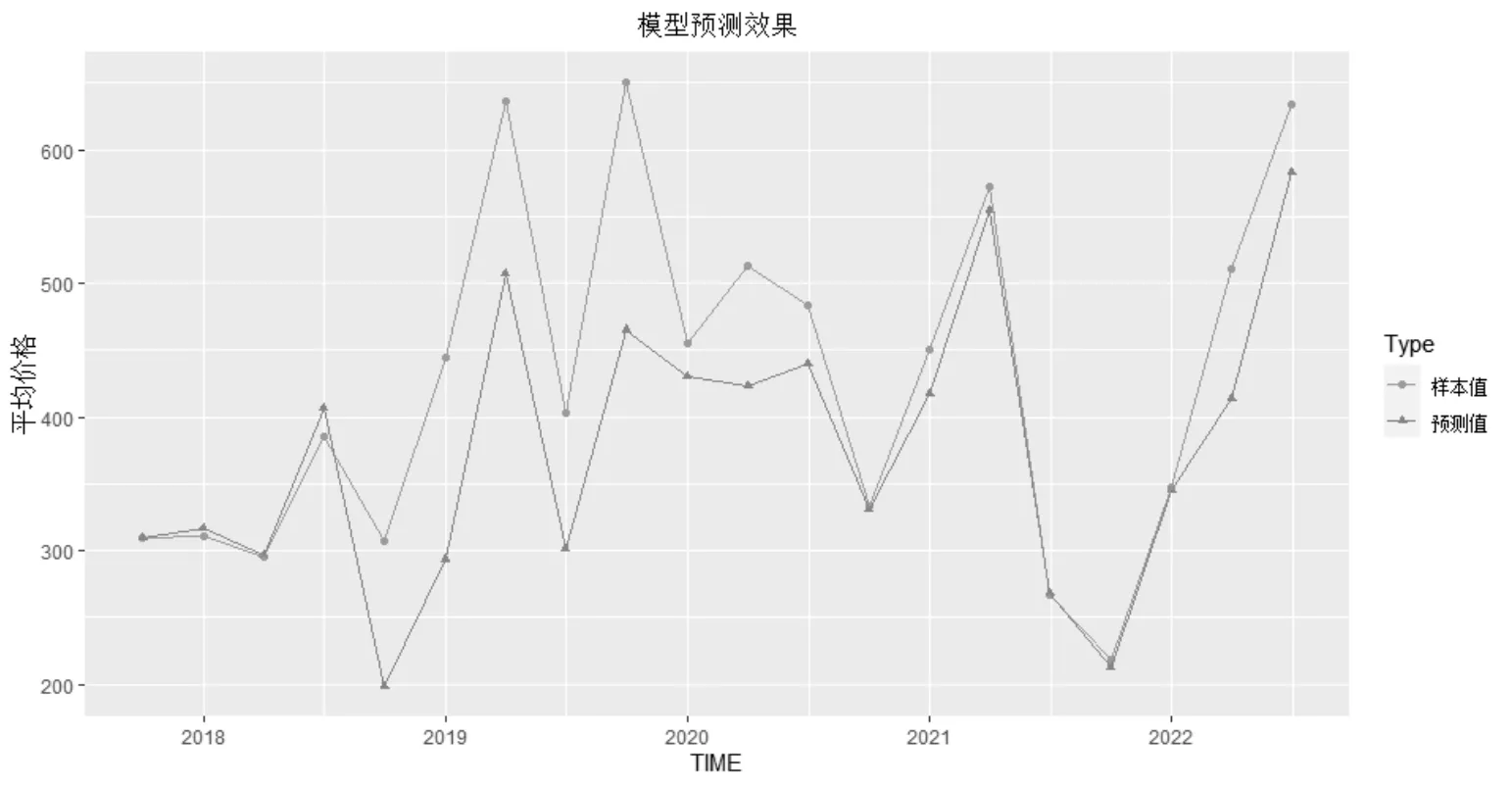
图4 浙江省季度平均地价预测
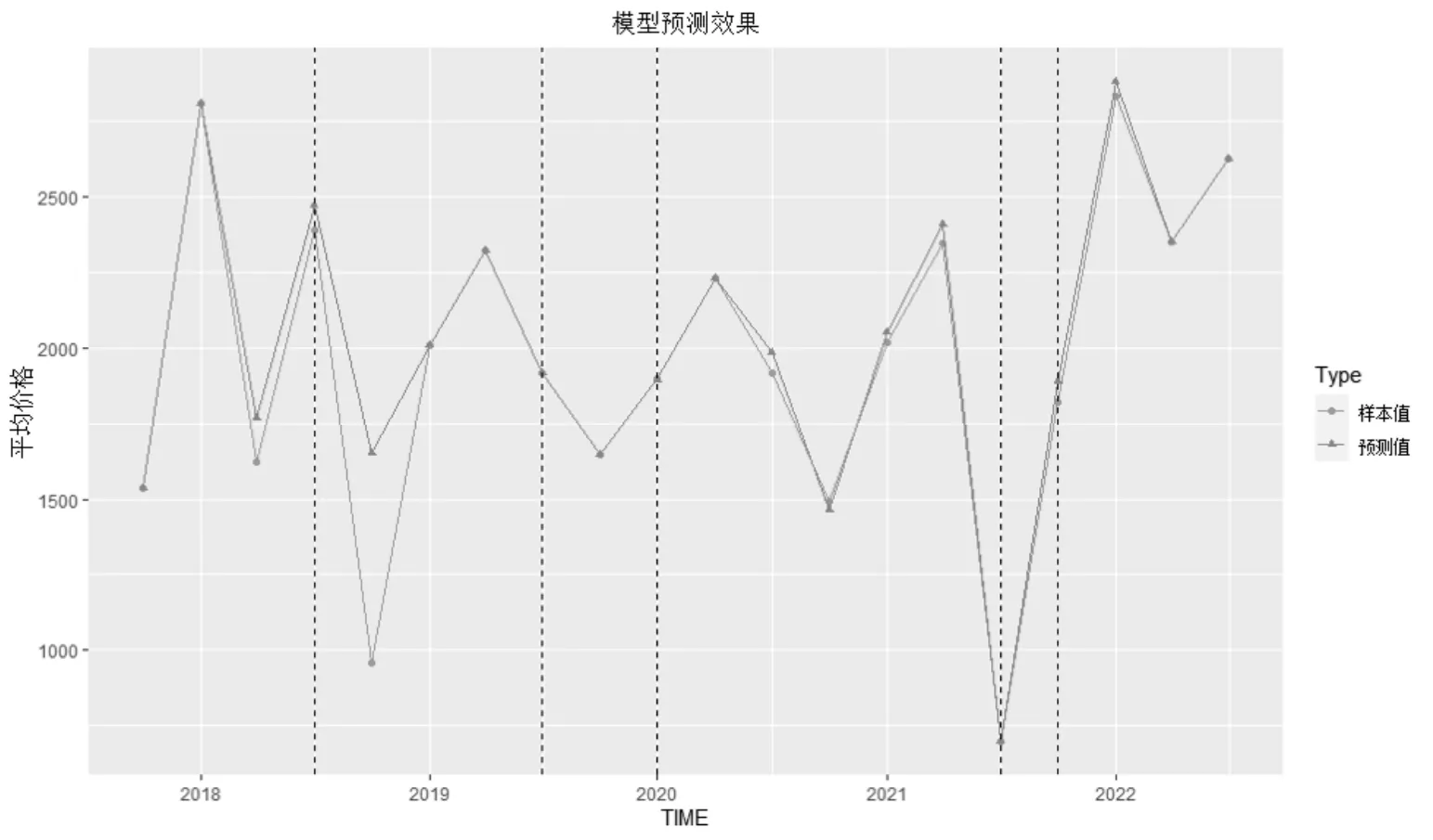
图5 杭州市季度平均地价预测
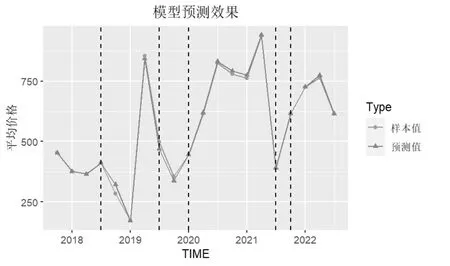
图6 宁波季度平均地价预测
3.2 指数动态预测
浙江省分用地类型的地价指数未来四季度预测如图7所示,三个类型用地的指数变化不尽相同,但大体趋势一致.预测结果表明2022年第四季度及2023第一季度地价指数有上升趋势,而在2023 年第二季度有下降趋势.预测的置信区间如表4所示.
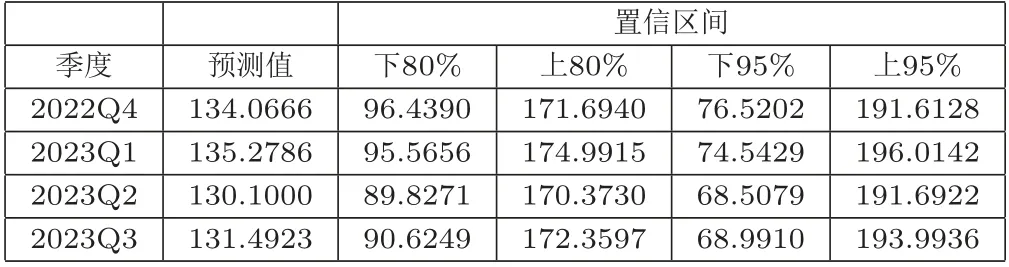
表4 浙江省地价指数未来四季度区间估计

图7 浙江省地价指数未来四季度点预测
2.4 地价样本外预测
本文提出的空间自回归模型还可用于地价的样本外预测.使用第t期的SAR模型预测第t+1期的地价,以宁波市t=18(即用2022年第一季度的模型对第二季度地价进行预测)为例,如图8所示,平均上看预测准确度较高,分每个地块看,预测值比真实值更加平滑,真实值的波动大,并且有统计意义上的离群点,异常点.图9为第18期地价预测值与真实值的箱线图,可以看出预测值的中位数大于真实值,但平均值小于真实值.
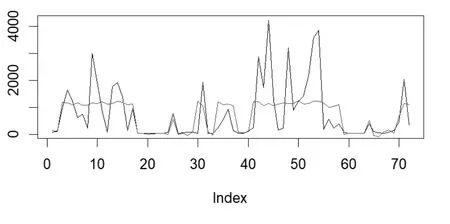
图8 宁波地价样本外预测(横坐标为第18期各出让土地地块,纵坐标为土地价格,红线为预测值)
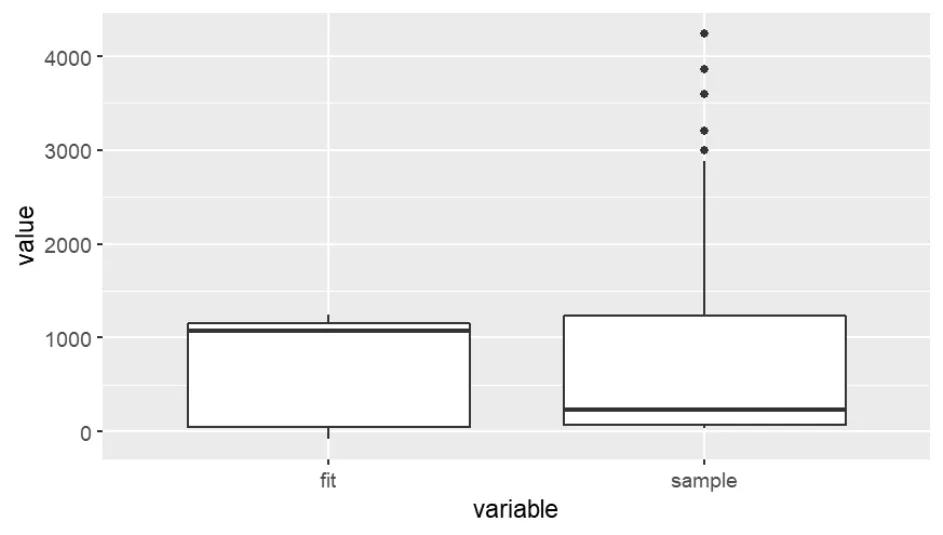
图9 宁波地价样本外预测箱线图
§3 结论
本文提出了一个基于空间自回归的地价指数拟合预测模型,能够较为准确并客观地刻画地价指数在过往的走势,符合市场经验认知.该模型首先利用空间自回归模型,刻画同一时期内不同拍卖地块在地理位置上的相依关系,再提取出共同趋势项,利用时间序列模型进行建模.本文所提出的方法均从数据本身出发进行数学建模,有别于传统方法只是对于历史价格的简单平均.实证分析结果表明本文提出的模型对浙江省地价指数有较好的建模效果.由于缺乏数据在时间上的重复观测,本文没有直接通过非平稳时空模型(见[11])来进行地价指数的建模,今后将尝试这方面的探讨.
