人口转型中生育观念传播模型的建立与分析
2023-12-14刘子建谭远顺庞建华
刘子建 ,刘 铭 ,谭远顺 ,杨 金 ,庞建华
(1.重庆交通大学 数学与统计学院,重庆 400074;2.广西科技大学 理学院,广西柳州 545006)
§1 引言
人口转型(Demographic Transition),是指一个国家或地区从工业化前的经济体制向工业化经济体制过渡时,伴随着的从高出生率高死亡率到高出生率低死亡率,再到低出生率低死亡率的现象[1-3].人口转型与生育率和老龄化,与人力资本和经济增长,与技术进步和农业人口转化,与收入分配和教育特别是女性教育等关系密切,众多学者已详细研究了人口转型的原因及所带来的经济和社会影响[4-10].文献[4]分析我国第七次人口普查数据,发现我国人口发展的主要矛盾正在从数量性压力向结构性压力转化,提出我国应明确人口新国情定位,顺应人口新国情要求,普及人口新国情教育,深化体制机制改革,创新社会治理新格局的重要建议.文献[5]分析了黑龙江省人口老龄化特征及老龄问题的成因,讨论了老龄化在劳动力供给,政府财政和创新创业方面对黑龙江省社会经济产生的负向效应,建议从优化劳动力供给结构,增强财政可持续性,鼓励“银色创业”三个方面进行应对.文献[6]综述了中国人口与经济问题的关系,指出人口结构而非人口总量才是影响经济增长的主要因素.文献[8]指出了农业人口的转型提高了农业劳动力的人力资本水平,带来了人口,物质,资本等农业技术进步所需的保障,推动了技术的进步,保证了农业的可持续增长.文献[9]利用具有内生储蓄和人力资本投资决策的代际重叠模型评估了中国人口变化对人力资本积累和总产出的影响.结果表明,与现状相比,教育份额和人均收入将随着生育率的反弹而下降,教育政策在减轻与高生育率相关的不良后果方面有效.文献[10]从理论和实证两方面研究了发展中国家的教育,性别差距和人口转型的关系,得到了技术进步解放了家务劳动从而导致了最初人口出生率增加,女性参加社会劳动的增加提升了教育的机会成本进而导致生育率下降,女孩教育投入的增加,性别教育差距的降低,提高了平均人力资本,加速了技术进步和经济增长的结论.
人口转型的直接结果是出生率和死亡率的变化.发达国家诸如美国,日本,德国等国家均在工业革命后进入了人口转型期.目前绝大多数发达国家已接近或完成人口转型,其死亡率和出生率均处于新的低水平上[3].我国因为较长一段时间的计划生育政策,出生率呈快速下降趋势.人口死亡率随着生活和医疗技术的提高,也呈下降趋势,但人口的自然增长率在近10 年下降较快,尤其2020 年仅有1.45 ‰(如图1 (a)).我国不同省份的人口自然增长率差距也较大,且并不乐观(如图1 (b)),这其中有人口流动的影响,但出生率的影响更为重要.联合国《世界人口发展展望(2019)》采用高,中,低三个方案(总和生育率—每个妇女育龄期生育孩子的总数—水平分别取2.3,1.8,1.3)对我国的总和生育率进行了预测(如图2),显示我国未来生育水平既有实现适度生育水平的可能性,更有停留在超低生育率水平的风险,表明未来生育政策优化及生育友好环境的重构将是关键.因此,研究群体生育观念及国家生育政策的改变对生育观念的影响具有现实意义.本文将具体研究人口转型过程中生育观念的传播对我国低生育率现象和人口增长的影响.
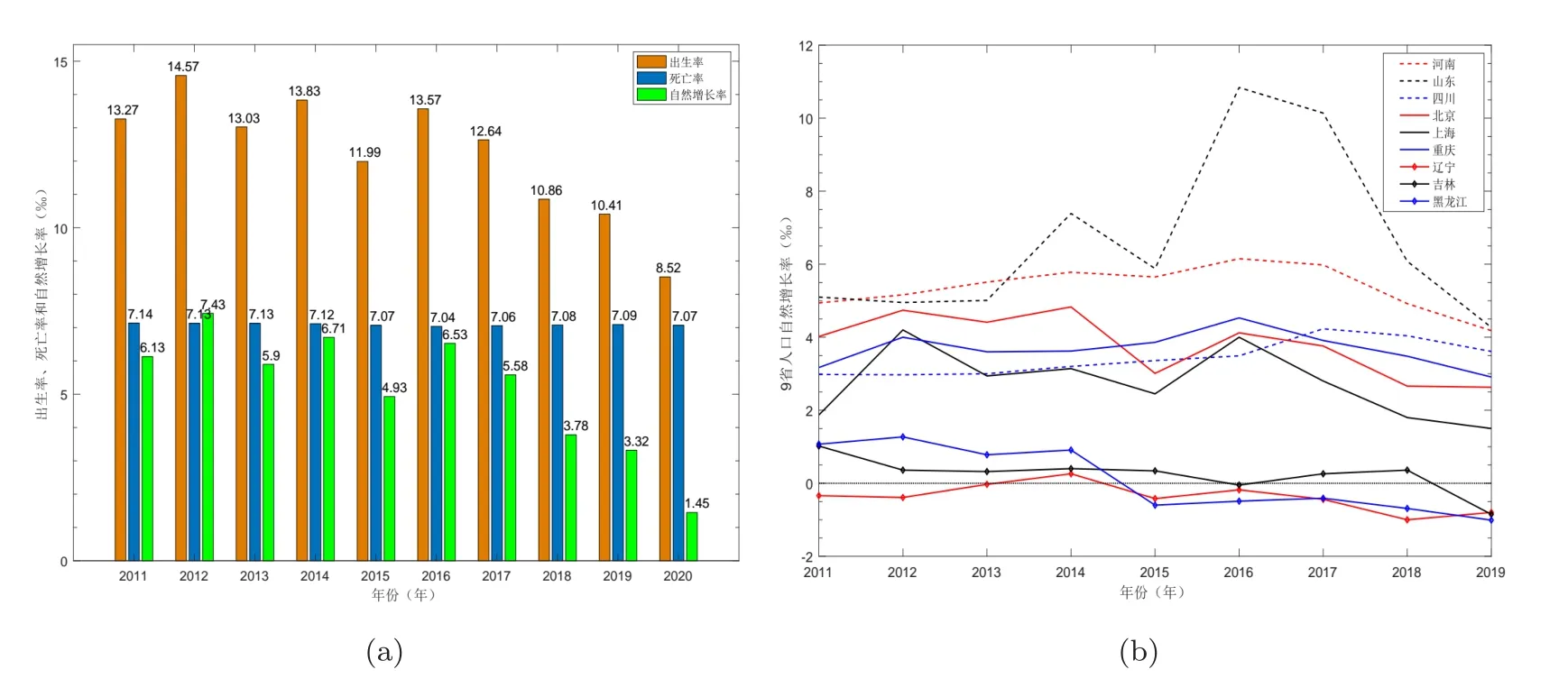
图1 (a) 2011-2020年我国人口的出生率,死亡率和自然增长率(数据来源:国家统计局) (b) 2011-2019年河北,山东,四川,北京,上海,重庆,辽宁,吉林,黑龙江9省市的人口自然增长率情况(数据来源:国家统计局)

图2 1960-2100年我国总和生育率变化及未来走向(数据来源:World Population Prospects 2019)
§2 模型建立
观念的传播和扩散问题,可以借助传染病模型进行建模研究.基于传染病模型并考虑个体接触传播这一假设,越来越多的学者利用传染病模型研究具有社会互动影响行为的诸如成瘾行为[11-13](吸烟,吸毒,饮酒等),观念认同度[14-17](幸福观,生育观,社会舆论,媒体影响)和饮食失衡或肥胖现象[18-19]等的传播特性,传播规律及社会影响.文献[14]建立了具有自发行为的SIRS谣言传播微分方程模型,指出了影响谣言传播的主要因素并提出谣言治疗策略.文献[20]建立SIS模型研究了具有从众偏见的文化特质传播问题,并将研究结果应用到酗酒行为.文献[21]结合传染病模型和Lotka-Volterra系统,建立模型
来刻画数量增加或衰减种群中生育观念的传播问题.其中S(t)表示t时刻高生育群体个体数量,即易感群体个体数量,I(t)表示t时刻低生育群体个体数量,即感染群体个体数量.b1和b2分别是易感群体和感染群体的Malthus增长参数,满足b1>b2.β>0为传染系数.作者研究指出,当生育观念侵入指数大于1 时,生育观念侵入成功,人口转型将会发生.本文考虑国家人口政策对我国人口出生率和总和生育率的影响[22-24],改进Inaba的模型,建立了考虑国家生育政策且具有饱和发生率的生育观念传播模型
(1)式中,a为国家对生育政策的干预力度.N=S+I.假设模型(1)中参数满足条件
(JS1)b1>0,b1>b2,β>0,k>0,a ≥0.
注1b2可正可负,b2>0表示低生育群体的出生率大于死亡率,b2<0表示低生育群体的出生率小于死亡率,a>0指国家采取鼓励生育的政策.
若无特别说明,本文总是假设条件(JS1)成立.记(1)式中第一个式子右端为g1(S,I),第二个式子右端为g2(S,I).论文首先研究了在无国家生育政策干预下生育观念传播模型的动力学行为.进一步讨论了国家实施鼓励生育政策后,生育观念的传播特性及我国人口的变化情况.最后通过数值例子讨论了国家生育政策干预力度对我国人口增长的影响.
§3 主要结论
本节将分析在无或有国家鼓励生育政策情况下(1)式的动力学行为,并说明这些动力学行为所蕴含的实际意义.
首先说明解的非负性.对任意非负初值(S(0),I(0)),由系统(1),对∀t>0有
假设(JS1)保证a ≥0,从而
即对任意非负初值,系统(1)的解非负.此结论亦完全符合实际生物学意义.
3.1 无国家生育政策干预(a=0)
此时模型(1)变为
(2)式中令g1(S,I)=g2(S,I)=0,有g1(S,I)+g2(S,I)=b1S+b2I=0.显然系统(2)必存在零平衡点E0=(0,0).进一步,因为b1>0,易知b2≥0时,系统(2)无正平衡点;而当b2<0时,有S=-b2I/b1,此时可建立系统存在正平衡点条件.
(1A) b2 >0
令v=I/N,显然0≤v ≤1.此时u=S/N=1-v.系统(2)两方程相加有
这里h(N)=b1-b2-β(1/N+k)-1.假设0 记h∞=limN→∞h(N)=b1-b2-β/k,则对所有N>0 都有h(N)≥h∞. 当h∞>0时 当h∞<0时,存在∊0>0 使得h∞+∊0<0.此∊0,(3)式说明存在T>0,当t>T时,N(t)满足h(N(t)) 综上,当t →∞时有 定义生育观念侵入指数 显然 依据低生育群体在总人口中人口数量占比,给出生育观念侵入成功的定义. 定义1若limt→∞v(t)=1,则称生育观念侵入成功且为完全侵入.若0 有如下结论. 定理1当低生育群体自然增长率b2>0时,若生育观念侵入指数R>1,则低生育群体的生育观念完全侵入到高生育群体;若R<1,则生育观念侵入不成功. 注2若b2>0,R=1,未能理论证明确切结论.数值实验可证明其会发生不完全的生育观念侵入,如图9 (b).注意到,例证虽具有局限性,但却能够说明会发生不完全生育观念侵入这一事实. 注3当b2=0时,若传染系数小于高生育群体的自然增长率,即β (1B) b2 <0 将S=-b2I/b1代入g1(S,I)=0,易解得 为(6)式定义的侵入指数.显然,在假设(JS1)和(1B)下,系统(2)正平衡点E∗=(S∗,I∗)存在的充要条件为R>1.下面分析系统(2)在E0和E∗处的稳定性情况. 系统(2)的Jacobian矩阵为 对于平衡点E0=(0,0),有=J(0,0)=diag(b1,b2).又b1>0,b2<0,易得如下定理. 定理2系统(2)的零平衡点E0=(0,0)恒存在,且是不稳定的鞍点. 若生育观念侵入指数R>1,则正平衡点E∗=(S∗,I∗)存在.对于正平衡点E∗,有 设JE∗的两个特征值分别为λ1和λ2,有 可见在正平衡点E∗存在的条件下,JE∗的两个特征值为一对纯虚根.E∗是一个中心.下面定理进一步表明E∗的全局性态. 定理3当低生育群体的自然增长率b2<0时,若生育观念侵入指数R>1,则系统(2)的正平衡点E∗=(S∗,I∗)存在,且是一个全局中心,即除(S∗,I∗) 外的所有轨线都是包含(S∗,I∗)的周期轨. 为证明此结论,先证明下面两个命题. 命题1假设R>1,任取一从(S∗,I0) (I0 图3 b2 <0, R >1时系统(2)的等倾线及轨线走向示意图 最终p(x)=0在区间(-I0,I∗-I0)内有唯一解x=0,即p(I1-I0)=0当且仅当I1=I0时成立.证毕. 命题2假设R>1,则从区域I出发的轨线必与等倾线LS相交进入区域II,如图3所示.这里LS的表达式为 证一方面,若轨线不离开区域I,则它将保持在LS下方,此时I/S必有上界. 则易得limt→∞I/S=∞,进而与I/S有界矛盾.下证(11)式成立. 对任意z>S∗,记Gz={(S,I):S>z,I 下面证明定理3. 证设I0 ①进入区域III 然后趋向于(S∗,I∗),如图4 (a). 图4 b2 <0, R >1时系统(2)的等倾线及轨线走向示意图(a) 经区域III然后趋向于(S∗,I∗) (b) 经区域III和IV进入区域I,然后趋向于(S∗,I∗) ②经区域III 和IV 进入区域I,然后趋向于(S∗,I∗),如图4 (b). ③经区域III 和IV 进入区域I,然后交S=S∗于I1.由命题1 知,I1=I0,即Γ为一周期轨. 下说明情况①和②不成立. 这里α=β(kb1)-1.由命题1的分析知,(12)式成立当且仅当I∗-I0=0.这与I0 至此得,所有与线段M={(S∗,I) :I ∈(0,I∗)}相交的轨线必是周期轨.由命题1和命题2,从任意点出发的轨线如果不与M相交,则必趋向于(S∗,I∗).那么它必交于从(S∗,I0)(I0 下面考虑生育观念侵入指数R<1时,系统的动力学行为.有如下结论. 定理4当低生育群体的自然增长率b2<0时,若β<-kb2+kb1,即生育观念的侵入指数R<1,则低生育群体到高生育群体的生育观念侵入不成功.具体为 (i) 若β<-kb2,则I(t)→0,S(t)→N(t)→∞,t →∞,即若生育观念的传染力度无法抵消低生育群体的人口减少时,低生育群体人口数量将趋向于0,高生育群体人口数量将趋向于总人口数量且最终以Malthus 增长指数b1进行指数增长; (ii) 若β=-kb2,则I(t)≤I(0),S(t)→N(t)→∞,t →∞,即若生育观念的传染力度恰好抵消低生育群体的人口减少时,低生育群体人口数量将不再增加,高生育群体人口数量将趋向于总人口数量且最终以Malthus 增长指数b1进行指数增长; (iii) 若β>-kb2,但β<-kb2+kb1,则 即若生育观念的传染力度能够抵消低生育群体的人口减少速度但其余力不足以影响高生育群体的出生率时,低生育群体和高生育群体人口数量最终将分别以Malthus 增长指数b2+β/k和b1进行指数增长,低生育群体的人口增长速度将缓于高生育群体,生育观念侵入不成功. 即S(t)→∞,t →∞.从而N →∞且v=I/N →0,t →∞,由(5)式易得结论成立. (ii)β=-kb2.对任意初值(S(0),I(0))>0,由系统(2) 知≤I(b2+β/k),即I(t)≤I(0)对所有t ≥0 成立.进而有 下证S(t)→∞,t →0. 知I(t)→0,t →∞.从而易得S(t)→∞,t →0.故在β=-kb2时,有N →∞且v=I/N→0,t →∞,由(5)式立得结论成立. (iii)β>-kb2.下面将分三种情况说明S(t)→∞,t →∞. (iii-a) 若β 知,S(t)→∞,t →∞成立. (iii-b) 若β=kb1,则系统(2)的两条等倾线分别为I轴和 如图5 (a)所示.易知系统(2)只有唯一的零平衡点,且无闭轨.由于(0,0)是以I轴为稳定流形的鞍点,故没有轨线趋于(0,0).由Poincare-Bendixson定理[25,26],所有轨线必无界.而区域II中有<0,故区域II中所有轨线必会随S增加穿过LI进去区域I.在区域I中,有I<-S(β+kb2)/(kb2)-1/k.故从区域区I出发的解满足 图5 b2 <0, R <1时系统(2)的等倾线及轨线走向示意图(a) 无内部平衡点,区域II的轨线均进入区域I (b) 无内部平衡点,区域III和区域II的轨线均进入区域I 图6 系统(20)的等倾线及轨线走向示意图 图7 b2 <0,>1时系统(24)的等倾线及轨线走向示意图 从而有S(t)→∞,t →∞. (iii-c) 若β>kb1但β<-kb2+kb1,则系统(2)两等倾线分别为 如图5 (b).同(iii-b)的分析,从区域II和区域III出发的轨线必进入区域I,从而最终有S(t)→∞,t →∞成立. 故β>-kb2时,均有S(t)→∞,t →∞.进而有N →∞且v=I/N →0,t →∞,由(5)式易得结论成立. 注4在b2<0时,若生育观念的传染力度在抵消低生育群体的人口减少速度后其余力仍与高生育群体的自然增长率相当,即β=-kb2+kb1时,则R=1,理论上无法证得低生育群体到高生育群体的生育观念侵入情况.但第四节数值例子表明,此种情况下,低生育群体和高生育群体的人口数量最终将以相同的Malthus 增长指数进行增长,见图12.此时,发生不完全的生育观念侵入. 此时,在条件(JS1)下研究模型(1)的动力学行为,并分析这些动力学行为所蕴含的实际意义. (2A) b2 >0 令v=I/N,显然0≤v ≤1.此时u=S/N=1-v.类似(C1-B)的分析易知 从而,有如下结论. 定理5在国家采取鼓励生育政策下,即a>0,若低生育群体自然增长率b2>0,则当生育观念侵入指数Ra ≤1时,低生育群体对高生育群体的的生育观念侵入不成功,低生育群体和高生育群体的人口数量最终将分别以Malthus增长指数b2-a+β/k和b1进行指数增长.而当生育观念侵入指数Ra>1时,低生育群体到高生育群体有生育观念侵入,但不能完全同化高生育群体,即发生生育观念的不完全侵入.随着时间增大,低生育和高生育群体人口数量将以比例:a达到平衡并都指数增长,其最终的指数增量率均为 注5定理5表明,在国家采取鼓励生育政策下,不会出现低生育群体的生育观念完全侵入高生育群体的情形,即v →1,t →∞的情形. 注6由生育观念侵入指数Ra的表达式 及定理5可知,国家鼓励生育政策的力度a的大小直接影响到生育观念是否能够侵入.在参数β,k,b1,b2固定的情况下,国家鼓励生育政策的力度越大,即a越大,越不易发生低生育群体到高生育群体的生育观念侵入. (2B) b2=0 此时系统(1)变为 由(19)中I的方程易知,β/k与a的大小关系将决定I群体的人口数量.类似定理4的分析: 当β 当β=ka时,有I(t)≤I(0),S(t)→N(t)→∞,t →∞,从而v=I/N →0,t →∞; 当β>ka时,考虑辅助系统 这里N=S+I.该系统的两条等倾线为 定理6当低生育群体的自然增长率b2=0时,低生育群体到高生育群体的生育观念侵入不成功.具体为 (i) 若a>β/k,则I(t)→0,S(t)→N(t)→∞,t →∞,即若国家鼓励生育政策的力度大于生育观念的传染力度时,低生育群体人口数量将趋向于0,高生育群体人口数量将趋向于总人口数量且最终以Malthus 增长指数b1进行指数增长; (ii) 若a=β/k,则I(t)≤I(0),S(t)→N(t)→∞,t →∞,即若国家鼓励生育政策的力度恰好与生育观念的传染力度相当时,低生育群体人口数量将不再增加,高生育群体人口数量将趋向于总人口数量且最终以Malthus增长指数b1进行指数增长; (iii) 若a<β/k.进一步,若a ≥β/k-b1,此时≥0,则 即若国家鼓励生育政策的力度不小于低生育群体的生育观念对高生育群体自然增长率的影响力度时,低生育群体和高生育群体人口数量最终将分别以Malthus增长指数-a+β/k和b1进行指数增长. 若a<β/k-b1,此时<0,则 即若国家鼓励生育政策的力度未能弥补低生育群体的生育观念对高生育群体自然增长率的影响时,低生育群体和高生育群体人口数量最终将以相同的Malthus增长指数-ab1/(-a)进行指数增长,其人口数量比例稳定在:a. (2C) b2 <0 当b2<0时,系统(1)的非零平衡点为 系统(1)的Jacobian矩阵为 必有λ1<0,λ2<0,从而有如下定理. 基于N=S+I,考虑辅助系统 命题3系统(24)无周期轨. 这里α=-b1/b2.下寻找(25)中不等式成立的条件. 证一方面,若轨线不离开区域I,则它将保持在LN下方,此时I/N必有上界. 则易得limt→∞I/N=∞,进而与I/N有界矛盾.下证(26)式成立. 基于命题3-命题5,可证明如下结论. 由命题6,易得系统(1)正平衡点的全局稳定性. 定理10当低生育群体的自然增长率b2<0时,若a ≥β/k+b2-b1-b1(β/k/(b1-b2)-1),即≤1,则 (i) 若a>β/k+b2,则I(t)→0,S(t)→N(t)→∞,t →∞,即国家鼓励生育政策的力度大于生育观念的传染力度与低生育群体的人口增长速度之和时,低生育群体人口数量将趋向于0,高生育群体人口数量将趋向于总人口数量且最终以Malthus增长指数b1进行指数增长,此时低生育群体到高生育群体的生育观念侵入不成功; (ii) 若a=β/k+b2,则I(t)≤I(0),S(t)→N(t)→∞,t →∞,即国家鼓励生育政策的力度与生育观念的传染力度和低生育群体的人口增长速度之和相当时,低生育群体人口数量将不再增加,高生育群体人口数量将趋向于总人口数量且最终以Malthus增长指数b1进行指数增长,此时低生育群体到高生育群体的生育观念侵入不成功; (iii) 若a<β/k+b2.进一步,若a ≥β/k+b2-b1,此时≥0,则 即若国家鼓励生育政策的力度虽不及生育观念的传染力度与低生育群体的人口增长速度之和但足以弥补他们对高生育群体出生率的影响时,低生育群体和高生育群体人口数量最终将分别以Malthus增长指数b2-a+β/k和b1进行指数增长,此时低生育群体到高生育群体的生育观念侵入不成功; 若a<β/k+b2-b1但a ≥β/k+b2-b1-b1(β/k/(b1-b2)-1),此时<0时,则 即若国家鼓励生育政策的力度未能弥补生育观念的传染力度与低生育群体的人口增长速度之和对高生育群体出生率的影响时,低生育群体和高生育群体人口数量最终将以相同的Malthus增长指数(-ab1+)/(-a)进行指数增长,其人口数量比例稳定在:a,此时会发生低生育群体到高生育群体的生育观念的不完全侵入. 证结论(i)和(ii)的证明完全类似于定理4中结论(i)和(ii)的证明.结论(iii)的证明需要辅助方程 其轨线走向如图8.类似定理4 中(iii)的证明即可得本定理结论(iii). 图8 b2 <0, ≤1时系统(28)的等倾线及轨线走向示意图 综合定理9和定理10,可得如下结论. 定理11当生育观念侵入指数Ra>1时,定理9和定理10 (iii)的第二部分说明将发生低生育群体到高生育群体的不完全生育观念侵入;而当生育观念侵入指数Ra ≤1时,定理10的(i),(ii)和(iii)的第一部分说明低生育群体到高生育群体的生育观念侵入不成功. 本节通过数值例子验证结论的正确性,并讨论未能理论证得确切结论的注释.例子中,取定人口年净增长率b1=0.006,b2=0.001,0,-0.002 (数据来源参考于图1),取定k=1.传染系数β的值取自于0.001∼0.02,国家鼓励政策a的值取自于0.0005∼0.012(数据取值范围参考了人口净增长率,无确切参考文献).初值取定为(S(0),I(0))=(4,1)[3-4].人口数量单位为“亿”,时间长度单位为“年”.图9-图12为无国家鼓励生育政策(a=0)时,传染系数β的变化对低生育群体的生育观念对高生育群体能否(完全)侵入的影响;图13-图16为传染系数β=0.01取定时,国家鼓励生育政策的力度a的变化对低生育群体的生育观念对高生育群体能否侵入的影响. 图9 (a) 对定理1的例证, b2=0.001时, I/N在不同β下的时间序列图(b) 对注2 的例证, b2=0.001, R=1时,I/N趋向于一定值约为0.1725 (c) 对注3 的讨论, b2=0时, I/N的最终规模(I(T)/N(T))随β的变化趋势(d) 对注3 的讨论, b2=0, R=1时, I/N趋向于一定值约为0.167 图9 (a)为对定理1的例证.在低生育群体自然增长率b2=0.001>0下,由(6)中生育观念侵入指数的定义知,当β取值0.002,0.007,0.01时,R值分别为0.25,1.4,2.由图可见,R>1时,低生育群体到高生育群体的生育观念侵入成功,R<1时,生育观念的侵入不成功.而当β=0.005即R=1时,图9 (b)显示I/N将趋向于一定值约为0.1725,故此时会发生不完全的生育观念侵入.图9 (c),(d)为对注3的讨论.由图9 (c)可见,在低生育群体自然增长率b2=0时,若传染系数β 定理3表明,当低生育群体的自然增长率为负值时,系统(2)在生育观念侵入指数R>1下将存在唯一全局中心.取定低生育群体的自然增长率b2=-0.002,由文化规范侵入指数的表达式知β=Rk(b1-b2),进而有β>0.008⇔R>1,β=0.008⇔R=1,β<0.008⇔R<1.图10例证了传染系数β=0.012时(此时,R=1.5>1),三个不同初值下,系统(2)存在一个全局中心(S∗,I∗)=(0.5,1.5).图11例证了生育观念侵入指数R<1时,生育观念侵入不成功.图12例证了生育观念侵入指数R=1时,低生育群体和高生育群体的人口数量比值将趋向于一具体数值,即具有相同的Malthus增长指数.所以在低生育群体自然增长率b2<0且生育观念侵入指数R=1时,生育观念侵入成功但不能完全侵入. 图10 对定理3的例证, b2= -0.002且R >1时,三个不同初值下系统(2)存在唯一正平衡点(S∗,I∗),且是一个全局中心(a) S, I周期变化的时间序列图(b) S, I周期变化的相图 图12 对注4的讨论, b2= -0.002且R=1时,三种不同初值下S, I随时间变化的时间序列图(a)和I/S随时间变化的时间序列图(b),由图可知,生育观念侵入成功但不能完全侵入 取定传染系数β=0.01,下面例证在有国家鼓励生育政策下,鼓励生育政策力度a的大小对生育观念能否侵入的影响. 若低生育群体的自然增长率b2=0.001>0,那么鼓励生育政策的力度a ≥0.005可保证生育观念的侵入指数 此时低生育群体到高生育群体的生育观念侵入不成功,如图13 (a)和(b).但若鼓励生育政策的力度不够,即若a<0.005,此时将有R>1,则会发生生育观念的侵入.由于有国家鼓励生育政策的存在,不会发生完全的生育观念侵入.随着时间的增大,低生育和高生育群体的人口数量最终将以比例4:1 (a=0.001)和1:4 (a=0.004)达到平衡并以相同的Malthus增长指数进行指数增长,两种情况下的指数增长率分别为0.002和0.005,如图13 (c)和(d).图13表明,国家鼓励生育政策的力度越大,越不易发生低生育群体到高生育群体的生育观念侵入.当其他参数有确切数值时,可计算出国家鼓励生育政策力度的参考值,从而可更合理的制定国家的鼓励生育政策. 图13 对定理5的例证, b2=0.001,(a)和(b)分别为Ra ≤1时S, I及I/S的时间序列图,(c)和(d)分别为Ra >1时S, I及I/S的时间序列图,由图可见, Ra ≤1时生育观念的侵入不成功;而Ra >1时发生不完全的生育观念侵入 若低生育群体的自然增长率b2=0,则鼓励生育政策力度的阈值a=0.004.当a ≥0.004时有Ra ≤1,此时低生育群体到高生育群体的生育观念侵入不成功,如图14 (a)和(b).但若a<0.004,则会发生生育观念的不完全侵入,如图14 (c)和(d). 图14 对定理6的例证,(a)和(b)分别为不发生生育观念侵入时S, I及I/S的时间序列图,(c)和(d)分别为发生生育观念侵入但不完全时S, I及I/S的时间序列图 在低生育群体的自然增长率b2=-0.002<0下,若国家采取鼓励生育政策的力度不够,即 此时,发生低生育群体到高生育群体的不完全生育观念侵入.若a=0.0001,则低和高生育群体的人口数量最终将稳定在(1.3125,3.9375)处,如图15.若国家加大鼓励生育政策的力度但仍未能弥补生育观念的传染力度与低生育群体的人口增长速度之和对高生育群体出生率的影响即a<β/k+b2-b1=0.002 时,则会发生不完全的生育观念侵入.随着时间的增大,低生育和高生育群体的人口数量最终将以比例3 :1 (a=0.0005),1 :1 (a=0.001)和1 :3 (a=0.0015)达到平衡并以相同的Malthus 增长指数进行指数增长,三种情况下的指数增长率分别为4.2352×10-19,0.002和0.004,如图16 (a)和(b).但若国家鼓励生育政策的力度足以弥补文化规范的传染力度与低生育群体的人口增长速度之和对高生育群体出生率的影响时,即a ≥0.002时,低生育群体到高生育群体的生育观念侵入不成功,如图16 (c)和(d). 图15 对定理9的例证,当国家鼓励生育政策的力度a=0.0001时,系统(1)存在唯一正平衡点(1.3125,3.9375)且是全局渐近稳定的,(a)和(b)分别为两组初值下S, I的时间序列和相图 图16 对定理10的例证,(a)和(b)分别为发生不完全生育观念侵入时S, I及I/S的时间序列图,(c)和(d)分别为生育观念侵入不成功时S, I及I/S的时间序列图 低生育率在我国某些地区已表现的非常明显,对生育观念在个体间传播的研究也就非常有必要.本文考虑包括生育观念在内的导致低生育率的更广义的生育观念,借助传染病模型的思想,建立了一类简单的人口转型中生育观念的传播模型,给出了生育观念是否传播的充分必要条件.具体为,在无国家鼓励生育政策时,定义出生育观念侵入指数R=β/(k(b1-b2)),理论证得当R<1时,低生育群体到高生育群体的文化规范侵入不成功;当R>1 且低生育群体的自然增长率b2>0时,发生完全的生育观念侵入,b2<0 时,发生不完全的生育观念侵入.数值实验例证了当R>1且b2=0时,发生完全的生育观念侵入;R=1时,对任意的低生育群体自然增长率b2均发生不完全的生育观念侵入.在有国家鼓励生育政策时,给出生育观念侵入指数Ra=β/(k(b1-b2+a)),理论证得当Ra ≤1 时,低生育群体到高生育群体的生育观念侵入不成功;当Ra>1时,发生不完全的生育观念侵入. 本文所建立的生育观念模型较简单,从理论证明和数值例证两方面全面的讨论了系数不同取值时模型的各种动力学行为.鉴于部分特殊情况未理论证明出结果,只是通过数值例子进行了讨论,如注2-注4,故模型的完全理论讨论是我们需要努力之处.同时,在本文模型基础上,还有许多思考值得进一步的深入研究. 1.本文考虑全国人口中生育观念的传播模型,忽略了出国与归国的人口流动.若考虑国内具体地区,则人口流动的因素不可避免,可针对具体地区考虑具有人口流动的生育观念传播模型. 2.本文只考虑了生育观念的传播结果,并未考虑其传播方式,如生育观念的垂直传播,水平传播和倾斜传播[27-28].传播方式的不同会影响传播系数的变化,可细分传播方式进行更细致的建模研究. 3.本文假设了固定的常数传播系数,而个体内在价值观的改变,社会生育,养育成本的增加等等因素会影响传播强度[9-10],可根据实际影响传播强度因素的不同考虑变系数的生育观念传播模型. 4.本文只考虑了生育观念的传播对人口数量的影响,而众多对人口转型问题的研究都考虑其与经济增长,教育进步,技术进步,农业向工业化转变,消费习惯,储蓄率等的关系[3,4,6,8-10],故可考虑从不同角度融入相关因素的较复杂的生育观念传播模型. 5.本文考虑低生育和高生育两群体总人口的变化情况,但不能准确反应适龄群体人口数量.人口的老龄化,适龄生育群体年龄范围的增大等现象与人口的年龄结构密切相关[21],考虑具有年龄结构的生育观念传播模型具有明显的现实意义.




3.2 有国家生育政策干预(a >0)

§4 数值例子






§5 结论
