基于区域分块的PCB图像配准算法研究
2023-12-13陈建华徐雷郭战岭牟宗亮
陈建华, 徐雷, 郭战岭, 牟宗亮
(四川大学, 机械工程学院, 四川, 成都 610065)
0 引言
PCB作为现代电子信息产品中不可或缺的电子元器件,广泛应用于计算机、消费电子、网络通信、医疗、汽车电子、航空航天科技等领域[1]。特别是近年来,5G技术已经投入商用,行业规模不断扩大,对PCB产品质量检测的要求也越来越高。因此PCB自动光学检测设备(AOI)逐渐取代低效率的人目检[2-3],在利用AOI设备进行PCB缺陷检测前,必须将方位存在偏差和旋转的待测图像与PCB模板图配准[4]。常用的PCB图像方位配准方法有Mark点检测、PCB边缘检测、角点检测等[5-6]。目前,常用的2种方法是基于图像边缘和图像灰度的特征点提取。使用提取图像边缘获得的结果往往取决于边缘的清晰程度,效率低,且时间成本高。角点检测主要通过计算点的曲率和梯度来检测角点,避免了上述缺陷。目前,相关算法主要有SIFT算法、SURF算法和ORB算法。与SIFT算法和SURF算法相比,它具有检测速度非常快、旋转不变性等优点,但另一方面也存在特征提取精度低、不具备尺度不变性的缺陷。杨倩兰等[7]通过融合SURF算法以及引入极线约束的方式解决了ORB算法不具备尺度不变性的问题;张磊等[8]通过自适应频谱抑制的方式解决ORB算法提取特征点不稳定的问题;丁进选等[9]采用空间一致性的思想优化了ORB算法不具有尺度不变性的问题。然而,ORB算法的缺点在于特征提取比较集中、匹配精度较差。针对这个问题,需要采用其他的算法来优化特征提取结果,使得特征提取更加均匀。
1 ORB算法简介
ORB算法由2部分组成:关键点和描述子。其中,关键点被称为“Oriented FAST”,是在FAST算法基础上的改良版。
1.1 Oriented FAST特征点提取
FAST检测特征点的原理可以简单概括为对于图像中任意1个特征点P,如果在其周围存在足够多的点与P的像素差值达到指定的阈值,则这个点P可以被视作1个特征点。
FAST算法检测特征点的具体步骤如图1所示。
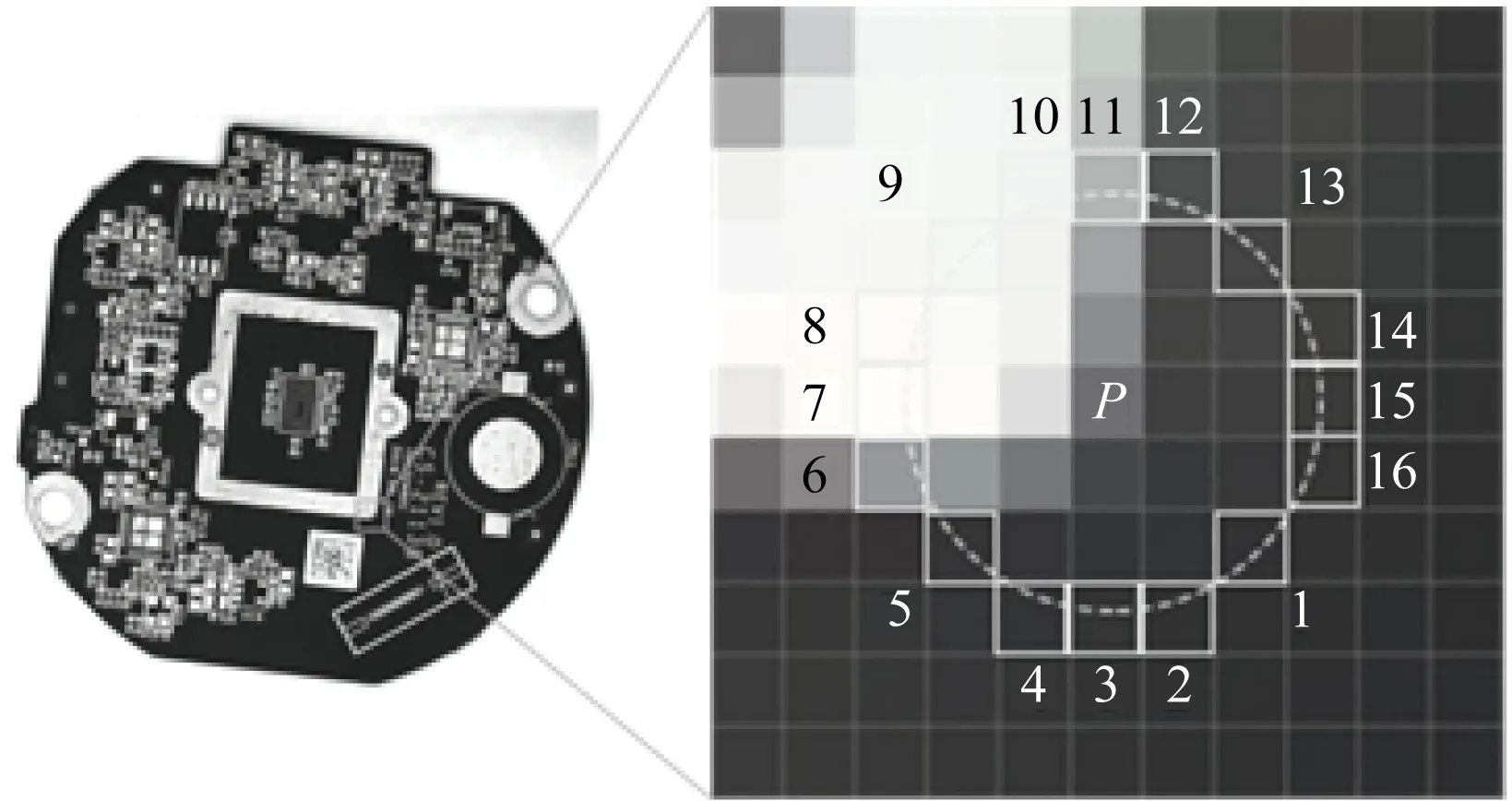
图1 FSAT算法特征检测原理
(1) 图1中,P代表图像中的任意一点,以P点为圆心,3个像素为半径作一个圆,由图1可知,圆上共有16个像素点。
(2) 分别计算16个像素点与P点灰度值差值的绝对值a1、a2,…,a16。
(3) 设定一个阈值t,将a1、a2,…,a16与t比较,若ai>t(i=1,2,…,16),则认为这是2个不同的点。
(4) 若16个像素点中至少有n(n通常取9、11或12)个点与点P不同,则认为P点为一个特征点;反之,P点不为特征点。
(5) 重复以上操作,对图像中每一个像素点都进行以上过程。
以上过程提取出的特征点只有位置信息,并没有方向信息,因此原始的FAST算法提取出的特征点不具有旋转不变性。针对此问题,ORB算法采用灰度质心法解决,使得检测出的特征点具有方向信息。
其步骤如下:
(1) 在一个小的图像块K中,将图像块的矩定义为
(1)
其中,p,q={0,1},I表示点(x,y)的灰度值。
(2) 通过式(1)计算出的矩,可以进一步得到图像块的质心C:
(2)
(3) 若记图像块M的几何中心为点O,则连接OC可以得到一个方向向量,因此提取出的特征点p(x,y)的方向可以定义为
(3)
1.2 BRIEF描述子
使用O-FAST算法得到一系列特征点后,需要使用某种方式定义每个特征点的属性,使得每个特征点之间有差异,对后续的点对匹配有利。这些属性的输出结果则称为描述子,ORB算法采用BRIEF算法来计算某个特征点P的描述子,其核心思想在于:在特征点P的附近以某种模式选取n个点对,把这n个点对相互之间的比较结果组合起来即作为点P的描述子。
BRIEF算法的操作步骤如下。
(1) 以特征点P为圆心,d为半径作圆O。
(2) 在圆O内以某种模式选取n个特征点对,以n=6为例,将选取的6个点对分别记作:P(A1,B1),P(A2,B2),P(A3,B3),P(A4,B4),P(A5,B5),P(A6,B6)。
(3) 定义操作一个运算方式T。
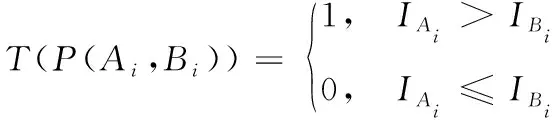
(4)
其中,IAi、IBi分别表示点Ai、Bi的灰度值,i=1,2,…,6。
(4) 使用T运算分别对6对特征点进行操作,并且将得到的6个结果进行整合。
例如:
T(P(A1,B1))=1,T(P(A2,B2))=0,T(P(A3,B3))=1,T(P(A4,B4))=1,T(P(A5,B5))=0,T(P(A6,B6))=1,则点P的描述子即为101101。
2 基于区域分块的改进ORB算法
传统的ORB算法由于采用FAST算法来提取特征点,导致提取出的特征点往往会集中在某一点,导致后续特征匹配过程产生大量的误匹配。
本文使用图像分块与ORB算法结合的方式提取分布均匀的特征点;然后对提取出的特征点使用Hamming距离粗筛选以及RANSAC算法进行精筛选;最后利用RANSAC算法计算出2幅图像之间的单应性变换矩阵,对2幅PCB图像进行配准。算法整体的流程如图2所示。
2.1 区域分块及特征提取
ORB采用FAST算法提取特征点,其优点是速度非常快,但是提取出的特征点往往非常集中,计算出的描述子会十分相似,在进行PCB图像配准时便会产生大量的误匹配点。因此本文针对ORB算法提取PCB特征点冗余集中的问题,提出一种区域分块方法,通过控制每小块图像可提取的特征点数目,达到提取分布均匀的特征点的目的。
区域分块算法流程如图3所示。

图3 区域分块算法流程
图像分块的具体步骤如下。
(1) 导入2幅图像,将2幅图像各均匀划分为R*C小块。其中,R代表行数,C代表列数。初始取R=2,C=2。
(2) 设定每张PCB图像中共需要提取的特征点数目为T,取T=500。
(3) 设定阈值j,j=T/(R*C),初始j=125。
(4) 使用ORB算法在R*C个区域中分别提取特征点。
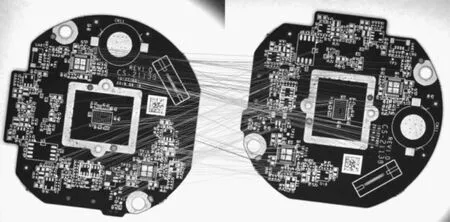
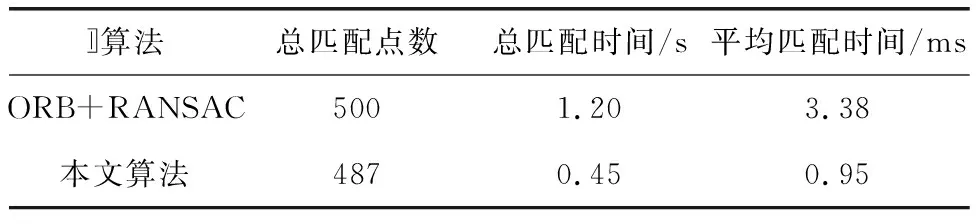
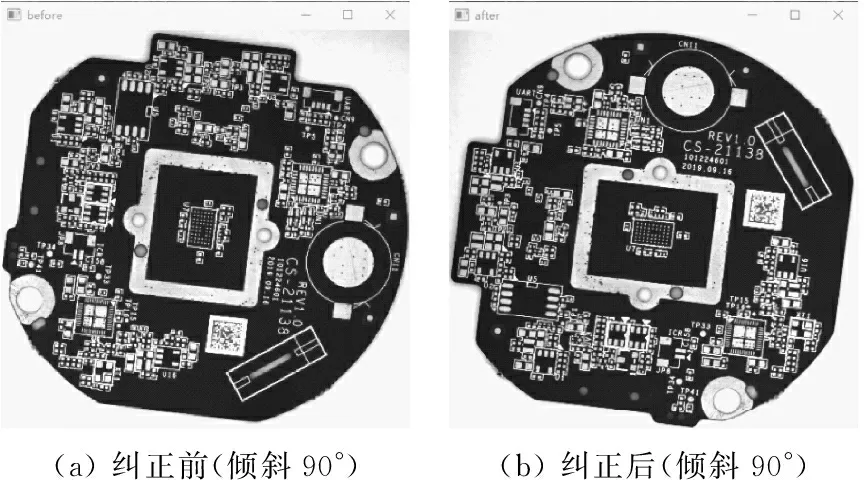
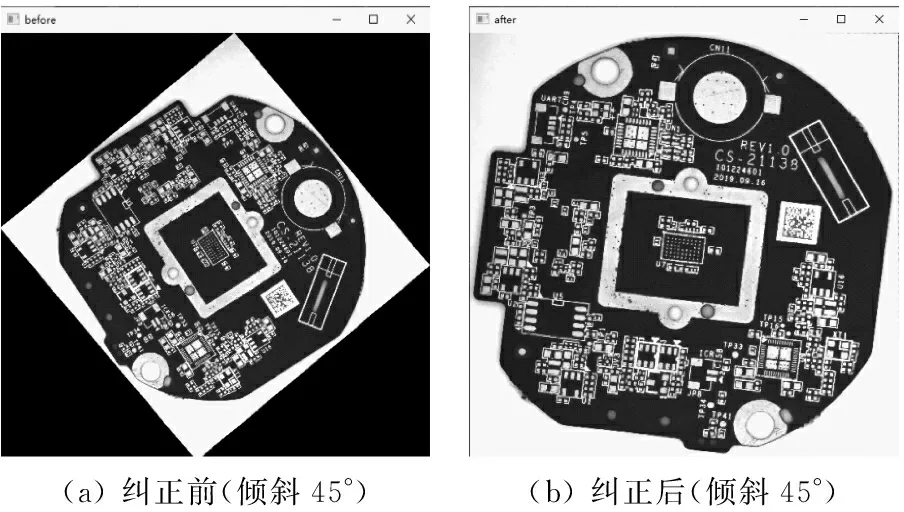
(5) 将各小块图像提取的特征点数量与j比较:若数量 (6) 对R*C各区域进行遍历,若每个区域剩余的特征点数量等于j,则停止特征点提取操作。 (7) 将分块后的图像重新拼接,以方便后续PCB配准。 通过以上步骤提取出足够的特征点后,需要将待配准图像(记为M1)与模板图像(记为M2)的特征点进行匹配。同时采取汉明距离对M1和M22幅图像进行特征点的粗匹配,筛选掉误差较大的特征点,但传统的ORB算法仍然达不到高精度的要求。因此,本文使用RANSAC算法对粗筛选之后的特征点对进行进一步精确筛选,使得最后留下的均为没有误差或者误差较小的特征点对。其运算流程如图4所示。 其伪代码如下: Begin Dim Q as integer‘定义粗筛选后特征点对 Dim D as integer‘定义内点数 Dim S as integer‘定义迭代步数 Input Q D=0 S=0 在Q中随机提取4对特征点,计算3阶矩阵模型H Return H S=1 If (S<=1000)And(other feature point pair satisfy H) Then D=D+1, S=S+1 Else Endif Return D, S If D>=Q*0.95 Then Endif Output D‘输出精确特征点 具体步骤如下。 (1) 利用汉明距离对提取出的500对特征点进行粗筛选,得到剩余特征点对数Q,输入Q对特征点。 (2) 由于M1和M2之间的变换矩阵H为3*3阶,而其中仅有8个未知参数,则对应需要4对特征点进行求解。因此,取K=4,从Q对特征点中随机抽取4对特征点。 (3) 利用抽取的4对特征点计算出一个3*3阶矩阵模型。 (4) 使用(3)中计算出的模型对其余特征点对进行估计,若其余特征点对在误差范围内满足模型,则属于内点,反之则属于外点。 (5) 设置一个迭代步数E,重复迭代,计算矩阵模型,最后取内点数目对应最多的矩阵H。 (6) 将矩阵H对应的外点筛选掉。 (7) 结束。 实验平台:软件为Win 10系统、Pycharm-Opencv 4.5;硬件为显示器DeLi、相机型号MARS-3140-3GM-P-M03。 实验对象:5 G PCB板。 本实验基于Win 10系统+Opencv 4.5的平台来进行,实验对象为5 G PCB板。PCB待配准图像及模板图像如图5所示。 图5 PCB待配准图像及模板图像 传统ORB算法与本文算法的特征提取及匹配图像结果如图6和图7所示。 图6 传统ORB算法匹配结果 图7 本文算法匹配结果 通过图6、图7对比可以明显看出:改进后的ORB算法相较于传统ORB算法提取出的特征点分布更加均匀,说明本文提出的图像分块特征提取思想有较好的结果;改进后的ORB算法在匹配时效果较好(误匹配对减少)。为避免实验的偶然性,本实验采取10次实验结果的平均值的方式进行统计。 改进前和改进后的PCB图像特征点匹配精度如表1所示。改进后的匹配精度提升了约26个百分点。 表1 匹配精度对比 改进前和改进后的PCB图像特征点匹配时间如表2所示。改进后的匹配时间提升了约255%。 表2 匹配时间对比 图8、图9为PCB待配准图像方位纠正前后例图。 图8 PCB待配准图像方位纠正前后例图 图9 PCB待配准图像方位纠正前后例图 由于ORB算法使用FAST算法检测特征点本身存在特征点冗余、密集的问题,本文尝试使用区域分块的方式,使得检测出的特征点强制分散,达到了提取均匀特征点的目的。通过实验结果得知,相较于改进之前的ORB算法,本文算法在配准精度和配准时间两方面都有所提升。2.2 特征匹配及筛选
3 实验结果及分析



4 总结
