基于Two-archive 2的电子产品多目标逆向物流网络优化
2023-12-13潘华贤
潘华贤
(西安财经大学行知学院, 经济与统计学院, 陕西, 西安 710038)
0 引言
在进行逆向物流网络的设计时,需考量成本、顾客满意度以及环境因素等多项优化目标[1],由此构成多目标优化问题。基于进化算法的多目标优化算法(MOEAs)已经成为解决多目标优化问题的主要途径。MOEA/D、NSGA-III等多目标优化算法在应用过程中出现如计算复杂度较高、无法平衡算法的收敛性与多样性等问题[2],而Two-archive 2 (TwoArch 2)算法可有效平衡这些问题[3]。为了降低能源消耗,本文将物流可持续发展与节能减排的全新理念进行有效衔接。
1 问题描述
本文考虑第三方回收下的电子产品回收逆向物流网络,如图1所示。该网络由回收站、回收中心、再制造工厂选址和节点之间的运输路径构成。
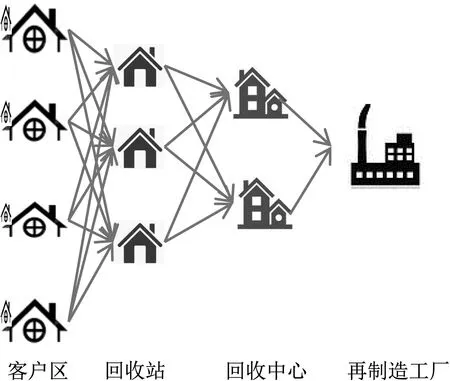
图1 电子产品回收逆向物流网络
本文所规划的逆向物流网络使得网络中的运营成本最小、顾客满意度最大(包括响应时间及覆盖率)、碳排放目标值最小[4]。为了建立模型,前提假设参见文献[5],并只考虑各个节点处理过程中和产品在运输过程中的碳排放。
2 模型的构建
2.1 模型参数与决策变量
本文所研究的模型主要针对电子产品从客户到回收中心单周期多目标逆向物流网络构建及优化问题,模型中的变量符号及含义描述如表1、表2所示。

表1 变量符号及含义

表2 决策变量及含义
2.2 目标函数
minf1=Cgh+Cph+Cyw+CThw
(1)
式(1)为最小化逆向物流总成本,包括回收站的年固定开设成本、产品在回收站的处理成本、回收中心的固定建设成本以及产品在回收站和回收中心之间往返的运输成本。
(1) 回收站年固定开设成本
(2)
(2) 产品在回收站的处理成本
(3)
(3) 回收中心的固定建设成本
(4)
(4) 产品在回收站与回收中心之间往返的运输成本
(5)

(6)
(7)
式(6)和式(7)中,p1、p2为运输量,q1、q2为回收站j到回收中心的运输距离。
(8)
式(8)为最小化顾客服务时间,即产品返修总时间,包括维修时间和产品在回收站和回收中心之间的运输时间[6]。
(9)
式(9)为最大化回收站对回收产品的服务覆盖率,即理想化回收站与客户的距离。式(8)与式(9)构成了衡量客户满意度的标准。
(10)
式(10)为最小化碳排放量,主要考虑回收中心运营过程中产生的碳排放以及这2个节点间运输过程中的碳排放。
(11)
式(11)确保1个顾客区域只能分配到1个回收站。
(12)
式(12)确保1个回收站只能分配到1个回收中心。
(13)
其中,M为一个随机选择的较大的正数,该约束能够确保顾客区域分配到回收站,防止被分配到未开放的回收站[7]。
(14)
式(14)确保开放的回收中心能够接收来自回收站的产品,避免回收站分配到未开放的回收中心。
(15)
该约束确保回收站接收的产品总量不超过回收中心的最大容量。
Xij,Yjk,Hj,HCk∈(0,1),TVjk≥0,∀i∈I,
∀j∈J,∀k∈K
(16)
其中,τ为设立回收站的最小数量,σ为设立回收中心的最小数量,确保开放的回收站和回收中心的数量不小于要求开设的最小数量。
3 Two-archive 2算法
研究发现,所建模的多目标优化问题极易出现收敛性与多样性等不平衡问题。为了解决该问题及降低复杂度,基于IBEA算法中的Iε+指标和帕累托支配,并受收敛性和多样性档案(CA和DA)的双档案算法(Two_Arch)的启发,对CA和DA分配不同的选择机制。对初始非支配解集划分为CA和DA,在CA和DA中执行交叉操作,在进化过程中在CA中执行变异操作。CA由IBEA算法中的评价指标进行更新,旨在引导种群迅速向PF收敛。DA的目的是在高维目标空间中增加种群的多样性。一旦DA的个体溢出,所采用的维护多样性的保护机制会进行截断。在CA对多样性作用程度较低的情况下,由于DA保持了多样性和收敛性的平衡,将使用DA作为最终输出。算法流程如图2所示。

图2 算法核心流程图
(1) 收敛性档案
CA的选择机制采用Iε+指标,表示在目标空间中解x1,支配解x2所需的最小距离:
Iε+(x1,x2)=minε(fi(x1)-ε≤fi(x2),1≤i≤m)
(17)

(2) 多样性档案
首先将边界点(具有最好和最差目标的解)输入DA,之后在每次迭代过程中选择出与已选解不同的解,将其添加到DA中,直到达到DA的容量上限。在评价解的多样性时,算法采用了Lp范数距离(p<1)。由于CA的多样性较差,因此将DA作为最终输出。
4 算例求解与分析
4.1 算例描述
本文所设计的物流系统共50个客户区,备选回收点20个,备选回收中心8个,假设回收站最小设立数量τ为5,建设回收中心的最小数量σ为1,年运营时间β为250天,回收中心k的年平均建设费用vk为3000,回收中心k的最大容量mk为2000。平均每件产品的处理时间tc为10,单位产品处理成本α为0.1,顾客期望的产品处理时间tq为30。单位产品在回收点和回收中心之间往返的运输时间tjk=djk×0.6,交通运输量p1为200,p2为400,运输距离惩罚比率δ1设定为1.1,δ2为1.2,运输距离q1为25,q2为60,单位产品标准运输成本E为1。其余模型参数值如表3所示。计算结果不受参数单位影响。

表3 模型参数
4.2 结果分析
将种群规模设定为100,最大评估次数设定为10 000,交叉率为90%,变异率为10%,以式(1)、式(8)、式(9)和式(10)为目标函数运行程序。
图3为随机选取的优化后的客户区与回收站的关系图,c2、c6、c9、c12、c14、c18表示优化出的回收站,黑色点及线条表示分配至相应回收站的客户区,而m2、m4、m5及其与回收站之间的线条表示回收站与回收中心的分配关系。例如,将c6和c12回收站分配至回收中心m4。

图3 客户区与回收站的分配关系
分别利用BiGE、NSGAIII、crEA、GrEA、TwoArch 2对优化模型进行求解,绘制最优解的平行坐标。由图4可知,所有都收敛到了真实的帕累托面,但分布存在差异性。虽然BiGE也收敛到了PF,但其多样性太差,大部分解分布在小区域内。crEA与TwoArch 2算法分布更加均匀,体现了良好的多样性。由于HyperVolume指标评价方法可综合评判多目标解集的收敛性、均匀性与广泛性,因此,图4对5种算法的HV值进行了对比。由图4可知:BiGE算法的值最小,与最大值相差0.05,性能最差;TwoArch 2得到了较高的HV值,NSGAIII算法次之,结合图3,表明TwoArch 2算法综合性能较其他算法较优。表4 为随机选取的6组Two-archive 2求解得到的帕累托解集。
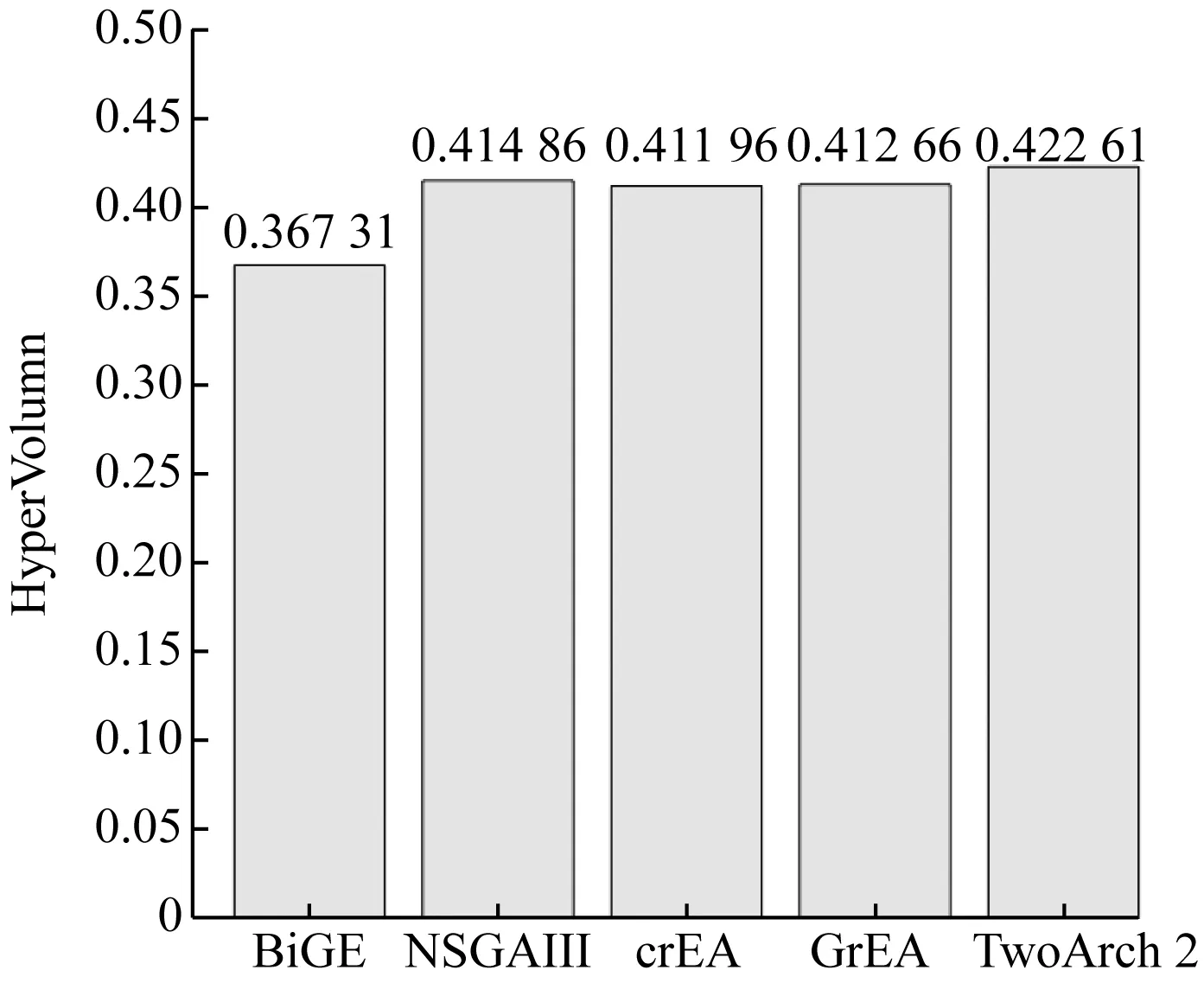
图4 HV实验结果对比

表4 Two-archive 2求解得到的帕累托解集
5 总结
采用改进双档案算法对模型进行求解,有效避免了收敛性与多样性不协调的问题,保障算法能够产生最优解。仿真结果表明,基于碳排放约束的逆向物流网络选址方案产生的固定费用较少,能够帮助企业降低成本以及综合考虑社会环境因素。
