基于混合整数规划的航班保障资源调度研究

2023-12-13康永汪福军沈光越

微型电脑应用 2023年11期

康永, 汪福军, 沈光越

(东部机场集团有限公司, 江苏, 南京 211106)

0 引言

航班保障过程中需要大量的特种车辆和保障人员,以国内某大型机场为例,高峰时段每天起降航班700多架次,航班保障车辆近500台,保障人员超过1000人,机场的保障效率会直接影响航班的准点率。因此,如何高效合理地调度各种航班保障资源,成为每个大中型机场迫切需要解决的问题。

很多机场采用传统资源调度模式,以纸笔记录方式实现任务分配,由于不同航班所需要的保障资源不同,以及个人工作效率和记忆能力的限制,随着航班量的增加,只能通过不断增加调度人员和调度层级来解决。信息技术的不断发展为改变传统调度模式提供了机遇,由于需要根据不同的航空公司、航班类型、飞机型号、机位性质、车辆类型、人员资质等条件进行分配,因而要求航班保障任务分配方法能够满足多种限制条件。同时,也需要充分考虑机场不断变化的航班起降时间以及航班保障车辆人员的动态位置和状态,避免出现航班保障任务遗漏的情况,因此需要分配方法能够根据实时的运行数据对结果快速进行重新计算和分配。

国内外学者从不同的角度对航班保障资源分配问题开展了大量的研究。冯明端等[1]通过遗传算法研究了机场地面特种设备车辆构建带有容量限制和时间窗的全种类车型车辆联合调度的约束模型,并与先到先服务算法相比,明显减少了车辆的使用数目和行驶距离。吴枕[2]根据机场保障车辆实际调度中的约束条件以及不同的需求建立了车辆动态协同调度模型,采用遗传算法对昆明长水国际机场车辆的实际运营数据进行挖掘,实验结果表明其算法在解决航班信息变化影响的问题时,能够很好地满足车辆动态调度的要求,降低车辆的运行成本。

混合整数规划模型是指部分决策变量限制为整数的规划问题,其经常被用来处理复杂网络选址、资源排班调度等可抽象为0和1选项的场景[3]。BAYLISS等[4]提出了一种混合整数规划方法来安排航空公司的后备机组人员,其目标是找到在一组输入情景中最小化总体中断水平的后备人员时间表。张红颖等[5]按照科学合理地权衡机场各种约束限制需求,提出了优化停机位调度问题的混合整数规划模型,目标是在确保航空器安全运行的前提下使得航班延误的总时间最短。根据以上研究可知,混合整数规划模型已应用在多种行业的资源调度上,但是在航班保障资源调度方面的应用少有研究。

1 模型建立

经与机场航班保障地面服务管理人员深入研究和探讨,梳理出机场航班保障资源管理中心整体流程,主要包括3个主要步骤:首先根据次日航班计划编排保障资源计划,并形成预排班表;其次根据航班运行情况,以特定规则进行最优化资源调度;最后由实际保障人员及时反馈任务接收和执行进度。具体流程如图1所示。

图1 机场资源管理中心业务流程

规划排班和调度管理是最重要的两个阶段。在规划排班阶段,需要根据航班的次日计划计算出次日需要的最少保障资源作为次日保障的最低人数,并输出次日排班表。调度管理阶段由于航班量巨大且实时变化,以人工方式很难做到最优调度,即使采用任务均衡规则也会因为特定航班特定服务而难以实现,同时为防止航班延误带来的资源分配风险,有时候可能会在最低资源基础上配置一定的冗余,由此需要根据实际资源重新分配保障任务,能够实现根据航班运行情况动态生成保障任务,并结合当前航班保障资源分布情况进行最优分配。综上建立模型:模型一,根据航班次日计划的起降时间,以获取最小分配资源数量作为目标,具备预留好人工休息时间等约束条件;模型二目标为根据航班实际运行情况,结合现有可分配人员和已分配任务等约束条件,以分配后总体效益最大值作为目标。

1.1 模型一

模型一核心目标为按照航班次日计划求解出所需最小航班保障资源数量以及相应的排班规则。根据航班计划推导出所有保障任务清单情况,按照任务类型和资源工作时间范围计算出所需最小资源数量和任务分配,其结果可作为次日排班计划的参考。

(1) 变量定义

模型一的变量定义见表1,这些变量用来描述模型的目标函数和约束条件,为方便计算,可以将时间类数据转化为整数类型,计算完成后再转为时间类型。

表1 模型一变量定义

(2) 目标函数

目标函数是获取所有空余时间最短,即用所有资源工作时间的总工时减去完成所有任务所需要的总工时,其函数如下:

(1)

其中,所有资源工作时间的总工时,用所有资源工作时间的和减去休息时间与已接收任务时间的和:

(2)

完成所有任务所需要的总工时的计算公式为

(3)

(3) 约束条件

约束条件如式(4)～式(9):

xrp∈{0,1}∀r∈R,p∈P

(4)

(5)

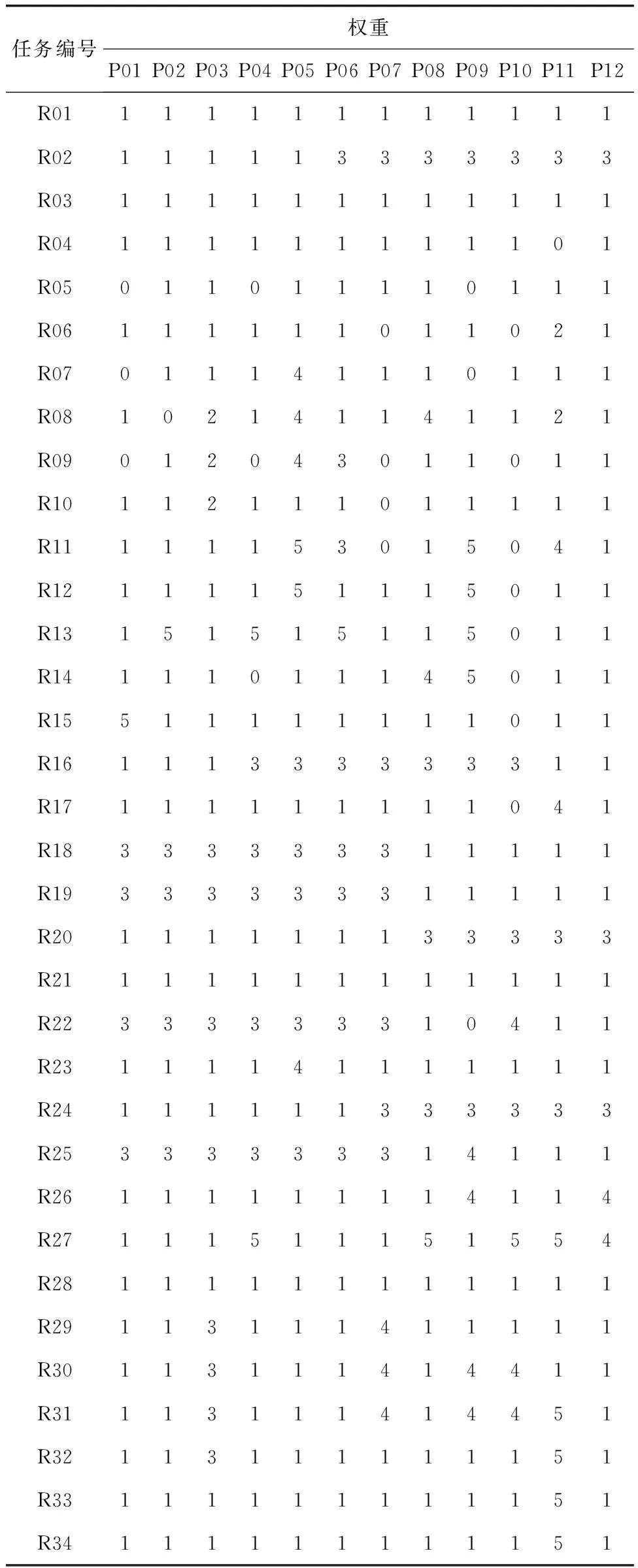
PBp

∀r∈R,p∈P,xrp≠0

(6)

∀r∈R,p∈P,xrp≠0

(7)

∀r∈R,p∈P,xrp≠0

(8)

∀r∈R,r′∈R,p∈P,r≠r′,xrp≠0

(9)

式(4)表示保障任务被分配情况,为1时表示任务r被分配给资源p,否则为0。式(5)表示每个保障任务必须被分配,且只能分配1次。式(6)表示分配给同一资源的所有任务的开始时间和结束时间均要求在工作时间范围内。式(7)、式(8)表示所有待分配给同一资源的任务的开始时间和结束时间不能落在休息时间的区间内,休息时间的开始时间和结束时间也不可落在待分配任务的时间区间内,须确保各时间区间相互独立,以此防止需要分配的任务和休息时间产生冲突[6]。式(9)表示所有待分配给同一资源的任务的开始时间和结束时间不能落在其他待分配任务区间,以防止待分配任务间的时间冲突。

1.2 模型二

由于不同航班所需保障要求不尽相同,比如某些特殊服务航班需要安排工作经验丰富的保障资源,因此不同航班对资源保障的期望值不同,模型二核心目标为按照航班当日执行情况快速地解出资源分配方案。要求模型二能够根据不断变化的航班执行情况实时推导出所有保障任务清单情况,按照任务类型、可用资源清单、资源空余工作时间、资源与任务匹配程度等条件快速计算出最优化分配策略。

(1) 变量定义

模型二的变量定义见表2,这些变量用来描述模型的目标函数和约束条件。

表2 模型二变量定义

(2) 目标函数

目标函数为获取所有任务分配后的最大权值总和,如式(10):

(10)

(3) 约束条件

约束条件如式(11)～式(17):

xrp∈{0,1}∀r∈R,p∈P

(11)

(12)

PBp

∀r∈R,p∈P,xrp≠0,Qrp>0

(13)

∀r∈R,p∈P,i∈I,xrp≠0,Qrp>0

(14)

∀r∈R,p∈P,i∈I,xrp≠0,Qrp>0

(15)

∀r∈R,r′∈R,p∈P,

r≠r′,xrp≠0,Qrp>0

(16)

(17)

式(11)表示保障任务被分配情况,为1时表示任务r被分配给资源p,否则为0。式(12)表示每个保障任务必须被分配,且只能分配1次。式(13)表示分配给同一资源的所有任务满足权值不为0,并且开始时间和结束时间均要求在资源的工作时间范围内。式(14)、式(15)表示所有待分配给同一资源的任务满足权值不为0,并且开始时间和结束时间不能落在资源已接收任务或休息时间的区间内,已接收任务或休息时间也不可落在待分配任务的时间区间内,以此防止需要分配的任务和休息时间产生冲突。式(16)表示所有待分配给同一资源的任务满足权值不为0,并且开始时间和结束时间不能落在其他待分配任务区间,以防止待分配任务的时间冲突。式(17)表示考虑任务分配尽可能均衡,即分配给某资源所有任务数量之和处于任务分配平均数±1范围内[7-8]。

2 算例仿真

为验证模型一与模型二的合理性和可行性,本文选取某机场某日从10:00到13:00之间的航班保障任务分配作为研究对象。模型一所需数据如表3所示,可计算出最少所需资源数量,模型二所需任务清单重复利用表3,在岗资源清单可根据当日在岗资源情况获取,由于航班保障任务与保障资源匹配权重矩阵决定了任务分配的方式,同时其权重矩阵的影响因素很多,本文定义了0～5作为权重值来加以说明,其中,0表示保障资源不具备保障该航班条件,其他数值越高表示越适合保障该航班。具体数据见表4。

表3 航班保障任务清单

表4 航班保障任务与保障资源匹配权重

在系统设计方面,从低耦合度以及业务无关性角度考虑,将航班保障资源调度算法服务独立部署,数据以参数方式进行传递来减少对实际生产系统的影响。通过MATLAB的混合整数规划模型根据业务需求进行封装并编译,形成独立服务部署在Linux服务器上,通过HTTP协议以POST请求方式进行调用,请求参数采用Json格式。实际生产环境为企业私有云平台,硬件配置为8核CPU、64 G内存、1 T硬盘,运行于Red Hat Enterprise 7.6,JDK1.8环境下,各项任务按照每天1000个航班做压力测试,其计算时间均小于5 s,完全满足实际工作要求。根据本文测试验证数据,模型一算法模拟器核心目标为当前所有任务分配所需要最少资源,计算结果的保障任务分配情况如图2所示。模型二计算结果如图3所示,其核心目标为当前任务、资源和分配权值条件下,同时考虑任务分配均衡的约束,所能分配结果的权值总和最大,即为最优化任务分配方式。

图2 模型一任务分配计算结果

图3 模型二任务分配计算结果

3 计算结果分析

由于模型一主要目标是为解决航班保障资源预排班问题,经机场全量数据验证,航班保障调度排班资源反馈其结果完全能够满足作为资源分配的参考依据,特别是当航班量变化较大,比如航班换季期间,很好地解决了人员冗余和资源短缺的问题。

某机场原有任务分配方式为先空闲先排班(FFFS)原则,主要考虑的约束条件为工作量均衡,以表3中的数据为例,实际任务分配情况如图4所示。依据模型二的约束条件,不仅解决了先空闲先排班的工作量均衡需求,还能够结合航班保障与资源匹配权重矩阵,计算出最优资源调度结果。根据测试数据按照先空闲先排班结果计算出的总计权重值合计为52,而根据混合整数规划模型二计算出的最大权重值合计为81,由此可见所提出的模型算法较先空闲先排班规则具有明显的优化和提升效果。