基于自适应大规模邻域搜索算法的多等级引航员排班问题

萧理阳，郑航晓，孙 鹏，陈露娴①

（1.上海大学，管理学院，上海 200444；2.天津大学，管理与经济学部，天津 300072）

0 引言

船舶进出港是船舶航行中事故高发的环节[1]，大多数海港为了降低事故发生的概率，会安排引航员为船舶进出港环节提供引航服务。随着船舶出入港的需求不断增加，船舶入港作业时间更加紧凑，港口船舶调度难度加大。复杂的港口船舶流通现状对引航员能力提出了更高要求，也使得制定引航员与船舶调度计划的过程变得更加困难。

大多数国家对引航员分等级进行考核，给合格者授予引航证。在我国，引航员根据其能力水平被划分为三个等级，只有通过考核的引航员才能被允许在特定水域进行引航服务。多等级引航员是排班过程中不可忽略的要素，依照交通运输部海事局的《船舶引航管理规定》[2]，调度员需根据船舶大小、吃水以及运送物品种类等方面的不同，将不同难易程度的引航任务指派给相应级别的引航员。现实情况下，培养一个经验丰富的引航员往往需要十年以上[3]，大多数港口选择从有经验的船长中选拔和培训引航员。鉴于引航员从业人数少、培养难度高的现状，该行业目前仍存在巨大的人才缺口。另一方面，传统调度方法主要以人工操作为主，随着港口实际情况复杂化，人工排班造成的引航资源浪费和调度不合理现象也日益明显。对于港口企业而言，合理的引航调度排班可以更高效地利用港口现有的引航员资源，大大降低港口的运营成本。因此，如何合理地制定引航员调度计划提高引航调度的服务效率，成为当前港口企业亟待解决的问题。

现有与引航服务相关的研究文献可以归纳为两个方面：第一种从社会学的角度研究影响引航员工作效率的原因，如其疲劳度[4-6]、个人能力[7]、心理素质[8]、安全知识[9-10]和风险感知[11]等社会因素对引航工作的影响；另一种则是专注于构建引航员排班规则的模型，并根据排班模型设计相应算法[12]。Wu等[13]构建了一个考虑引航员换乘和航道容量限制的引航员排班问题模型，并开发了一种分支定价（Branch and price，B&P）算法来求解该问题。Gregory等[14]考虑了引航员工作排班不确定性的负面影响，在其模型中引入引航员最大连续工作时长和每周最大工作时长概念。Xiao[15]和谭哲一[16]则分别考虑了引航员疲劳度和船舶间的安全距离，并设计了一种两阶段变邻域搜索（Variable Neighborhood Search，VNS）方法对其提出的模型求解。上述文献虽然总结了引航员的稀缺性与差异性，但现有建模过程中通常假设引航员同质化，较少考虑引航员等级这一现实因素，并且多数模型作出引航员与任务数相等的假设也与实际的引航员人才稀缺现状不符。同时，引航员排班问题已被Wu[13]证明为NP 难问题，对于该类问题，目前主流的精确式算法求解该问题难度较高且时间较长，现实应用价值较小。而相关启发式算法，虽然没法保证解的最优性，但是可以在有限时间内找到与已知最优解相接近的高质量解。

本文以多等级引航员排班问题作为研究对象，构建了一个包含引航员等级与引航员人数限制的混合整数规划模型，并根据该问题的特点针对性设计了自适应大邻域搜索算法（Adaptive Large Neighborhood Search，ALNS）进行求解。为了提高算法输出解的精度与速度，在该算法中设计了领航任务开始时间判断模块和航道容量约束判断模块。为了检验该算法的性能，本文通过与CPLEX 商用求解器以及文献中的两阶段VNS 算法在精度、效率等方面进行了充分比较。

本文的创新点主要有以下三点：（1）构建了考虑了引航员等级、时间窗、航道容量等因素的引航员排班问题整数规划模型；（2）根据问题特征设计了ALNS算法，有较快的运行速度和较高的求解精度；（3）提出了相应的管理学启示，可为引航站调度中心的引航员排班决策提供参考。

1 问题描述及模型

1.1 问题描述

本文所研究的问题仅考虑一个引航站调度中心，调度中心中有数量限制的高、中、低三类不同等级的引航员。调度中心会根据港口管理局提供的船舶进出信息，在考虑航道和引航员相关信息后生成一个引航员调度计划。如图1所示，当船到达港口时，调度中心需要安排引航员对其进行进港引航服务；同样，当船即将离开港口时，也需要安排引航员对其进行离岗引航服务。在该问题中，假设每艘船必须有引航员对其进行引航服务，而在实际情况中部分引航任务难度较高，只有经验丰富的引航员才能胜任，所以把船的引航任务假设为三个难度等级（见表1），只有能力与之匹配或更好的引航员才能被安排该类船的引航任务，如图2所示。

表1 任务难度及对引航员等级要求Tab.1 Task difficulty and requirements for pilot levels

图1 引航示意图Fig.1 Schematic of pilot scheduling

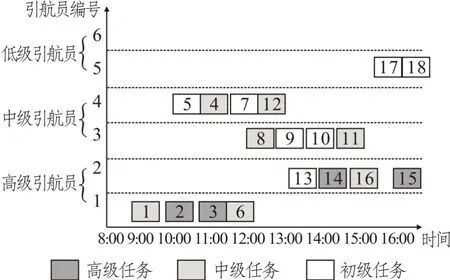
图2 引航员排班计划Fig.2 Pilot scheduling plan

同时，假设所有引航员初始都在位于靠近泊位的引航员调度中心待命，等到有任务安排之后乘坐交通工具到达目标点，换乘工具有直升机和快艇两种。引航员在完成单次引航任务后，可以原地休息等待下一任务或返回调度中心结束当天任务。为了防止出现引航员工作时间过长导致其因为疲劳而增大事故发生概率，规定引航员每天的工作时间不能超过工作时间上限Hˉ。

1.2 参数及变量

为了对模型进行更好的描述，模型中的参数和变量如下：

1.2.1 参数

Ν：所有任务集合，与任务集合相关参数下标均为i,j。

Νh：进港任务集合，Ν0为进港任务集合，Ν1为出港任务集合。

Νleνel：进港任务集合，leνel∈{0,1,2}。

Λ：任务类型，Λ={0,1}，0为进港任务，1为出港任务，下标为h。

L：任务等级集合，L={0,1,2}，0为高难度任务，1为中等难度任务，2为普通任务，下标为level。

qip：若引航员p满足服务任务i要求时为1，其他情况为0。

Ρ：可调度引航员集合，Ρ={1,2,…,|Ρ|}，每个引航员在一次排班中最多安排一个任务周期，下标为p。

Θ：引航员运输工具类型，Θ={0,1}，下标为k。

EF：规划范围内任务最晚结束时间。

T：在规划范围内的时间点集合，T={1,2,…,|EF|}，下标为t,t1,t2。

C：任务i的单位延迟成本。

C：一位leνel级别的引航员的班期成本。

C3：为一项任务提供引航服务的费用。

C：通过k型换乘工具换乘的单位成本。

C5：被服务船只的惩罚成本。

Ei：任务i的最早允许开始时间。

Di：服务于任务i所需的时间。

Οk：运输工具k的运输时间。

M：一个足够大的常数。

Βij：引航员在完成任务i后若立即执行任务j时需要换乘为1，其他情况为0。

1.2.2 变量

yit：如果任务i的开始服务时间为t时为1，其他情况为0。

ni：i任务未被安排服务时为1，其他情况为0。

1.3 数学模型

根据1.1 节问题描述，本文建立的模型以引航作业总成本最小为目标，构建模型如下：

1.3.1 决策变量

目标函数（1）为最小化引航作业总成本F，包括任务延迟成本（第一项）、引航调度成本（第二项）、引航成本（第三项）、引航员换乘工具成本（第四项）和未服务任务惩罚成本（第五项）。

1.3.2 约束条件

其中，约束（2）表示每个引航员班次最多分配一个开始时间。如果没有分配任何开始时间的引航员班次，则引航员班次为空。约束（3）表示每个引航员轮班最多有一个启动任务。约束（4）确保每个任务点都有安排。约束（5）为每个任务都被标记为安排或未被排班状态。约束（6）确保每个任务必须由符合其要求的引航员执行。约束（7）为每个任务分配一个开始时间。约束（8）表示引航员排班中第一项任务的开始时间不早于引航员轮班的开始时间，并且在引航员到达相应船舶的位置之前，第一项任务不能开始。约束（9）规定了在同一引航员轮班中连续执行的两项任务的开始时间之间的关系。约束（10）指定引航员轮班中最后一项任务的开始时间与引航员返回基地的时间之间的关系，并且确保每个引航员轮班的长度不超过每次工作时长上限。约束（11）为每个任务设置了一个时间窗口。约束（12）确保在引航员需要连续执行两个相同类型的任务时，使用换乘工具通过通道运输引航员。约束（13）对同时在航道航行的进港船只和离港船只的数量施加了上限。约束（14）～（18）定义了决策变量为0-1变量。

2 自适应大邻域搜索算法

上述模型所描述的多等级引航员排班问题属于NP 难问题，精确算法和CPLEX 等优化求解器难以在可接受的时间内求解该问题的中大规模实例。而ALNS 算法可以在较短时间内求解大规模实例，所以文章选择采用改进版的ALNS算法进行求解。

ALNS算法（见图3）为运用破坏算子和修复算子对解空间进行搜索的自适应大邻域搜索算法，最早由Ropke[17]在大规模邻域搜索算法（Large Neighborhood Search，LNS）的基础上提出，最初是用以求解带时间窗的取送货车辆路径问题。该算法在搜索过程中根据算子对解的改进情况自适应地选择搜索算子，对解的改进较好的算子在后续迭代中有更大的概率再次被选择来搜索解，以达到对解空间的高效搜索进而提高算法的性能。另外，为了跳出局部最优解，该算法还使用了模拟退火新解接受准则。在改进的算法中，设计了算子之间相互交互的功能（见图4）。同时考虑到引航员等级约束，算法中针对性设计了引航员降级破坏算子。

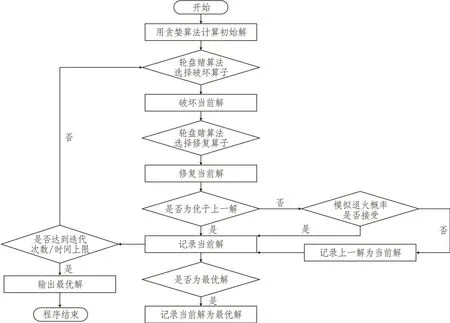
图3 ALNS算法流程图Fig.3 ALNS algorithm flowchart

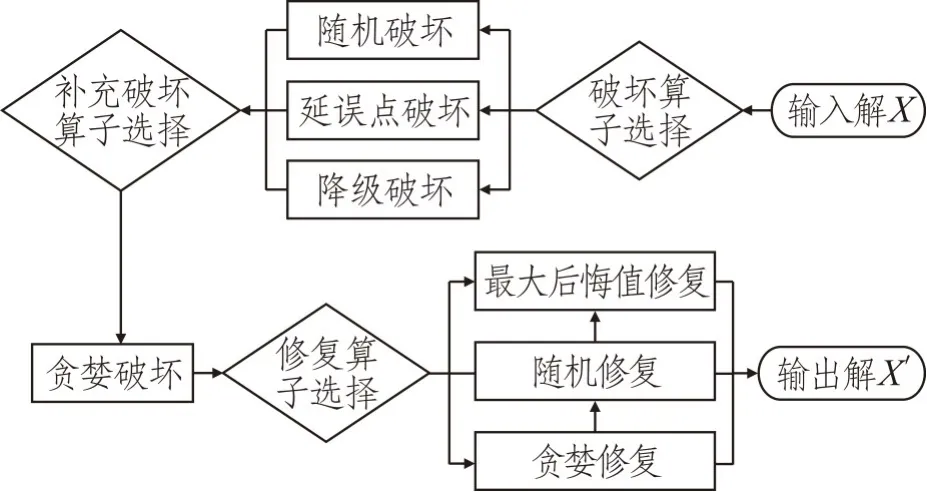
图4 算子选择与使用Fig.4 Operator selection and use

考虑到问题的复杂性，本文参考石敏涵[18]方案在设计算法的过程中将算法分为两层：外层通过构建ALNS 算法生成排班顺序方案（算法1），包括生成初始解、选择破坏算子与修复算子的轮盘赌算法以及模拟退火迭代算法。内层则是通过外层的排班方案，计算该排班顺序下的模型最佳被服务时间以及计算最小成本。

算法1：ALNS基本逻辑

2.1 内层程序

内层程序主要为引航总成本计算程序（算法2）。通过排班顺序只能确定引航调度成本、引航成本、未服务任务惩罚成本等较为固定的成本值，而计算任务的延误成本和引航员换乘工具成本则需要配合任务的具体开始时间数据。因此，内层程序考虑时间窗约束、引航员工作时长、换乘工具比较、航道容量约束等因素，生成具体开始时间starts_p。然后根据排班顺序结合任务开始时间计算任务总加权成本，辅助判断此次排班的质量。

算法2：内层算法

2.2 生成初始解

在ALNS 的算法中，初始解的质量十分重要[19]。本模块主要用贪婪算法[20]计算出模型的一个初始排班顺序。该环节通过内部算法辅助，逐一尝试把每个任务点插入到排班的所有可插入位置中并计算出每一次插入时当前的加权总成本，记住其中排班成本最小的一次作为该点的最优插入位置进行插入。当所有任务被确认插入成功后，记录当前加权总成本与排班顺序为当前解和当前最优解，供后续程序进行破坏和修复。

2.3 破坏算子

破坏算子通过删除路线上一定数量的节点，得到一条新的排班顺序。在这个过程中原有的路线会因为破坏算子删除的部分节点而发生变化。选择删除的逻辑主要有四种：随机破坏、贪婪破坏、延误点最长点破坏、降级破坏。被破坏的节点将被记录在pool 中，供修复算子进行修复操作时使用。前三种算子均为删除随机任务数，其中为了增加破坏算子的随机性使得能够探索更大的邻域，破坏算子之间允许组合使用，但是删除任务点的总数不能超过设定删除数量上限（R_max）。

2.3.1 随机破坏

随机破坏是从排班中随机破坏R_random 个引航员排班中的任务点，该算子运行速度快，但随机性强破坏效果较差。

2.3.2 贪婪破坏

贪婪破坏是执行R_random 次破坏任务，每一次破坏前尝试破坏所有可破坏任务点，并从中选出破坏时对总成本影响最大的一个任务点进行破坏，该算子运行速度最慢，但破坏效果最好。

2.3.3 延误点最长点破坏

延误点最长点破坏比较每个任务的实际开始时间与最早开始时间，记录其中差值最大的R_random个点进行破坏。

2.3.4 降级破坏

将中高等级引航员换为低一等级引航员，并对新引航排班中不符合条件的引航员进行删除。该算子可以帮助跳出只有部分高等级引航员参与的排班循环。

2.3.5 破坏算子组合使用

为了探索更多的领域，防止陷入局部最优解后循环相同或相似的破坏与修复程序，破坏算子需要有更高的随机性。算法设计在破坏算子的选择过程中贪婪破坏算子可以与随机破坏、延误点最长点破坏、降级破坏算子在一次破坏程序中共同被调用，通过多种算子之间的组合使用，可以很好地提高其他破坏算子的随机性。

2.4 修复算子

本模块通过重新插入被破坏算子删除的节点生成一个新的排班。Ropke 在大邻域搜索算法中提出了贪婪修复、随机修复和最大后悔值修复三种修复方式。在多数情况下贪婪修复和最大后悔值修复的效果好于随机修复，但是容易出现陷入局部最优解情况。所以为了提升算法的效率，修复的逻辑主要有四种：随机修复、贪婪修复、最大后悔值修复、修复算子组合使用。

2.4.1 随机修复

随机选择pool 中的部分任务点，选择排班内的某一符合插入条件的节点序列进行插入，并生成任务开始时间。随机修复算子随机性相当强，小规模地使用随机修复算子能够帮助算法很快地跳出原有的局部最优解。但也正是因为其随机性相当的强，导致其单独使用生成的解质量整体较差，并随着其修复点数增加解质量进一步恶化。

2.4.2 贪婪修复

贪婪修复即尝试对待插入的点在每一条排班的每一个序列点进行插入并重新计划开始时间，比较每一次插入对新排班带来的变化，选出其中变化最小的作为插入点。贪婪修复是多次比较生成解的修复方式，因为修复原理是以每个点的最优插入位置为目标，修复所产生的解的质量也是最高的。但因为固化的按顺序比较选取最优的算法流程，容易陷入局部最优解。同时，贪婪修复算法将那些对整体成本影响大的任务靠后插入，使得其插入过程中选择变得更小，这些任务点很可能有苛刻的要求需要被优先考虑。

2.4.3 最大后悔值修复

计算被移除任务点插回到已分配排班序列中的次优位置时其目标函数值与最优位置的目标函数值的差之和，然后选择差之和最大的需求节点及其最优位置。最大后悔值修复有着较好修复效率，相比于贪婪算子也能兼顾到对整体成本影响大的任务，但频繁使用也容易陷入局部最优解循环。

2.4.4 修复算子组合使用

单独使用随机修复算子效率较差，在修复算子的轮盘赌算法中若是选择了随机修复算子则有概率与贪婪修复和最大后悔值修复同时使用，考虑到随机修复算子随机性相当强，与贪婪修复和最大后悔值修复可以扩大其修复领域，从而帮助算法更好地跳出局部最优解循环，同时也保证了算法效率。

2.5 自适应机制

本章使用Pisinger 等[21]提出的轮盘赌轮选择程序来确定路由和节点选择方法。在一开始，每个破坏或修复算子的选择方法被分配相同的概率，然后，基于评分系统进行γ次主迭代后，动态更新每种方法的概率。由于不同算子得出的解质量有一定的差距，通过对解的优劣判断可以有效分析算子的使用效率，更多的使用高质量算子可以进一步提升算法效率[22]。因此本文针对性地设立了评分系统，规则如下：（1）如果在应用一种选择方法后获得了一个新的整体最佳解，则在该方法中添加ν1分；（2）如果当前的解较上一解得到改进，则增加ν2分；（3）如果该解决方案比当前的解决方案差，但根据接受标准被接受，则给该方法加ν3分。

评分系统被应用于算子选择的过程中，算子的评分越高就代表其效果越好，被选中的概率也就越高。假设s种算子权重为ωi(i=1,…,s)，得分为πi，选择算法的次数为ϕi次，ρ为0 到1 之间的系数，则可计算算子的被选择概率为：

2.6 迭代算法

本文使用了模拟退火算法的原理。首先设置一个最大迭代值Iter_max和最大迭代时间T_max。将生成的初始解导入后，利用轮盘赌算法选择出即将使用的破坏算子和操作算子初始排班进行振动操作。在这个过程中，如果新生成的解优于当前解，则对其新生成的解进行记录。如果该解优于已记录最优解，则将该解记录为最优解，否则按照模拟退火准则处理。当迭代次数或迭代时间达到最大值之后，停止迭代，输出当前的最优值和算子使用情况。

3 算例分析

为了检验问题模型和算法的有效性，并对影响排班成本的部分要素进行分析，文章做了以下两个部分的实验：

（1）对比大、中、小规模算例的改进版ALNS算法、CPLEX算法以及两阶段VNS算法结果。

（2）分析模型中关键参数对于系统运行总成本的影响，并总结算例结果进行分析，对多等级引航员排班问题提出管理启示。

3.1 算法有效性验证

在本节中，本文对多组数据进行计算实验，以验证本文所提出的改进版ALNS 模型和求解方法的适用性和有效性。本文数据基于对厦门港等多地的调研结果。文中假设以24 h 为一个调度周期单位，假定5 min 为一个基础时间单元。调度中心每天的最长工作时间为12 h及144个时间单元，而单个引航员每次最长工作时间为36时间单元。考虑到实际引航员人才较为紧缺，港口无法做到引航员数量充沛的理想情况，因此假设引航员调度中心常驻引航员数量为任务数量的一半。本文多等级引航员则参考厦门港引航站引航一科引航员比例，其中高等级引航员为9人，一、二级引航员为11 人，三级引航员和见习引航员为5 人，故本文将引航员高、中、低级比例确定为3∶5∶2，任务难度则参照上文表1 标准进行划分。进出港航道的初始容量均假设为同时可供两艘船并排航行。根据上述的数据进行不同引航员和船舶规模下的实验，本文总共测试12 组数据，用n_p_i命名不同的算例，n表示船舶的数量，p表示引航员的数量，i则表示该规模算例的索引，以此规则生成10、20、30、40和50 个任务算例，本文所用实验平台的CPU 为AMD 锐龙R5 5600H3.30 GHz，内存为16 GB，采用Windows11 64位处理系统，代码使用Java IDEA实现，所用CPLEX 求解器版本为12.6.1。实验结果如表2所示。

表2 两阶段VNS、改进版ALNS与CPLEX算法比较Tab.2 Comparison of two-stage VNS,improved ALNS and CPLEX algorithms

从目标结果的数值来看，10 个任务的小规模算例三种算法都得到了最优解，保证了在中小规模算例时解的质量。在求解方面，CPLEX 的求解所用时间明显多于两个启发式算法。而在任务船达到了20 艘以上的时候，CPLEX 均无法在三个小时内解出目标值，对于日进出船舶数量多、时效要求高的港口而言，CPLEX的实用性较差。

改进后的ALNS 算法和VNS 两阶段算法均可以在较短时间内获得一个可行解。相较两阶段VNS 算法，改进后的ALNS 算法平均总成本下降了52.68%。两阶段的VNS 算法虽然整体上求解时间更短，但是其在中、大规模的算例中难以保证解的质量，甚至在50 个以上任务规模的案例中多次出现了大规模任务点排班失败情况。

由此可见，改进版ALNS在规定时间可以保持较好的求解效率和精度，在解决的实际问题时，该算法总体上优于CPLEX算法和两阶段VNS算法。

3.2 关键参数敏感性分析

在实际情况中任务调度中心并无法修改任务船的实际需求，只能通过改变调度中心引航员的数量或扩宽航道等方式来对效率进行提升。同样对于决策者而言，增加或减少雇佣引航员的数量与航道是否需要扩容都是其在港口规划决策时所面临的选择难题。为了分析模型中港口实际过程中的关键参数对于最终结果的影响，本文尝试改变引航员数量、引航员各等级比例与航道容量等参数，并通过数据对比探究其对结果的影响。

3.2.1 引航员数量变化

原模型设定引航员总数为任务数量的50%（Ρ=|Ν|×0.5）。为探究引航员数量变化对结果的影响，下面通过假设引航员与任务数相等（Ρ=|Ν|）和引航员总数为任务数量的30%（Ρ=|Ν|×0.3）分别模拟引航员数量完全充足和引航员紧缺两种情况，并与原数据结果进行对比，结果见表3。通过对比可知在引航员数量充足的情况下，引航排班将会有更多选择，解的质量也能有小幅度的提升。但当引航员人数过少时，不仅时间延迟成本会受影响，还会涌现出大批的任务排不上班的情况，大大增加港口的运营成本。

表3 引航员数量变化结果对比Tab.3 Comparison results of pilot number change

3.2.2 引航员比例变化

下面将高、中、低级引航员的比例由3∶5∶2 改为2∶3∶5和4∶4∶2。

改变高、中、低级引航员比例的目标值对比结果见表4。高等级的引航员数量不足，往往会导致部分情况下任务的时间延迟增加，从而增大港口每天的运营成本。而在各等级领航员数量约为总任务数量一半的时候，在此基础上增加高级引航员比例，并不能对港口产生很多的正收益，在特殊情况下反而会使高等级引航员更多地参与到低难度的任务中，从而造成资源的浪费。从表中的整体情况上来看，高等级的引航员人数越多，每日排班的总成本就越低。

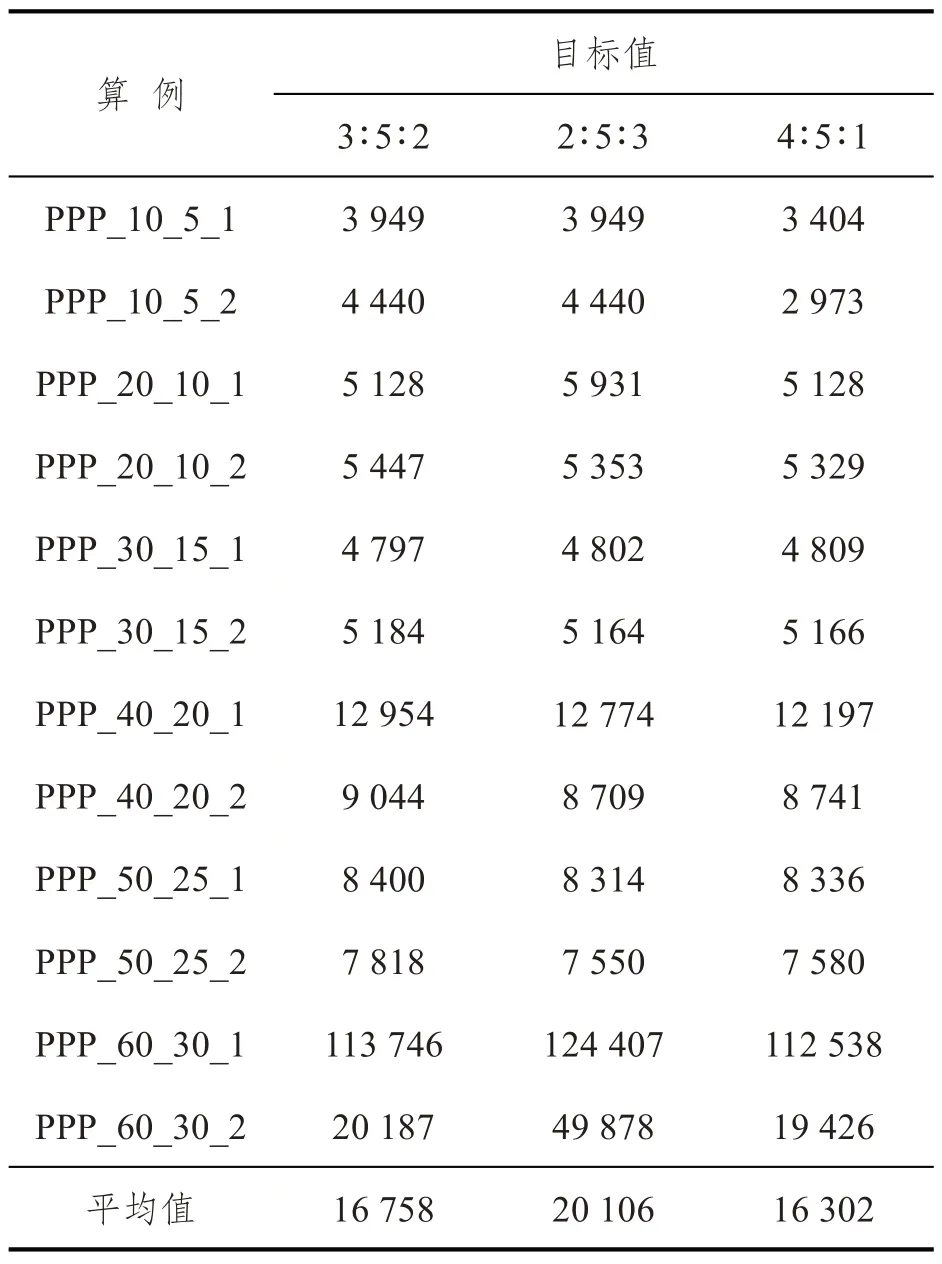
表4 引航员数量比例变化结果对比Tab.4 Results of pilot quantity proportion change

3.2.3 航道容量变化

进、出航道由2+2（进港航道允许最多同时航行2 艘船，出港航道允许最多同时航行2 艘船，下同）改为1+1 和3+3。改变航道容量后的目标值对比结果见表5。从表中的数据可以发现，总体上航道容量越大则其解越优。而在当天任务量比较多的情况下，航道少的港口往往会因为航道拥挤无法当天完成引航任务，为港口造成较大的延误损失。而在中小规模任务的情况下航道规模的影响并不是那么明显。如表5中，当每日任务数量达到40 个的时候，航道1+1 便出现了任务当天无法完成的情况。同样，当每日任务数量达到60个时，航道2+2条件也难以满足实际任务的需求。

表5 航道容量变化结果对比Tab.5 Comparison results of channel capacity change

综上，通过对算例结果的分析，可以得出以下结论及系统运营管理建议：

（1）若每日的任务量在一个合理的范围内，扩宽航道并不会对每日的成本造成较大的影响。相比于扩宽航道的成本，多数情况下港口扩宽航道带来的收益并不明显。而在排班任务密度过高或排班需求增速很快的情况下，适当的拓宽港口的进出航道容量，可以缓解港口每日服务船舶过多或者港口服务需求增长过快带来的压力。

（2）在一定范围内，能力高的引航员能够给港口带来更多的收益，鉴于社会上目前高水平引航员欠缺的实际情况，港口企业需要注重吸引和培养人才，保证其引航排班时可调度引航员比例在一个合理的范围内。而在引航员的数量达到一定规模后，增大中低等级引航员比例并不会对总成本造成大的影响，港口在吸收经验丰富的社会船员的同时也需要重视经验不足但是潜力巨大的年轻人才的培养和储备。

4 结论与展望

本文对港口的引航员排班问题进行了研究，考虑了时间窗、航道容量等因素，以时间延迟成本、引航员出工成本、引航员换乘成本、单次服务成本以及当日未服务船的惩罚成本的总加权成本最小为目标。通过优化模型构建与算法设计，给出了一个调度周期内引航员排班方案。本文在ALNS 算法中加入了不同算子之间相互配合的功能，在增大探索邻域范围的同时更高频繁利用了其中效果较好的算子，从而增大找到最优解的概率。与CPLEX 相比，文中所改进的ALNS方法，能大幅度降低运行时间，并且在中小规模的实践中可以证明其解的精度有一定的保证，使得该模型在现实中能有较好的应用价值。

在未来的研究中，本文会进一步探索该模型的实用性。例如考虑船舶进出港口时间的不确定性对引航员排班带来的影响或是考虑船舶靠岸作业情况构建一个完整的船舶进出港口周期模型。此外，考虑模型的复杂性特点，在未来的算法设计中可以融入变邻域搜索算法等其他算法的思想，提高解的精度。