考虑航段复杂度的机场终端区进场程序设计与评估

汤荣亮，王子明，王艳军*①

（1.南京航空航天大学，民航学院，南京 211106；2.中国民用航空华东地区空中交通管理局江苏分局，南京 210000）

0 引言

交通运输业是我国的重要战略产业，高质量的交通运输系统能够在预期的时间内将人或货物运送到目的地，对促进国民经济发展等具有十分重要的意义。随着经济的发展，无论是公路交通运输、铁路交通运输还是空中交通运输市场的运输量持续增加，在各个交通运输系统中的拥挤和延误现象日益严重。交通拥挤会带来巨大的经济损失并造成严重的环境污染。为了解决交通拥挤问题，一种方法是通过合理分配交通流等方式最大化利用现有交通系统资源，提高交通运输效率[1-4]。另外一种方式是通过增加交通系统容量来适应更多的交通运输需求，例如增加高速车道数量、新建机场跑道和航站楼等。随着航班的持续增加和空中交通系统容量的限制，机场和空域变得越来越拥挤，航班延误现象日益严重。终端区空域拥挤已经成为航空运输系统的瓶颈之一。终端区内航班拥挤不仅会导致航班延误、取消等问题，给旅客带来不便，更重要的是会对运行安全造成严重影响。因此，研究如何解决机场终端区交通需求持续增长导致的空域拥挤和运行压力等问题，对于改善航空运输的运行效率、提高旅客出行体验都具有重要意义。

空管系统中的点融合系统是一种先进的技术手段，可以将多个飞行区的航班点进行融合，形成单一的控制区域。点融合系统是指支持点融合技术运行的基于性能导航（Performance Based Navigation，PBN）空域结构。该系统由一个融合点和与该点等距（垂直分离）的两条或多条排序边组成。将飞行管理系统、水平导航功能与雷达引导方法相结合，实现优化多向进场交通流排序与间隔管理[5]。点融合系统是民航领域的一项重要技术，这种技术可以提高机场终端区的运行效率和运行效益，提高机场终端区的安全水平。虽然点融合系统的设计有一定的原则，但是当前关于根据进近空域运行特征设计点融合系统并评估的研究工作较少，如何结合机场终端区特征，设计点融合系统对提高机场终端区的运行效率和安全水平、推进民航强国建设和高质量发展、提高我国民航产业的整体竞争力和国际地位等有重要意义。

国内外对于机场终端区的研究主要集中在航班进离场排序、空域复杂度测算等方面。例如，Pierre 等人[6]提出了一种算法，用于终端机动区的有效轨迹规划；Gianazza 等人[7]比较了几种机器学习方法，从历史数据中学习空中交通管制员工作量的模型；Delahaye 等人[8]提出了一个基于动态系统的新的空中交通复杂性指标，基于一组雷达观测值（飞行器位置和速度）构建了一个对这些数据进行插值的矢量场；Dahlberg 等人[9]提出了一个混合积分编程框架，用于设计终端操纵区中的飞机进港路线，以保证飞机在时间上的分离，输出的路线构成了操作上可行的合并树，并保证终端操作区中的整体交通模式可以被空中交通管制员监控；Chevalier 等人[10]在考虑了跑道的配置、机场的周围环境和操作限制等因素的基础上，提出了一个设计离港和进港航线的有效设计方案；Raúl Sáez García 等人[11]提出了一种混合整数程序设计方法来计算飞机在终端机动区的进港路线，以保证所有在给定时间段内进港的飞机在时间上的分离，并且飞机按照最佳的连续下降运行速度曲线和空载推力飞行；王超等人[12]通过对终端区雷达航迹进行分析，研究了空中交通管制行为的特点，讨论不同控制策略下的机头时距演化特性和不同相态下的机头时距演化特性；游录宝等人[13]研究了点融合系统的概念、设计、运行与优化，并结合实际案例对研究内容与方法进行验证；谢丹红等人[14]进行了终端区点融合系统的研究与论述；赵嶷飞等人[15]从交通运输角度，审视空中交通管理实践发展历程、学科知识和研究方法积累过程；张军峰等人[16]针对PMS 的运行模式和多个利益相关方的需求，构建PMS多目标排序与调度模型，提出基于多目标的帝国竞争算法，经验证得知该算法有良好的实际应用效果。

虽然有关进港离港的排序以及运行优化的研究已经取得非常丰硕的成果，但是将研究中所提出的机场终端区运行优化方法在实际机场中进行应用的案例不多。如何结合机场附近空域结构，识别空域运行瓶颈，设计适用于机场空域的点融合系统是需要解决的问题。因此，本文深入分析点融合系统在南京禄口国际机场的应用，构建出点融合系统的运行效率评估系统并对点融合系统的整体运行效率进行科学评估。本文主要贡献如下：考虑机场附近航段的结构和流量特点，构建航段复杂度计算模型，识别空域运行瓶颈；基于所识别的空域运行瓶颈，为南京禄口国际机场设计了点融合系统，并使用AirTOP 仿真软件验证了点融合系统的效率。结果表明，点融合程序可以缓解平均进场延误，同时降低管制员平均负荷。

1 基于航段复杂度的空域运行瓶颈识别

航段的繁忙程度可以描述为动态交通流在静态航段结构限制下产生的非线性等复杂的联系。复杂度表征了局部与整体之间的非线性形式，因此复杂度的研究可以较好地解决航段繁忙程度的划分需求。目前，由于复杂度缺乏统一的定义，针对航段复杂度的分析及其繁忙等级划分仍然没有统一标准。一些学者将内禀复杂性定义为航空器与空域结构相互关联，反应了航空器的无序性对复杂性的影响[17]，或分析扇区复杂性与管制员工作负荷之间的关联并以此作为扇区划分的依据[18]。研究发现，部分空域结构指标和交通流影响指标对交通复杂度产生影响[19]。基于此研究，本文以航段为视角，按照空域静态结构特征和飞行流量动态特性，基于航段的结构和流量特点，构建航段复杂度计算模型，识别空域运行瓶颈，为点融合系统设计提供基础。

1.1 基于基尼系数的流量分布评价

基尼系数（洛伦兹系数）通常用于综合评价居民内部收入分配差距水平，现被广泛应用到污染物排放分配、资源配置、水资源利用等领域。基尼系数计算如图1所示，具体公式如下：

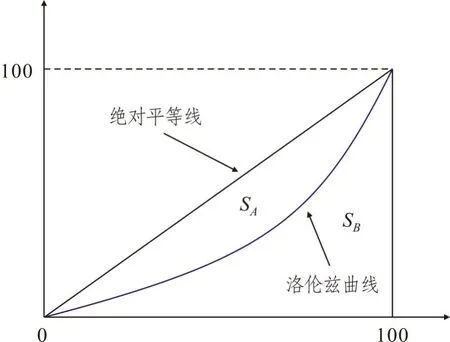
图1 洛伦兹曲线示意图[20]Fig.1 Schematic of the Lorentz curve

当SA=0 时，基尼系数GI=0，表明不存在分配差距，SA的值越大，则表明分配差距越大，分配的越不公平，空域内流量在时间和空间的分布越不均匀。因此，基尼系数可用于评价空域内流量在时间和空间分布的均匀性。

1.2 航段复杂度定义

航段是空中交通运输网络中的重要组成部分，如图2 所示。航段根据其自身的物理结构，承载并容纳了空中交通流量在扇区中的飞行流量。在保证运行安全的基础上，航段的复杂程度用由航段构成的交通航路航径的数量和流经该航段的交通流量进行描述，其所构成的航路航径数量越多，交通流量越大，则航段的复杂度越高。因此，航段复杂度需要从航段静态结构和航班流量分布两个维度构建。

图2 航段结构示意图Fig.2 Schematic of the route leg structure

（1）航段静态结构：基于已有空域结构可知，航段作为航路网的组成部分，与其连接的多条航路共同组成航路运输网，其静态结构维度可以用首尾两个航路点连通度表征。其中，航路点连通度di表示航路点i所连接航段数量，体现了航路点的联通度。联通度越高表明该航段在规划层面的重要性越高，即拥有更高的预计通行量，必然带来较高的繁忙度。航路a的连通度可表示为：

（2）航班流量分布：航班流量的大小和分布均匀程度均对空域的复杂程度起到决定性作用，因此航班流量分布维度包括流经航段流量和航班流量分布不均匀系数。其中航班流量分布不均匀系数采用基尼系数计算。

航班流量分布不均匀包括时间和空间上的分布不均匀：

式中：fa,x表示航段a在高度层x上的总流量，1 ≤x≤n；GItime(fa,x)表示在高度层x中，航段a的流量时间分布的基尼系数，体现了不同飞行时间段内流量分布的不均匀程度，间隔为5 min；fa表示航段a的总流量；GIleνel(fa)为统计时段内航段a所有高度层流量空间分布的基尼系数，反映了航段不同高度层的流量分布不均匀程度。因为当航班绝对均匀分布时，基尼系数为0，这与实际运行不符，故采用基尼系数加1进行修正。

1.3 航段复杂度指标

鉴于航段与其相邻的航段间会产生相互影响，因此需要计算航段之间相互影响系数ra,b，且基于航路运行的特点，当两航段其中一条为流入航路节点，另一条为流出同一航路节点时，视为两条航路连通，ra,b值为1。否则，参照碰撞风险与航段夹角知相互影响系数计算公式如下：

式中：θ为航段之间的夹角。

航段a与相邻航段之间的影响程度ra可以表示为：

鉴于不同航空器类型和航段流量密度对于空中交通的运行影响程度较大，因此将机型混杂系数mixi和航段距离纳入航段复杂度模型。航段a的复杂度表示为：式中：fa表示在指定时间段内通过航段a的流量；为目标空域内所有航段的流量总值；Da表示航段a的距离；D为目标空域内所有航段的距离总值；ΝH、ΝM、ΝL分别为重型机、中型机、轻型机数量。

由上式可知，当fa为0 时也为0，表示无航班流量时，航段复杂度为0，这与实际运行相符；当fa、da、ra均增大时也增大，与前文描述的航段复杂度定义相符，因此综合考虑了航段的静态结构、交通流量等因素，能客观反映航段之间的相对复杂程度。

1.4 航段复杂度与扇区复杂度和飞行程序的关系

为便于管理空中交通，有关当局（例如空中交通管理部门）将空域划分为不同规则的几何体，称为扇区（Sector）。每个扇区通常包含多个航段，并且由一至两名空中交通管制员负责指挥其中的交通。扇区复杂度受到空域结构（航段组成）、交通流分布等因素的影响，直接影响管制员的工作负荷和扇区容量。本文并未采用扇区复杂度分析空域运行瓶颈的主要原因在于本文的目的在于识别进近空域中的运行瓶颈，进而设计相应的点融合系统。扇区复杂度是考虑扇区内所有航段以及管制员指挥下得到的空域运行情况评价。

飞行程序是预先定义的飞行路径，指导飞机从终端区空域进入点飞行至特定机场跑道，或从跑道起飞后直至离开终端区的运行路径，旨在确保飞机有序安全地进入和离开终端空域。划设进离场飞行程序的主要目的是使得航班遵循固定的飞行路径，实现有序的交通。航段复杂性是基于飞行程序结构和交通流分布得出的反映实际运行过程的复杂性。合理的飞行程序设计有助于高效管理交通、增强安全性，并减轻空中交通管制员的工作负担，所有这些都有助于综合管理复杂的终端空域。

2 点融合系统设计原则及方案

2.1 点融合系统简介

传统的终端区空域程序设计采用将交通流汇聚到跑道的延长线，而点融合系统设计采用单点合并到达航班流。从合并点开始，飞机通过固定路径加入最后进近。在合并之前，程序的一部分（排序弧）在必要时专门用于路径拉伸/延迟吸收。这些弧被设计成与汇合点等距的“准弧”，一旦获得与前一架飞机所需的间距，就可以通过沿航段向每架飞机发出的单一直接指令来实现排序。当获得交通许可时，飞机可以在不使用航段的情况下获准进入合并点。由于飞机之间间隔的可预测变化，管制员在确定进场顺序和发布“直飞”指令的时机选择将变得非常简单。管制员显示屏上的简单距离标记（以合并点为中心的距离环）足以支持这种运行（如图3所示）。一旦飞向合并点，机载系统就会计算出需要飞行的距离，飞机可以从航段高度层/高度连续下降，只需要调整速度以在航向合并点时保持间距。

图3 具有两个平行、垂直分离且方向相反的点融合系统设计示例[21]Fig.3 Example of a point merge system design with two parallel、vertically separated and oppositel direction points

2.2 点融合系统设计原则

标准/通用PBN 设计要求适用于任何点融合设计，例如最小程序段长度、转角/最大航迹角变化。点融合设计过程应尽早让所有相关利益相关者参与，以下为点融合系统的特定原则：

（1）航路点类型：在点融合设计中，航路点通常应使用转弯预期（飞越）来定义。

（2）航路点命名：战术航路点尤其是汇合点，应使用五个字母的可发音名称。

（3）其他交通流：与其他交通流（起飞流，在复杂空域的情况下从其他附近机场到达/起飞）进行程序隔离将影响各种程序段的3D定位和尺寸。

（4）排序航段：在可能的情况下，建议使其主要对称轴与主要风向/跑道方向对齐（即排序航段垂直于该方向）设计点融合系统，尽量减少不利情形的发生。

（5）水平尺寸：排序航段的长度以及排序航段与融合点之间的距离，应以容量、燃油效率/环境影响之间的权衡为指导。

（6）垂直尺寸：虽然排序航段的高度取决于到最后进近点的距离和满足连续下降的需要，但还可能需要考虑其他当地因素，例如可能对过渡高度的干扰。

（7）融合点和加入最后进近：在靠近跑道的进近扇区，尤其是融合点之后，程序设计可能会受到环境限制的影响。

3 实例分析

3.1 南京进近空域简介

南京进近空域由中国民用航空华东地区空中交通管理局江苏分局（以下简称江苏空管分局）提供空中交通管制服务。2020年，南京本场及周边南通、无锡、常州、扬州、合肥等航班量迅速增长，南京02、03和04扇区压力进一步增大，拟调整02、03和04扇区的范围，并在其基础上增设06扇区。06扇区主要负责南京机场半塔（OF）方向航班进离港，以及合肥、盐城、淮安、徐州、连云港、无锡、南通、常州、扬州等机场的进离港航班。整个空域调整后如图4所示。

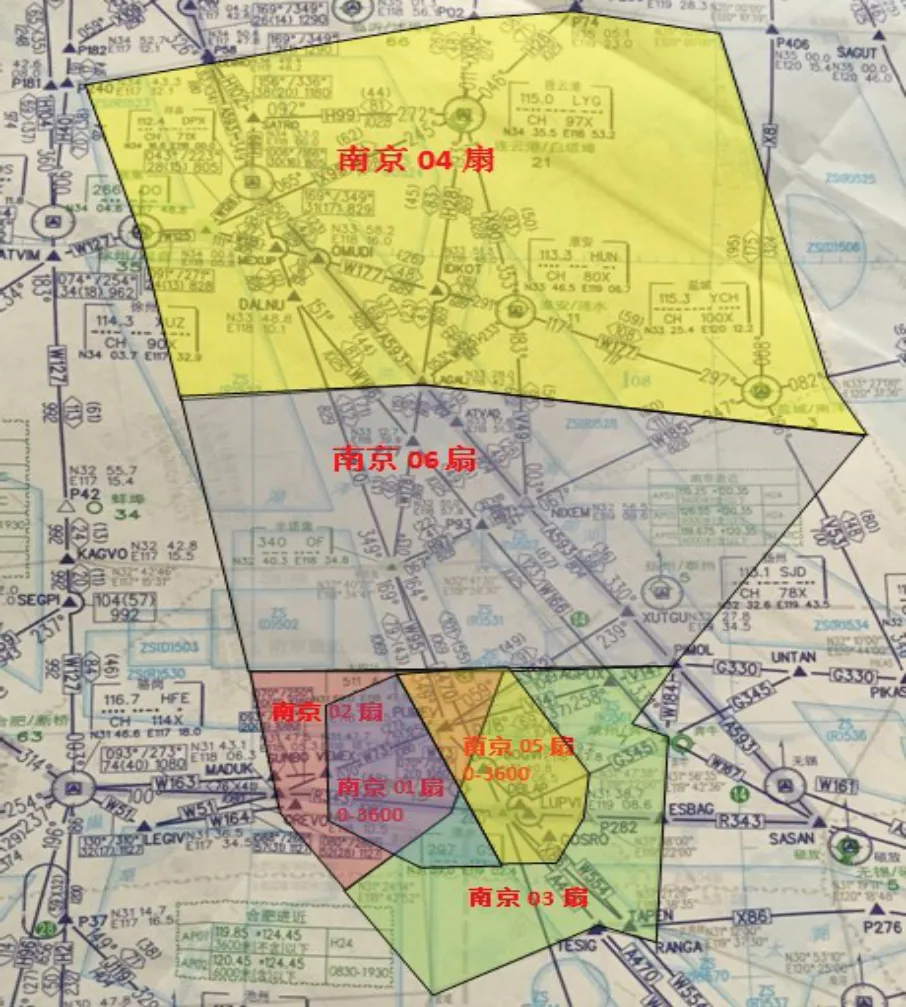
图4 2020年南京进近管制扇区Fig.4 Nanjing approach control sector in 2020

3.2 南京进近空域运行瓶颈识别

以禄口机场进场航段和部分进近航段为例，参考实际的管制经验选取11 个需要重点关注的航段进行航段复杂度的数据统计分析，对统计时间段内每个统计日同一统计时段的复杂度进行均值处理，用于描述各航段的整体复杂度。以2019 年5 月18 日为例，部分统计结果如图5 和图6 所示，图中“6”表示统计时间范围为06:00～06:59，其余类推。

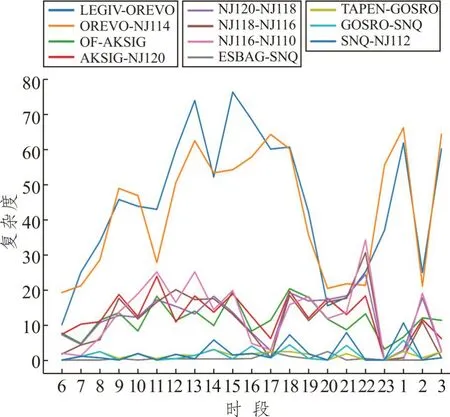
图5 部分航段复杂度对比图Fig.5 Comparison plot of the complexities of selected route legs

图6 部分航段复杂度箱型图Fig.6 Box plots of selected route legs complexities

如图5 和图6 所示，不同方向航段的复杂度值存在较大差异。其中，HFE方向的LEGIV-OREVO和OREVO-NJ114 航段的复杂度远大于其他航段；OF 方向的5 个航段OF-AKSIG、AKSIG-NJ120、NJ120-NJ118、NJ118-NJ116、NJ116-NJ110 为第二梯队，由于该方向航班到达集中度明显低于HFE方向，航班流较为平稳且顺畅，故而5 个航段复杂度较为相近且相关度较高。表1 给出了9 个重点航段统计时间范围内共651 个统计时间段的复杂度进行0 占比、最大值、平均值、非0 平均值、标准差、非0 标准差的统计，真实反映了各航段在南京进近的作用和角色。

表1 航段复杂度统计结果Tab.1 Results for route legs’complexity statistics

（1）无论从均值还是最大值来看，HFE 方向的LEGIV-OREVO 和OREVO-NJ114 航段均保有最大的复杂度，且未出现无航班经过的情况。LEGIV-OREVO 为禄口机场HFE 方向进场的主要起始航段，虽然距离较长（57 km），在仅有4个主要可用高度层的情况下，承载了南京进近60%的进场航班，航班流量极为集中，复杂度最高。OREVONJ114 为LEGIV-OREVO 的后续航段，得益于可用高度层数量上50%的提升，航段复杂度总体上低于前序航段。而且，因为更加临近跑道，航班的高度层配置等已近趋向平稳，故而保有较低的标准差。

（2）OF 方向五条航段的复杂度整体上低于HFE 方向，前四个进场航段在复杂度分布特征上较为接近，作为进近三边航段的NJ116-NJ110航段的复杂度取得峰值。NJ116-NJ110 为禄口机场OF方向进场程序三边，该航段上的航班与HFE 方向进场航班呈相对的运行趋势，且可用高度层较少，空间狭小，飞行冲突较为突出，致使其复杂度高于其他四个航段。值得注意的是，NJ116-NJ110 航段出现0繁忙程度的比例显著高于其他航段，原因是在OF 方向进场航班排序靠前时往往采取直飞策略并不使用该三边进场程序造成的。

（3）EABAG 以及TAPEN 方向的航班相对较为分散，航段空闲时间较多，呈现为稳定的低复杂度状态。

综上所述，南京进近空域内HFE 和OF 方向航段航班集中，复杂度高，容易造成拥堵。这与管制员主观认知相符，与实际运行相匹配。因此，在HFE 和OF 进场方向应用点融合系统，简化雷达管制过程，减少管制指令，降低管制员和飞行员工作负荷，改善陆空通话频道的拥挤，将有效提升空域运行安全。

3.3 南京进近PMS程序设计方案

基于点融合系统的设计原则和南京进近空域运行实际，提出以下点融合系统设计方案，如图7所示。

图7 南京进近点融合系统设计方案Fig.7 Nanjing approach point merge system design program

（1）融合点选取。通过上文中关于进近空域内拥堵点的识别，选取融合点位于HFE 和OF 方向进场轨迹的交汇点，交通流开始汇聚整合的定位点作为程序融合点。基于空域环境，将其高度设定为1 800 m（6 000 ft）。

（2）排序弧设定。融合点位置有HFE 和OF 方向两条进场航线，因此为其分配两条排序弧。每条排序弧分别占用一个高度层，相邻高度层之间垂直间隔为300 m，内高外低。基于南京禄口机场终端区的空域环境、航线结构和流量分布，外排序弧的高度选择2 400 m（9 000 ft），内排序弧的高度选择2 700 m（10 000 ft），两条排序弧之间水平间隔调整为9 km。

（3）程序参数。由于南京禄口机场飞行程序是以PBN 飞行程序为主用程序，导航规范为RNAV1，本文点融合系统方案设计的飞行程序导航规范为RNAV1。点融合系统的角度参数如下：进入变化角α为45°，直飞变化角β为90°，退出变化角γ为0～40°，包围角δ为70°。内排序边高度为2 700 m、融合点高度1 800 m、内外边距离40 km、边-融合点距离45 km、内排序边长度10 km。南京进近管制员一般在会在IAF点之前，将航空器的速度调整至180 节。对于PMS 程序，由于排序边距离IAF点的距离至少在30 km，设定PMS方案的内排序边的速度为200节，融合点的速度为180节。

3.4 仿真结果分析

为了验证本文所设计的PMS系统的效率和效益，采用计算机快速仿真对比传统进近程序和PMS 程序的效果。计算机快速仿真采用AirTOP仿真软件构建计算机仿真模型，输入航班计划进行快速仿真，对比两种程序下的航班延误和机场容量。

3.4.1 仿真实验设置

（1）实验场景。在AirTOP 仿真实验中，南京机场东向运行，使用跑道为06/07，采用的跑道运行模式为独立进近。

（2）航班计划。本次仿真实验面向未来航班量，即24小时内共403架次进场航班。

（3）飞行程序建模。根据设计的进场程序进行建模。

（4）仿真参数设置。计算机仿真中，进场移交间隔为20 km，连续两架进场间隔为4 nm。

3.4.2 结果分析

图8 展示了点融合程序下进场每小时平均延误和实际降落情况，图9～图15 展示了不同运行方式原始程序下进场每小时平均延误和实际降落情况。表2 展示了PMS 程序和不同运行方式下的情况对比，包括一天内平均进场航班延误和总的进场航班数量。通过图8 可以看出点融合程序下进场延误高峰出现在12:00～13:00，其他时间延误水平较低，平均进场延误小于2 min/架次（不包括0:00，12:00～13:00）。通过图9～图15 和表2 可以看出随着进场航班数量的增加，平均进场延误呈现上升趋势，越来越多的时段拥有较高的平均延误。从运行方式00～06，进场航班数量从323 增加到508 架次，平均延误从01 分12 秒增加到07 分51 秒每架。在点融和程序下，进场航班数量534，而平均进场延误仅有3 分34 秒每架次，作为对比运行方式04 进场航班数量为439，平均进场延误为3 分50 秒每架次。点融和程序优化了进场交通流，保证了运行效率，减少了平均进场延误。

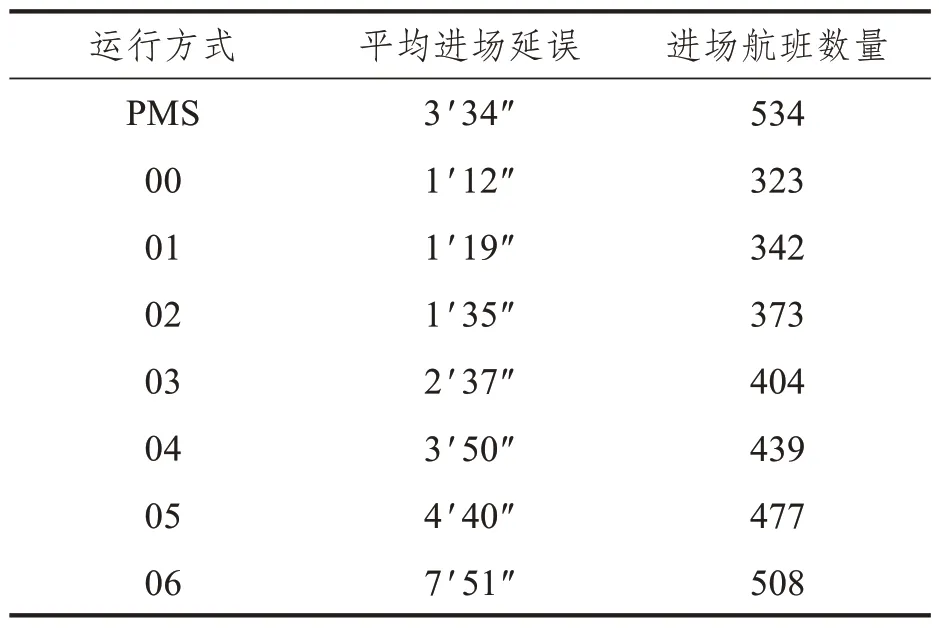
表2 PMS程序和不同运行方式下的情况对比Tab.2 Comparison of the situation under the PMS and different operating mode programs

图8 PMS仿真进场平均延误和实际降落图Fig.8 Average approach delay and actual landing under PMS simulation

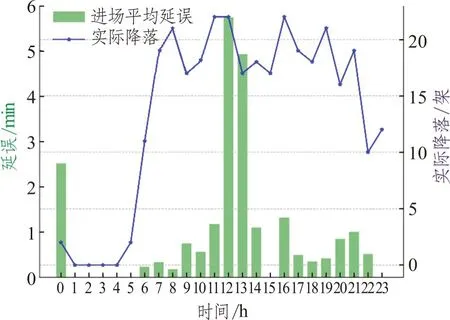
图9 运行方式00下平均延误和实际降落图Fig.9 Average approach delay and actual landing under operation mode 00

图10 运行方式01下平均延误和实际降落图Fig.10 Average approach delay and actual landing under operation mode 01

图11 运行方式02下平均延误和实际降落图Fig.11 Average approach delay and actual landing under operation mode 02

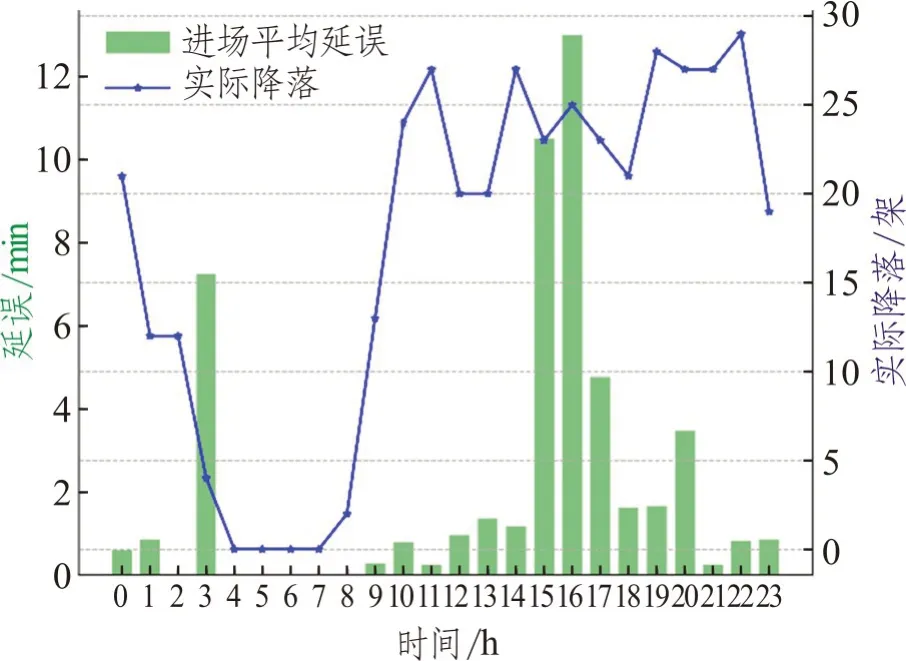
图12 运行方式03下平均延误和实际降落图Fig.12 Average approach delay and actual landing under operation mode 03

图13 运行方式04下平均延误和实际降落图Fig.13 Average approach delay and actual landing under operation mode 04

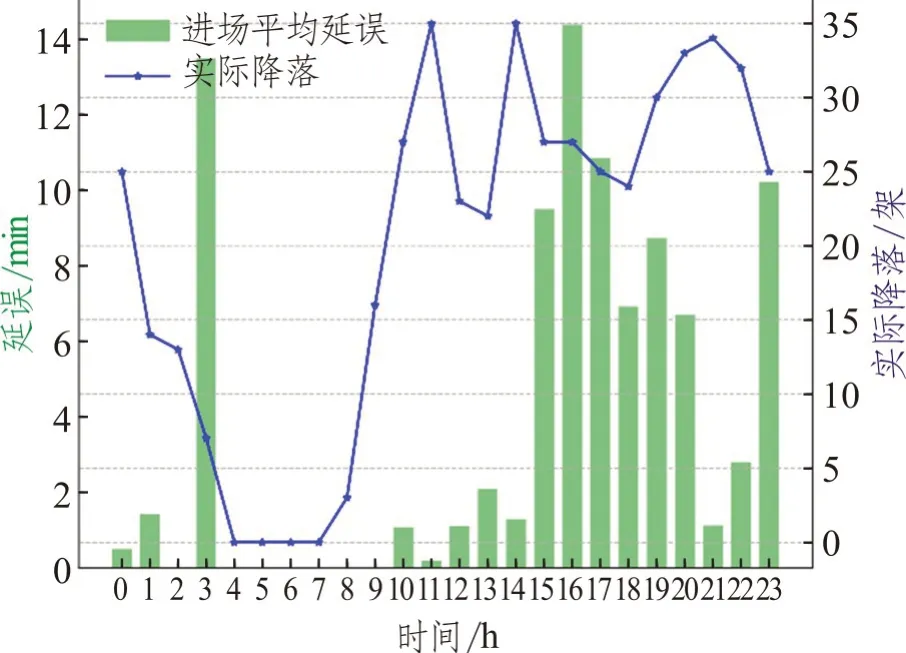
图14 运行方式05下平均延误和实际降落图Fig.14 Average approach delay and actual landing under operation mode 05

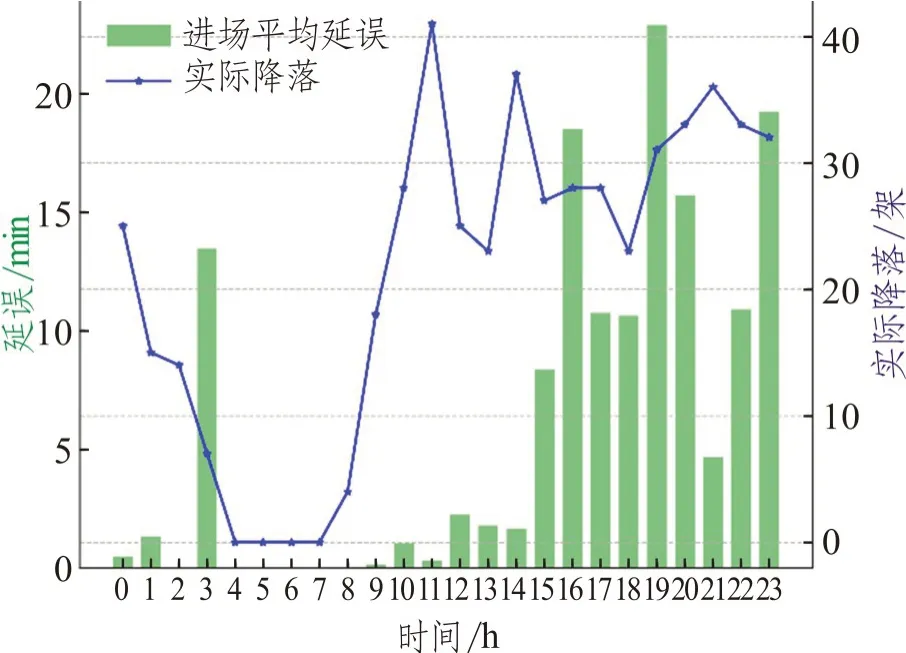
图15 运行方式06下平均延误和实际降落图Fig.15 Average approach delay and actual landing under operation mode 06

表3 展示了原始程序和点融合程序的情况对比。通过使用点融合程序，平均进场飞行时间由20 分50 秒降低到19 分48 秒，平均进场延误从3分11 秒降低到1 分13 秒，平均管制员负荷从85.93%降低到76.68%。点融和程序有效降低了管制工作负荷，提高了空域运行效率，降低了进场延误。

表3 两种程序下的情况对比Tab.3 Comparison of the situation under the PMS and original programs

3.4.3 航段复杂度对比

为了验证本文所设计的PMS 系统相较于原始程序的航段复杂性变化，计算了PMS 程序下的航段复杂性。如图16 所示，对比原始程序和PMS 程序下不同进场方向中航段最大平均复杂度，PMS 程序下航段复杂度在东边流量、北边流量和西边流量相较于原始程序都有所降低，而在南边流量有所增加。总的来说，南京进近空域中，HFE 方向航段的复杂度远大于其他方向航段复杂度，使用PMS 程序使得HFE 方向航段的复杂度降低。

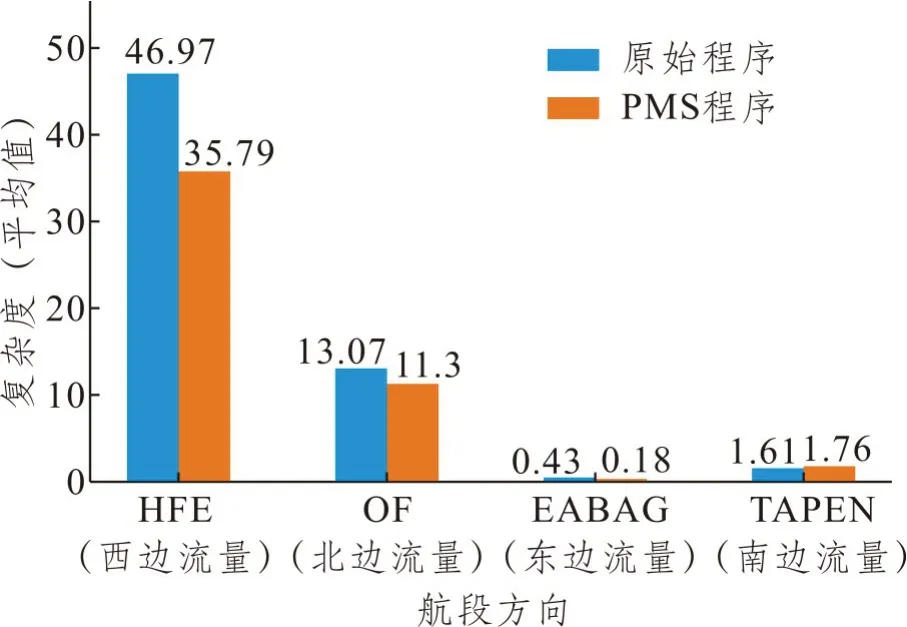
图16 原始程序和PMS程序下不同进场方向中航段最大平均复杂度对比图Fig.16 Comparison of the maximum average complexities of route legs in different approach directions under the original and PMS programs

4 结论

本文以南京禄口国际机场交通基于航段复杂度的空域运行瓶颈识分析结果为基础进行了适用于该机场终端区的点融合系统的设计，并通过仿真实验验证了所设计的点融合系统相较于传统运行程序的优越性，为南京禄口国际机场终端区点融合系统的现实应用提供了强有力的理论研究基础，为空管系统的高效安全运行提供了科学的指导。主要创新和贡献如下：

（1）提出了航段复杂性计算模型用以识别终端区空域运行评价。本文以航段为视角，按照空域静态结构特征和飞行流量动态特性，基于航段的结构和流量特点，构建航段复杂度计算模型，识别空域运行瓶颈。以禄口机场进场航段为测试案例，建立了适用于南京禄口国际机场终端区的航段复杂度指标，并依据该指标进行了该机场终端区的运行瓶颈识别，结果发现南京进近空域内HFE和OF方向航段复杂度高，容易出现拥堵。

（2）基于空域运行评价设计了点融合运行程序，并在南京禄口国际机场进行了验证。本文基于航段复杂度计算模型设别了空域运行瓶颈，以禄口机场进场为例设计了点融合系统，并使用AirTOP 软件验证了点融合系统和传统运行程序。结果表明，点融合程序可以缓解平均进场延误，同时降低管制员平均负荷。

本文研究了基于航段复杂度的空域运行瓶颈识别分析下点融合系统，未来可以研究多点融合系统，将两个（含）以上的单个点融合系统并行运行，最终汇聚到同一个航路共用点，从而有效处理多个方向进场交通流的情形。同时在未来研究中应考虑为点融合系统设计复飞和等待程序，有助于航空器再次加入点融合系统，应对进场流量超出点融合系统容量限制的情形。