融合多源数据与元胞传输模型的高速公路交通状态估计方法
2023-12-12黄丹阳
易 术,黄丹阳
(四川智能交通系统管理有限责任公司,成都 610200)
0 引言
高速公路交通状态估计是交通领域中的一个重要研究方向。随着交通需求的不断增加和道路容量的有限性,高速公路交通拥堵问题日益突出。准确估计高速公路交通状态对于交通管控和决策具有重要意义。交通状态估计是指基于交通先验知识利用实时数据,对路段上的交通状态变量,即流量、密度、速度等进行推断的过程。先验知识(即假设)可以来自数据驱动模型或物理交通流模型,通过运用统计/机器学习方法或利用物理原理抽象实际交通获得。根据所依赖的先验知识类型,交通状态估计方法可分为两类,即基于数据驱动的状态估计方法和基于模型驱动的状态估计方法。
基于数据驱动的状态估计方法(数据驱动方法)往往直接依赖于历史数据,而不是物理交通流模型。这类方法主要采用统计或机器学习方法从历史数据中提取数据之间的相关性,然后根据实时数据和相关性估计交通状态。早期的一些研究使用统计方法探索流量和其他变量(比如:速度[1]、速度方差[2]等)之间的统计关系,然后基于统计关系和实时数据进行交通状态估计。由于统计方法挖掘交通数据之间相关性的能力有限,学者们进一步提出了基于机器学习的估计方法。该类方法能够较好地处理非线性关系,如交通状态与时间、道路拓扑结构等因素之间的关系,因此主要应用于复杂交通网络场景[3–6]。Yu等人[7]提出了一种基于自注意力机制的长短期记忆网络模型(Self-Attention Long Short Term Memory,SA-LSTM)用于城市交通状态预测,并使用深圳市路网数据和浮车数据进行了实例研究,他们选取长短期记忆网络模型(LSTM)作为基线模型,与SA-LSTM 进行了对比,验证了SA-LSTM 模型预测的准确性。Liu 等人[8]结合交通流理论与深度学习,提出了一种大规模交通系统状态预测的深度学习架构,并在大规模数据集上验证了其有效性。Zhang等人[9]通过改进Dempster-Shafer 证据理论,提出了一种融合多源交通数据的实时城市交通状态估计方法,他们使用广州路网的环路检测器数据、摄像机数据和GPS 数据对所提出的估计方法进行了验证。然而,数据驱动方法也存在一些缺点:首先,这类方法对历史数据的数量和质量要求较高,若历史训练数据不足或质量较差,则难以获得较好的估计效果;其次,机器学习方法需要进行大量的模型参数调整工作才能获得较高的准确性,这个过程需要花费大量的时间和资源;此外,该类方法缺乏可解释性,模型估计结果往往很难被解释和理解。
基于模型驱动的状态估计方法(模型驱动方法)依赖于物理交通流模型,它根据交通动力学的先验知识,并利用实时数据估计交通状态。与数据驱动方法相比,模型驱动方法无须依赖大量的历史数据,具有较高的解释性和可移植性。在众多的宏观交通流模型中,LWR模型[10-11]被广泛应用于交通状态估计[12-15]。该模型是一阶连续交通流模型,实际应用中往往通过Godunov方案[16]进行时空离散化。当采用三角形或梯形基本图并满足Courant-Friedrichs-Lewy(CFL)条件[17]时,该离散化模型被称为元胞传输模型(Cell Transmission Model,CTM)[18-19]。CTM 模型易于进行数值计算,特别是对于大规模交通网络进行模拟时,其计算效率非常高,且模型能够较好地模拟各种交通现象(如:激波、排队形成与消散等),因此被广泛应用于交通模拟与估计。当前,主流的CTM 模型一般要求元胞长度是统一的,这使得CTM 模型在实际工程应用中存在明显的局限性。例如在实际高速公路场景中,流量信息主要来源于ETC 门架,因而常对相邻门架(组成一个门架对)之间的路段进行元胞划分。对于任一个门架对间的路段,检测器(如:视频或雷达)分布点位往往是不均匀的,如果仅通过给定元胞的数量或长度来确定元胞划分,会导致检测器数据难以融合应用。本文针对该问题提出了一种元胞划分方法,该方法可以灵活地调整元胞长度与数量,在保证ETC 门架对间元胞长度统一的同时,使元胞边界靠近检测器点位附近,从而可以有效利用其观测数据。
然而,离散化的交通流模型(如CTM)对实际交通流进行了较大幅度的简化,使得模型预测的结果与实际情况存在一定的差异。针对模型自身存在的缺陷,国内外学者提出了将交通流模型与实际采集数据相结合,以提高交通状态估计精度。当前高速公路大规模监控和数据采集主要依赖于断面检测器,如:ETC 门架、收费站、稀疏的视频点位检测器等。因此,绝大多数高速公路交通状态估计的研究都使用固定检测器采集的断面数据(如:流量、速度、占有率等)。龙科军等人[20]利用高速公路主线流量检测站和收费站的出入流水数据,针对交通流检测数据缺失、数据颗粒度粗、部分检测参数不完备等问题,提出了一种简易的交通流拥堵状态评估方法。Chen 等人[21]提出了旅行时间估计和预测框架,并利用台湾高速公路的公开电子收费数据评估模型的效果。陈喜群等人[22]提出了决策级融合模型(Squared Flow Error Bound-Extended Kalman Filter,SFEB-EKF),估计全路段交通状态,并采用最近邻法计算检测器不足环境下的全路段交通状态估计误差下界。符旭等人[23]基于拓展卡尔曼滤波提出了基于分布式车辆速度检测信息的城市快速路交通状态估计方法,并在PeMS 和MobileCentury 两个交通数据集上进行了有效性验证。然而,由于检测器部署较为稀疏且不均匀,仅依靠它们提供的稀疏断面数据,往往很难实现准确可靠且时空连续的交通状态估计。近年来,第三方互联网出行平台,如:高德、百度等导航服务提供商以及网约车公司等,利用其平台车辆的运行轨迹信息(位置、速度等),可以估算路段交通状态(如:平均速度)。由于该平台获得的只是道路上的样本车辆数据,因此无法估计交通流量或交通密度等状态信息。
为了解决当前高速公路主流数据源稀疏、时空不连续等导致的交通状态估计准确性和精细化程度不高问题,本文提出了一种融合多源数据和CTM 模型的高速公路交通状态估计方法。其中,实际交通数据源除了断面检测器的流量数据外,我们还采用了探测车辆(如:高德数据)提供的路段平均速度信息。本研究的主要工作和贡献在于提出了一种新的元胞划分方法,解决了CTM 模型在实际工程应用中要求元胞长度必须统一的限制;应用卡尔曼滤波技术将分布不均匀且稀疏的视频点位流量数据以及探测车辆平均速度数据与CTM 模型融合,准确估算高速公路路段各个栅格(元胞)内的车辆数(交通密度)、平均速度等,从而实现对高速公路的精细化交通状态估计。
1 交通状态估计模型构建
1.1 CTM模型
CTM[14-15]是LWR(Lighthill,Whitham and Richards)宏观交通流模型的一种离散化形式。相对于LWR 模型,该模型能更准确地描述交通流动力学特性,如激波、排队形成与消散等。在CTM 模型中,道路被划分为一系列长度相等(Δx)的元胞,时间被划分为相等时间步长(Δt)的时段。在每个时间步长内,元胞中的车辆数只受到其相邻元胞的影响。
为了确保数值计算的稳定性,元胞长度(Δx)和时间步长(Δt)之间需要满足离散化稳定性条件,即:νfΔt<Δx。该条件称为Courant-Friedrichs-Lewy(CFL)条件[17]。其含义是,在自由流状态下,标准车辆在一个时间步长内行驶的距离不得大于元胞的长度。CTM 设定流量-密度服从梯形基本图关系,如图1所示。

图1 梯形基本图Fig.1 Fundamental diagram
CTM 模型主要分为基本路段模型和节点模型,其中,节点模型包括分流节点和合流节点模型,如图2所示。接下来,分别对不同路段类型的CTM模型进行介绍。

图2 分路段示意图Fig.2 Different road structures
1.1.1 基本段模型
假设仿真时间间隔为Δt,则元胞更新的数学递推关系为:
式中:i表示元胞编号,i-1 和i+1 分别表示元胞i的上游和下游相邻元胞的编号;ni(t)和ni(t+Δt)分别表示t和t+Δt时刻元胞i上的车辆数(单位:标准车当量数,Passenger Car Unit,下文简称pcu);yi(t)和yi+1(t)分别表示t时刻,从元胞i-1流入元胞i和从元胞i流入元胞i+1 的车辆数(单位:pcu)。
基本路段上两相邻元胞之间车流传输的数学关系表达式为:
式中:ni-1(t)表示t时刻元胞i-1上的车辆(单位:pcu);k表示交通流密度(单位:pcu/km);Qc表示通行能力(单位:pcu/h);ω表示反向波传播速度(单位:km/h);νf表示自由流速度(单位:km/h);kj表示阻塞密度(单位:pcu/km);Δx表示元胞长度(单位:km)。
基本路段车流传播主要分为两部分,元胞发送Si-1(t)和元胞流入Ri(t),表达式如下:
式中:Si-1(t)为元胞i-1 在t至t+Δt时段内的发送函数,表示在该时段内元胞i-1 能够流出的最大车辆数(单位:pcu);Ri(t)为元胞i在t至t+Δt时段内的接收函数,表示在该时段内元胞i能够接收的最大车辆数(单位:pcu)。
1.1.2 合流段模型
交通合流情况下,下游元胞i会同时接收上游元胞i-1 以及入口匝道元胞j发送的车辆,如图2(b)所示。根据实际接收能力Ri(t)是否满足需求,合流段CTM模型可以分为以下两种情形:
(1)Ri(t)≥Si-1(t)+Sj(t)
此情况下,元胞i具有足够的接收能力,来自上游元胞和入口匝道元胞的需求都能被满足。此时,元胞i在t至t+Δt时段内的车辆流入数由上游元胞与匝道元胞共同决定,表达式为:
式中:yi-1,i(t)和yj,i(t)分别表示t至t+Δt时段内,由元胞i-1 流入元胞i和由入口匝道元胞j流入元胞i的车辆数(单位:pcu);Si-1(t)和Sj(t)分别表示t至t+Δt时段内元胞i-1 和入口匝道元胞j的发送函数(单位:pcu)。
(2)Ri(t) 此情况下,元胞i的剩余容量无法满足上游元胞i-1与入口匝道元胞j的总需求。此时,车流传输应满足: 式中:mid代表按大小顺序取三者的中间值;pi表示入口匝道汇入主干道的车流比。pi表示合流的优先级,当pi=0 时,上游主路的元胞i-1 相较于入口匝道元胞j具有优先通行权,下游主路的元胞i的接收量即为上游主路的元胞i-1 的发送量;反之,当pi=1 时,入口匝道元胞j具有优先通行权,下游主路的元胞i的接收量即为入口匝道元胞j的发送量。 当下游的元胞i的接收能力不能满足上游和入口匝道元胞的交通需求时,将会导致上游或入口匝道元胞的拥堵。在此情况下,上游元胞i-1和入口匝道元胞j流出车辆数将取决于两者的车流比pi。 1.1.3 分流段模型 交通分流情况下,元胞i发送的车辆yi(t)会同时流向下游元胞i+1 与出口匝道元胞j′,如图2(c)所示。yi(t)的值应该不大于元胞i的发送函数Si(t),元胞i+1 的接收车辆数yi,i+1(t)应不大于接收函数Ri+1(t),元胞j′的接收车辆数yi,j′(t)应不大于接收函数Rj′(t): 式中:po表示出口匝道流出主干道的车流比;yi,i+1(t)和yi,j′(t)分别表示t至t+Δt时段内由元胞i流入元胞i+1 和由元胞i流入元胞j′的车辆数(单位:pcu);Si(t)为t至t+Δt时段内元胞i的发送函数(单位:pcu);Ri+1(t)和Rj′(t)分别为t至t+Δt时段内元胞i+1和元胞j′的接收函数(单位:pcu)。 目前国内高速公路系统部署的断面检测器主要涉及ETC 门架、收费站和部分视频检测器,此外第三方互联网出行平台可以提供基于样本车辆数据的速度信息(如:路段平均速度等)。因此,本文提出了卡尔曼滤波框架下融合多源数据(如:视频流量、样本车辆平均速度)和CTM模型的交通状态估计方法,其框架如图3所示。针对高速公路实际场景,利用ETC 门架流量、速度数据标定路段基本图,同时考虑分、合流点位置等道路基础结构和视频检测器布设信息,将门架对间的路段划分为多个元胞,完成模型初始化;随后,基于卡尔曼滤波对多源数据进行融合,更新元胞状态;最后输出元胞级实时交通状态估计结果。后续章节分别对视频流量数据融合和速度数据融合模型进行详细介绍。 图3 融合多源数据和CTM的交通状态估计模型框架Fig.3 Framework of CTM-based traffic state estimation considering multi-source data 1.2.1 视频检测器流量数据融合 由于国内高速公路视频检测器的分布普遍较为稀疏且不均匀,本文提出了一种特定的元胞划分方法,在元胞长度统一的前提下,通过调整元胞数量与长度充分利用视频检测器流量数据。假设门架对之间存在s个视频点位Ρ1,…,Ρs,具体划分方法如下: 式中:X为门架对间道路长度,m;m为门架对间元胞数量,个;xΡn为视频点位n到路段入口门架的距离,m;D为给定的距离范围,m。 式(9)~(12)为考虑道路自由流速度、数据集计频率、视频点位分布,以元胞长度最小为目标建立的线性规划方程。式(9)要求元胞长度与数量之积等于门架对间的路段长度;式(10)要求元胞长度满足离散化稳定性条件;式(11)、(12)中,MΟD为取余操作,该部分保证了S个视频点位到最近的元胞边界的距离小于给定距离范围D。在方程无最优解的情况下,可以考虑适当减少应用的视频点位数量以减少约束条件,从而得到满足条件的最小元胞长度。 在上述线性规划方程存在最优解的情况下,视频点位Ρn到最近的元胞边界xi的距离均满足此时,元胞边界xi相邻的上游元胞i的发送函数Si(t),元胞边界xi相邻的下游元胞i+1 的接收函数Ri+1(t),以及t至t+Δt时段内由元胞i流入元胞i+1 的车辆数yi+1(t)可修改为: 式中:nΡn,i+1(t)为t至t+Δt时段内视频检测器Ρn测得的车辆数(单位:pcu)。 1.2.2 速度数据融合 卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统的输入输出观测数据,对系统状态进行最优估计的算法[24]。该技术主要用于处理带有噪声的数据,提高状态估计的准确性。在交通状态估计中,卡尔曼滤波与交通流模型相结合,对来自不同检测器的交通流数据(如:流量、速度)进行融合,能够得到准确、可靠的实时交通状态估计。标准的卡尔曼滤波模型主要包括状态转移方程和观测方程。本研究中,CTM 模型用于描述元胞的状态转移方程,计算元胞密度的估计值。同时,以路段平均速度(如:互联网出行平台提供的平均速度数据)作为实际观测量,应用基本图关系将其转换为观测密度,建立元胞密度估计值和观测密度之间的关系方程,即观测方程。随后,计算卡尔曼增益并对状态以及方差进行更新。 (1)状态转移方程 基于元胞传输模型,对任意元胞i,其密度变化与接收车辆数yi(t)和发送车辆数yi+1(t)有关,状态方程如下: 式中:t表示状态更新起始时刻(单位:h);Δt表示时间步长(单位:h);ki(t)表示t时刻元胞密度(单位:pcu/km);yi(t)和yi+1(t)分别表示t时刻,从元胞i-1 流入元胞i和从元胞i流入元胞i+1 的车辆数(单位:pcu)。 其中,误差方差的先验估计值计算如下: 式中:pi(t|t)为t时刻方差;Qi(t)为过程噪声方差。 对于所有元胞,状态转移方程以及方差更新公式可以写成向量的形式: 式中:Ν为元胞的总数量。 (2)观测方程 实际观测数据主要包括各种检测器获得的交通流数据,如:流量、速度等。本研究中,除了断面流量数据外,可通过互联网出行平台获得样本车辆的空间平均速度信息,并通过基本图关系得到密度信息。因此,t+Δt时刻的观测方程可表述如下: 式中:kio为基于基本图转换得到的元胞i的观测密度(单位:pcu/km);hi为测量方程系数;ξi为测量噪声,假设为高斯白噪声(单位:pcu/km)。 对于所有元胞,观测方程可以写成向量的形式: (3)状态更新随后,计算卡尔曼增益系数并更新状态方程,得到更新后的状态估计(密度),并更新元胞发送车辆数: 式中:K(t+Δt)为t+Δt时刻的卡尔曼增益矩阵;HT(t+Δt)为测量方程系数矩阵的转置;R(t+Δt)为测量噪声方差矩阵。 式中:I为单位矩阵;P(t+Δt)为t+Δt时刻的方差矩阵。 为了验证本文提出的MD-CTM估计模型的有效性,使用VISSIM 仿真软件构建了包括高速基本段、合流段和分流段的仿真场景。MD-CTM 模型通过路段输入、输出的车辆数(边界条件)和开始时刻路段内的车辆数(初始条件),预测路段内各个元胞的状态,然后基于卡尔曼滤波方法,利用观测的速度数据(如:探测车平均速度),对预测结果进行修正,将修正后的结果作为最终估计结果。基于标准CTM 模型的估计方法则仅利用边界条件和初始条件数据,估计路段各个元胞的状态,并将其作为最终状态估计结果。将MD-CTM模型估计结果、CTM 模型估计结果和VISSIM 仿真结果(基准)进行比较,对估计效果进行定性和定量评价。此外,选择四川省成都市G4202高速K49.35—K52.35 拥堵常发路段作为实际场景,进一步验证提出的MD-CTM 估计模型在实际应用中的可行性。 本文构建了长度为5 km 的单向双车道高速路段。该路段包含一个入口匝道,一个出口匝道以及两个视频检测点位,具体的道路结构如图4 所示。设置估计步长为15 s,将路段划分为多个元胞,每个元胞的长度为500 m。在整个路段中,包含了8 个基本段元胞、1 个合流元胞和1 个分流元胞,具体的元胞分布情况如图5 所示。此外,设置了四种流量情况,如表1所示。 表1 仿真流量设置Tab.1 Traffic flow settings in simulation 图4 路段构造示意图Fig.4 Road structure 图5 路段元胞划分示意图Fig.5 Cells distribution 基于流率、密度和平均流速的广义定义[25],使用仿真车辆轨迹数据进行基本图的标定,以获得流量-密度基本图。具体来说,基于仿真车辆轨迹数据时空图得到时空域A的面积,即时空图中由时段ΔT和距离dx围成的长方形的面积A,即时空图中时空域的面积A为: 广义的流率q定义为区域A中共计Ν辆车的行驶距离总和除以时空域A的面积: 式中:Δdi为车辆i的行驶距离。 广义的密度k定义为区域A中共计Ν辆车的行驶时间总和除以区域A的面积: 式中:x′(t)是车辆轨迹曲线的导数,即车辆在t时刻的瞬时速度。 在梯形基本图中,当元胞密度处在[0,k1]范围内时,梯形基本图的斜率为定值,元胞的空间平均速度恒为自由流速度νf,在实际应用中无法准确描述低密度状态下交通流速度的变化。在考虑应用简便性与有效性的基础上选择使用Smulders 基本图,其流量Q与密度k关系如下所示: 式中:Q表示流量(单位:pcu/h);νf表示自由流速度(单位:km/h);k表示交通流密度(单位:pcu/km);kc表示关键密度,在此密度下路段流量Q达到最大值(单位:pcu/km);kj表示拥堵密度(单位:pcu/km)。 依据式(25)~(27)所述方法处理车辆轨迹数据得到密度-流量数据,然后基于密度-流量数据使用最小二乘法标定该路段主路的基本图参数,结果如表2所示。 表2 路段基本图参数Tab.2 Parameters of fundamental diagram 为了量化分析本文提出的MD-CTM 模型与CTM 模型的估计性能,选取元胞密度和速度的平均绝对误差(Mean Absolute Error,MAE)作为评价指标,计算公式如下: 式中:n为元胞总数(单位:个);L为时间步总数(单位:步);kl,i为仿真中元胞i在第l步时的密度(单位:pcu/km);为估计模型得到的元胞i在第l步时的密度估计值(单位:pcu/km);νl,i为仿真中元胞i在第l步时的空间平均速度(单位:km/h);为估计模型得到的元胞i在第l步时的空间平均速度估计值(单位:km/h)。 为了进一步分析MD-CTM 模型相对于CTM模型在交通状态估计方面的改进程度,定义了两个评价指标,元胞密度误差降低百分比和速度误差降低百分比,公式如下: 表3 给出了不同流量情况下MD-CTM 模型和CTM 模型的估计效果对比。从表3 的结果可以看出,在1 000~3 000 pcu/h 流量范围内,随着主路流量的增大,CTM 模型和MD-CTM 模型的元胞密度估计误差均逐渐增大。相较于CTM 模型,MDCTM 模型在不同流量下的元胞密度估计误差更小,其误差降低百分比范围在12.53%~26.26%之间。同时,CTM 模型与MD-CTM 模型估计得到的元胞空间平均速度与VISSIM 仿真数据(基准)相比,误差较小,在3.325 km/h至4.055 km/h之间。 表3 估计效果对比Tab.3 Precision comparison 当主线交通流量较大(4 000 pcu/h)时,入口匝道的合流车辆对主路车流产生了较大的影响,导致汇流路段上游主路发生拥堵。从表3可以看出,MD-CTM 模型仍具有更好的估计效果,元胞密度估计误差相较于CTM 模型,降低了36.26%,速度估计精度提升28.33%。这表明,本文提出的模型能够有效利用了多源数据的优势,明显提升了交通状态的估计精度。 图6(a)~(d)展示了不同流量下基于VISSIM仿真数据、CTM 模型和MD-CTM 模型的密度时空图。在实际交通流运行中,流量的传递并不是完全均匀的。在数据时间颗粒度较粗的情况下,CTM 模型虽然能模拟出交通流动力学特性,但无法捕捉交通流随机性和变动性,因此其时空状态估计结果体现为连续性和均质性,其中图6(c)和(d)较为明显地体现了这一现象。本文提出的MD-CTM 估计模型融合了多源数据,在一定程度上考虑了交通流的随机变动性,从而更好地刻画了交通流运行状态。 当主线流量较大(4 000 pcu/h),接近通行能力时,入口匝道车流汇入导致合流元胞需求量超过了下游元胞通行能力,车辆在合流元胞堆积形成拥堵并往上游传播如图6(d)所示。虽然CTM 模型和MD-CTM模型均能较好地反映交通流状态变化特性(如:汇流导致的交通拥堵传播),但MDCTM 估计模型融合了路段速度和流量数据,能够更好地体现由于交通流随机变动性导致的交通状态变化不均匀性。 为了展示模型在实际场景中的估计效果,选择四川省成都市G4202高速的拥堵常发路段K49.3—K52.35。该路段主路为单向三车道,同时包含一个上匝道、一个下匝道,具体结构示意图如图7所示。选取时间步长为15 s,元胞长度为600 m 进行时空离散化。空间离散后的路段包含四个基本段元胞以及一个分合流元胞,该元胞同时包含一个入口匝道与一个出口匝道,如图8所示。 图7 试点路段道路结构示意图Fig.7 Road structure diagram of selected road 图8 试点路段元胞划分示意图Fig.8 Cell distribution diagram of selected road 获得数据主要包括出入口ETC 门架流量与速度数据,收费站进出流量数据以及分栅格的空间平均速度数据,时间为2023 年3 月24 日0 时至22时。利用门架流量与速度数据,对基本图参数进行了标定,结果如表4所示。 表4 试点路段基本图参数Tab.4 Fundamental diagram parameters of selected road 应用本文提出的MD-CTM模型对试验路段的交通状态进行估计,得到密度的时空图如图9所示。 图9 MD-CTM模型估计的路段密度时空图Fig.9 Space-time diagram of traffic flow density based on the MD-CTM results 从图9 中可以看出,MD-CTM 模型的估计结果能够较好地反映试验路段早高峰时段(7:00~9:00)和晚高峰时段(17:00~19:00)的交通拥堵状态特性。拥堵从试验路段下游元胞4 向上游元胞传播。在平峰时段(9:30~16:00),由于入口匝道汇流对主线交通流产生影响,使得汇流元胞上游出现轻度拥堵。在晚上平峰时段(19:00~22:00),主线和入口匝道流量较小,拥堵消散。以上结果表明,本文提出的估计模型能够较好地描述试验路段交通状态的时空变化规律,有效反映了出、入口匝道车流对主线交通运行状态的影响。 准确、可靠的交通状态估计是实现高速公路有效管控的前提和基础。国内高速公路检测器的部署普遍较为稀疏且不均匀,如何合理高效地利用这些稀疏数据,提供较为精确可靠的交通状态估计是一个难点问题。本文首先针对传统CTM模型中元胞长度划分不灵活,难以适应实际工程应用的问题,提出了一种新的元胞划分方法,可以调整元胞长度和数量,以更好地利用不同检测器数据;应用卡尔曼滤波技术,建立了一种融合多源数据和可变元胞长度CTM 模型(MD-CTM)的交通状态估计方法;利用VISSIM 仿真和实际高速公路场景案例验证了方法的有效性。主要结论如下: (1)本文提出的MD-CTM 估计方法相较于传统CTM 模型,其估计精度在不同交通流状态下均有较大的提升。特别在交通需求量较高的主线路段出现拥堵情况时,本文提出的方法能够显著降低元胞速度和密度的估计误差,提升高速公路交通状态的估计精度。 (2)传统CTM 模型虽然能够模拟交通流动力学特性,但无法捕捉交通流随机性和变动性,因此其时空状态估计结果体现为连续性和均质性。本文提出的MD-CTM 估计模型融合了多源数据,在一定程度上考虑了交通流的随机变动性,从而能够更好地刻画交通流的时空运行特性。 然而,由于缺少真实的交通状态基准数据,在实际试验路段案例中本文没有开展模型估计精度的分析。未来的研究中,将进一步对本文提出的模型估计效果进行实证研究。此外,在模型方面,将进一步优化模型结构以便更好地适用于实际场景中的复杂交织路段。1.2 基于卡尔曼滤波的融合估计方法

2 案例分析
2.1 仿真场景设置




2.2 仿真结果分析
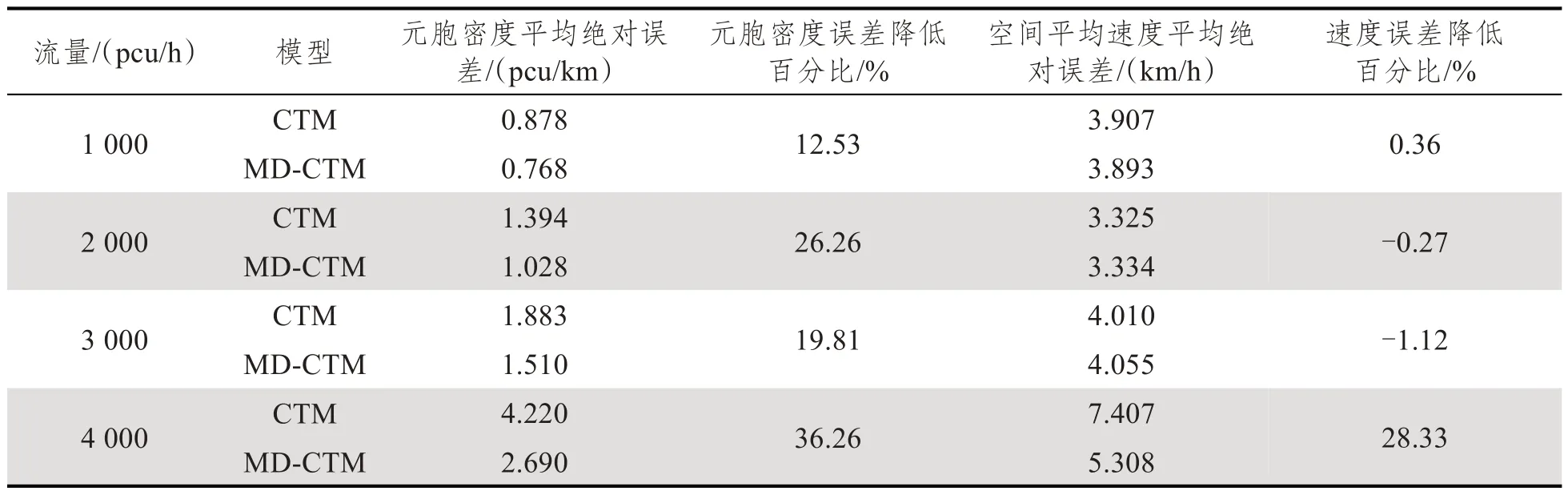
2.3 实际场景应用




3 结论
