统计场景创设 概率知识应用

张 恒

(淮安市洪泽湖高级中学,江苏 淮安 223100)

统计与概率的综合问题,是实际与应用场景的重要载体之一,已经成为新高考数学命题的重点．此类综合问题,以数据图表为场景,融合统计、概率或两者知识交汇中的基础知识与思想方法,利用统计场景加以创设,实现统计数据与统计信息的汇总,情境新颖,结合概率知识加以实际应用或判断决策,充分体现了统计与概率的工具性和交汇性[1]．

1 概率与频率分布直方图的综合

例1省会城市为了积极倡导市民优先乘坐公共交通工具绿色出行,在缓解交通压力与改善空间质量的同时,也倡导绿色理念,公共交通系统推出与之相关的一些便民服务措施．为了更好地了解人们对出行工具的选择,交管部门随机抽取了1 000人,做出统计表,详见表1.

表1 出行方式比例表

表2 出行频率概率

同时交管部门对某线路公交车统计整理了某一天1 200名乘客的年龄数据,得到的频率分布直方图如下图所示(图1):

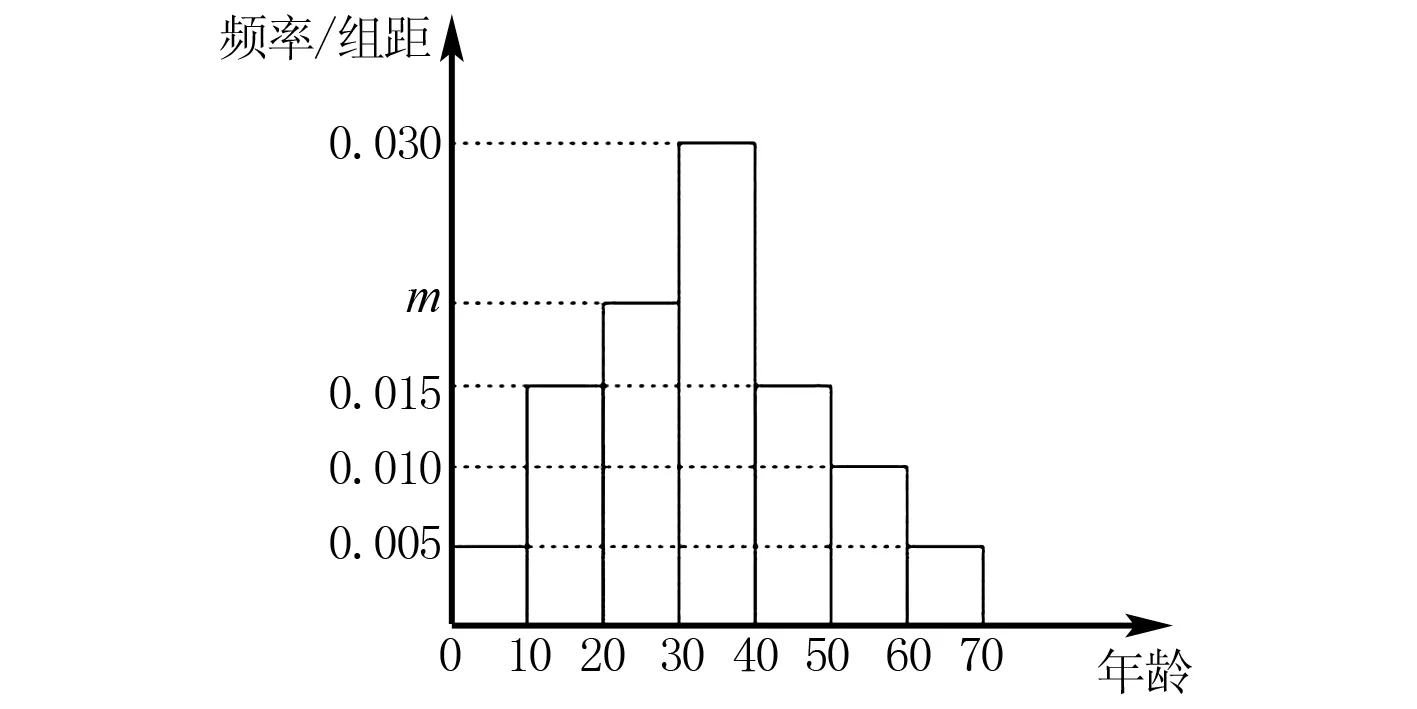
图1 频率分布直方图

(1)求m的值和这1 200名乘客年龄的中位数;

(2)用样本估计总体,将频率视为概率,从该市所有市民中抽取4人,记X为抽到选择公共交通出行方式的人数,求随机变量X的分布列和数学期望E(X)．

所以X的分布列为

点评涉及频率分布直方图的实际应用问题,关键就是正确识别与合理的数据读取.从中观察、读取相应的数据信息并对一些相关的数学加以合理汇总与应用,借此进一步综合概率知识来分析与计算,用于实际应用中的分析判断或信息决策[2]．

2 概率与独立性检验的综合

例2一种疫苗在正式上市之前要进行多次人体临床试验接种,假设每次接种互不影响,而且每人每次接种成功的概率相等．某医学研究院研究团队研发了一种疫苗,并率先对此疫苗开展了Ⅰ期和Ⅱ期临床试验．Ⅰ期试验为了解疫苗接种剂量与接种成功之间的关系,选取了两种剂量接种方案(0.5 mL/次剂量组(低剂量)与1 mL/次剂量组(中剂量)),临床试验免疫结果对比,详见表3.

表3 人体临床试验接种对比表

(1)根据数据分析说明哪种方案接种效果好,并判断是否有90%的把握认为该疫苗接种成功与否与两种剂量接种方案有关;

(2)若以以上表格中的数据的频率为概率,从两组不同剂量组中分别抽取1名试验者,以X表示这2人中接种成功的人数,求X的分布列和数学期望.

表4 随机变量观测值对照表

由2×2列联表得

所以没有90%的把握认为该疫苗接种成功与否与两种剂量接种方案有关．

所以X的分布列为

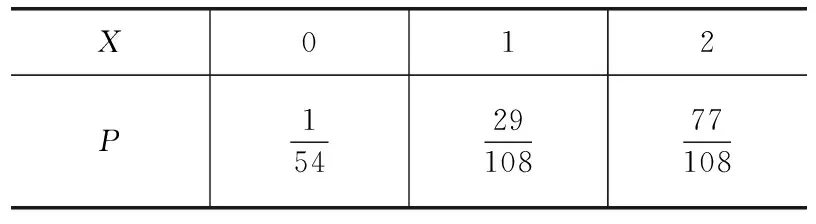
X012P1542910877108

点评在解决与独立性检验相关的概率与统计问题时,要从统计中的数据信息入手,结合独立性检验的公式计算与数据分析来判断与分析,并结合相应的统计、概率等基本知识,合理加以逻辑推理与数学运算,实现数据分析与实际应用．

3 概率与经验回归方程的综合

例3我国在芯片领域的短板有光刻机和光刻胶,某风险投资公司准备投资芯片领域,若投资光刻机项目,据预期,每年的收益率为30%的概率为p,收益率为-10%的概率为1-p;若投资光刻胶项目,据预期,每年的收益率为30%的概率为0.4,收益率为-20%的概率为0.1,收益率为零的概率为0.5．

(1)已知投资以上两个项目,获利的期望是一样的,请你从风险角度考虑,为该公司选择一个较稳妥的项目;

(2)若该风险投资公司准备对以上你认为较稳妥的项目进行投资,4年累计投资数据如下,详见表5.

表5 4年累计投资数据

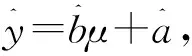
解析(1)若投资光刻机项目,设收益率为α1,则α1的分布列为详见表6.

表6 光刻机项目收益

所以E(α1)=0.3p+(-0.1)(1-p)=0.4p-0.1;若投资光刻胶项目,设收益率为α2,则α2的分布列为详见表7.

表7 光刻胶项目收益

所以E(α2)=0.3×0.4+(-0.2)×0.1+0×0.5=0.1;

因为投资以上两个项目,获利的期望是一样的,则有0.4p-0.1=0.1,解得p=0.5,

因为D(α1)=(0.3-0.1)2×0.5+(-0.1-0.1)2×0.5=0.04,

D(α2)=(0.3-0.1)2×0.4+(-0.2-0.1)2×0.1+(0-0.1)2×0.5=0.03,

所以E(α1)=E(α2),D(α1)>D(α2),

由于两个项目获利相等,但光刻胶项目更稳妥,则建议该风险投资公司投资光刻胶项目．

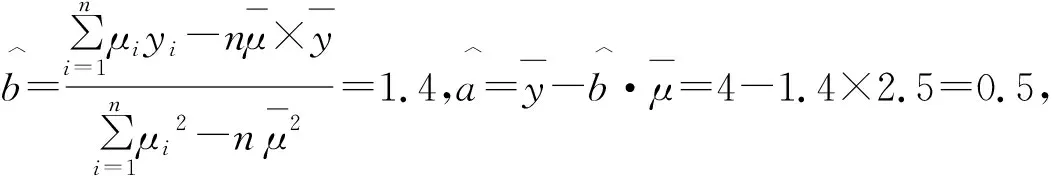
设该公司在芯片领域的投资收益为Y,则由Y=0.1×(1.4μ+0.5)≥0.75,解得μ≥5,

故到2023年年末,该投资公司在芯片领域的投资收益预期能达到0.75亿元．

巧妙地合理创设统计场景,借助概率知识加以实际应用,成为实际应用中考查的一个重要场景,有效考查考生的“四基”以及创新意识与创新应用,对于考生的数学能力的考查与数学核心素养的培养都有很大的指导意义．