中学生数学形象思维培养路径探究

魏靖函 邓方安

(陕西理工大学,陕西 汉中 723001)

随着社会科技的高速发展,培养高素质人才以适应社会需求成为教育的重要目标.数学作为基础学科,广泛应用到社会发展的方方面面,数学教育不仅能帮助学生掌握基础知识与基本技能,而且还能培养学生的思维能力.《高中数学课程标准》中明确提出,高中数学课程应注意提高学生的数学思维能力,数学思维的培养是数学教育的基本目标之一[1].数学思维分为数学抽象思维、数学形象思维以及数学直觉思维.其中数学形象思维作为数学思维能力的重要基石,对中学生数学思维能力的提升起着关键作用.

1 数学形象思维的概念

数学形象思维指以各种形象或表象为支柱的思考和解决数学问题的思维过程,以达到揭示数学问题本质的目的,从而进行创造性的教学活动.数学形象思维的基本形式包含:数学表象、数学联想和数学想象.数学表象是由数的形象、图形、图像、表格、表达式、数学符号、模型等观念形象在人脑中复现所形成的,主要呈现为图形表象和图式表象两种基本类型,它是数学形象思维的基本要素[2].数学联想是指以具体的数学表象为基础,联系头脑中已有的数学表象.数学想象是指通过数学联想将已有的数学表象加工成新的数学形象,使数学形象思维具有创造性的特点.

2 培养中学生数学形象思维的重要性

2.1 有助于提高中学生知识水平

法国著名数学教育家绍盖认为:一堆没有亲身体验或视觉形象所支持的概念定义之类的抽象的东西,不能开发智力,只能关闭思路.数学概念是进行数学推理和证明的依据,是数学学习的基础,因此数学概念的教学是数学教学中最重要的组成部分.数学概念是不会孤立存在的,任何数学概念一定是许多相互联系的知识网络上的一个点.数学形象思维可以加强知识之间的联系与相互转换,优化认知结构.例如,在学习多边形后可以建立如图1的知识网络体系,使学生感受数系的扩充和知识间的联系,有助于学生形成良好的概念图式[3].

图1 凸多边(角)形知识导图

2.2 有助于提高中学生学习积极性

数学作为基础学科不仅要提高学生的知识水平,还需调动学生学习积极性.但在大部分中学生眼中数学是极其抽象、复杂、单调的.因此很多中学生没有学习数学的兴趣,甚至讨厌数学.如果教师想提高学生学习数学的兴趣,打消学生对数学学科的偏见,重视学生数学形象思维的培养可以很好解决此问题.数学形象思维有助于中学生在头脑中对数学知识形成具体表象,便于理解与运用数学知识.例如在学习平行线的同位角、内错角时,从学生的实际生活情境出发,利用教室中存在的平行线:窗户的上下边框等,向学生展示生活中具体的同位角、内错角,不仅丰富了学生头脑中的数学表象,也提高了学生学习数学的兴趣,将数学与学生的实际生活联系起来.

2.3 有助于提高中学生解决数学问题的能力

数学问题的解决是中学阶段学生学习的重要内容.影响学生解决数学问题能力的因素有很多,如对知识、公式、定理的理解,问题解决的思路等.其中问题解决的思路是关键.数学家斯蒂恩认为:如果一个特定的问题可以被转化为一个图形,那么思想就整体地把握了问题,并且能创造性地思索问题的解法.可见把抽象的数学问题转化为直观的数学形象有助于解题思路的产生,如例1.

例1把表示同一平面内所有模不小于1且不大于2的向量的有向线段的起点移动到0点,则这些有向线段的终点所构成的图形面积等于多少?

分析此问题并不复杂,解决的关键就是把抽象的数学语言转化为数学形象.如图2,将同一平面内所有模等于1的向量的有向线段的起点移动到0点构成半径为1的圆,同理可知,模等于2的向量的有向线段的起点移动到0点构成半径为2的圆,画出图像,发现问题中的有向线段构成的图形是一个圆环.

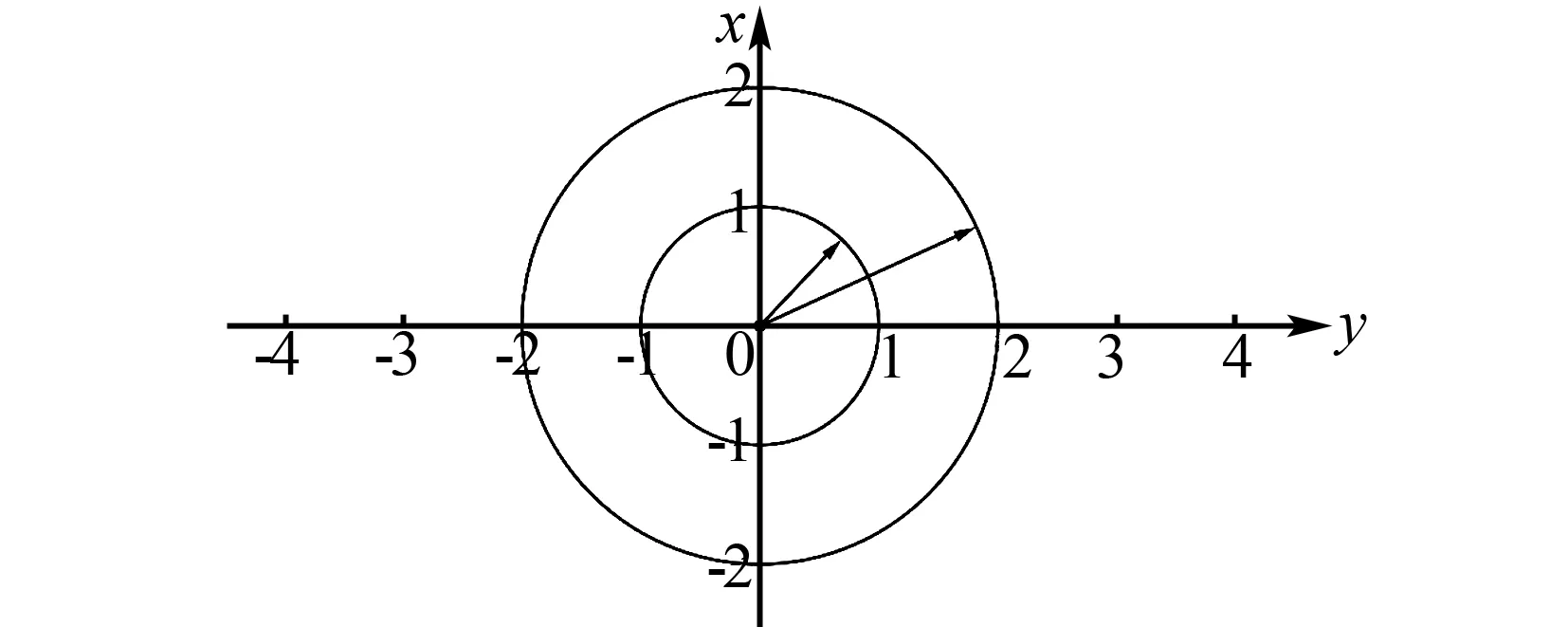
图2 向量图

解S=π·22-π·12=3π

3 中学生数学形象思维培养方法

3.1 加强直观演示,丰富数学表象

数学是一门较为抽象的学科,要解决数学高度抽象性与学生具体形象思维之间的矛盾,重要的是采取直观教学[3].研究发现,学生对知识的感知大多数来自于视觉刺激.在教学过程中教师需运用PPT、几何画板、GGB等软件,激发学生学习兴趣,丰富学生的数学表象.例如在学习直线与圆的位置关系时,运用几何画板如图3,直观展示直线与圆的三种位置关系:相交、相离、相切,丰富学生数学表象,促进数学形象思维能力的提升.

图3 直线与圆的位置关系展示图

3.2 创设情境,进行想象

爱因斯坦说:“想象比知识更重要,因为知识是有限的,而想象力概括着世界上的一切,推动着进步并且是知识进化的源泉.”想象是数学形象思维过程的一个重要环节,在教学过程中教师可以通过情境创设,丰富学生的形象能力.例如,函数的概念是高中函数学习的重要部分,由于函数概念具有高度的概括性和抽象性,脱离了学生的实际生活,使学生难以理解.因此在教学中,教师从丰富多彩的现实生活出发,展示“复兴号”列车路程和时间的关系,工资与一周工作天数的关系,以及一天内时间和空气质量指数的关系.由此引发学生想象:以上式子有什么特点,它们之间有共同特征吗?导入函数的具体概念以及本质属性.

思维定式是中学生数学学习的一种常见现象,是指学生按照已有的学习经验和思维方式,用某种固定的思维模式去思考和解决问题.思维定式可以帮助学生在解决同一类数学问题时,通过不断的练习和总结,使学生再面对此类型题时可以将其转化为熟悉的数学问题情境.思维定式也具有消极影响,学生形成思维定式之后在面对类似的问题时,不善于转变思维方式以多个角度去分析问题.因此,在数学解题的教学过程中教师可以打破常规,转化角度对问题进行思考,一题多解,培养学生的想象能力,促进数学形象思维能力的提高,如例2.

例2 等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?

分析本题首先通过已知条件确定数列是递增数列,解法一是常规解法,通过等差数列的公式解决问题.解法二是运用等差中项的性质,结合题目条件得出答案,不仅解题过程简单,还可加强学生综合运用数学知识的能力,促进数学形象思维的发展.

∵a1<0∴d>0,即等差数列{an}是递增数列.

解得10≤n≤11.

∴当n为10或11时,Sn取得最小值,

综上数列前10项或前11项的和最小.

∵a1<0∴d>0,即等差数列{an}是递增数列.

∵S9=S12,∴a10+a11+a12=3a11=0,∴a11=0.

∵数列{an}是递增数列,∴数列{an}前10项或前11项的和最小.

3.3 注重数形结合

我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”数形结合作为一种重要的数学思想方法,建立了形象思维和抽象思维之间的桥梁,把复杂抽象的数学语言与数学关系、直观的数学表象连接起来,促进中学生左右脑共同发展,如例3.

例3已知关于x的一元二次方程x2+2mx+2m+1=0,若方程有两实根,其中一根大于-1且小于0,另外一根大于1且小于2,求m的取值范围.

分析根据已知条件画出一元二次函数的图形是解决问题的关键.二次项系数大于零,则函数图象开口向上;一元二次方程有两个实根,则函数图象与x有两个交点,根据题目画出大概的函数图象,如图4.

图4 一元二次函数图

综上,数学形象思维作为中学生数学思维的重要基础,对中学生的数学学习尤为重要.在教学过程中,教师可通过加强直观演示,丰富中学生的数学表象;创设情境,提高学生的想象能力;注重数形结合来培养中学生数学形象思维能力.随着教育改革的不断深化,越来越多的人关注中学生数学形象思维能力的培养.数学形象思维作为中学数学的一种重要的思想方法,其有待研究之处还有很多,丰富数学形象思维思想方法的研究成果,不仅有助于学生自身的发展,也有利于数学其他方面的发展.