基于数值积分的器材供应保障数量决策建模
2023-12-12杜凯高崎刘志彬李朝阳史宪铭
杜凯 高崎 刘志彬 李朝阳 史宪铭
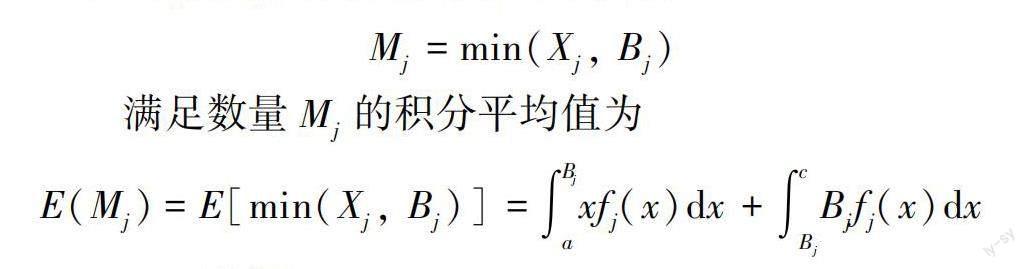
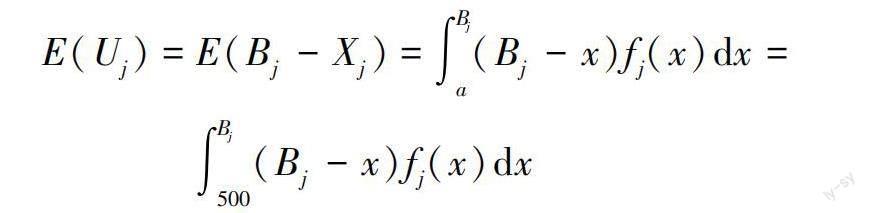
摘 要:随着部队编制体制改革的不断深入,部队装备呈现技术复杂化、种类多样化的特点,装备器材供应保障问题也日益凸显,研究如何满足装备器材使用需求的同时,最大限度提高保障效率,具有重要意义。在归纳总结国内外器材供应保障研究现状的基础上,提出部队亟待解决的现实问题,运用数值积分方法,从满足数量、短缺数量、冗余数量和误差数量四个方面建立数量决策模型,并通过Matlab进行编程求解,从而得出最优器材供应保障数量。最后结合事例,检验模型的准确性与实用性。
关键词:数值积分;simpson公式;标准决策;Matlab编程
中图分类号:E246文献标志码:ADOI:10.3969/j.issn.1673-3819.2023.06.004
Quantitative decision modeling of equipment supply guarantee
based on numerical integration
DU Kai1,2, GAO Qi1, LIU Zhibin2, LI Zhaoyang2, Shi Xianming1
(1. Shijiazhuang Campus of Army Engineering University, Shijiazhuang 050003, China;
2. Shijiazhuang Division of PLAA Infantry College, Shijiazhuang 050081, China)
Abstract: With the continuous deepening of the reform of the military organization system, the military equipment presents the characteristics of technical complexity and variety, and the issue of equipment supply and support is increasingly. It is of great significance to study how to meet the requirements of equipment use and maximize the efficiency of support. On the basis of summarizing the current research situation of equipment supply and support at home and abroad, this paper proposes practical problems which need to be solved urgently in the army. Using numerical integration methods, a quantity decision-making model is established from four aspects: satisfied quantity, shortage quantity, redundant quantity, and error quantity. The optimal equipment supply and support quantity is obtained through programming and solving with Matlab. Finally, an example is used to verify the accuracy and practicality of the model.
Key words:numerical integration; simpson formula; standard decision; Matlab programming
收稿日期:2023-03-13
修回日期:2023-04-16
作者簡介:
杜 凯(1991—),男,硕士研究生,讲师,研究方向为装备供应保障。
高 崎(1962—),男,博士,教授。
近年来,随着部队编制体制改革的不断深入,军队的规模结构和力量编成发生了革命性重塑,形成了军委管总、战区主战、军种主建的新格局,一体化联合作战机制体制日益凸显。部队合成化步伐不断加快,综合作战能力不断提升。与此同时,部队装备技术复杂化、种类多样化的特点也随之日益突出,对装备保障工作提出了更新更高的要求。器材保障作为实施装备保障工作的重要物质基础,逐渐成为战时装备保障研究的热点问题。
器材是指装备维修中所需元器件、零部件、附品、工具、军械油料、装护具、擦拭材料和原材料等的统称[1]。按照管理种类可分为配套器材、正常周转器材和战备储备器材[2]三种。其中正常周转器材一般以年度为基准,进行集中统一供应。对于器材需求预测问题,国内外学者做了大量研究,也建立了一些行之有效的数学模型,其大致可以分为四类:
一是基于数据统计方法,在历史统计数据的基础上,根据历史数据的变化趋势预测将来一段时间内器材的消耗量。其前提是在预测的这段时间内,影响器材消耗的主要因素不发生大的变化,且每类器材自装备服役以来的年实际消耗量和该类器材的年供应量等为已知。该方法使用范围广,主要有时间序列模型、回归分析模型、指数平滑模型、小样本模型、灰色预计模型、Bayesian模型、Croston模型、Bootstrap模型等,上述模型由于数据样本量的不同,标准计算的精度和结果有所不同[3],刘慎洋[4]基于军械装备使用及消耗分析,给出了军械器材消耗的常用模型及其消耗分布的获取方法,依据分段消耗规律给出了基于先验分布的军械器材消耗预测模型。崔亦斌[5]等针对二炮备件消耗标准制定问题,对影响备件消耗的因素进行分析,给出了单项备件的年度消耗标准以及战时备件的消耗标准模型。
二是基于寿命分布方法,该类模型建立在单元可靠性的基础上,从单元的损坏机理出发,依据单元在不同工作时间长度内发生故障的概率来预测备件在将来一段时间内的器材消耗量,备件保障度模型是其典型代表。Larry S.Mickel[6]提出寿命服从指数分布的可修备件需求量预计模型。夏长俊[7]提出寿命服从威布尔分布的可修备件需求量预计模型。
三是基于仿真预测方法,主要是在充分考虑部件消耗影响因素的基础上,做出一系列假设,运用系统仿真技术,建立装备和装备维修保障系统的仿真模型,模拟部件的使用、故障和维修过程,从而能够在最贴近实际的情况下得出部件消耗预测值。当前常用的建模方法主要有实体流图法、DEF3、Petri 网和ARIS法等。郭会军[8]等采用ARIS方法,对战时装备维修过程进行了分析,建立了战时备件需求的仿真模型。
四是基于成熟模型预测方法,主要有任务量预测法[9]、神经网络法[10]、灰色预测法[11]及支持向量机回归预测法[12]等。
以上方法均是从不同的角度采用不同的方法对器材进行了预测,呈现出多元化、多样化的特点,每种模型都存在一定的限定条件和使用范围,因此其预测模型的准确度和适用性也存在较大的差别。
1 问题描述
当前由于器材需求的随机性与供应保障的周期性的矛盾,导致部队有的器材积压严重,造成人力、物力和财力的极大浪费,并且器材的“保鲜”问题也随之突出。而有的器材供不应求,后续补充周期较长,造成了工作效率的大幅下降。目前已有的预测模型主要存在模型复杂、操作难度大等特点,缺乏一定的实用性。因此,寻求一种科学可靠、操作性强的方法,准确制定器材供应保障标准数量模型是当前部队维修保障亟须解决的一大难题。
本文基于寿命分布方法,在已知部队某器材需求规律的前提下,将器材供应标准数量与部队实际需求进行比较,采取simpson积分[13]的方式对其差值进行积分,并应用Matlab編程[14]进行求解,得到误差均值,通过使误差均值达到最小值,实现最大概率满足部队器材的保障需求。通过对建模和计算过程进行编程处理,大幅降低了复杂性,提高了对于部队的可操作性和实用性,进而最大限度减轻了器材积压和短缺两种矛盾问题对器材供应保障的影响。
2 假设与符号
2.1 基本假设
为了便于模型建立和求解,对装备器材作出如下假设。
1)装备器材适用于部队装备维修使用;
2)各单位装备器材不能调剂使用;
3)装备器材总体需求数量(分布)已知;
4)部队装备器材每年按装备器材标准补充一次。
2.2 数学符号
Xj:第j种装备器材年度需求数量,分布密度函数为fj(x)(已知);
Bj:第j种装备器材的标准数量(待求);
Mj:第j种装备器材满足数量(未知);
Qj:第j种装备器材短缺数量(未知);
Uj:第j种装备器材冗余数量(未知);
Dj:第j种装备器材误差数量(未知)。
3 模型建立
由于装备器材需求的随机性和装备器材标准的稳定性,在装备器材需求数量(实数)与装备器材标准数量(整数)之间总是存在不一致性,具体可用满足数量、短缺数量、冗余数量和误差数量来描述。
3.1 满足数量
装备器材满足数量是指按照装备器材标准进行装备器材保障,能够满足装备器材需求的数量。
第j种装备器材的满足数量为装备器材需求数量与装备器材标准数量之间的最小值。
Mj=min(Xj, Bj)
满足数量Mj的积分平均值为
E(Mj)=E[min(Xj, Bj)]=∫Bjaxfj(x)dx+∫cBjBjfj(x)dx
3.2 短缺数量
装备器材短缺数量是指按照装备器材标准进行装备器材保障,不能满足装备器材需求的数量。
第j种装备器材的短缺数量为装备器材需求数量与装备器材标准数量之差。
Qj=Xj-Bj(非负)
短缺数量Qj的积分平均值为
E(Qj)=E(Xj-Bj)=∫cBj(x-Bj)fj(x)dx
3.3 冗余数量
装备器材冗余数量是指按照装备器材标准进行装备器材保障,超出装备器材需求的数量。
第j种装备器材的冗余数量为装备器材标准数量与装备器材需求数量之差。
Uj=Bj-Xj(非负)
冗余数量Uj的积分平均值为
E(Uj)=E(Bj-Xj)=∫Bja(Bj-x)fj(x)dx
3.4 誤差数量
装备器材误差数量是指按照装备器材标准进行装备器材保障,保障的装备器材数量与需求数量之间差额的绝对值。
第j种装备器材的误差数量为装备器材需求数量与装备器材标准数量之差的绝对值。
Dj=|Bj-Xj|
误差数量的积分平均值为
E(Dj)=E(|Xj-Bj|)=E(Qj)+E(Uj)=∫Bja(Bj-x)fj(x)dx+∫cBj(x-Bj)fj(x)dx
4 优化方法
4.1 满足数量优化
拟制的装备器材标准应尽量满足装备器材需求,达到装备器材满足数量最大。即
max Mj=min(Xj, Bj)
通过调整装备器材标准Bj值,使目标函数取最大值。
4.2 短缺数量优化
拟制的装备器材标准应尽量减少装备器材短缺,达到装备器材短缺数量最小。即
min Qj=Xj-Bj
通过调整装备器材标准Bj值,使目标函数取最小值。
4.3 冗余数量优化
拟制的装备器材标准应尽量减少装备器材冗余,达到装备器材冗余数量最小。即
min Uj=Bj-Xj
通过调整装备器材标准Bj值,使目标函数取最小值。
4.4 误差数量优化
拟制的装备器材标准应尽量减少装备器材保障误差,达到装备器材误差数量最小。即
min Dj=|Bj-Xj|
通过调整装备器材标准Bj值,使目标函数取最小值即可得出最优供应标准数量。因解析求解过程过于复杂,所以利用simpson公式进行数值积分,并应用Matlab编程进行求解可得,短缺数量积分均值是关于标准数量Bj的一个单调不增函数,冗余数量积分均值是关于标准数量Bj的一个单调不减函数,因此无法求出最优解,而误差数量积分均值是关于标准数量Bj的单调递减而后单调递增的一个函数,因此存在最小值,可以求出最优解。
5 算例分析
对于已知需求规律的器材,其寿命分布主要为指数分布、正态分布和威布尔分布三种类型,求解不同器材的最优供应数量都可以采用此方法,只需将分布规律进行替换即可。下面,本文以服从威布尔分布的某型器材为例,运用此模型进行分析求解。
某合成旅修理连维修某型装备所需一种器材j,上级单位每年为合成旅供应一次此类器材,且此器材各部队之间不能调剂。已知该种器材的寿命分布服从k=10、λ=1 000的威布尔分布,上级供应数量上、下限为(500,1 000)。求解上级每年供应该种器材j最优数量。
由以上数据可知,器材j服从威布尔分布:
f(x)=kλxλk-1e-xλkk=10λ=1 000
a=500,c=1 000,并且Xj服从威布尔分布,其中k=10,λ=1 000,因此根据simpson公式,分别计算满足数量均值Mj、短缺数量均值Qj、冗余数量均值Uj及误差数量均值Dj可得:
E(Mj)=E[min(Xj, Bj)]=∫Bjaxfj(x)dx+∫cBjBjfj(x)dx=∫Bj500xfj(x)dx+∫1000BjBjfj(x)dx
由simpson数值积分,并用Matlab进行求解可得图1。
E(Qj)=E(Xj-Bj)=∫cBj(x-Bj)fj(x)dx=∫1000Bj(x-Bj)fj(x)dx
由simpson数值积分,并用Matlab进行求解可得图2。
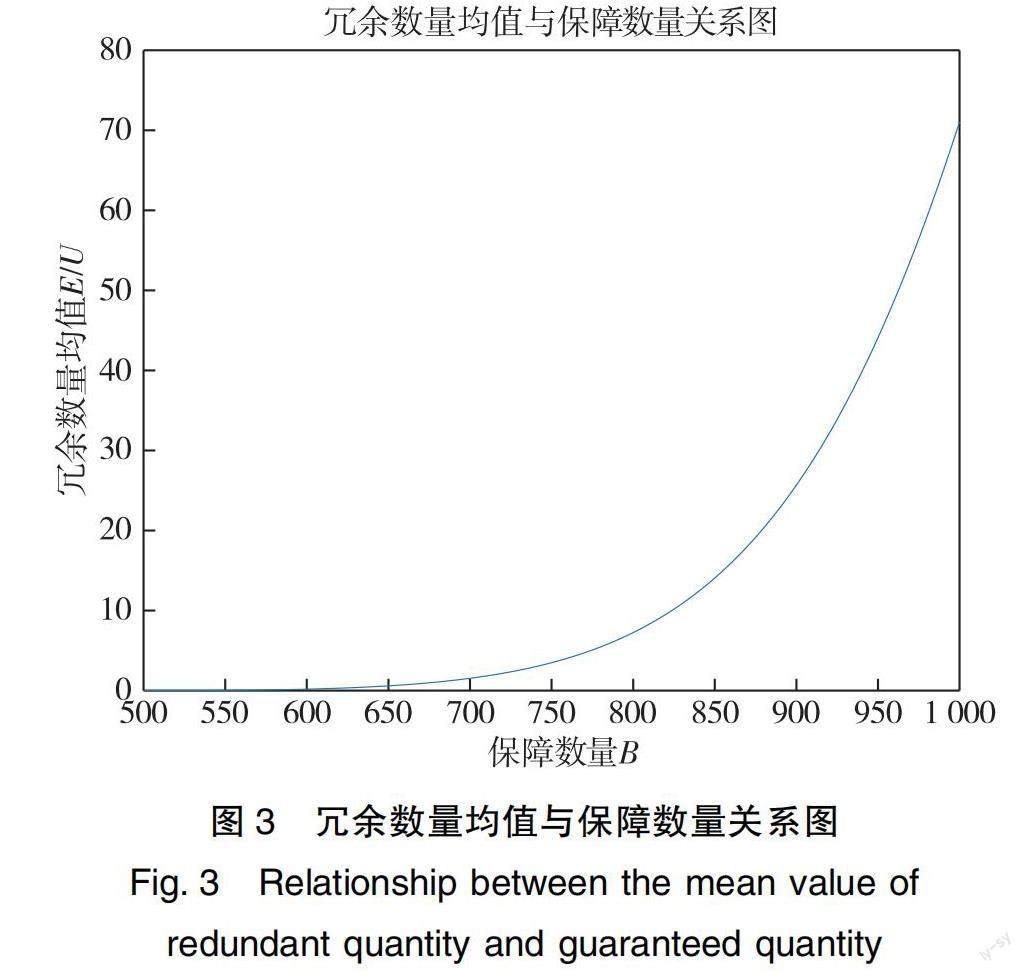
E(Uj)=E(Bj-Xj)=∫Bja(Bj-x)fj(x)dx=∫Bj500(Bj-x)fj(x)dx
由simpson數值积分,并用Matlab进行求解可得图3。
E(Dj)=E(|Xj-Bj|)=E(Qj)+E(Uj)=∫Bja(Bj-x)fj(x)dx+∫cBj(x-Bj)fj(x)dx=∫Bj500(Bj-x)fj(x)dx+∫1000Bj(x-Bj)fj(x)dx
由simpson数值积分,并用Matlab进行求解可得图4。
由图4可知,当Bj=908时,取得最小值,误差均值最小。
由此可以得出,当上级供应器材j的数量为908时,能够最大限度满足该部队对器材j使用需求的同时,也避免了因过量储存而造成库存积压和运力浪费等问题,为部队器材供应保障筹划工作提供决策依据。
6 结束语
本文通过simpson积分公式,对器材需求与供应保障之间的误差函数进行积分和建模,并运用Matlab编程对积分均值进行求解,从而得出最优解,即供应保障最大满足标准数量,为决策者科学制定供应保障标准数量,解决部分器材积压或短缺所带来的矛盾问题,提供了解决方法,并且可以针对不同的需求规律的器材分别进行求解,最大程度保证了部队器材供应与需求的精准对接。
参考文献:
[1] 高崎.军械器材管理术语及相关概念[M].北京:国防工业出版社,2016.
GAO Q. Ordnance equipment management terminology and related concepts[M]. Beijing:National Defense Industry Press, 2016.
[2] 高崎.军械器材管理学[M]. 北京:国防工业出版社,2012.
GAO Q. Ordnance management[M]. Beijing: National Defense Industry Press, 2012.
[3] 任博, 张恒喜, 苏畅. 基于支持向量机的飞机备件需求预测[J]. 火力与指挥控制, 2005, 30(3): 78-80, 83.
REN B, ZHANG H X, SU C. Requirement prediction of aircraft spare parts based on support vector machines[J]. Fire Control & Command Control, 2005, 30(3): 78-80, 83.
[4] 刘慎洋.军械器材消耗预测方法研究[D].石家庄军械工程学院硕士学位论文, 2015,12.
LIU S Y. Research on prediction methods of ordnance consumption[D]. Masters Thesis of Shijiazhuang Institute of Ordnance Engineering, 2015,12.
[5] 刘华安, 张兆新, 王悦岭. 二炮备件消耗标准制定分析[C]//第四届中国青年运筹与管理学者大会论文集. 2001: 460-466.
LIU H A, ZHANG Z X, WANG Y L. Analysis on the formulation of spare parts consumption standard for the second gun[C]//Chinese Youth Conference of Operational Research and Management Scholars, 2001:460-466.
[6] MICKEL L S, HEIM R L. The spares calculator: a visual aid to provisioning[C]//Annual Proceedings on Reliability and Maintainability Symposium. Los Angeles, 2002: 410-414.
[7] 夏长俊, 赵修平. 寿命服从威布尔分布的装备备件储备量确定[J]. 舰船科学技术, 2006, 28(4): 100-102.
XIA C J, ZHAO X P. Determinate the storage quantity of the equipments which life submit weibull distribution[J]. Ship Science and Technology, 2006, 28(4): 100-102.
[8] 郭会军, 刘伟. 基于ARIS的战时备件需求仿真模型研究[J]. 科学技术与工程, 2007, 23(7): 6257-6259.
GUO H J, LIU W. Simulation modeling study on spare parts demand in wartime based on ARIS[J]. Science Technology and Engineering, 2007, 23(7): 6257-6259.
[9] 李武胜. 电厂热工控制系统备件消耗预测研究[D]. 北京: 北京物资学院, 2009.
LI W S. The research on spare parts consumption forecasting of thermal control system in the electric power plant[D]. Beijing: Beijing Wuzi University, 2009.
[10]龙军, 康锐, 康晓明, 等. 基于综合效能参数的备件订货配置优化模型[J]. 系统工程与电子技术, 2007, 29(12): 2085-2087.
LONG J, KANG R, KANG X M, et al. Optimization of spares supply based on integrated supply performance measure[J]. Systems Engineering and Electronics, 2007, 29(12): 2085-2087.
[11]刘琼, 段亦彬. 基于灰色理论的火炮维修器材消耗预测模型[J]. 四川兵工学报, 2011, 32(1): 49-51.
LIU Q, DUAN Y B. Forecast model of apparatus consumption for artillery maintenance based on grey theory[J]. Journal of Sichuan Ordnance, 2011, 32(1): 49-51.
[12]牛余宝, 王晓坤, 赵艳华. 基于支持向量机的飞机备件消耗预测研究[J]. 长春大学学报, 2012, 22(6): 631-633.
NIU Y B, WANG X K, ZHAO Y H. Research on the prediction of aircraft spare parts consumption based on support vector machine[J]. Journal of Changchun University, 2012, 22(6): 631-633.
[13]呂同富, 康兆敏, 方秀男. 数值计算方法[M]. 北京: 清华大学出版社, 2008.
LYU T F, KANG Z M, FANG X N. Numerical computation method[M]. Beijing: Tsinghua University Press, 2008.
[14]周品. MATLAB数值分析应用教程[M]. 北京: 电子工业出版社, 2014.
ZHOU P. MATLAB numerical analysis application course[M]. Beijing: Publishing House of Electronics Industry, 2014.
(责任编辑:许韦韦)
