重复控制在三相不平衡负载中的应用
2023-12-11叶宗彬代金贵邓先明于东升
叶宗彬, 陆 超, 代金贵, 邓先明, 于东升
(1.中国矿业大学电气工程学院,江苏徐州 221116;2.国网山东省电力公司泰安供电公司,山东泰安 271000)
0 引 言
逆变器输出电压中除了基波分量,还含有一定的谐波。谐波主要来自PWM 调制产生的谐波、死区产生的谐波、逆变器带非线性负载所产的谐波。PWM调制产生的谐波主要分布在开关频率附近,可通过合理设置LC 低通滤波器的截止频率将其滤除。针对死区、不平衡负载、非线性负载等非线性因素产生的谐波,可采用比例谐振控制器。为抑制不同频率的谐波,需要一定数量的谐振控制器,导致控制系统结构复杂,增加了微控制器的计算负担,降低了工程应用价值。
为抑制各次谐波,可采用重复控制器。重复控制器在不同谐波频率处均具有很大的控制增益,可同时抑制各次谐波[1-3]。重复控制器结构简单,稳态时逆变器输出电压中谐波含量小,微控制器的计算负担小,所以在逆变器控制中得到了广泛应用。
1 重复控制器原理
重复控制的基本思想来自控制理论中的内模原理[4-5]。内模原理指出,对于一个闭环反馈系统,若系统的输出能跟踪外部输入的参考信号(即稳态时误差趋于零)且具有抵消扰动的能力,则控制环路内部必须包含有外部输入信号(含参考信号和扰动信号)的数学模型。外部输入信号的数学模型就是“内模”,内模原理本质是把外部输入信号的数学模型植入控制器,以构成高精密的反馈控制系统。
当参考信号为正弦信号时,根据内模原理,可在控制器中植入一个与参考信号同频率的正弦信号模型。但逆变器输出电压中不仅含有基波,还含有许多谐波分量。谐波分量的频率都为基波频率的整数倍,且在每一个工频周期内都以完全相同的波形重复出现。因此,可采用如下形式的内模(在s域的表现形式):
式中,T为逆变器输出电压基波周期。已有学者证明[6],式(1)可以写为:
式中,ωT为基波角频率。从式(2)可见,该内模包含了直流分量、基波分量和各谐波分量,理论上可实现对基波参考信号的无静差跟踪以及对谐波的抑制。
e-Ts为延迟环节,难以用模拟器件实现。随着逆变器控制数字化的发展,在微控制器中通过编程实现该延迟环节很容易。实际应用中的重复控制都是以数字化的方式实现的。通过z变换,可得该内模在离散域的表达形式
式中:N为每个基波周期内的采样次数(N=T/Ts,Ts为采样周期);z-N为延迟N个采样周期,意味着用微控制器实现该延迟环节需要留出N个存储单元。
重复控制结构如图1 所示,是具有一个工频周期延迟的正反馈环节[7-8]。其中,e(z)为参考信号与反馈信号的差值;y(z)为重复控制器的输出。当反馈信号与参考信号不相等时,输入信号e(z)不为零,重复控制器的输出会对输入信号进行逐周期累加,其作用与PI调节器中的积分环节相似。经过重复控制器的调节,输入偏差信号e(z)最终为0。此时,该内模会持续不断地重复输出上一周期的控制信号,因此称为重复控制器。
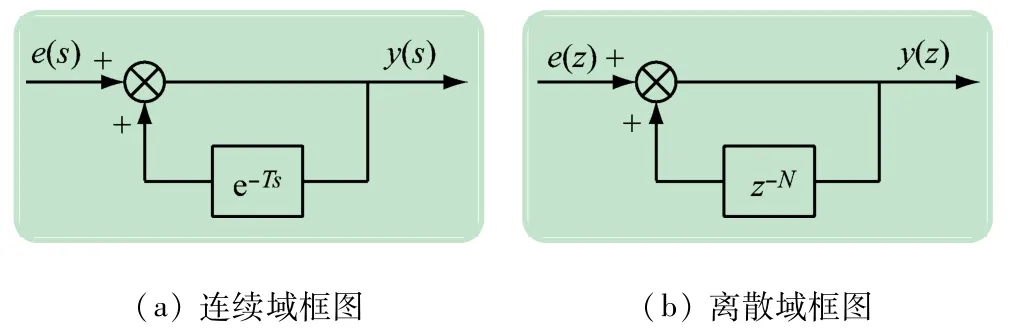
图1 重复控制结构框图
2 重复控制结构
基于重复控制的系统结构如图2 所示,由重复控制器的内模、延迟环节和补偿器组成[12]。r(z)为给定参考量,y(z)为系统的输出,e(z)为两者的差值。P(z)为控制对象,d(z)为系统的重复性扰动。Q(z)为低通滤波器或常数,z-N为周期性延迟环节,C(z)为补偿器,共同组成了重复控制器[9]。
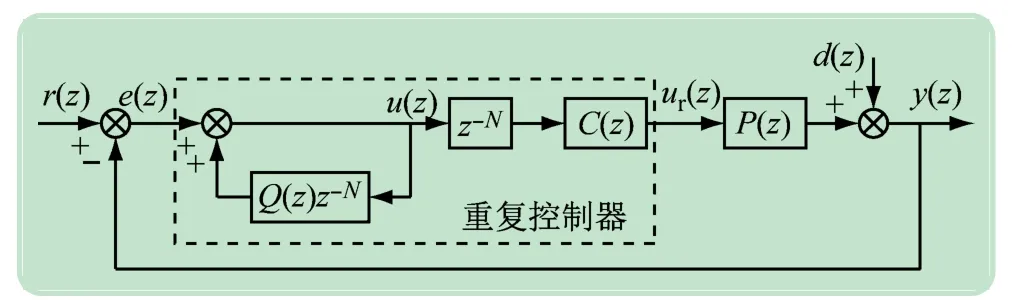
图2 基于重复控制的结构框图
(1)低通滤波器或小于1 的常数环节Q(z)。为提高系统的稳定性,通过加入Q(z)对重复控制器的内模进行改进,Q(z)可为低通滤波器或者小于1 的常数[10-11]。当Q(z)为低通滤波器时,输入信号中的高频分量会快速衰减,而低频分量衰减较慢。低通滤波器有相移,导致改进后的内模在基波以及基波频率的整数倍处增益降低。当Q(z)为小于1 的常数时,内模的幅值在整个控制频率范围内均衰减。改进后的内模,输入、输出之间的关系:
(2)周期延迟环节z-N。补偿器C(z)的构成中含有相位补偿的超前环节,前向通道串联延迟环节z-N使得相位补偿在仿真和微控制器中得以实现[12]。同时,为消除本周期所存在的误差,应施加一定的控制信号。延迟环节的存在,致使控制动作延迟了一个周期进行。参考信号和扰动都具有重复性,因此可使系统在下一个周期的控制具有一定的超前性。
(3)补偿器C(z)。重复控制器设计的关键在于补偿器,对重复控制器的性能产生重要影响[13-14]。补偿器C(z)为被控对象P(z)提供幅值补偿与相位补偿,以保证系统的稳定。采用超前环节实现相位补偿时,补偿器C(z)可以写为:C(z)=Kr·zk·S(z)。其中,Kr为补偿器的增益,取值范围一般为大于0 且小于等于1 的常数。增益越大,系统的动态响应速度越快,但系统的稳定性会减弱。因此,需要综合考虑系统对动态性能和稳定性的要求以选择适当的值。zk为相位补偿的超前环节,由于补偿器C(z)以及被控对象P(z)会引起相位滞后,通过加入相位补偿环节zk使得C(z)P(z)在中低频段相移为零[15]。S(z)为滤波器,其作用是:对被控对象P(z)进行幅值校正,使C(z)P(z)在中低频段的幅值为0 dB,在高频段幅值大幅衰减,以保证系统的稳定。若被控对象P(z)中有谐振峰,S(z)还需要抵消谐振峰,使之不破坏系统的稳定性。
3 重复控制器性能分析
(1)稳定性分析。根据图2,重复控制器输入、输出的关系
式中,e(z)=r(z)-y(z)=r(z)-ur(z)P(z)-d(z)为误差。
将误差e(z)代入式(5),经整理可得误差
由此可得引入重复控制器后的系统特征方程
特征方程N个根均位于以原点为圆心的单位圆内,则系统是稳定的。但特征方程的阶数一般是很高的。基波频率为工频50 Hz,采样频率为10 kHz时,特征方程的阶数为200。可利用控制理论中的小增益定理,得到系统稳定的充分条件
从零频率到奈奎斯特频率(采样频率的一半),只要Q(z)-C(z)P(z)在上述频段范围内其增益小于1,重复控制系统一定是稳定的。但该条件是稳定的充分条件而非必要条件,若不满足该条件系统也可能是稳定的。式(8)所描述的稳定性条件不够直观,通过图3展示稳定性的几何意义。为方便分析,令:

图3 稳定性的几何意义
当Q取小于1 的常数时,单位圆的圆心左移1 -Q,使得单位圆包含了第Ⅱ、Ⅲ象限的一部分,如图3(b)所示。即使C(z)P(z)的相角超出±90°,但只要C(z)P(z)在高频段的幅值足够小,矢量H(ejωTs)的末端轨迹仍位于单位圆内,系统依然保持稳定。当Q为低通滤波器时,单位圆的圆心随着频率的升高而左移。在低频段,单位圆的圆心很接近(1,0),由于补偿足够准确,可保证重复控制的稳定性。在高频段,单位圆的圆心左移,单位圆进入第Ⅱ、Ⅲ象限,只要C(z)P(z)在高频段增益足够小,系统仍可以保持稳定。
(2)抗干扰性能分析。根据图2,可得扰动信号作用下系统的闭环传递函数
设扰动信号的角频率为ωd,参考信号的角频率为ωr,若扰动信号的角频率为参考信号频率的整数倍,即ωd=kωr(k=1,2,…,N/2),则z-N=1。当采用理想内模,即Q(z)=1,式(10)变为:
式(11)表明,采用理想内模时,重复控制对于奈奎斯特频率以下的扰动信号可实现完全抑制。
而当Q(z)小于1 时,扰动信号衰减倍数
由式(12)可见,当采用非理想内模时,重复控制无法完全抑制扰动信号,而是衰减到原扰动信号幅值的倍。且Q(z)越接近于1,衰减倍数越多,重复控制对扰动的抑制能力越强。
(3)误差收敛分析。假设参考信号r(z)和扰动信号d(z)具有重复控制性,即每一个基波周期波形与上一个基波周期的波形完全相同。根据离散控制的滞后定理
对具有重复性的扰动信号,z-N=1。当采用理想内模时,即Q(z)=1,对式(6)整理可得:
式(14)表明,经过一个基波周期后,误差衰减为上个基波周期的H(z)倍。H(ejωTs)的模值越小,误差的衰减速度越快。由于H(ejωTs)为频率的函数,因此不同频率的谐波收敛速度不同。
(4)稳态误差分析。由式(6)可见,稳态误差由2部分构成,一部分是参考信号r(z)的跟踪误差,另一部分是扰动d(z)引起的误差。其中稳态误差的幅值
从式(15)可见,经重复控制器的调节后,稳态时无论是参考信号的跟踪误差r(ejωTs),还是周期性扰动引起的误差d(ejωTs),都将衰减为原来的
4 重复控制器设计
图2 所示的重复控制结构,由于重复控制器内模含有z-N,导致重复控制器的输出延迟一个基波周期。当突加参考信号或输出电压受到扰动时,重复控制无法快速做出响应,动态响应慢。可采用图4 所示的“嵌入式”重复控制结构,在使用重复控制器的基础上,进一步将参考信号进行前馈,提高系统的动态响应速度。

图4 “嵌入式”重复控制结构
重复控制器的设计主要包括:滤波器Q(z)、周期延迟环节z-N和补偿器C(z)。其中,最关键的是补偿器的选择以及参数设计。为保证系统的稳定,当重复控制器参数设计完毕,需对所设计的重复控制器进行稳定性校验。重复控制器的设计可按以下步骤进行:
步骤1 滤波器。Q(z)可为低通滤波器,也可以是小于1 的常数。本文将Q(z)的值设置为常数0.95。
步骤2 周期延迟环节。控制系统的采样周期Ts=0.1 ms,逆变器输出电压基波周期T=20 ms,则N=T/Ts=200,周期延迟环节为z-200。
步骤3 补偿器。两电平逆变器经LC 滤波器为负载供电时,逆变器的闭环传递函数
式中:滤波电感Lm=4 mH;滤波电容Cf=9.4 μF;滤波电感等效电阻Rm=0.5 Ω。将以上参数代入式(16),可得:
采用零阶保持器对被控对象P(s)进行离散化
由图5 被控对象的伯德图可以看出,逆变器在谐振频率821 Hz处,谐振峰值为32.3 dB。为消除谐振峰,同时使被控对象P(s)在高频段快速衰减,补偿器C(z)的滤波器S(z)可选用FIR数字滤波器,或者将二阶低通滤波器与零相移陷波滤波器级联组合使用。本文采用后者,零相移陷波滤波器只在谐振频率处拥有很强的衰减能力,用以抵消谐振峰,而不会对其他频率段的增益产生影响。二阶低通滤波器主要是增强被控对象P(s)在高频段衰减特性,其截止频率不必设置得太低。
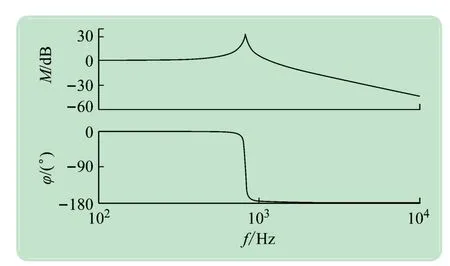
图5 被控对象P(s)的伯德图
在离散域的零相移陷波滤波器
S1(ω)在特定频率处产生较强衰减时,应满足
于是可得:
在频域的二阶低通滤波器
为实现对高频信号的衰减,二阶低通滤波器的阻尼比ξ≥0.707。本文阻尼比ξ 取为0.707,截止频率ωc设定在20 次谐波处,即6 283 rad/s,该二阶低通滤波器
对式(23)进行双线性变换,可得在离散域的二阶低通滤波器
故滤波器
图6 为S(z)P(z)的伯德图。被控对象P(z)经滤波器S(z)校正后,已无谐振峰,低频段的幅值基本为0 dB。中高频段,校正后的系统有较大的相位滞后,在频率为1 kHz处,相位滞后已经超过270°。为实现中低频段零相移,需要对其进行相位补偿。

图6 S(z)P(z)的伯德图
采用超前环节z3进行相位补偿,补偿后的伯德图如图7 所示。系统在中低频段的相位基本为0。在谐振频率处相位接近90°,校正后的系统在该频率处增益超过了-200 dB,依然可保证系统的稳定性。
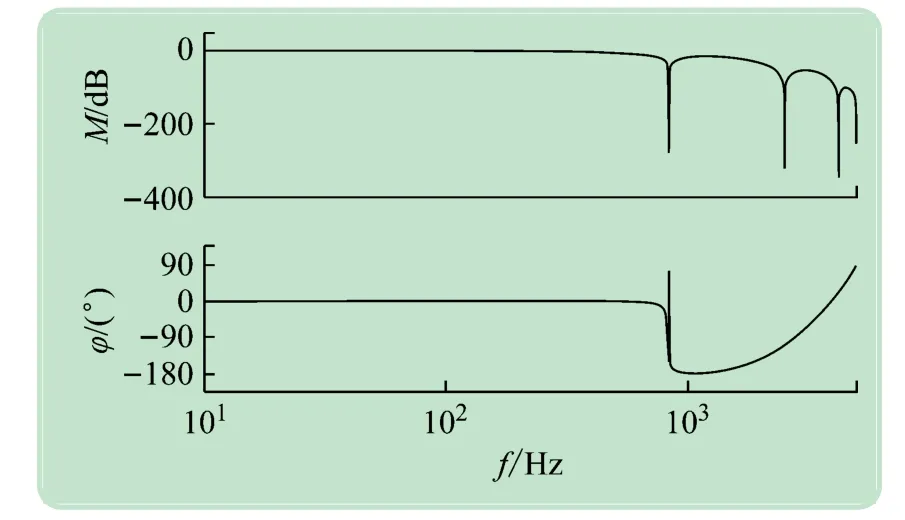
图7 z3S(z)P(z)的伯德图
采样以及PWM 环节存在延迟,也需对其进行补偿,最终超前环节选用z5。当补偿器的增益Kr取为1时,补偿器
稳定性校验。根据所设计的重复控制器,可得如图8 所示的Q(z)-C(z)P(z)的奈奎斯特图,从零频到奈奎斯特频率(采样频率的一半),Q(z)-C(z)P(z)的幅值均小于1,因此系统是稳定的,所设计的重复控制器参数满足稳定性要求。
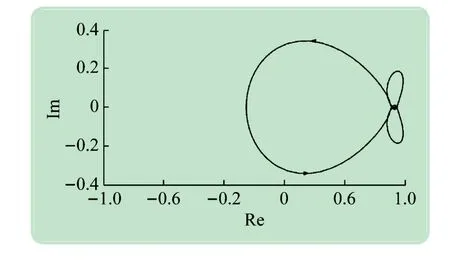
图8 Q(z)-C(z)P(z)的奈奎斯特图
5 仿真与实验验证
为验证控制策略的有效性,搭建实验平台,如图9 所示。信号处理电路由DSP +FPGA 构成,其中DSP芯片采用TMS320F28335,控制策略、过压过流保护均在该芯片中完成,FPGA 芯片采用SPARTANT6 XC6SLX9,用于PWM 控制信号的生成、电平保护逻辑、驱动电路的反馈信号检测。
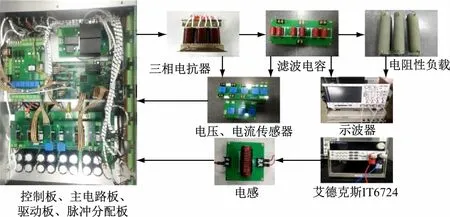
图9 实验平台组成
Simulink搭建的仿真与实验室条件下搭建的小功率实验平台参数相同,见表1。

表1 重复控制的仿真参数
逆变器采用双闭环前馈解耦控制策略,A 相负载20 Ω、B相与C相均为负载10 Ω,仿真波形如图10、11所示,实验波形如图12 所示。由图10 显见,A相电压幅值明显高于B、C 相。由图12 的实验波形可见,A相电压的有效值为32.8 V,B 相25.89 V,C 相26.78 V,逆变器输出的三相电压不再对称。由图11中可见,输出电压中含有正序分量和负序分量,无零序分量。正序电压分量经过Park变换后为直流量,负序电压分量经过Park 变换后为两倍频分量。由内模原理可知,传统PI控制器只能对直流量实现稳态无静差跟踪。经过电压、电流双闭环控制后,负序电压分量依然存在,导致三相电压不对称。
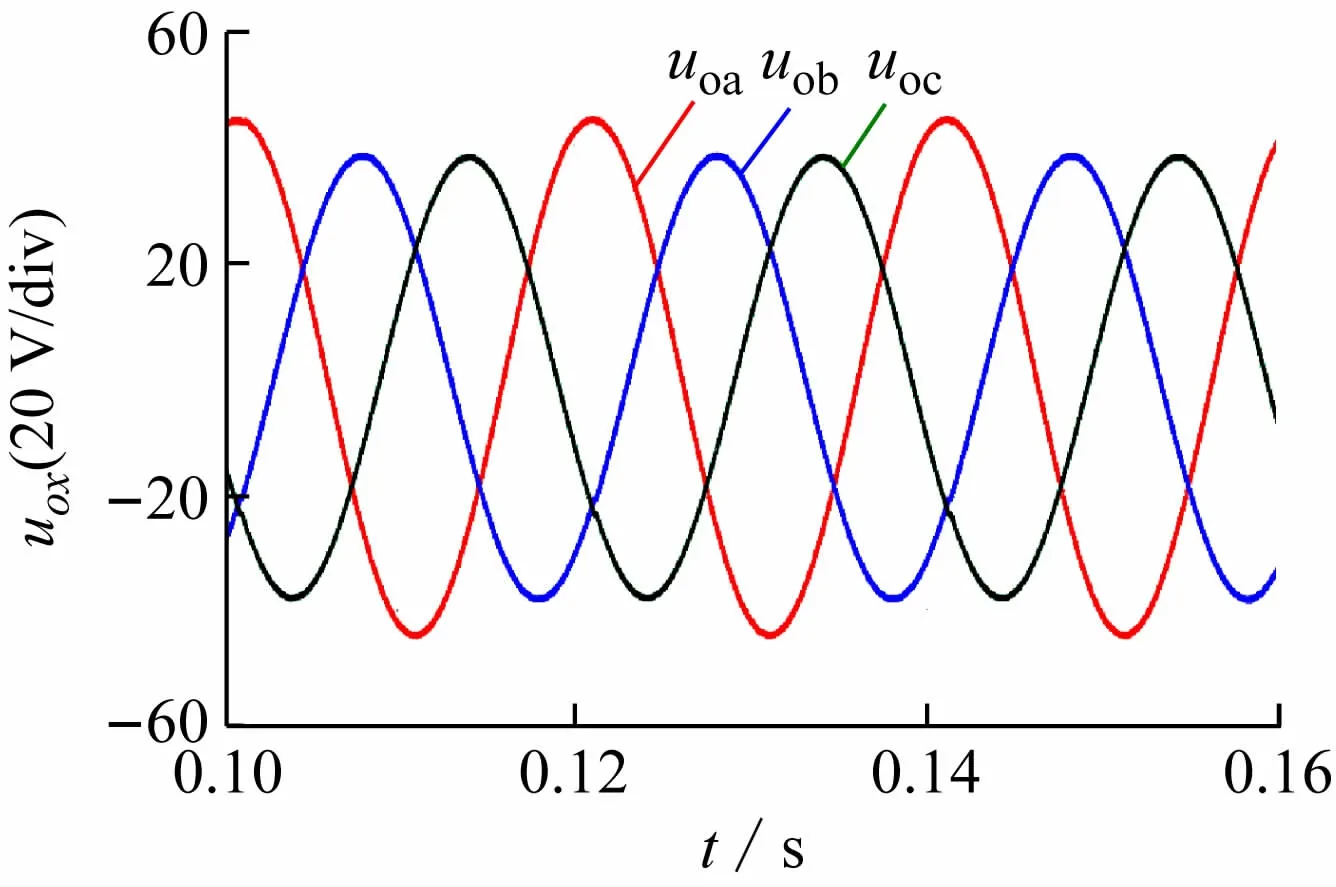
图10 逆变器输出电压
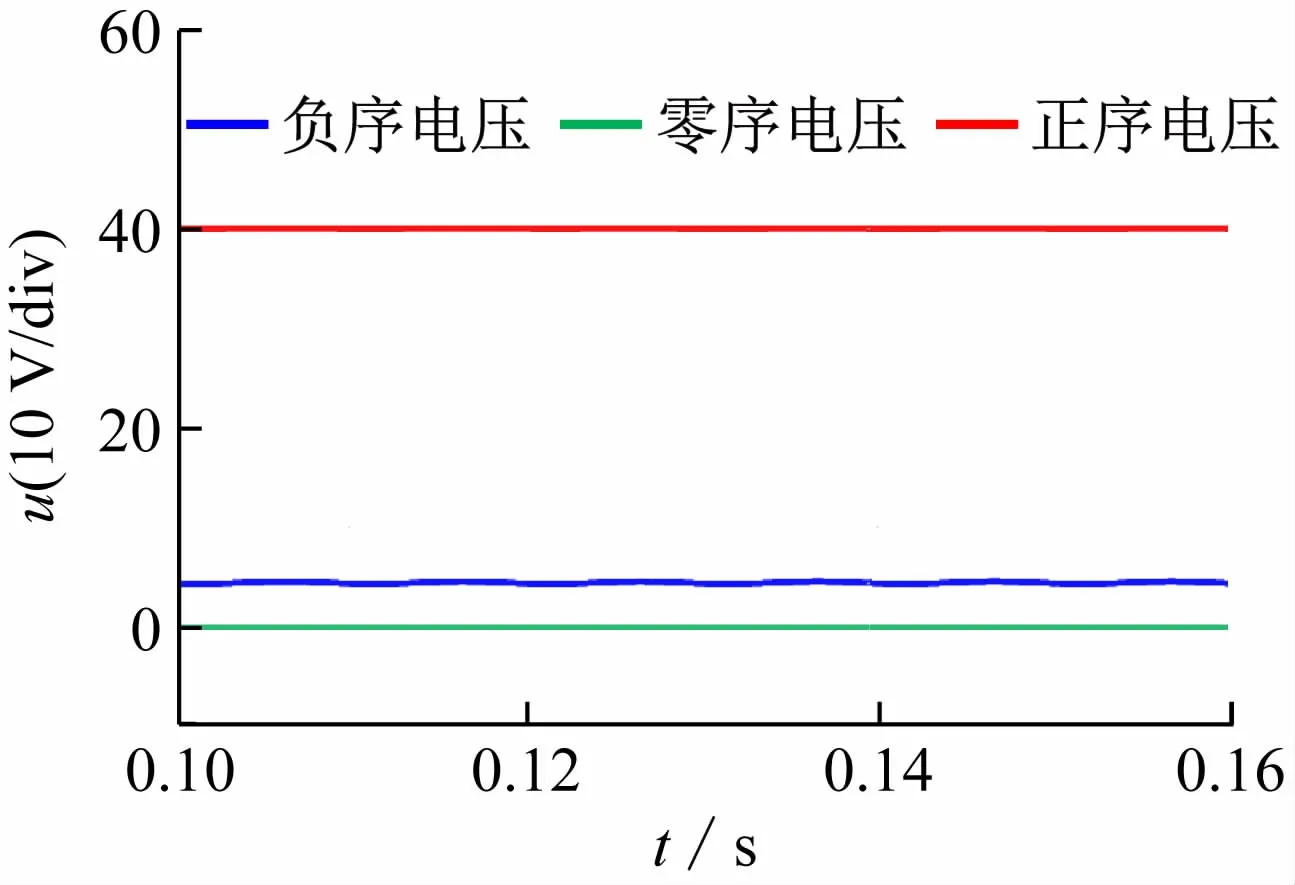
图11 正序、负序、零序电压幅值
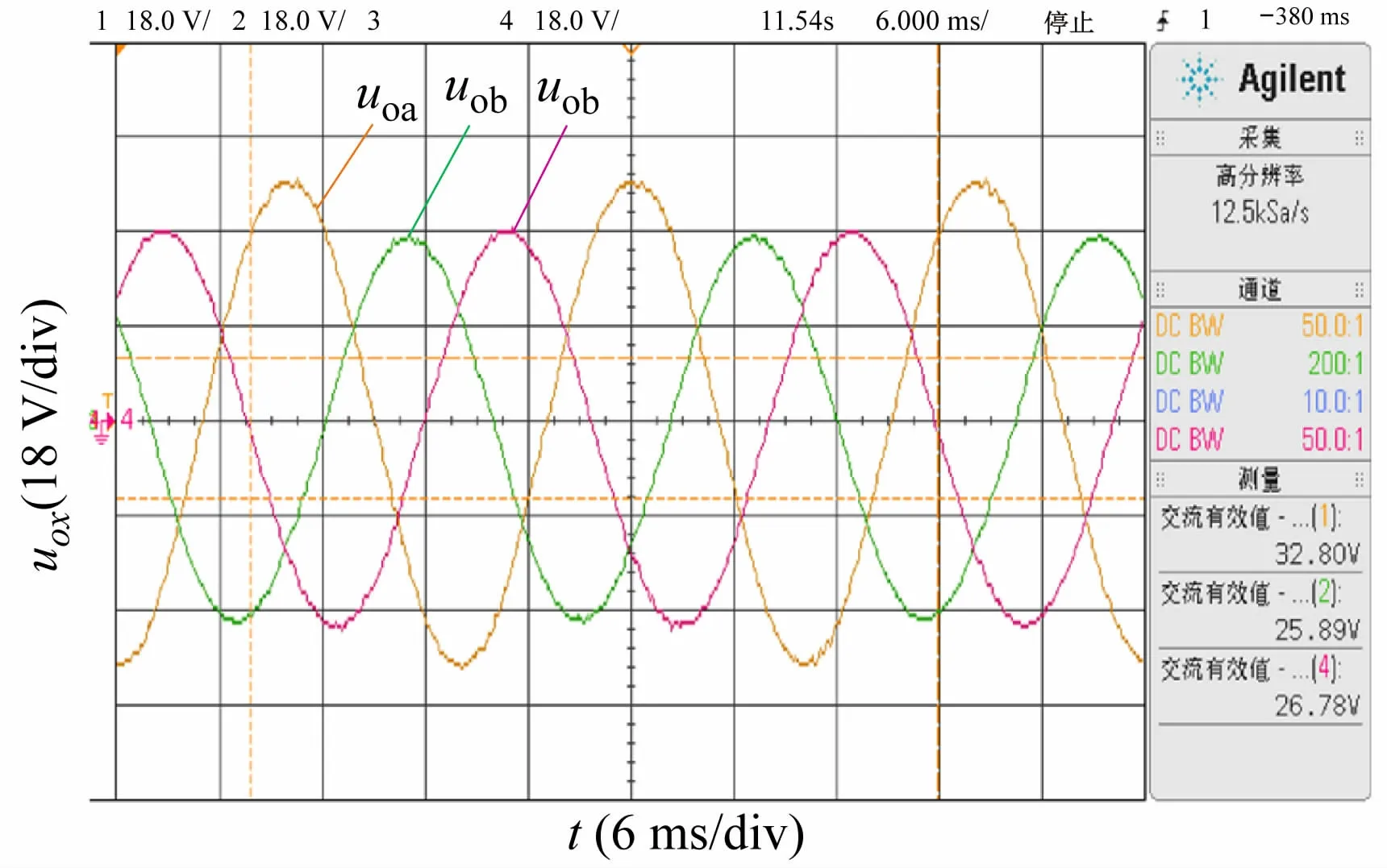
图12 逆变器采用前馈解耦控制且负载不平衡实验波形
当采用重复控制器后,仿真波形如图13、14 所示。由图可见,逆变器输出的三相电压依然对称,且正弦度很高,基波电压幅值为39.35 V,稳态误差很小,THD含量仅为0.54%。可见,当三相负载不平衡时,重复控制依然可以控制逆变器输出三相对称的电压。
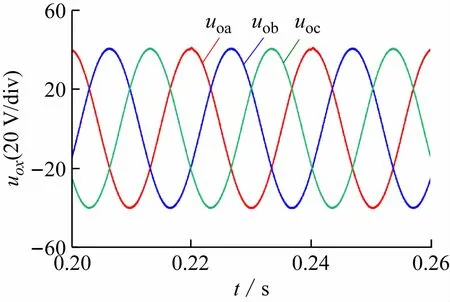
图13 逆变器输出电压
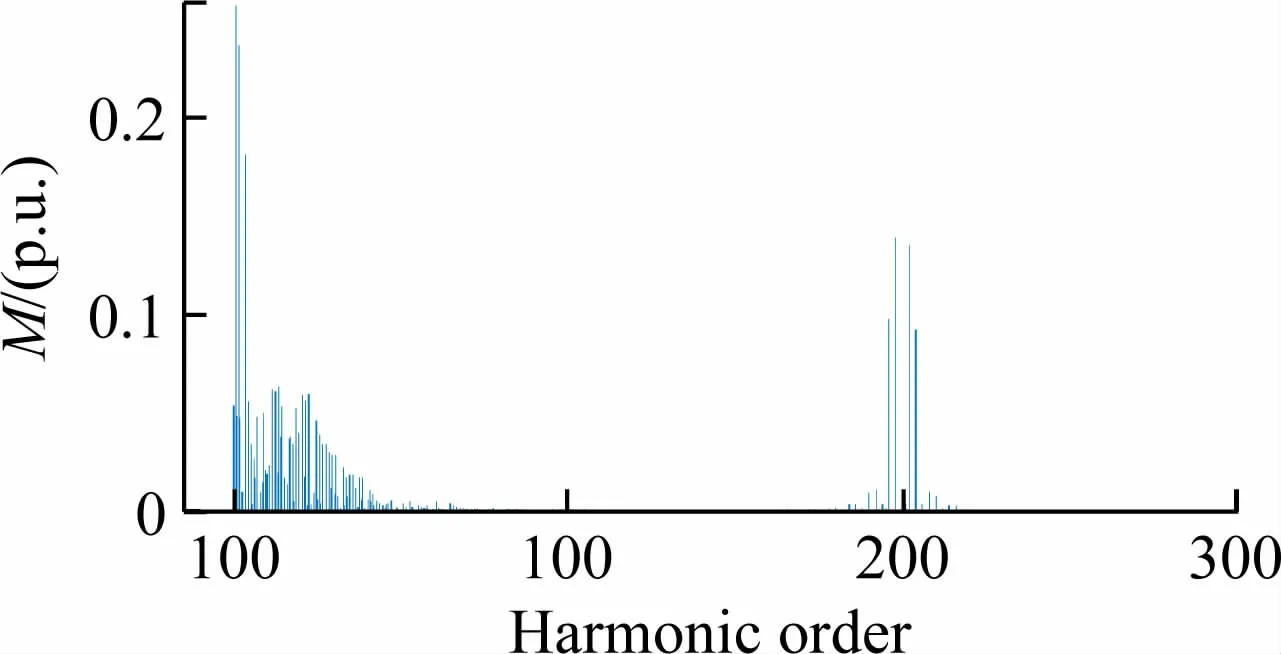
图14 A相电压FFT分析
三相负载不平衡时,A 相负载20 Ω、B 相与C 相均为负载10 Ω,逆变器采用重复控制器时实验波形如图15 所示。在稳态时,逆变器三相输出电压的有效值分别为:28.40、28.82 和28.05 V,三相电压更加对称。由图16 可见,基波电压幅值为39.72 V,THD 为1.97%。可见,采用重复控制器可抑制输出电压中的负序分量,减小三相电压不平衡。
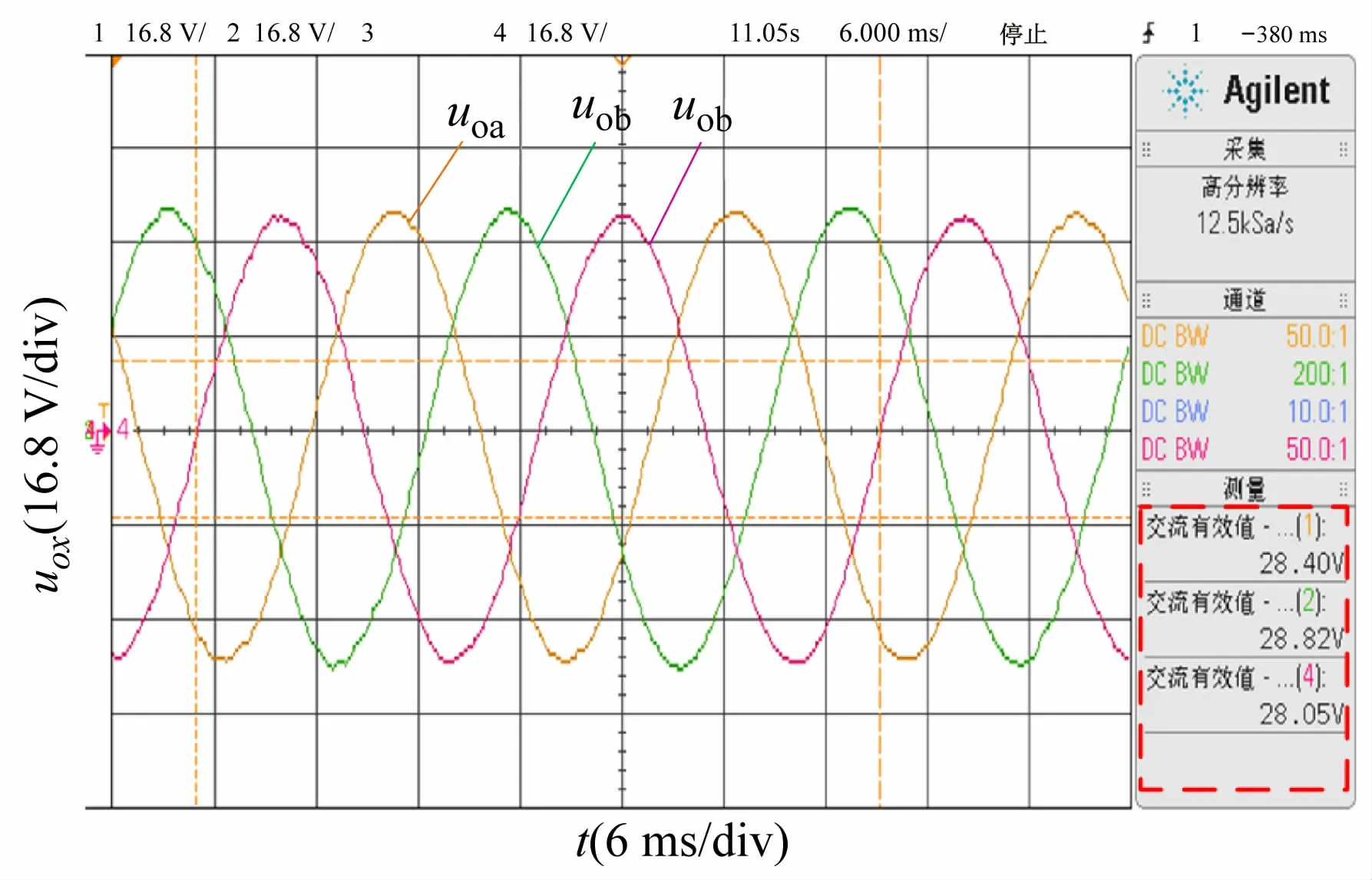
图15 逆变器采用重复控制且负载不平衡实验波形

图16 逆变器A相输出电压FFT分析
5 结 语
重复控制器结构简单,DSP计算负担小,稳态控制精度高,可抑制负序电压分量与谐波分量。本文对重复控制器的原理、结构、性能进行了详细分析,并完成重复控制器的设计与稳定性校验。“嵌入式”重复控制器在三相逆变器带不平衡负载时,逆变器输出电压对称,对其中的负序分量进行了抑制,减小了三相不平衡度。
