增强型中线划分色移键控码实验设计

李宗艳， 袁泽宇， 孙 政， 何淩燕， 李世银

（中国矿业大学信息与控制工程学院，江苏徐州 221116）

0 引 言

数字化时代，对适应数字化转型中高素质创新人才的迫切需求，成为高等教育必须回答的时代命题。引导学生了解科技前沿发展，开设创新实验教学，已成为提升学生科研素养和创新能力的一种有效途径［1-3］。同时，通过创新实验设计提高学生的工程实践能力［4］。可见光通信（Visible Light Communication，VLC）以可见光为载体进行信号传输，具有频谱无须授权、节能、高安全性等优势，已被IMT-2030（6G）推进组列为6G候选关键技术之一［5］。色移键控（Color-Shift Keying，CSK）是一种通过改变红／绿／蓝（R／G／B）LED光强度来传输数据的调制方案，对应恒定光强度约束以避免LED闪烁，满足人眼无法感知光闪烁特性［6］。文献［7-8］中分别使用台球法和内点法研究二维三角形平面中CSK星座设计。文献［9］中研究了一种增强型CSK星座设计方案。此外，还有学者还对二维三角形平面中的CSK 星座进行优化设计，以进一步提高VLC系统传输性能［10-12］。恒定光强度特性将CSK 星座限制在二维三角形平面，无法充分利用三色分量的三维光强度空间的自由度［13-14］。为提高VLC 系统性能，文献［15-16］中研究了感知色约束下的CSK 编码方案。

为进一步提高VLC系统的功率效率，增大可见光信号的传输距离，本文提出一种基于可见光通信的增强型中线划分色移键控（Median Partition Color-Shift Keying，MPCSK）码实验方案。基于感知色约束，提出一种增加星座点的三维光强度空间MPCSK 星座更新方案。基于MPCSK 星座与有限状态机（Finite State Machine，FSM）提出感知色约束的高编码增益MPCSKFSM编码方案。基于VLC 系统模型对提出的增强型MPCSK-FSM实验方案的误码率性能进行仿真。

1 系统描述

1.1 VLC系统模型

基于CSK-FSM的VLC系统一般模型，如图1所示。

图中，发送的二进制数据序列b被划分成mbit子序列，其中每个子序列bl＝（bl1，bl2，…，blm），且R＝（b1，b2，…，b2m）。其次，设定CSK 调制的符号集S ＝｛s1，s2，…，sM｝，其中符号向量si ＝［sr，i，sg，i，sb，i］T为光强度空间第i个星座点。因而，基于常规CSK 调制的VLC系统，子序列bl与符号向量si之间一对一映射关系χ可描述为

对CSK-FSM 映射方案的VLC 系统，需要依据给出的FSM编码结构确定发送子序列bl与符号向量si之间的映射关系。符号si经数模转换（Digital-to-Analog Converter，D／AC）后，使用强度分别为sr，i、sg，i和sb，i的R／G／B三色LED发射光信号至VLC信道。

接收端，分别使用R／G／B三色光学滤波器输出三色光信号并经光电检测器（Photodetectors，PD）得到接收信号

式中：H为信道增益矩阵；n 为均值为0、方差为σ2的高斯白噪声。ri经模数转换（Analog-to-Digital Converter，A／DC）输出至CSK-FSM 检测模块，最终输出估计数据序列b＾。

1.2 MPCSK星座

（1）常强度三角形平面MPCSK 星座。基于常规白光照明的室内场景，CSK调制的VLC 系统需满足目标感知色-白光约束。因而，文献［16］中常强度三角形平面的MPCSK 星座是一种可行方案，其主要是在强度平面三角形的中线上进行对称性星座点设计，所得MPCSK星座点的个数M＝3K，K＝2，3，6，如图2 所示，图中Tc为感知色约束。

图2 常强度三角形平面MPCSK星座

（2）多强度三角形平面MPCSK 星座。多强度三角形形平面M-MPCSK（M＝6，9）星座，如图3 所示。

图3 多强度三角形平面MPCSK星座

基于感知色约束，考虑以星座点至Tc的欧式距离相同的对称性符号为划分准则，对星座符号集划分成α（α ＝1，2）个符号子集；将不同符号子集映射至不同的光强度平面Lα。符号子集映射准则：从提高功率效率角度，将星座结构中MED大的符号子集映射至低强度平面；反之，MED小的符号子集映射至高强度平面；同时，考虑不同强度平面的星座点之间的MED 相等。由上述星座符号子集划分准则和符号子集映射准则可知，多强度平面18-MPCSK 星座可由4 个强度三角形平面组成。

1.3 有限状态机

由文献［15］中可知，CSK 编码结果可使用由状态、边和标签描述的FSM 来构造。基于数学理论，FSM可以用邻接矩阵D 表示，其对应元素Dij＝0 和Dij＝1 分别为从当前状态STi到下一状态STj有转移和无转移。文献［17］中将FSM容量定义为

式中，λmax为行列式方程的最大实根，其单位为bit／符号，I是单位阵。

2 增强型MPCSK-FSM码设计

为进一步提高MPCSK 码的传输性能，提出一种Q＝4 状态增强型MPCSK-FSM 编码方案。为满足状态数Q＝M-2m＋1 约束，m＝ lbM，需对三维信号空间中M-MPCSK 星座进行更新，M∈｛6，9，18｝。从提高功率效率角度，同时考虑感知色约束，本文通过在三维强度空间的中心线增加符号坐标实现对星座更新，得到更新的M-MPCSK 星座点s′i，使其满足Q＝M-2m＋1 约束，如图4 所示，M∈｛7，11，19｝。

图4 更新M-MPCSK星座，M∈｛7，11，19｝

本文提出的增强型MPCSK-FSM编码方案，主要包含2 级符号子集划分和FSM构建2 个步骤。

步骤1 两级划分符号子集

依据图4 所示的星座结构，对MPCSK星座符号集进行Q＝4 个符号子集S（α1）的划分，且满足｝。本文考虑基于最小化平均光强度功率PM和感知色约束，进行第1 级符号子集划分准则设计

式中，κ为正实数。因此，基于第1 级符号子集划分准则，很容易得到7-MPCSK、11-MPCSK 及19-MPCSK 星座的可能符号子集S（α1）（见表1）。

表1 M-MPCSK星座的符号子集

基于图4 星座和表1 中符号子集S（α1），设计第2级符号子集划分准则。本文考虑两种情况

式中，Lsi（Lsj）为符号si（sj）所在三角形平面的光强度值。针对最大强度平面中星座点个数大于3 的情况，选取满足白光约束的星座点为一个符号子集，其他星座点为另外一符号子集。基于第2 级符号子集划分准则，很容易得到划分后的符号子集S（α1，α2）（见表1）。

步骤2 构建状态数Q＝4 的FSM

基于符号子集S（α1，α2），所构建的MPCSK-FSM码对应4 个状态分别为ST1、ST2、ST3和ST4。首先，以FSM中当前状态ST1的转移结构为例，其对应下一个候选状态可以是ST1、ST2、ST3和ST4。分别使用S（1，1）、S（1，2）、S（1，3）和S（1，4）表示从ST1转移至ST1、ST2、ST3和ST4的输出符号子集；具体来讲，为使MPCSK-FSM码满S（1，3）和S（1，4）应分别对应4 条不同状态转移路径上的输出符号子集。同理，该方法同样用于当前状态为ST2、ST3和ST4的情况。最终，本文所构建的MMPCSK-FSM码的FSM 结构如图5 所示，M∈｛7，11，19｝。

图5 4状态M-MPCSK-FSM码的FSM，M∈｛7，11，19｝

为求解MPCSK 星座中各符号坐标，提出一种基于特定α1值下任意2 个符号子集S（α1，α2）之间MED相等的临界值方法；同时，本文考虑一个约束条件

式中，dpat为2 个不同MPCSK 符号转换路径的MED。依据式（5）、（6）给出的约束条件，同时设置图4 所示对称星座结构中多个强度面中的一个三角形平面光强度为常数，这样很容易写出星座坐标的线性方程。对线性方程使用高斯消元法可求解出符号坐标。最终M-MPCSK星座（见表2）。

表2 M-MPCSK星座点

此外，对FSM结构分析得知，其存在多种可能情况，基于式（5）、（6）约束，MPCSK-FSM 码的MED，dc，min，不变，这是因为dc，min＝min｛d2par，d2pat｝。因而，为不失一般性，可以选取一种可能MPCSK-FSM 码的FSM结构（见图5）。

3 仿真分析

本小节给出了所提4 状态MPCSK-FSM码误码率（Bit Error Rate，BER）性能的仿真结果。仿真过程中，使用Viterbi 译码算法对MPCSK-FSM 码和对比CSK码进行解码，而未编码的各种CSK调制使用最大似然准则进行检测解调。

表3 ～5 分别列出了MPCSK-FSM 码信息数据与输出符号之间的映射关系。

表3 7-MPCSK-FSM码数据信息与输出符号之间映射关系

表4 11-MPCSK-FSM码数据信息与输出符号之间映射关系

表5 19-MPCSK-FSM码数据信息与输出符号之间映射关系

3.1 仿真分析

表6 中列出了基于多强度面星座的4 状态MPCSK-FSM码对应不同数据速率R下归一化平方最小距取值。

表6 各种方案的n

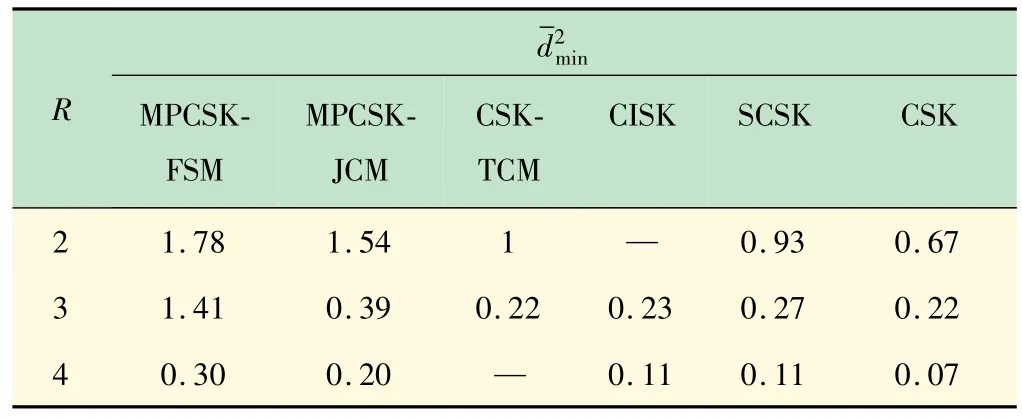
表6 各种方案的n

d2 min R MPCSKFSM MPCSKJCM CSKTCM CISK SCSK CSK 2 1.78 1.54 1—0.93 0.67 3 1.41 0.39 0.22 0.23 0.27 0.22 4 0.30 0.20—0.11 0.11 0.07

图6 各种方案归一化最小距离与数据速率

3.2 仿真结果

基于图1 所示的VLC系统模型，对各种CSK码和未编码CSK方案在信噪比（SNR）下的BER性能进行了仿真，如图7 所示。

图7 不同R、Q、M-MPCSK-FSM方案的BER对比

从图7 中可以得出如下结论：

（1）在数据速率R＝2 bit／符号且BER 为10-5时，如图7（a）所示，状态数Q＝4 的7-MPCSK-FSM 码相比于其他方案具有最优BER 性能；具体来讲，与状态数Q＝3 的6-MPCSK-JCM码相比，其具有约1.8 dB的编码增益；相比于4-CSK、6-CSK-TCM和4-SCSK，分别实现了大约4.1、3.2 和2.6 dB的编码增益。

（2）在数据速率R＝3 bit／符号且BER 为10-5时，如图7（b）所示，Q＝3 和Q＝4 的两种码的BER性能明显优于其他对比方案，其中后者与前者相比具有约2.6 dB的编码增益；此外，与8-CSK、（4，2）-CISK、10-CSK-TCM 和8-SCSK 相比，4 状态增强型MPCSKFSM码，分别实现了大约5.6、4.9、4.8 和4.4 dB的编码增益。

（3）在数据速率R＝4 bit／符号且BER 为10-5时，如图7（c）所示，状态数Q＝4 的19-MPCSK-FSM码相比于状态数Q＝3 的18-MPCSK-JCM 码具有约1.2 dB 的编码增益；相比于16-CSK、（8，2）-CISK 和16-SCSK 4 状态增强型MPCSK-FSM 码，分别实现了大约5.0、2.8 和2.8 dB的编码增益。

由图7 可见，本文所提增强型4 状态MPCSK-FSM码具有明显的BER 性能优势。通过对维特比解码算法的分析可知，基于一定数据速率R下所提方案的复杂度与状态数Q之间的关系为Ο（Q）。因而，增强型MPCSK-FSM码的实现复杂度是未编码CSK 码的Q＝4 倍。

4 结 语

为提高CSK 码的功率效率，提出了一种增强型MPCKS-FSM码的设计方案。基于感知色约束，通过设计两级符号子集的划分准则与增加编码结构的状态数，构建4 状态的FSM 编码结构来获取高编码增益。同时，本文通过引入最小平方欧式距离对提出的4 状态MPCSK-FSM编码方案与对比方案进行了对比分析。此外，基于VLC系统进一步对增强型设计方案进行了BER性能的仿真验证。实验结果表明，与现在的实验方案相比，所提出的4 状态MPCSK-FSM 码具有最优的功率效率。