合作型协同进化遗传算法求解分布式柔性作业车间调度问题*
2023-12-11董博文王有远
董博文 王有远
(①南昌航空大学飞行器工程学院,江西 南昌 330063;②南昌航空大学工业工程研究所,江西 南昌 330063;③南昌市航空复杂系统与智能科学重点实验室,江西 南昌 330063)
随着经济全球化发展,许多制造企业由集中式制造向分布式制造转变,生产制造不再局限于在单一工厂进行,而是多工厂协同制造。生产调度在分布式制造中进一步延伸,在机械加工等制造场景中,产生了分布式柔性作业车间调度问题(distributed flexible job shop scheduling problem,DFJSP)。DFJSP属于NP(难问题),对其进行优化有助于缩短制造期、提高机器利用率,因此其研究具有重要的学术意义和应用价值。
国内外学者对DFJSP 进行了相关研究。Chan F T S 等[1]最早研究了DFJSP,提出了一种基于支配基因的遗传算法,对问题解空间进行了完全编码;Giovanni L D 等[2]使用不完全编码方式,只编码了工厂分配和工序排序信息,通过解码确定机器选择,提出一种改进遗传算法(IGA)求解DFJSP;Lu P H 等[3]和Wu M C 等[4]分别使用工件序列(GA_JS)和工序序列(GA_OP)一维编码,设计启发式规则进行解码;Marzouki B 等[5-6]使用分散禁忌搜索(DTSMA)和化学反应优化算法(CRO)求解DFJSP;吴锐等[7]提出一种改进人工蜂群算法,引入基于关键路径的局部搜索算子提高算法局部搜索能力;吴秀丽等[8]设计了一种改进差分进化算法(IDESAA),利用模拟退火提高算法的局部搜索能力;孟磊磊等[9]提出了一种混合蛙跳算法(HSFLA),结合变邻域搜索提高算法的局部搜索能力;Li X Y 等[10]使用工厂分配和工序排序双层编码,提出一种改进灰狼优化算法(IGWO),使用基于关键工厂和关键路径的邻域搜索策略。
上述研究主要通过在部分解空间搜索来降低对DFJSP 的求解难度,随着问题规模增大解空间急剧扩大,算法全局搜索能力不足,寻优能力变差。本文提出一种合作型协同进化遗传算法(cooperative co-evolutionary genetic algorithm,CCGA)求 解DFJSP,利用分而治之的思想将问题分解为多个低维子问题,使用随机协同机制促进子种群协同进化以提高算法全局搜索能力。为弥补协同进化全局搜索能力强而局部开发能力弱的缺点,使用基于关键工厂的多重局部扰动策略,提高算法的局部开发能力。通过对公共基准算例进行测试并与其他算法对比,验证了所提算法的有效性。
1 分布式柔性作业车间调度问题
DFJSP 描述如下:给定n个待加工工件J={J1,J2,···,Ji,···,Jn},需要将其分配给q个工厂U={U1,U2,···,Ul,···,Uq}加工。工件i有ni个工序Ji={Oi1,Oi2,···,Oij,···,Oini},若工件i分配到工厂l加工,则该工件所有工序均在该工厂内加工。工厂l有ml台机器 Ml={Ml1,Ml2,···,Mlk,···,Mlml},可加工工序Oij的机器集合为每台机器在同一时刻最多只能加工一个工序,任一工件在任一时刻只能在一台机器上加工。工序一旦开始加工便不能中断,同一工件的所有工序需满足优先约束。所有工厂、机器和工件都在0 时刻可用,加工时间在不同工厂以及机器上可能不同。DFJSP 的目标是将工件分配给工厂、选择加工工序的机器和确定各机器上的加工顺序,使得调度的最大完工时间最短。DFJSP 的数学模型可参考Meng L 等[11]归纳的4 种主要模型。
2 合作型协同进化遗传算法求解DFJSP
2.1 编码与解码
为使算法在解空间的较优区域搜索,采用工厂分配和工序排序解耦编码方式,在解码时基于机器负荷确定机器选择。一个DFJSP 实例见表1,表中“-”表示该工序无法在该机器加工。该实例的一个编码方案如图1 所示,工厂分配编码FA 长度与工件数相同,第i个基因表示工件i所分配的工厂,如第1 个基因表示工件J1分配到工厂2。工序排序编码OS 长度与总工序数相同,使用工件号编码,工件号出现的次数表示第几个工序,如第4 个基因为3,第二次出现,表示为工序O32。

图1 DFJSP 实例的一个编码方案

表1 DFJSP 实例
染色体解码依OS 顺序依次解码,根据FA 编码确定工序所在工厂,进而确定可用机器集。选择最大完工时间最小的机器,当具有相同的最大完工时间时,选择加工时间短的机器,若加工时间也相同,则随机选择。在将工序分配给机器时,使用贪心策略,将工序安排在尽可能早地符合要求的机器空闲中,使得完工时间最小。图1 所示的第一个基因表示工序O21,根据FA 可知工件J2分配到工厂1,对应有两台机器M11和M12可加工,工时分别为1和2,显然在机器M11上的完工时间比在M12上短,因此选择机器M11加工工序O21。图1 编码方案对应的调度甘特图如图2 所示。

图2 编码方案对应的调度甘特图
2.2 协同机制
CCGA 的思想是将问题分解为多个子问题,分而治之。子问题之间的协同机制是CCGA 的一个关键因素,子种群中个体的适应度评估需要与其他子种群中的个体协作。常见的协同机制包括最优个体协同选择、最差个体协同选择、随机个体协同选择等。为提高算法全局搜索能力,使用随机个体协同机制,以尽可能多地搜索解空间。对于工厂分配子种群中的一个个体Pi,随机选择工序排序子种群中的一个个体,组合成完整染色体,通过解码得到的最大完工时间即为Pi的适应度,工序排序子种群中的个体适应度评估类似。
2.3 种群初始化与进化算子
初始种群的质量对于算法迭代搜索有一定的影响,好的初始种群能够帮助算法找到更优解。为提高初始种群质量,随机生成OS 部分编码,使用Lu P H 等[3]提出的基于工厂负荷的工厂分配方法确定FA 部分编码。
选择算子用于模拟适者生存的原则,能够帮助种群向最优个体收敛,使用三元锦标赛进行选择,以平衡随机协同机制收敛速度慢的影响。
交叉有助于增加种群多样性,工厂分配编码使用单点交叉,工序排序编码使用两点顺序交叉[4],如图3 所示。两个交叉点将个体分为3 段,子代C1保留父代P1的第一段和第三段,在父代P2中删除这些基因,剩余部分即为C1第二段。这样能保证得到的子代依然是可行解,且最大限度继承父代的编码信息。子代C2使用类似的方法产生。

图3 工序排序两点顺序交叉
变异能在一定程度上避免算法陷入局部最优解,使用逆转变异算子对FA 与OS 进行变异,即任意选取两点,逆转两点之间的基因顺序。
2.4 多重局部扰动策略
DFJSP 中完工时间最大的工厂称为关键工厂,关键工厂中具备最大完工时间的路径称为关键路径,关键路径上的工序称为关键工序。只有关键工厂和关键路径发生变化,才可能打破原有调度得到更优解。CCGA 将问题分解为多个子问题,分而治之,优势是能够更加充分搜索解空间,缺点是局部开发能力较差。为提高所提算法的局部开发能力,设计如下6 个邻域扰动算子。
邻域1:将关键工厂中的一个工件分配到完工时间最小的工厂中。
邻域2:将关键工厂的工序分成k段,每一段第一个基因与其他基因交换。
邻域3:将关键工厂的工序分成k段,重排k段的顺序。
邻域4:随机选择一个关键工序,与关键工厂的其他工序交换。
邻域5:随机选择一个关键工序,插入到关键工厂工序序列的某个位置。
邻域6:对于关键工厂中关键路径,采用移动一个工序的邻域搜索方法。
邻域2 和3 改编自Zhu J 等[12]提出的部分成对交换和简单插入,将均匀分为k段改为随机点位分段。邻域4 和5 改编自Valente J M S 等[13]提出的邻近非邻近交换和插入,将随机选择一个工序改为选择一个关键工序。邻域6 为Mastrolilli M 等[14]针对FJSP 提出的移动一个关键工序邻域结构。
多重局部扰动过程如下:
Step1:随机选择一个邻域扰动算子。
Step2:根据邻域结构生成一个新解。
Step3:若新解优于原解,以新解为中心返回Step1,否则返回Step2,直到邻域结构全部搜索完。
为提高计算效率,设定只有当新个体适应度不超过最优解d时才进行多重局部扰动,同时为避免进化后期种群收敛造成大量个体满足上述要求导致计算量增大,设定每个种群最多15%的个体能够进行多重局部扰动,且增加选择概率,rand< 0.5时才进行多重局部扰动,提高局部搜索的均匀性。
2.5 算法整体框架
CCGA 算法伪代码如算法1(图4),4~10 行表示工厂分配子种群和工序排序子种群分别进化;11~23 行表示使用随机协同策略评估个体适应度,并对满足条件的个体进行多重局部扰动;26~28 行表示在算法陷入局部最优时引入随机个体,提高种群多样性继续搜索,以帮助算法跳出局部最优。

图4 CCGA 算法伪代码
3 实验验证
采用De Giovanni L 和Pezzella F[2]基 于23 个FJSP 基 准(la01-la20、mt06、mt10 和mt20)拓 展到2/3/4 工厂情形下生成的69 个DFJSP 基准验证CCGA 的有效性。使用Matlab R2020b 编程,取种群规模N=200、最大迭代次数G=150、交叉概率Pc=0.95、变异概率Pm=0.01、局部扰动比例参数d=0.2,每个基准独立运行30 次。
3.1 多重局部扰动策略有效性验证
为验证多重局部扰动策略的有效性,使用2 工厂下的23 个基准进行对比实验,对比结果见表2。
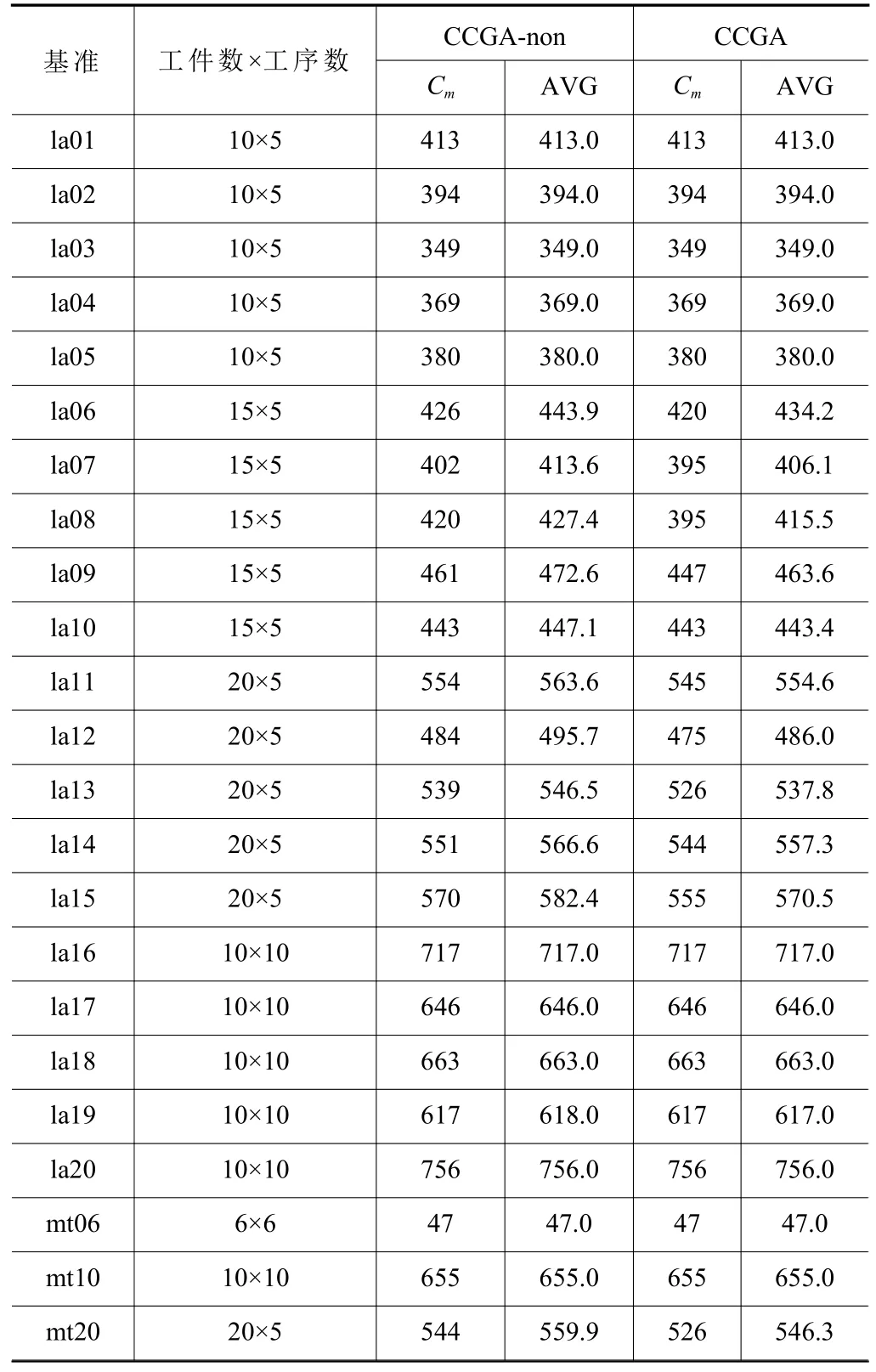
表2 CCGA-non 与CCGA 对比实验
表2 中CCGA 表示带多重局部扰动策略,CCGAnon 表示不带多重局部扰动策略,Cm表示所求得的最好的最大完工时间,AVG 表示平均最大完工时间。23 个基准中有10 个基准(la06-la09、la11-la15、mt20)CCGA 求得的最优解和平均值都比CCGAnon 好,剩余13 个基准所求得的最优解相同,其中CCGA 在基准la10 和la19 上的平均值比CCGAnon 好。使用Minitab 19.1 对两个算法在23 个基准上求得的最优值和平均值进行Wilcoxon 符号秩检验,置信区间为95%,得到p值为0.006 和0.003,均小于0.05,说明CCGA 在统计意义上显著优于CCGA-non,即多重局部扰动策略是有效的。
3.2 CCGA 算法有效性验证
将CCGA 与其他求解DFJSP 的算法进行比较,所求得的最优解对比结果见表3 和表4,表中最后一行为使用Wilcoxon 符号秩检验得到p值,最后一列带“*”号表示CCGA 找到基准下界。在2 工厂情形时,所有算法在la01~la05、la16~la20、mt06以及mt10 基准上均能找到下界。剩余11 个基准中,CCGA 求得的最优解均优于IGA、DTSMA、CRO和GA_JS,且Wilcoxon 符号秩检验得到p值均小于0.05,证明CCGA 优于IGA、DTSMA、CRO 和GA_JS 这4 个算法。对于GA_OP 和IDESAA,CCGA分别在3 个和4 个基准上找到更优,Wilcoxon 符号秩检验得到p值均大于0.05,说明GA_OP 和IDESAA在统计意义上与CCGA 无显著差异。对于IGWO和HSFLA,求解结果和p值均表明其优于CCGA。
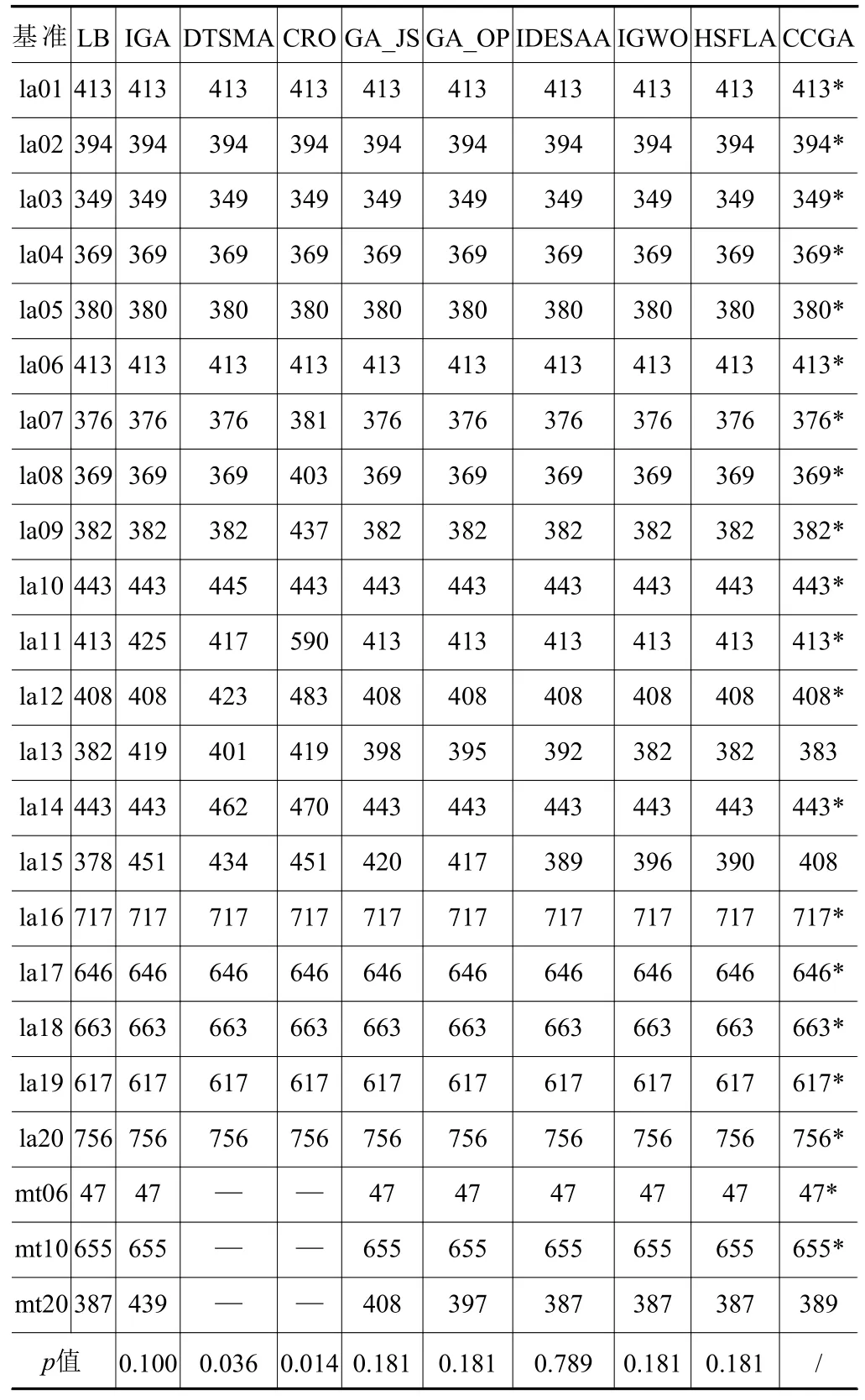
表4 CCGA 和其他算法计算结果对比(3 工厂)
在3 工厂实验中,由于生产资源增加,但是生产任务没有变化,因此比较容易找到最优解。从表4 可以看出,CCGA 在3 工厂情形下求解结果比IGA、DTSMA、CRO、GA_JS 和GA_OP 要好。与剩余算法求解结果主要在基准la13、la15 和mt20上不同,Wilcoxon 符号秩检验p值均大于0.05,表明CCGA 与这些算法在统计意义上没有显著差异。
4 工厂情形时可用生产资源进一步增加,CCGA和GA_JS、GA_OP、IDESAA、IGWO、HSFLA 均能找到23 个基准的最优解,在此不再列出实验结果。从以上结果分析可知,CCGA 在求解DFJSP 时是有效的。图5 所示为2 工厂情形时基准la08 的最优调度甘特图。

图5 2 工厂情形la08 基准调度甘特图
4 结语
本文提出了一种合作型协同进化遗传算法求解DFJSP,利用分而治之的思想提高全局搜索能力,并设计多重局部扰动策略提高算法的局部开发能力。在公共基准上的实验结果以及Wilcoxon 符号秩检验表明多重局部扰动策略的有效性。在与其他算法对比中,所提算法优于IGA、DTSMA、CRO 和GA_JS这4 个算法,与GA_OP 和IDESAA 性能相近,略差于IGWO 和HSFLA,表明所提算法求解DFJSP 是有效的。
DFJSP 这类问题通常包含多个子问题,与合作型协同进化算法的分而治之思想相贴合,因此具有一定的研究潜力。未来可以使用不同的协同机制,或在求解子问题时使用不同的进化算法来设计合作型协同进化算法。也可以尝试使用合作型协同进化算法求解多目标DFJSP 以及其他车间调度问题。
