基于SGMD-CMAE 和WOA-ELM 的滚动轴承故障诊断方法*
2023-12-11吴仕虎杨鑫杰
吴仕虎 李 颖 杨鑫杰 巴 鹏
(沈阳理工大学机械工程学院,辽宁 沈阳 110159)
在运行过程中,滚动轴承极易发生故障,约40%的旋转机械故障是由滚动轴承引起的[1]。因此,实现滚动轴承故障的准确诊断,对旋转机械安全稳定地运行起重要作用。
对滚动轴承故障实现诊断,可以通过分析滚动轴承的故障振动信号来提取故障特征。但由于其信号具有非平稳性和非周期性的特点,且信号中含有大量噪声,导致故障特征提取存在困难[2]。因此,需要选择一种抗噪性能好的方法对信号进行处理。对此,国内外专家学者做了大量的研究。Huang N E 等[3]提出经验模态分解(empirical mode decomposition,EMD)方法,将复杂信号分解为多个信号分量。但在分解过程中,会产生模态混叠现象,导致分解结果产生错误[4]。变分模态分解(variable modal decomposition,VMD)解决了EMD 方法存在的模态混淆问题。刘备等[5]将VMD 方法应用到滚动轴承故障信号的预处理中,并取得了良好的效果。但VMD 方法需要人为设定模态个数,缺乏自适应性。潘海洋等[6]提出了辛几何模态分解,通过矩阵变换分解从而重构故障信号,并在行星齿轮箱信号故障中得到了应用[7]。SGMD 方法克服了模态混叠现象,自主确定有关参数,且具有良好的抗噪性。基于上述分析,选择SGMD 方法对滚动轴承故障信号进行处理。
提取故障信号特征是故障诊断关键一步。熵方法在故障特征提取领域有着广泛的应用[8]。雷春丽等[9]通过样本熵提取了轴承早期微弱故障特征,但样本熵(sample entropy,SE)存在特征提取过慢的问题。与样本熵相比,排列熵(permutation entropy,PE)提取速度有了明显的提升。毛欢等[10]利用排列熵提取了低速重载工况下的滚动轴承故障特征。但排列熵忽略了时序信号振幅的差异性,使得特征提取不全面。李可等[11]利用模糊熵(fuzzy entropy,FE)原理成功提取了滚动轴承故障信息,而模糊熵在故障特征提取过程中存在敏感度较低的问题,使得故障特征不能被充分的提取。为了克服上述熵的不足,Yang J W 等[12]提出注意熵(attention entropy,AE),AE 注重信号峰值点间隔的频率分布,所以AE 具有参数少、提取特征速度快和抗干扰能力强等优点。针对注意熵无法多尺度提取信号特征的问题,提出多尺度注意熵(multi-scale attention entropy,MAE)。基于多尺度熵粗粒化不足的问题,提出了复合多尺度注意熵。CMAE 能有效处理因粗粒化不足而产生的MAE 熵值波动问题,提升故障诊断模型的稳定性和准确性。
滚动轴承故障诊断的实质是滚动轴承故障类型的识别并分类。常见的分类模型有随机森林(random forest,RF)和极限学习机等。王兰兰等[13]在不同的工况条件下,通过随机森林模型识别出滚动轴承故障;但随机森林模型会在回归问题上出现过拟合。刘云斌等[14]将滚动轴承的精细复合多尺度离散熵特征输入到ELM 模型,实现了滚动轴承的故障诊断,但ELM 模型中输入层节点权值和隐藏层节点阈值两参数是随机生成,其泛化性不足。而鲸鱼优化算法具有优化参数效果好的优点。选用WOA 方法优化ELM 模型的输入层节点权值和隐藏层节点阈值,构建WOA-ELM 模型,以提高滚动轴承诊断故障模型的准确率。
综上所述,提出一种基于SGMD-CMAE 和WOAELM 的滚动轴承故障诊断方法。首先通过SGMD方法重构滚动轴承故障信号;再用CMAE 方法定量提取重构信号的特征,由此构建CMAE 特征;然后利用WOA 算法优化ELM 模型,构建WOAELM 模型;最后采用WOA-ELM 模型对CMAE 特征进行故障类型的识别并分类。
1 SGMD-CMAE 和WOA-ELM 故障诊断模型建立
1.1 辛几何模态分解
SGMD 是一种新的分解方法,通过将信号重构相空间,得到Hamilton 矩阵;再通过相似变换得到Hamilton 矩阵的特征向量,对特征向量进一步对角平均化处理重构辛几何分量,步骤如下。
第一步,构造矩阵。假设时序信号x=x1,x2,···,xn,用Takens 嵌入定理得:
式中:d为嵌入维数;τ为延迟时间;m=n-(d-1)τ。
第二步,辛几何矩阵变换。假设A=XTX,则Hamilton 矩阵:
令B=M2,矩阵B为Hamilton 矩阵,则辛正交矩阵S得:
式中:C为上三角矩阵,矩阵中元素cij=0(i>j+1)。通过矩阵计算求得矩阵C的特征值为λ1,λ2,···,λd。矩阵A的特征值为,与之对应的特征向量为Di(i=1,2,···,d)。重构的轨迹矩阵Z由各个单分量矩阵Zi(i=1,2,···,d)组成。
第三步,对角平均处理。对任意单分量矩阵Zi,zij(1≤i≤d,1≤j≤m)为矩阵Zi中元素。若m<d,则=zij,否则=zji。对角平均化公式为
式中:d*=min(m,d),m*=max(m,d)。
通过对角平均化公式,由一组Zi得到Yi=y1,y2,···,yn,从而求得初始信号的d组叠加成分,即d个辛几何模态分量。
第四步,信号筛选及重构。通过上述步骤,得到d个分量信号,但各分量之间不是完全独立的,可能具有相同的周期成分和故障特征。因此,选用周期相关性对各单分量信号进行筛选。相关系数表达式为
通过SGMD 方法对滚动轴承故障信号的重构,提高了重构信号的信噪比,为后续准确提取重构信号的特征奠定基础。
1.2 复合多尺度注意熵
1.2.1 注意熵
AE 是一种度量信号复杂性的工具,能有效提取故障信号特征。如图1 所示,AE 的具体计算步骤如下。
(1)将信号中的一个点看作一个小系统,则小系统之间的状态变化可以理解为整个信号系统的调整。局部峰值点的变化情况为整个系统波动情况,故将局部峰值点定为关键点。
(2)根据局部峰值点的{min-min}、{min-max}、{max-min}和{max-max}4 种方式设定为关键点,并计算间隔点数。
(3)计算关键点间隔香农熵,公式如下:
式中:p(x)表示x发生的概率;b表示间隔点种类个数。
(4)将4 种峰值点设定方式计算得到香农熵平均值定义为注意熵。公式如下:
1.2.2 复合多尺度注意熵
AE 以单一尺度计算时序信号熵值,难以准确地反映时序信号的有效信息。因此,将多尺度熵和注意熵相结合,形成了MAE 方法。MAE 方法粗粒化过程如图2 所示。在粗粒化过程中,粗粒化时序信号中3 的元素数量随尺度因子τ的增加而减小,这将导致MAE 熵值存在较大误差。为了提高MAE 熵值的准确性,改进的粗粒化过程如图3 所示。与传统的粗粒化过程相比,在尺度因子τ下,改进的粗粒化过程可以得到τ组时间序列,从而提升熵值的准确性。CMAE 方法计算步骤如下:
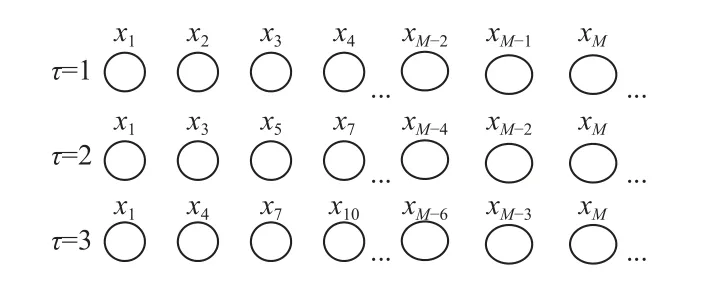
图2 传统粗粒化过程
(1)将长度为N的时序信号分为τ个子时序信号。
式中:x表示初始信号的样本点;τ表示尺度因子,k∈[1,N];表示在τ尺度下第β个子序列,β∈[1,τ]。
(2)计算同一尺度的子时序信号注意熵,将注意熵和的平均值定义为
(3)通过式(9)计算所有尺度因子τ的CAE(τ),并将这些CAE(τ)的集合定义为CMAE(τ)。
为验证CMAE 方法的合理性,处理了Red noise、Pink noise、Blue noise 和Violet noise 这4 种噪声信号。图4 所示为4 种噪声的时域图。

图4 噪音信号时域图
图5 所示为4 种噪声信号的MAE 和CMAE 值的分布情况。通过MAE 方法求取4 种噪声信号的MAE 值,发现4 种噪声信号的MAE 值均会发生波动,尤其以Blue noise 和Violet noise 的MAE 值变化幅度较大,分别为0.22 和0.34,说明传统粗粒化方法分割时序信号不够精准。CMAE 方法求取的4种噪声信号CMAE 值分别0.15、0.16、0.15 和0.24。与MAE 方法相比,CMAE 值变化幅度更小,总体更加平稳。同时,随着尺度因子τ的增加,CMAE值趋于稳定,说明CMAE 方法定量提取特征的稳定性更好。
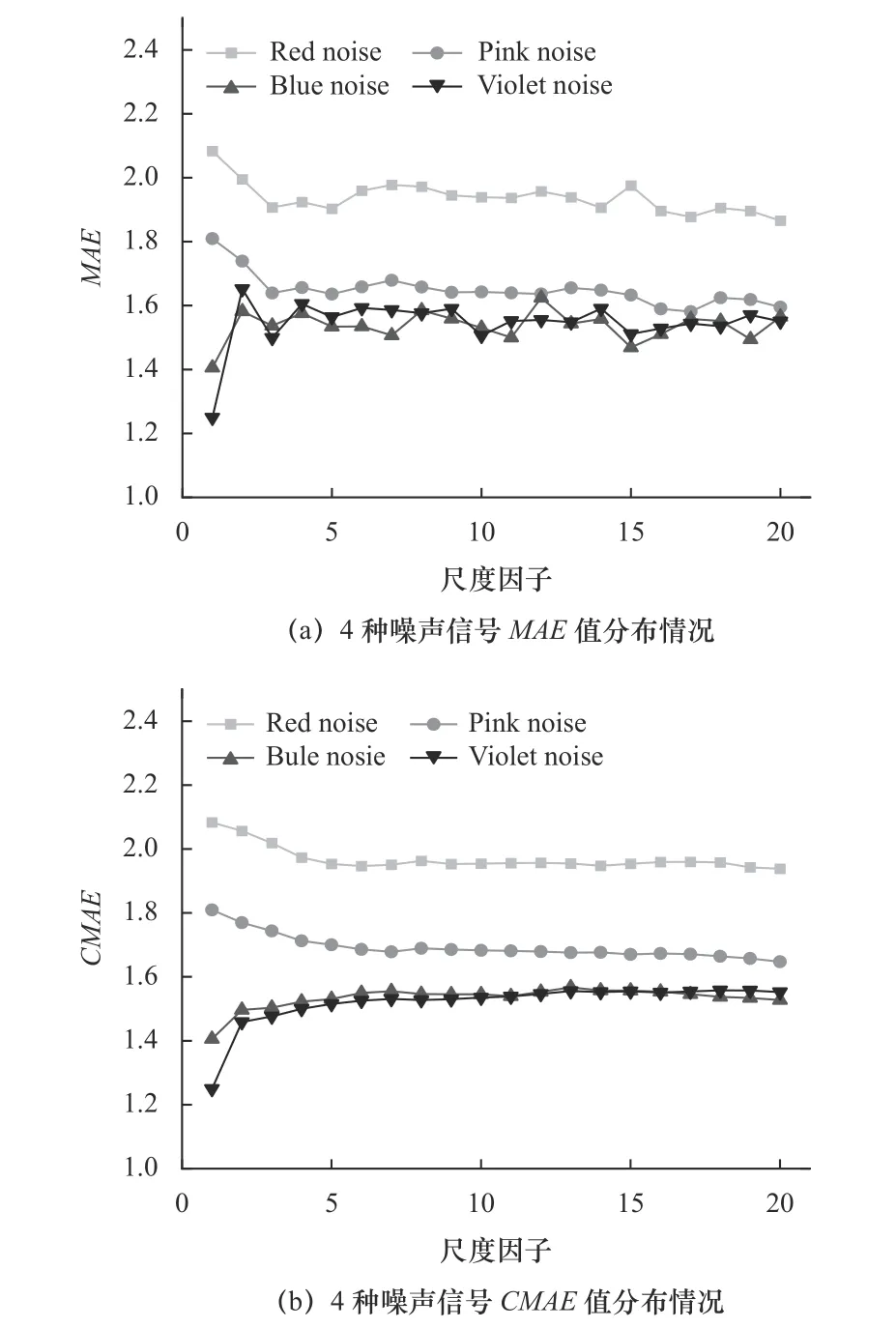
图5 MAE 和CMAE 分布情况
1.3 WOA-ELM 模型
1.3.1 极限学习机
ELM 是一种基于前馈神经网络模型。假设有Q个样本(xq,yq)(q=1,2,···,Q)。xq=[xq1,xq2,···,xqi]∈Ri;yq=[yq1,yq2,···,yqo]∈Ro。在ELM 模型中,输入层神经元为q,隐藏层神经元为l,输出层神经元为o,输入层节点权值为w,隐藏层节点阈值为h,隐藏层激活函数为g(x)=1/(1+e-x),并通过计算确定隐藏层节点权值β。模型如图6 所示。

图6 ELM 网络模型
模型的输出Y为
式中:wj=(w1j,w2j,···,wqj)T为第j个输入层节点权值向量;βj=(βj1,βj2,···,βjl)T为第j个隐藏层节点权值向量;hj为第j个隐藏层节点阈值。
1.3.2 鲸鱼优化算法(WOA)
鲸鱼优化算法是一种智能优化算法。其算法主要分为逐渐搜索[15]、螺旋搜索和随机搜索[16]3 种模式。
(1)逐渐搜索模型的表达式为
式中:t表示迭代次数;a和c表示系数;X(t)表示位置;X*(t)表示目前得到的最佳解的位置;X(t+1)表示下一次迭代后最佳解的位置;S表示当前搜索个体到猎物处的距离。
(2)螺旋搜索模型的表达式为
式中:S'表示当前搜索个体与当前最优解的距离;f表示螺旋形状参数;v表示值域范围为[-1,1]均匀分布的随机数。
(3)随机搜索模型的表达式为
式中:S''表示当前搜索个体与随机个体的距离;Xrand(t)表示当前随机个体的位置。
使用WOA 方法优化ELM 模型输入层权值w和隐藏层节点阈值h两个参数,并形成WOA-ELM模型。
2 基于SGMD-CMAE 和WOA-ELM 的滚动轴承故障诊断
基于SGMD-CMAE 和WOA-ELM 的滚动轴承故障诊断具体流程如下:
(1)用加速度传感器和振动信号采集卡搭建滚动轴承振动信号采集系统,通过滚动轴承实验平台分别采集滚动轴承内圈和外圈的故障振动信号。
(2)通过SGMD 分别对上述两种故障信号分解,得到多个SGC,并利用相关性准则,选择相关性高的SGC 重构信号。
(3)使用CMAE 计算重构信号的CMAE 值,并构造CMAE 特征。选用每种故障的CMAE 特征100 组,共200 组CMAE 特征。设定训练集与测试集的分配比例为8∶2,随机选择160 组CMAE 特征作为训练集,其余40 组CMAE 特征作为测试集,并将3 种故障信号的CMAE 特征集使用标签标记。
(4)采用WOA 优化ELM 模型中的输入层权值w和隐藏层节点阈值h两个参数。首先,随机确定ELM 模型中w和h的值;设置WOA 的种群规模s和最大迭代次数tmax,并初始化各个体坐标。然后,设迭代次数初始值t=0,将训练集的错误率作为适应度函数,计算初始时各个体适应度值,选出适应度值最小的个体。迭代次数t加1,更新有关参数,并生成随机数p∈[0,1],计算各个体下一步空间坐标。当a<1、p<0.5 时,采用逐渐搜索模型;当a<1、p≥0.5 时,采用螺旋搜索模型;当参数a≥1 时,采用随机搜索模型。当t≥tmax时,结束迭代,得到最优解。输出WOA 优化后的w和h两个参数,形成WOA-ELM 模型。
(5)将划分的CMAE 熵值特征训练集输入到WOA-ELM 模型中进行训练,并使用CMAE 熵值特征测试集预测滚动轴承故障类型,从而实现滚动轴承的故障诊断。滚动轴承故障诊断流程图如图7所示。
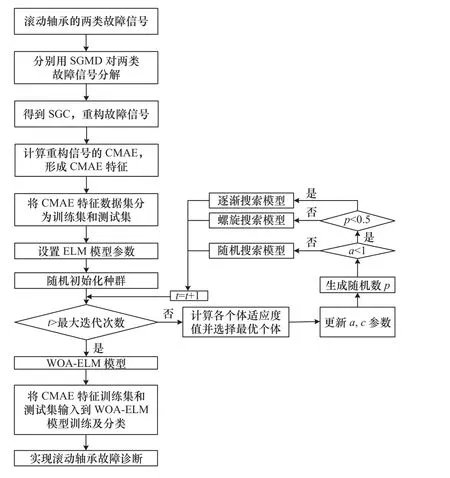
图7 滚动轴承故障诊断流程图
3 实验分析
3.1 滚动轴承故障数据的获取
使用的滚动轴承故障数据来自XJTU-SY 滚动轴承加速寿命试验数据集[17],该数据集的试验台如图8 所示。单向加速度传感器通过磁座固定在测试轴承的水平和竖直方向上,并通过便携式动态信号采集器采集滚动轴承内圈和外圈两类故障信号。其中,内外圈故障形式如图9 所示。
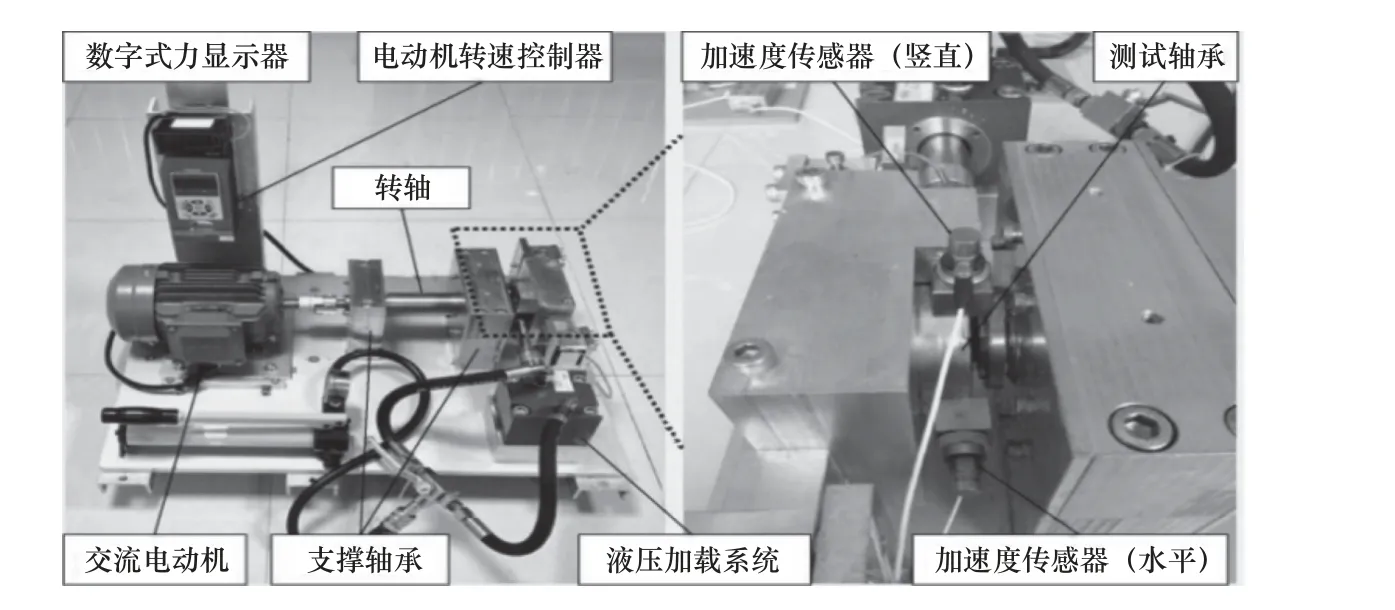
图8 轴承加速寿命试验台

图9 轴承内外圈典型失效类型的图片
参与实验的滚动轴承工况为转速2 400 r/min,径向力10 kN。通过计算得到内圈和外圈的理论频率分别为fi=184.50 Hz、fo=115.52 Hz。如图10 所示,图10a 和图10c 分别为内圈和外圈的故障信号时域图,图10b 和图10d 分别为相对应的频谱图。两种类型的故障频率特征被噪声所掩盖,无法得到有效信息。因此,采用SGMD 对各故障信号进行重构。
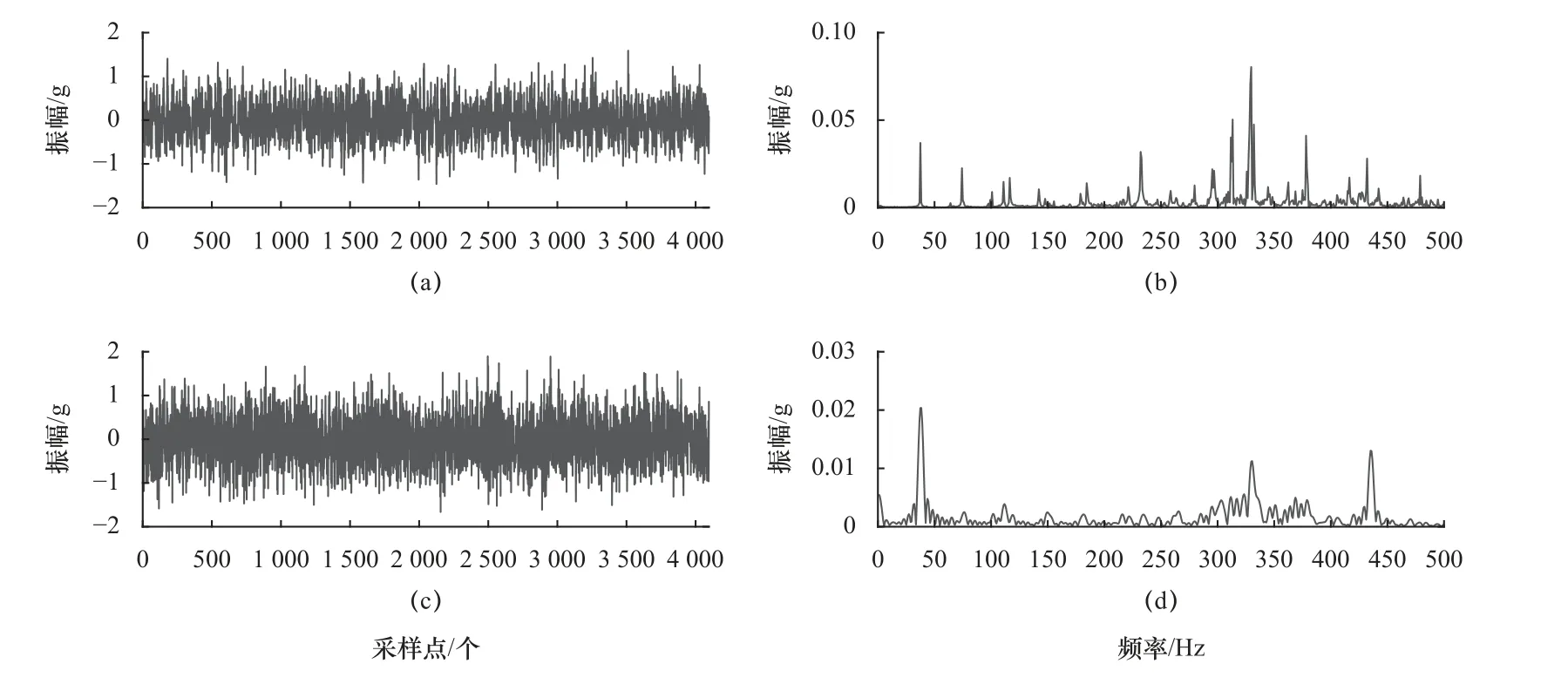
图10 滚动轴承故障信号时频图
3.2 SGMD 重构信号
通过SGMD 方法对滚动轴承内圈和外圈两种故障信号分解得到多个SGC 分量信号,如图11所示。
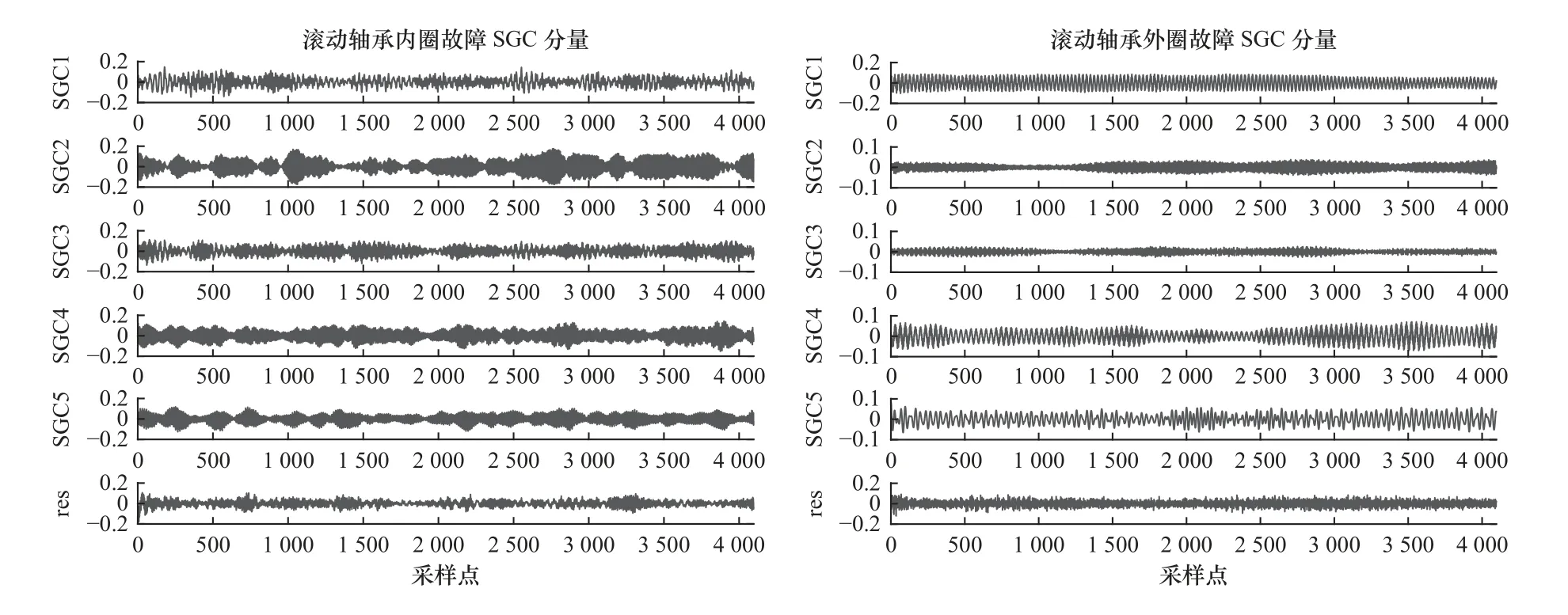
图11 滚动轴承两类故障信号SGC 分量
根据相关性准则,选取图11 中与故障信号相关性大的SGC 分量进行信号重构。各故障信号的SGC 分量相关系数见表1。根据反复实验选取相关系数阈值为0.80,故选取滚动轴承内圈和外圈故障信号SGC1、SGC2 和SGC3 分量重构。
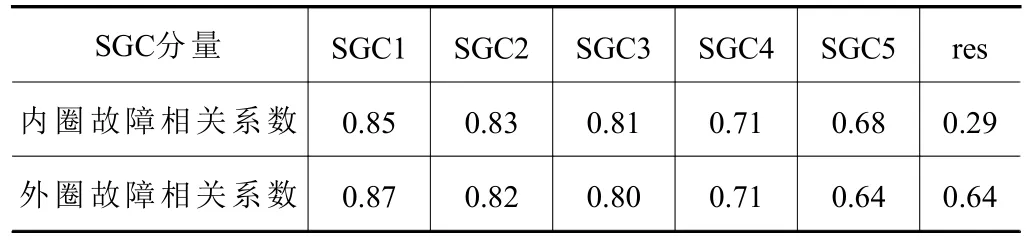
表1 各SGC 分量与原信号的相关系数
图12 所示为重构信号时频图。图12a 和图12c分别为滚动轴承内圈和外圈故障重构信号时域图,图12b 和图12d 是对应的频谱图。与图10 相比,图12 中的故障频率凸显,说明SGMD 方法能够有效重构故障信号,为下一步使用CAME 方法提取故障轴承故障特征奠定基础。
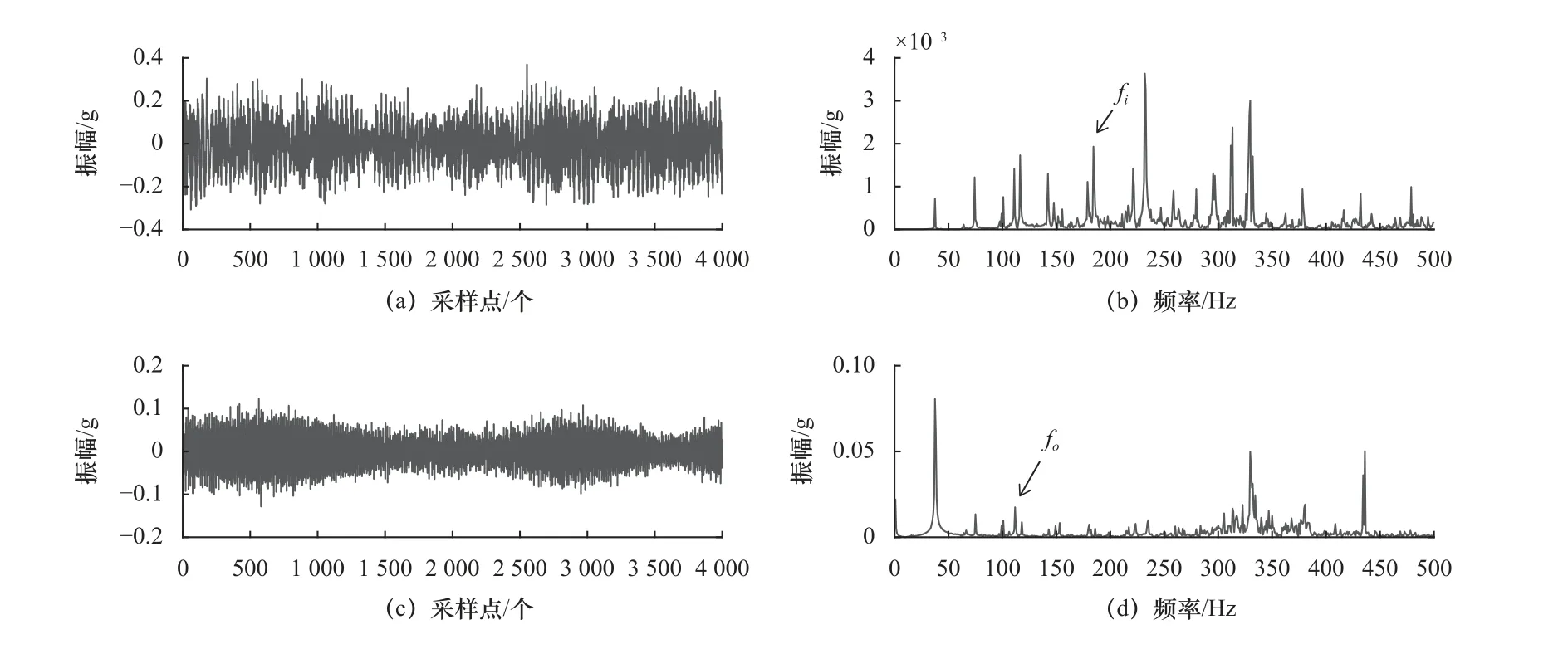
图12 两类故障重构信号时频图
3.3 CMAE 提取故障特征
采用SGMD 方法重构故障信号后,再通过MAE和CMAE 分别计算两类故障重构信号的MAE 熵值和CMAE 熵值。熵值分布结果如图13 所示。与MAE 方法相比,基于粗粒化不足改进的CMAE 方法更能有效地区分两种故障特征。在故障特征定量提取方面体现出明显的优势。
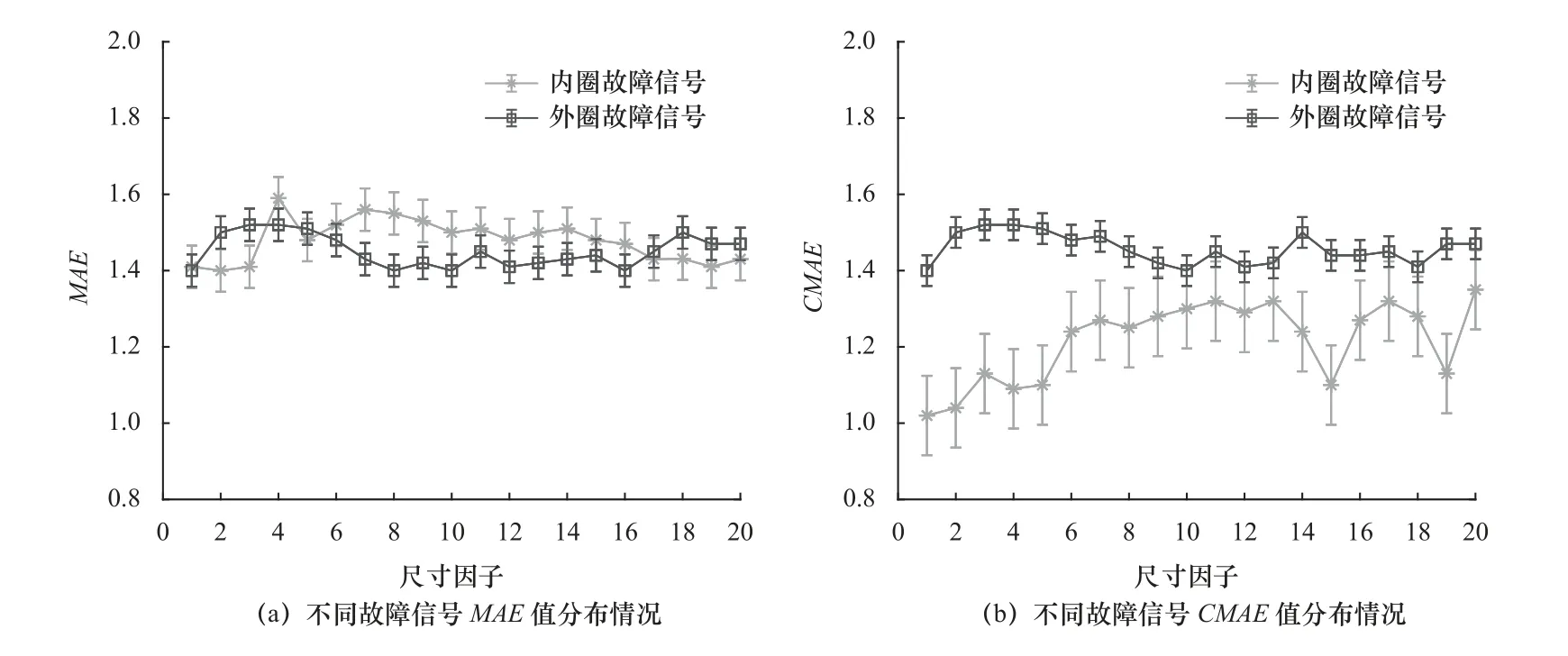
图13 不同故障信号的熵值分布情况
3.4 故障诊断
首先,采用SGMD 对滚动轴承两类故障信号进行重构,再通过MAE 和CMAE 方法分别计算重构信号的特征熵值,并用标签1 和标签2 标记。标签1表示滚动轴承内圈重构故障信号特征熵值,标签2表示外圈重构故障信号特征熵值。将两种故障类型熵值特征训练集160 组数据分别输入到ELM 模型和WOA-ELM 模型中训练,然后对测试集40 组数据进行分类。图14 所示为一次实验结果。图14a 中,SGMD-MAE-ELM 诊断模型对两种故障类别分类,标签1 和标签2 的正确率均为75%;图14b 中,MAE-WOA-ELM 诊断模型对两种故障类别分类,标签1 的正确率为90%,标签2 的正确率为100%,总体故障分类正确率为95%;图14c 中,SGMDCMAE-ELM 诊断模型对两种故障类别分类,标签1的正确率为95%,标签2 的正确率为100%,总体故障分类正确率为85%;图14d 中,SGMD-CMAEWOA-ELM 诊断模型对两种故障类别分类,标签1的正确率为100%,标签2 的正确率为95%,总体故障分类正确率为97.5%。
通过上述4 种模型的诊断结果,初步说明了SGMD-CMAE-WOA-ELM 模型能够提高滚动轴承故障的诊断准确率。
为了进一步验证所提模型的故障诊断性能,与有关的故障诊断模型进行了比较,重复多次试验取平均值,见表2。通过对表中数据的分析,得出以下结论:第一,对比EMD-MAE-ELM、VMD-MAEELM 和SGMD-MAE-ELM 模型的结果,在时间相近的情况下,SGMD-MAE-ELM 模型的故障诊断准确率最高,说明SGMD 方法能更好地分解故障信号,突出故障特征;第二,比较SGMD-SE-ELM、SGMD-PE-ELM、SGMD-FE-ELM 和 SGMD-MAEELM 模型的结果,分析得到MAE 方法提取滚动轴承故障特征的时间明显低于其他几种熵方法,说明了MAE 方法的优越性,同时,将SGMD-MAEELM 和SGMD-CMAE-ELM 模型进行比较,虽然在定量计算故障特征方面,CMAE 过程更为复杂,所需时间稍长,但在特征提取方面更为全面准确,使得整个故障诊断模型的准确率大幅提升;第三,将SGMD-MAE-ELM 和 SGMD-MAE-WOA-ELM、SGMD-CMAE-ELM 和 SGMD-CMAE-WOA-ELM 模型分别进行对比,能够清晰地看到WOA 可以有效地对ELM 模型进行优化,使得模型准确率更高。
4 结语
针对滚动轴承振动信号因信噪比不高而难以准确提取故障特征的问题,提出基于SGMD-CMAE和WOA-ELM 的故障诊断方法,并得到以下结论:
(1)SGMD 方法能对滚动轴承故障信号进行重构,提高信噪比,进而为故障特征的提取奠定基础。
(2)提出了利用CMAE 方法定量提取重构信号故障特征。与传统熵相比,CMAE 方法更能精准地提取滚动轴承故障特征,且计算速度较快。
(3)选用WOA 方法优化ELM 模型,构建WOA-ELM 模型。并利用WOA-ELM 模型对CMAE熵值特征进行训练和分类。与ELM 模型相比,WOAELM 模型对滚动轴承故障诊断的正确率更高。
本文所提的故障诊断方法能够识别滚动轴承不同故障类型,为滚动轴承故障诊断提供了新手段。
