A100 钢等效直角切削仿真及J-C 本构参数敏感度分析*
2023-12-11贾宗强白海清贾宗蒲
贾宗强 白海清② 贾宗蒲
(①陕西理工大学机械工程学院,陕西 汉中 723001;②陕西省工业自动化重点实验室,陕西 汉中 723001;③深圳久和自动化设备有限公司,广东 深圳 518100)
A100 钢(牌号 23Co14Ni12Cr3MoE)材料具有高强度、高硬度和高断裂韧性,以及很好的抗疲劳和抗应力腐蚀开裂能力,在航空领域被广泛应用[1]。但优异的材料性能也给A100 钢的切削加工带来了诸多难题,如在加工过程中容易出现粘刀现象,切削力大、切削温度高,加工表面质量差等[2-3]。在提高A100 钢切削加工性能的研究中,传统的试切实验成本高,且切削温度等响应变量难以测量,而利用有限元仿真可以代替传统的试切,得到实验中难以获取的参数[4]。材料本构参数的准确性,决定了仿真结果的精度[5]。获取材料本构参数的方法主要有3 种:有限元法、霍普金森压杆试验法和切削试验法。其中,压杆试验法是一种直接获取材料本构参数的方法,但结果精度不高,难以准确描述切削加工过程中的材料变形行为[6]。切削试验法通过金属切削理论得到切削区域的应力、应变和应变率等,从而逆向识别出较为准确的材料本构参数,但该方法依赖于正交切削实验,实验平台难以搭建。有限元法也是一种材料本构参数的逆向识别方法,与切削试验法相类似,其同样先根据压杆实验获得材料的本构参数值(是不精确的)作为基准值,并根据基准值确定本构参数的寻优范围,最后利用寻优算法在该范围内找到精确的材料本构,有限元法不受实现条件的限制,但不足之处是效率低下。有限元法逆向识别材料本构参数时,效率低下的原因有两个方面:第一,优化目标函数的建立是基于以各本构参数为设计变量所得试验方案下进行的切削仿真结果,由于本构参数较多,故所需仿真的次数也多;第二,因为三维仿真有限元模型网格众多,导致计算量巨大,所以单次的仿真时间也较长。
目前,在切削加工仿真研究方面,关于A100钢本构模型的公开资料较少。Johnson-Cook 本构模型(简称J-C 模型),综合考虑了材料在切削加工过程中的应变硬化、应变率硬化和热软化效应,且各参数容易通过实验获得,被广泛应用于金属切削加工领域。本构参数逆向识别方法即:将仿真结果和实验观测值进行比较,并不断调整本构参数,直到二者达到良好的一致性[7],是精确获取材料J-C本构参数的有效方法,被广大学者采用。李新建等[8]根据前人的工作,选择了对仿真结果影响显著的3个J-C 本构参数作为响应面仿真试验方案的设计变量,而对不显著的部分本构参数取固定值,大幅提高了Ti-6Al-4V 合金材料本构参数的优化效率。彭超等[9]通过在给定范围内不断改变并输入各本构参数的值进行仿真,将仿真值与实验真实值结合建立了二者的误差函数,并作为优化目标求解,利用单纯形优化算法逆向识别了钛合金粉末压制成形材料的本构参数。彭臣西等[10]利用二维切削仿真研究了7075 铝合金各J-C 本构参数对流变应力的影响规律,并对本构参数进行了优选。吴敏等[11]基于二维直角切削仿真模型,研究了材料本构参数对切削力、切削温度的影响规律,为铝合金本构参数的逆向识别提供了依据。
综上,为提高参数识别效率和精度,利用二维的铣削仿真模型和正交试验方案,研究了A100 钢JC 本构参数对仿真结果影响的显著性及规律。在利用有限元法逆向识别A100 钢的J-C 本构参数时,为本构参数及仿真模型的选择提供了理论依据和参考。
1 等效平面理论与等效参数值计算方法
切屑流出方向与刀具切削速度方向所在的平面即等效平面。在斜角切削过程中刀具与工件和切屑间的真实作用参数是等效平面内的等效参数。目前,对等效平面理论的介绍中,还缺少对刀具切削刃法向后角的准确描述,导致等效后角的计算表达式不够明晰。于是,有必要推导斜角切削的法向后角。为明确各个角度的位置关系,进行了图解分析,分别如图1、图2 所示。
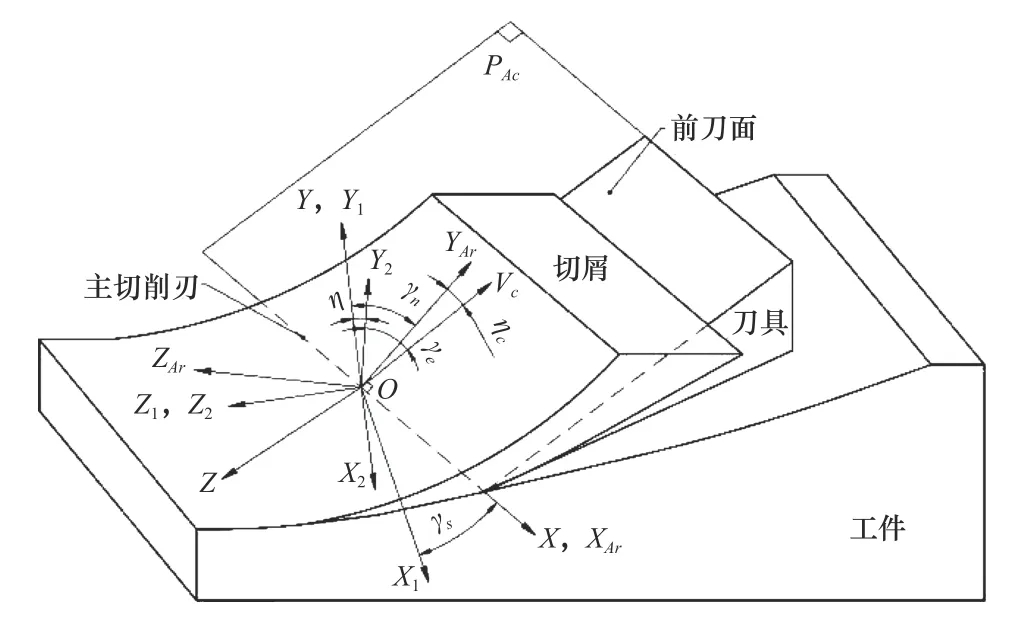
图1 斜角切削示意图
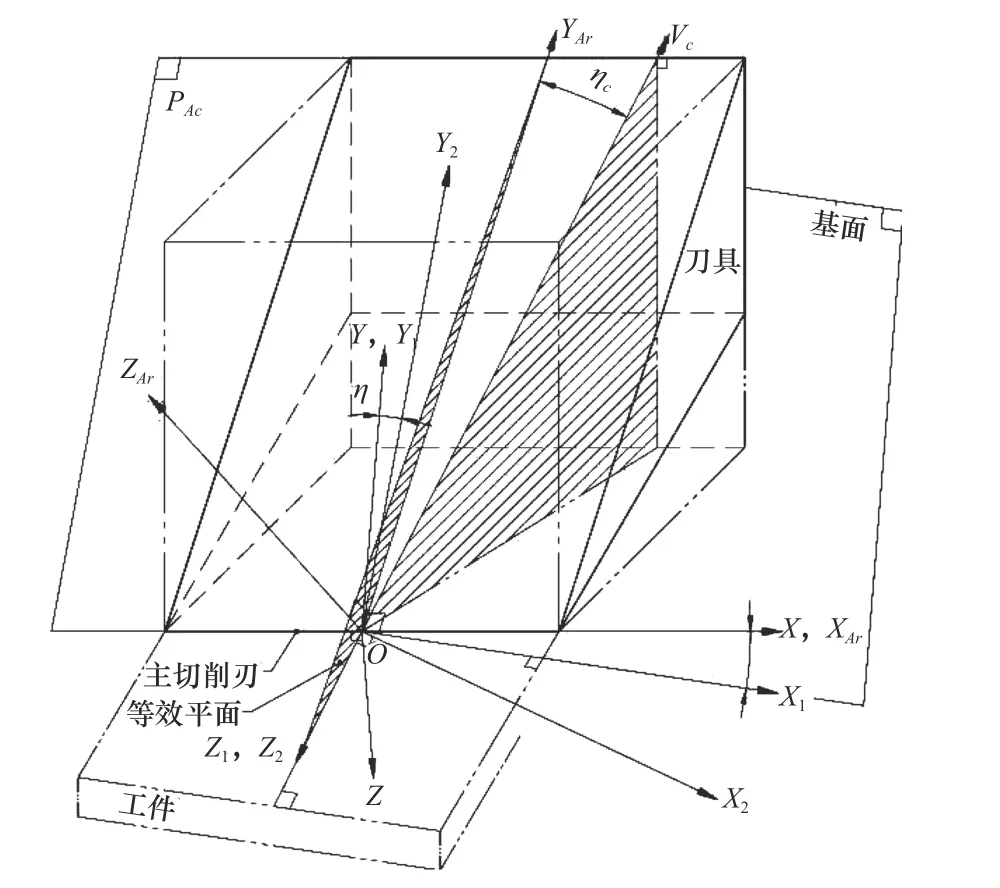
图2 坐标系位置变换关系图
在坐标系O-XYZ中,X轴是主切削刃所在直线、Z是主切削刃的法线所在直线。坐标系O-XArYArZAr由坐标系O-XYZ绕X轴旋转γn得到;坐标系O-X1Y1Z1由坐标系O-XYZ绕Y轴旋转 λs所得,Z1为刀具切削速度方向;同理,坐标系O-X2Y2Z2是由O-X1Y1Z1绕Z1旋转主方向角η得到。在图1 中,等效平面即 ∠YArOZ1。
1.1 等效后角
斜角切削中,切削刃的法向后角 αn、等效平面、后角 α0、刃倾角 λs及等效后角 αe、法向前角 γn的几何关系如图3 所示。其中,APQI为基面、APP′A′为切削平面、IAA′I′为主 剖面、IAB′为法剖面、AKE′为等效平面、ACDB为前刀面、AC为主切削刃且在APP′A′平面内,BD平行于B′D′且在IQQ′I′平面内,DD′在PQQ′P′平面内,BB′平行于DD′且与点I在同一条直线上。
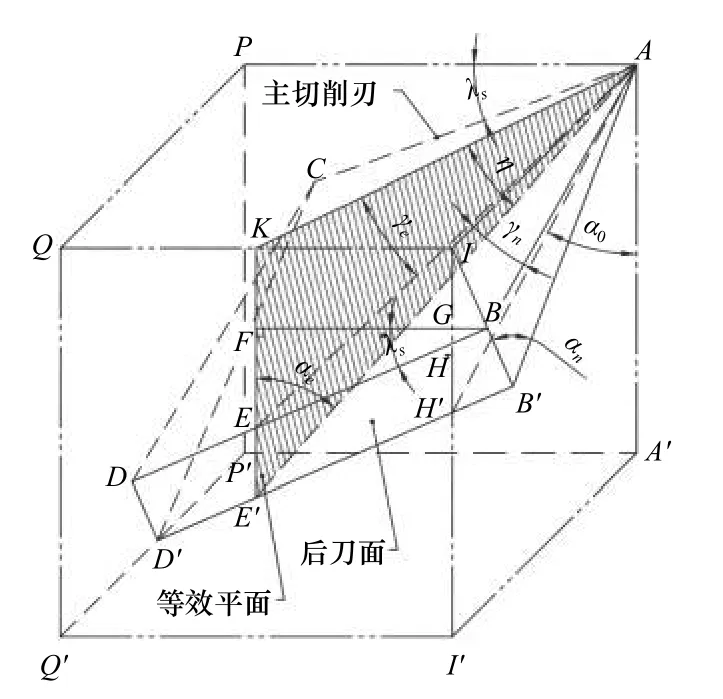
图3 法向后角几何关系图
法向后角的推导过程如下:
由图3 已知
联立式(1)、式(2)得
由于DB与D′B′平行,且均在IQQ′I′平面上,故由线段IB与BD垂直可知IB′垂直于H′B′,又由勾股定理可知:
联立式(4)、式(5)得
于是,可证明AB′垂直于H′B′,故有
联立式(1)、式(7)得
由IB′垂直于H′B′可知:
联立式(8)和式(9)得
由于线段DB、D′B′平行并与KE′相交于点H′、E′,且位于平面IQQ′I′上,结合线段BF与KE垂直、IB′与H′B′垂直,可知 ΔBEF相似于 ΔIB′H′,又知
联立式(10)、式(11)、式(12)得
于是,对于法向后角 αn有
故法向后角为
在铣削加工中,刃倾角 λs等于螺旋角 ω、法向前角 γn=arctan(tanγ0cosλs),其中 γ0为前角。结合文献[12]得到等效后角为
再参考相关文献[13]得到等效前角、等效刃口钝圆半径等。
1.2 等效前角
1.3 等效刃口钝圆半径
式中:rn为钝圆半径、γn为法向前角、λs为刃倾角。
1.4 等效切削厚度和等效切削宽度
(1)等效切削厚度(即每齿进给量)
(2)等效切削宽度
2 正交试验
如图4 所示,以飞机上一种A100 超高强度钢材料的万向接头为研究对象,其材料物理性能见表1,毛坯分别用端面铣刀和立铣刀经粗铣、精铣最后镗孔及磨削完成加工,对加工表面质量要求较高。为了提高仿真效率,笔者采用硬质合金立铣刀顺铣,刀具直径为8 mm,铣刀螺旋角ω为20°,切削刃前角 γ0为5°,后角 α0为30°,刀尖钝圆半径为0.04 mm;采用侧铣加工方式,轴向切深为1.5 mm,径向切宽为2 mm,切削速度为40 m/min[14],每齿进给量为0.05 mm,环境温度为20 ℃。分别根据式(16)、式(17)、式(18)、式(19)、式(20)得等效二维铣削加工仿真模型各参数见表2。
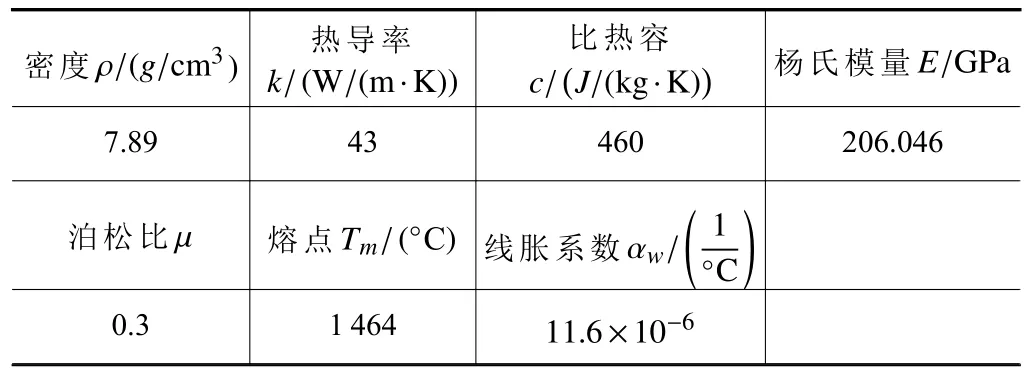
表1 A100 钢材料物理性能[3,15]

表2 等效后铣削加工参数
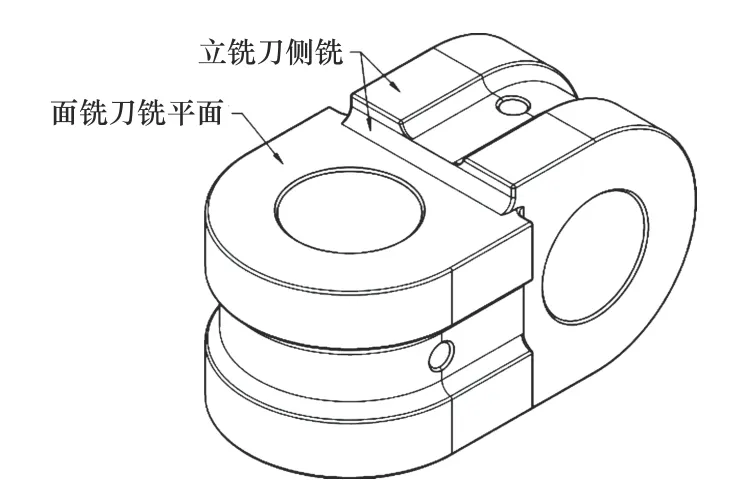
图4 万向接头
2.1 有限元仿真
有限元仿真模型采用自适应网格划分技术,在刀具切削刃和工件被加工表面进行了网格加密。网格单元尺寸最大值为1 mm、最小值为0.1 mm,最小边长为2×10-4mm,边长递减梯度为0.5。等效后的铣削加工有限元仿真模型与等效前对比如图5所示。

图5 仿真模型示意图
2.2 正交试验设计
J-C 本构参数是由Johnson Gordon R 和William H Cook 提出的半经验塑性金属材料模型,其表达式如下[16]:
其中:σ为流动应力,即材料进入塑性状态后材料的 实时屈服应力,单位为MPa;和分别为等效应变率和参考应变率,一般在应变率较大时取参考应变率为1;T0和Tmelt分别为室温和材料熔点;T为实时工作最高温度;A、B、C、m、n为J-C 本构参数。其中:A为初始屈服应力、B为应变强化系数,C为应变率强化系数,m为温度热软化系数,n为加工硬化指数。
目前,对A100 钢J-C 本构参数准确描述的公开资料相对较少,但由于A100 钢是我国基于美国在1991 年研制的Aermet100 钢基础上开发的,性能上与之较为接近,故此处将其本构参数值作为A100 钢本构参数的初始值,并认为A100 钢的本构参数在包括该初始值的一个区间范围内。初始值的情况见表3。

表3 A100 钢J-C 本构参数初始值[17]
在本构参数逆向识别中,没有直接的方法来确定参数的取值范围,往往只是由理论分析或经验来估计。由于此时尚不知各参数的显著性,故可以先适当地将取值范围选大一点。采用L25(56)正交表设计有限元模拟方案,其因素水平安排见表4。
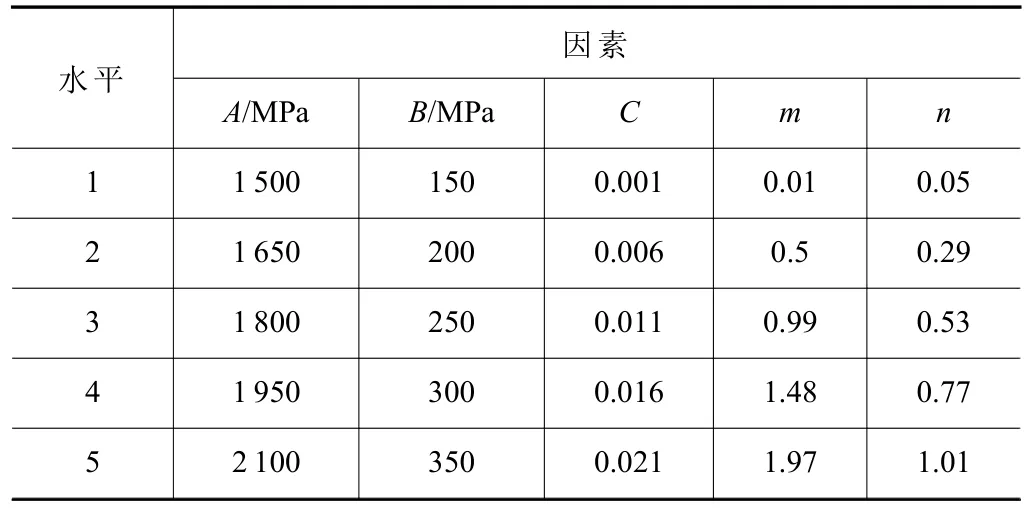
表4 J-C 本构参数因素水平表
3 试验结果分析
3.1 正交试验结果
在其他条件相同的情况下,分别利用有限元分析软件按照正交表安排的本构参数组合,进行等效二维铣削模型仿真(2D)和对应的三维铣削模型仿真(3D),并分别统计铣削力和铣削温度。
其中铣削力指的是水平方向的主切削力,如图6所示,由于是顺铣,故主切削力为Fx。铣削温度,指的是铣削过程中刀尖最高温度。正交试验方案及所得仿真结果分别见表5 和表6。
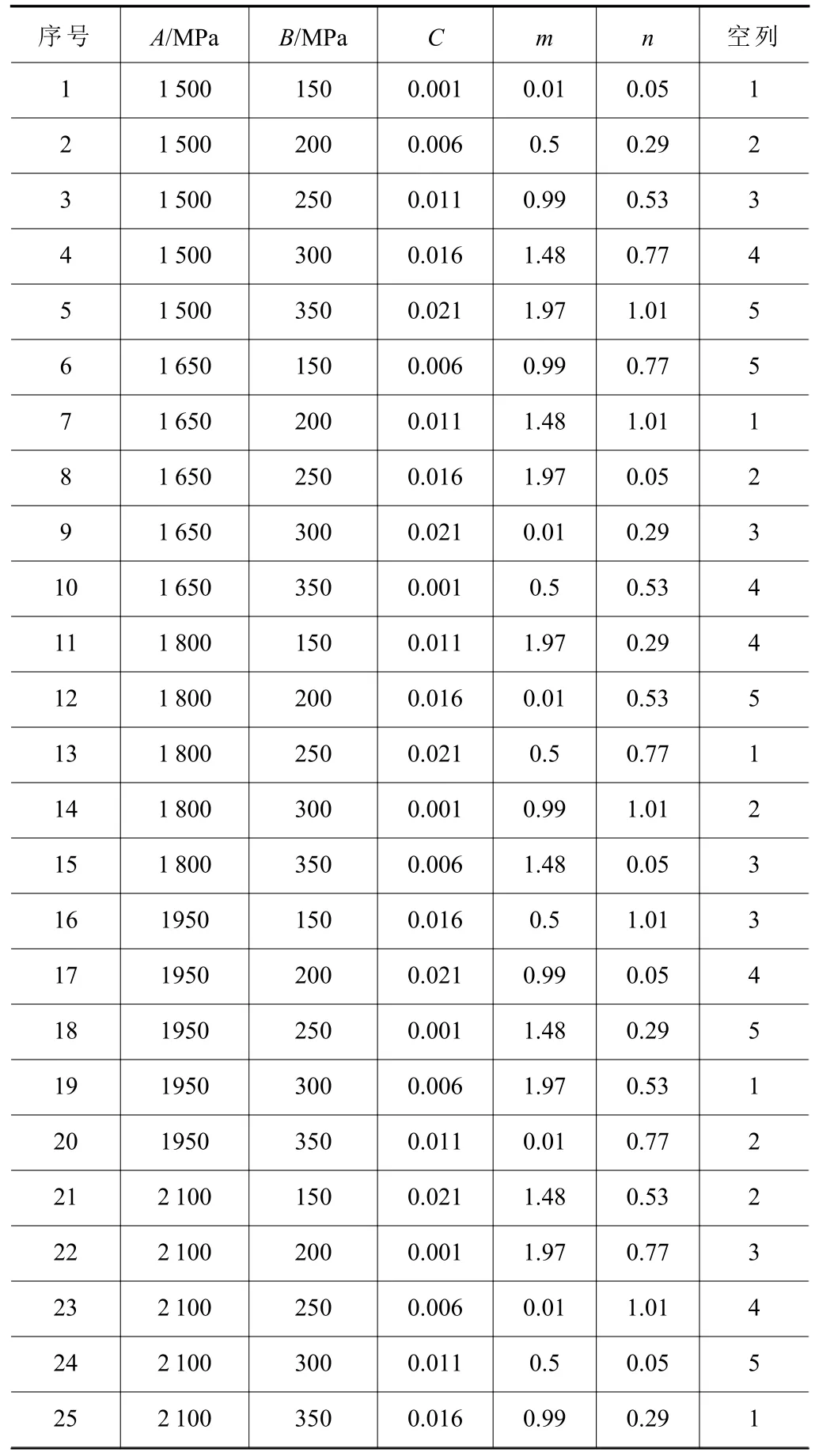
表5 正交试验方案
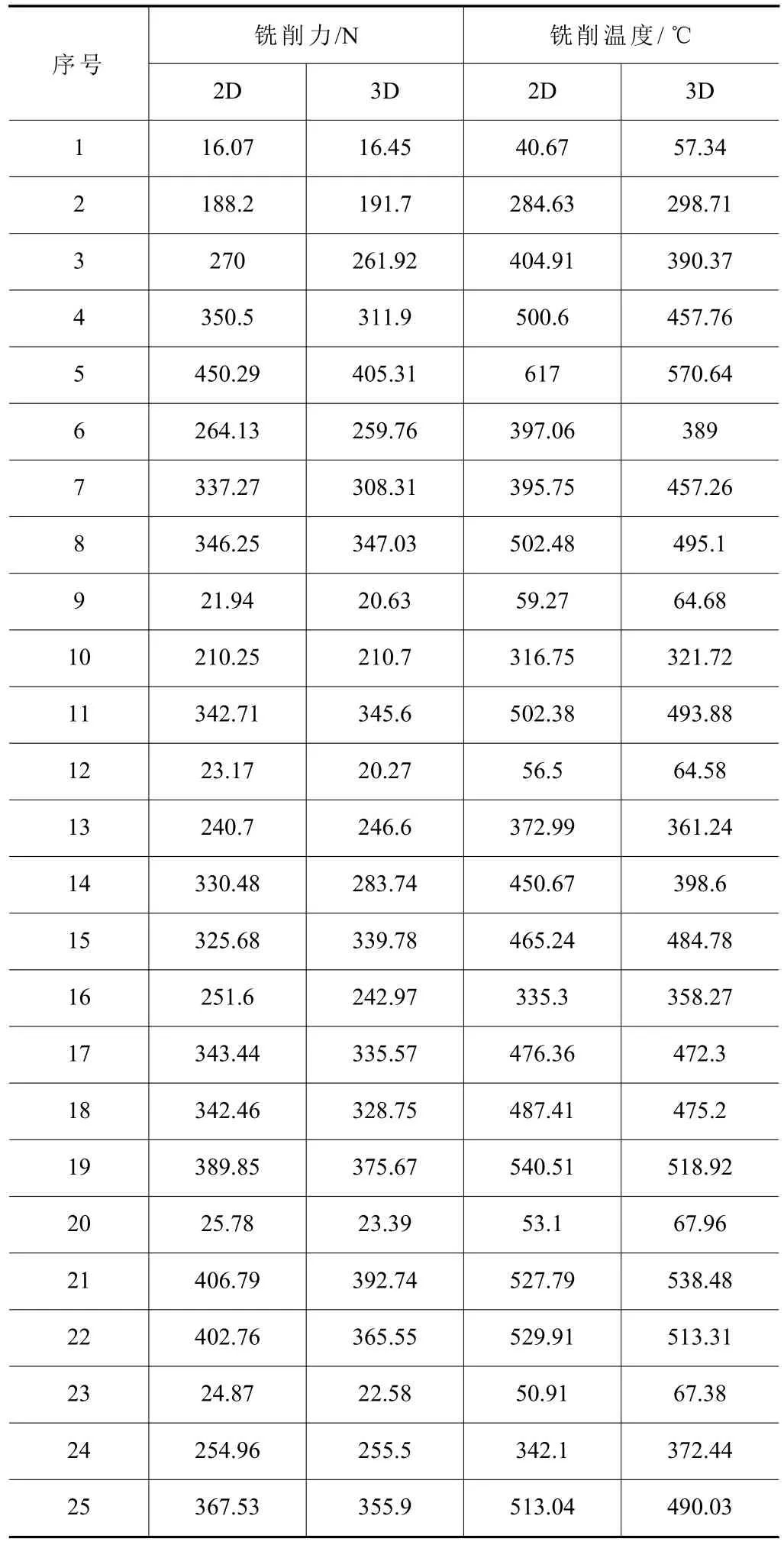
表6 正交试验结果
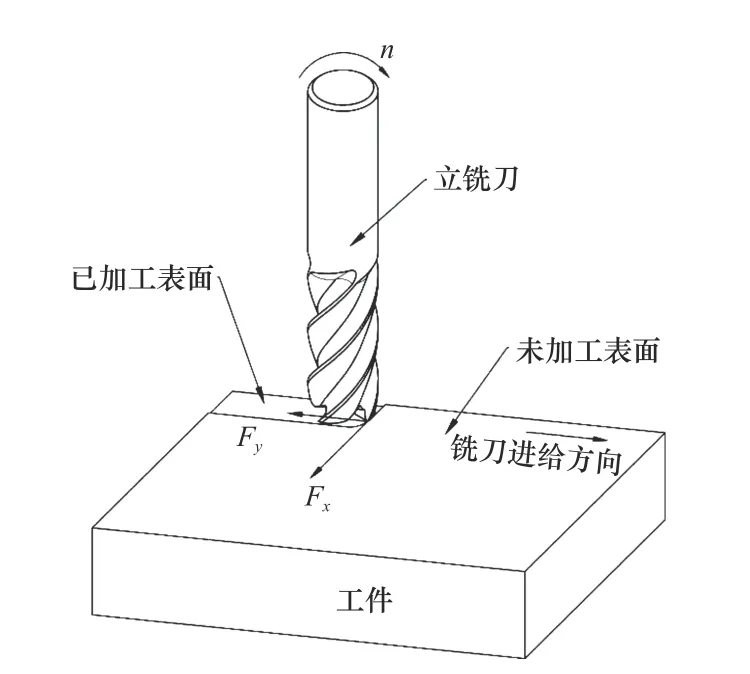
图6 铣削力示意图
将2D 仿真结果的铣削力记作F2D,铣削温度记作T2D;同样,把3D 仿真结果的铣削力和铣削温度分别记作F3D、T3D。
下面分别对F2D和T2D做极差、方差分析,研究各J-C 本构参数对铣削力、铣削温度的影响规律。
3.2 极差分析
极差分析法是一种直观的分析方法,可以通过极差分析的“主效应图”观察某一个响应变量均值随各因素水平的变化规律,通过均值曲线斜率和极差来粗略地说明各设计变量对响应变量的影响大小。均值和极差的计算方法如下:
(1)响应变量均值
式中:Kij为第i个设计变量取j水平时所对应响应变量值的和;s为水平数,在这里易知s=5。
(2)极差
式中:Ri为设计变量i的极差,在这里i分别为本构参数A、B、C、m、n。
通过式(22)和式(23)得到铣削力F2D的主效应图如图7 所示。

图7 铣削力 F2D主效应图
利用同样的方法,可以得到铣削温度T2D的主效应图如图8 所示。

图8 铣削温度 T2D主效应图
可以看出铣削力和铣削温度的主效应图十分类似,在J-C 本构参数中,对铣削力和铣削温度影响最大的是m。随着m的增大铣削力不断增大;随着A和C的增大,铣削力、切削温度先减小后增大;B和n的变化对铣削力和铣削温度无显著影响。
3.3 方差分析
通过极差分析只能粗略判断各设计变量对响应变量影响的大小顺序,但并不能准确描述其显著性大小。于是这里就引入了对铣削力F2D以及铣削温度T2D的方差分析,分析结果分别见表7、表8。
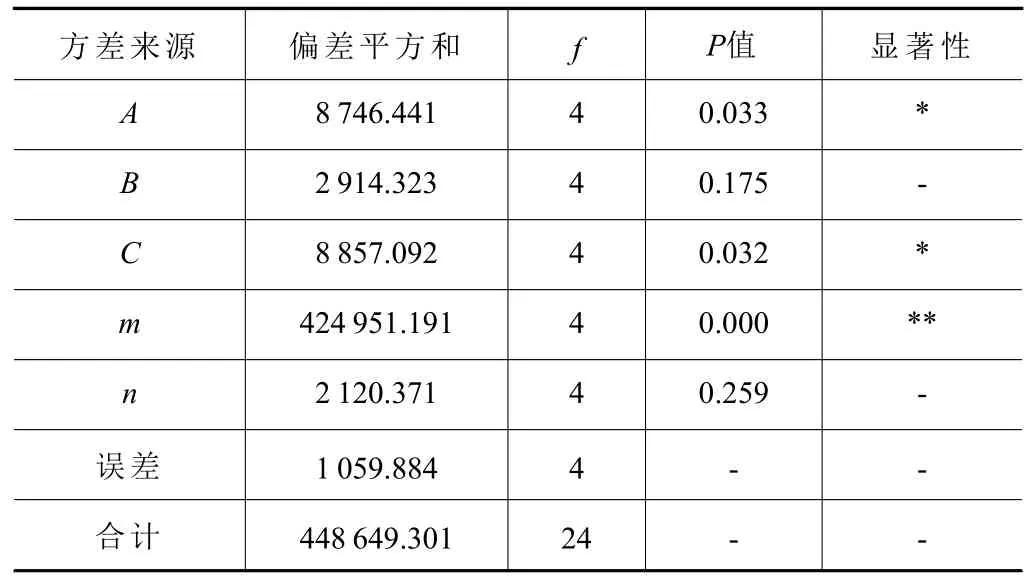
表7 F2D仿真结果方差分析

表8 T2D仿真结果方差分析
从方差分析结果可以看出,m对F2D和T2D的影响最大,同时A和B也都对其有显著影响,且显著性相当,与主效应图相符。
结合公式(21)可知,A100 钢材料的铣削力和铣削温度受热软化作用m的影响较大,说明m敏感度最高;其次,由B、n不显著,说明了该材料的加工硬化现象不明显,B、n敏感度最低。若以霍普金森压杆实验结果作为参考值进行本构参数逆向识别,在确定识别范围的时候可以将m的范围适当取大,A和C适当取小,B、n固定取参考值。
4 等效二维仿真模型适用性分析
灰色关联度分析方法可以同时考虑多个响应变量,将多个响应变量序列转化为单个的灰色关联度序列。这里,为验证所建等效二维铣削仿真模型的适用性,引入了灰色关联度理论,以便同时比较两种模型仿真结果的铣削力和铣削温度(即:同时比较F2D、T2D与F3D、T3D),具体实现过程如下:
4.1 无量纲化
4.1.1 响应变量矩阵
在灰色关联度计算中,假设有j个响应变量和i个试验方案,则响应变量矩阵Y如下:
4.1.2 数据归一化
为了便于比较和分析,消除量纲不同的影响,需要将数据做归一化处理,使得统计数据控制在0~1 范围内。在灰色关联度分析过程中,根据目标属性的不同,归一化处理的方法也不同。通常,目标属性分为两种类型:一是“望大型”(即期望目标值越大越好);二是“望小型”(期望越小越好)。
(1)望大型数据归一化方法
(2)望小型数据归一化方法
同上,j表示第j个目标(即响应变量),i是总的试验次数,k=1~i。
易知,铣削力和铣削温度都属于望小型响应变量,由式(26)可得归一化后的数据。归一化前、后数据分别见表9、表10。

表9 铣削力数据归一化结果统计
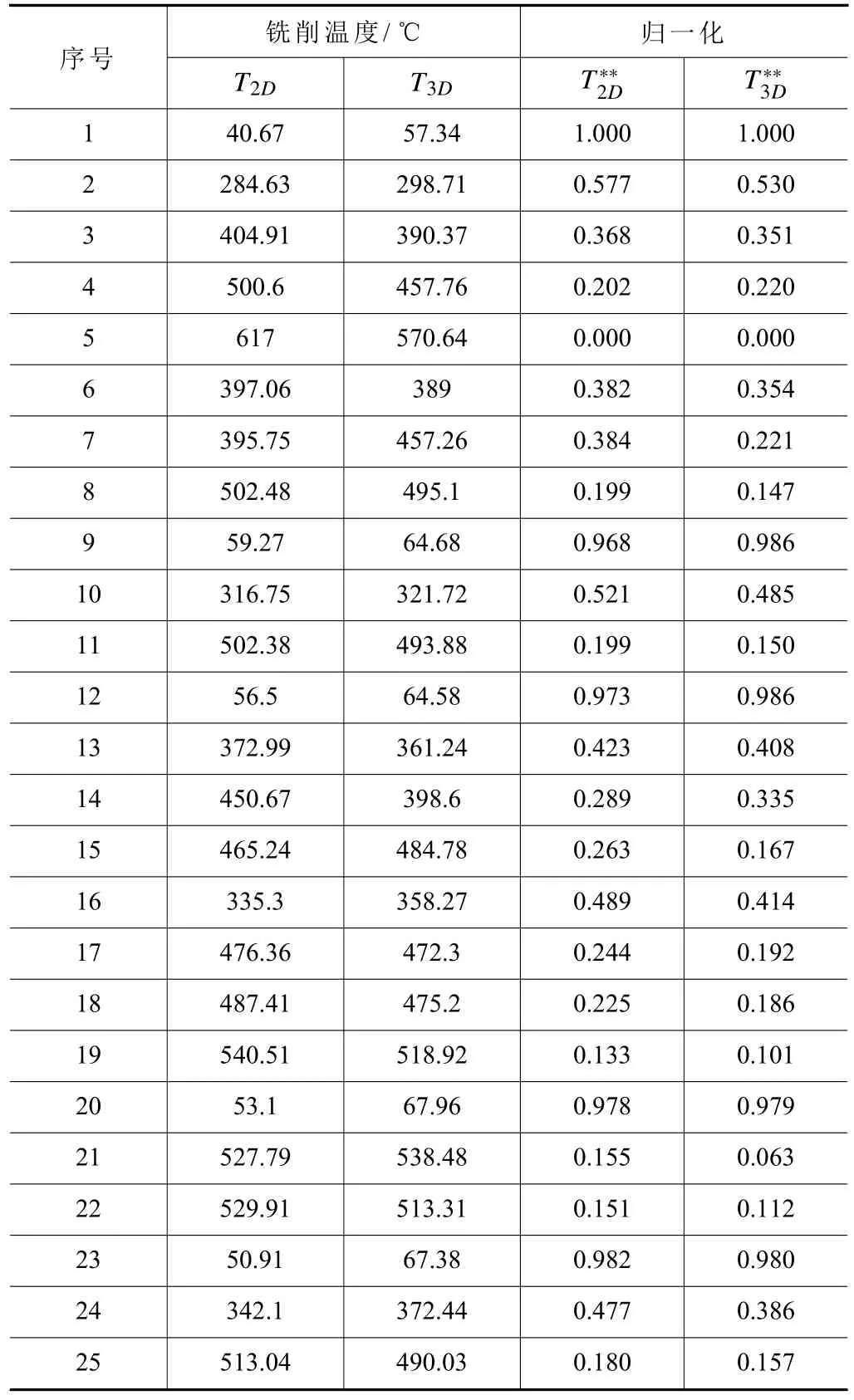
表10 铣削温度数据归一化结果统计
4.2 灰色关联系数与灰色关联度
响应变量作为一个比较序列,灰色关联系数(grey relational coefficients,GRC)表示比较序列和参考序列在某一时刻的关联程度。若记参考序列和比较序列在某一时刻数值差的绝对值为Δj(k)=则灰色关联系数的计算方法如下:
其中,y0(k)为参考序列,由于在数据归一化后,切削力和切削温度的最优值均为1,故y0(k)=[1,1,···,1]i1,ρ为分辨率,通常取0.5[18]。
灰色关联度是建立在灰色关联系数矩阵基础上,计算某一时刻灰色关联系数的平均值,最后得到一个灰色关联度序列,这个序列在0~1 区间内,其越接近于1 表示越理想。计算方法如下:
在式(28)中,βj为第j个响应变量的权重,结合以上分析,这里认为力和温度的权重相等。由式(27)可得灰色关联系数分别见表11和表12。
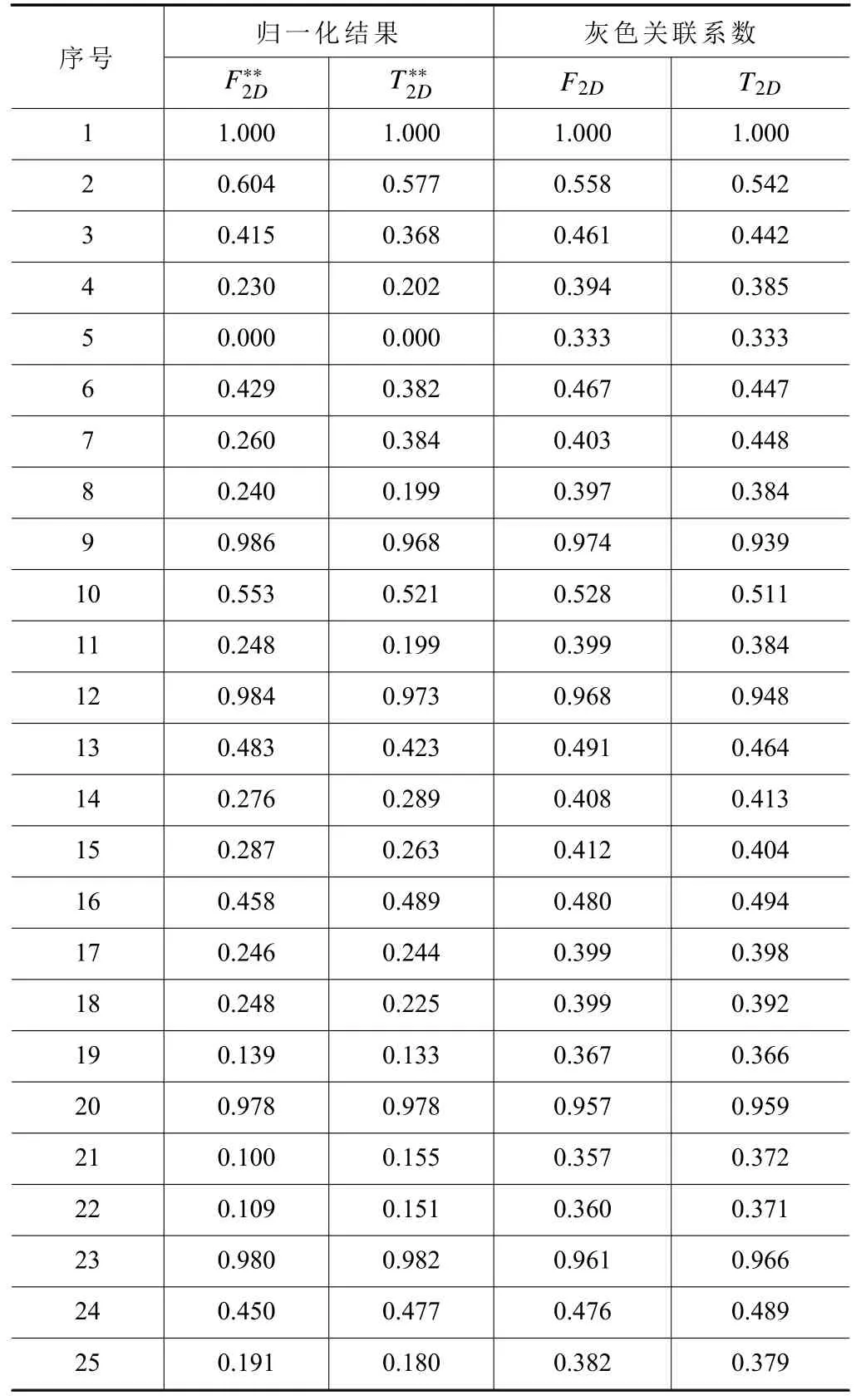
表11 等效二维模型仿真结果的灰色关联系数
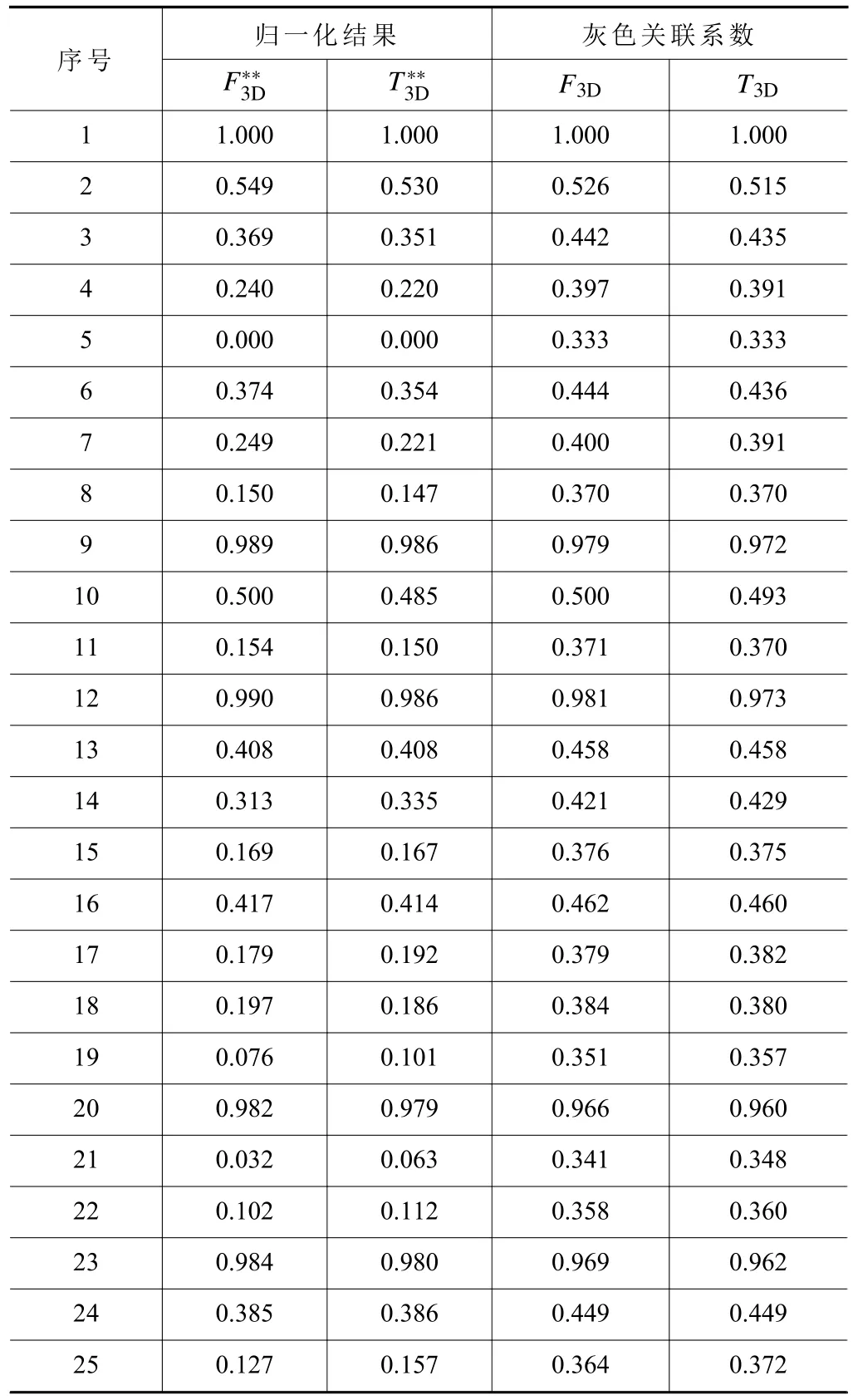
表12 原三维模型仿真结果的灰色关联系数
此处,令r1为F2D、T2D相对于参考数列的灰色关联度,r2为F3D、T3D的灰色关联度,于是由式(28)得到灰色关联度分析结果如图9 所示。
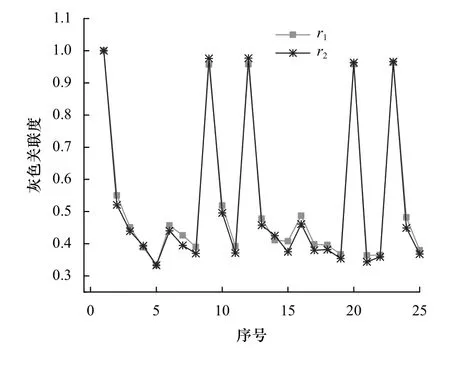
图9 灰色关联度分析结果
从图9 可以发现,灰色关联度r1和r2的变化规律和数值大小高度一致,说明所建立的等效二维铣削仿真模型具有很好的适用性。在后续的金属切削仿真研究中可以利用等效二维模型仿真效率。
5 结语
(1)推导出了螺旋铣刀切削刃法向后角关于主后角和螺旋角的转换关系,进而得到了等效后角的显示表达式。并结合相关文献给出了等效二维铣削模型,各种等效参数值的计算方法。
(2)在A100 钢J-C 本构参数中,热软化系数m的敏感度最高,在对其本构参数逆向识别时应当在较大寻优区间内取值,且取值精度也应增加。为提高识别效率,可忽略不敏感项B、n。
(3)等效二维铣削仿真模型可以很好的代替三维仿真模型,是保证本构参数逆向识别精度并提高工作效率的有效途径。
