螺旋槽磨削砂轮磨损轮廓模型与位姿补偿算法*
2023-12-11阳智麾
阳智麾 李 勇 刘 浩 江 磊
(西南交通大学机械工程学院,四川 成都 610031)
螺旋槽作为立铣刀的重要结构特征,对刀具的切削、卷屑、断屑以及整体刚性起至关重要的作用,因此其磨削工艺成为刀具加工的重点和难点[1]。在螺旋槽实际加工过程中,一片全新或修整的砂轮首先会进入快速磨损期间,然后进入稳定磨损期[2],因此砂轮磨损问题在螺旋槽磨削工艺中无法避免。对砂轮的磨损情况进行计算,并对其磨削位姿进行调整以提高螺旋槽加工精度具有很强的实际工程意义。
立铣刀螺旋槽的结构参数大多都是在径向截面下定义的,因此其径向截面轮廓的成形计算方法是螺旋槽磨削工艺的理论基础。目前主要采用解析法[2-3]、离散法[4-5]和布尔法[6]3 种方法。基于此,许多学者针对螺旋槽磨削工艺展开了大量研究,主要分为以下两类。
为了满足刀具特定的卷屑、断屑等需求而设计特定结构形状的螺旋槽,需要设计砂轮形状以满足螺旋槽加工要求,即成形砂轮磨削工艺(已知螺旋槽轮廓+砂轮位姿→计算成形砂轮轮廓)。Karpuschewski B等[7]利用螺旋槽曲面法矢量必定与砂轮轴矢量接触原理,计算旋槽曲面与砂轮回转面之间的接触线。李国超等[8]在此基础上分析砂轮母线奇异点和端点位置与螺旋槽曲面的接触情况,完善成形砂轮轮廓计算方法。成形砂轮磨削工艺由于对砂轮轮廓精度要求较高,需要不断修整砂轮以满足轮廓设计要求,大大增加了加工成本。
将刀具螺旋槽进行参数化建模,选用标准砂轮,计算砂轮磨削位姿获得满足设计的槽型,即标准砂轮磨削工艺(已知螺旋槽参数化模型+砂轮轮廓→计算砂轮位姿)。Karpuschewski B 等[7]以砂轮位姿为优化变量、螺旋槽轮廓误差为优化目标。李国超等[8]在此基础上提出基于双斜面型砂轮尺寸和位姿组合优化的磨削工艺,根据螺旋槽轮廓曲线选用特定砂轮,并建立螺旋槽结构参数以及轮廓误差的优化目标函数,采用粒子群等优化算法进行求解。李海宾等[9]针对粗铣刀分屑槽形状的磨削工艺,对粗铣刀周齿分屑槽结构参数进行了定义,建立了加工坐标系及切深引导曲线方程。曾滔等[10]针对于解析法求解接触线难以在三维软件中实现参数化等问题,提出一种基于极限思想求解螺旋槽磨削接触线的几何方法。Chen Z 等[11]针对结构较为复杂的螺旋槽,提出一种通过两次磨削的方法控制螺旋槽的几何参数,包括前角、芯厚半径和槽宽。唐军等[12]提出了适用于参数化结构和位置定义的分屑槽数控磨削工艺,推导了相应的砂轮磨削轨迹算法,并基于得到的磨削轨迹和五轴数控工具磨床运动原理。熊建军等[13]通过定义容屑槽的结构参数、坐标系、坐标系变换矩阵以及砂轮初始姿态,并计算了砂轮的磨削轨迹。在此基础上,借助运动学原理基于工件坐标系的砂轮磨削位置和姿态的计算方法,采用坐标变换矩阵描述砂轮运动方式。标准砂轮磨削工艺重点在于计算砂轮位姿以获得指定槽型,以其高效、成本低、换型快的特性广泛应用于刀具螺旋槽的加工,也一直是研究的热点问题。
综上所述,虽然螺旋槽磨削工艺的研究较为成熟,但是现有的算法都未考虑砂轮实际磨损问题,仅将砂轮端面做棱边倒圆处理,忽略了对磨削过程中砂轮磨损情况分析,需要根据工人经验不断调整圆角大小重新计算砂轮磨削位姿,导致算法在实际应用中误差越来越大。本文针对砂轮在螺旋槽磨削过程中出现的不规则磨损情况,通过已加工螺旋槽轮廓反算磨损砂轮轮廓,提出一种基于砂轮实际磨损情况的螺旋槽磨削位姿调整算法(已知加工的螺旋槽+砂轮位姿→计算砂轮磨损情况+已知螺旋槽结构参数→计算砂轮调整位姿),并通过实际加工试验验证了算法的有效性。
1 计算不规则磨损砂轮轮廓
在螺旋槽实际加工中,由于前刀面磨削量最大,且砂轮越靠近边缘越脆弱,砂轮呈现不规则磨损状态,计算砂轮实际轮廓对后续砂轮位姿调整至关重要。
1.1 磨削运动建模
为了方便描述砂轮与刀具的磨削关系,定义以下坐标系及参数,如图1 所示。
(1)工件坐标系OW-XWYWZW,其坐标原点OW位于刀具端面圆心,坐标轴ZW与刀具轴线重合,坐标平面XWYW与刀具端面重合。
(2)砂轮坐标系OG-XGYGZG,其坐标原点OG位于大端圆的圆心位置,坐标轴ZG与砂轮轴线重合,坐标平面XGYG与砂轮大端圆平面重合。
(3)砂轮位姿参数VecX(ax,ay,α),其中ax、ay为原点OG在坐标平面XWYW的初始坐标(定义ax为中心距、ay为偏移距)、α为砂轮绕坐标轴XW旋转的角度(定义α为安装角)。本文定义砂轮的位姿都是初始状态下砂轮位置和姿态,然后在螺旋刃线引导下运动为砂轮磨削轨迹。砂轮坐标系与工件坐标系关于砂轮位姿参数VecX的变换矩阵MG-W可表达为
设立铣刀的螺旋刃线与刀具半径为RW、螺旋角为β,其磨削过程可以看作刀具固定不动、砂轮沿螺旋刃线引导下运动,即砂轮绕坐标轴ZW旋转的同时沿着其移动。因此,砂轮旋转角度ξ后,其相对于初始位姿(即砂轮圆心位于工件坐标系坐标平面XWYW)的运动变换矩阵Me(ξ)可表达为
式中:κ=RW/tanβ。
1.2 磨损砂轮轮廓求解
砂轮由于回转体的特点,将砂轮轮廓绕轴线旋转一周即可以得到砂轮回转面方程,因此计算磨损砂轮轮廓对于位姿调整至关重要。本文根据磨损砂轮加工的螺旋槽径向截面轮廓,采用成形砂轮计算方法[12]反算磨损砂轮的母线方程,螺旋槽磨削过程中螺旋槽曲面与砂轮回转面呈线相切接触,其接触线上点的法矢量必定与砂轮轴线接触(即矢量nQ、ZG、nQG共面),如图2b 所示。计算流程如下。
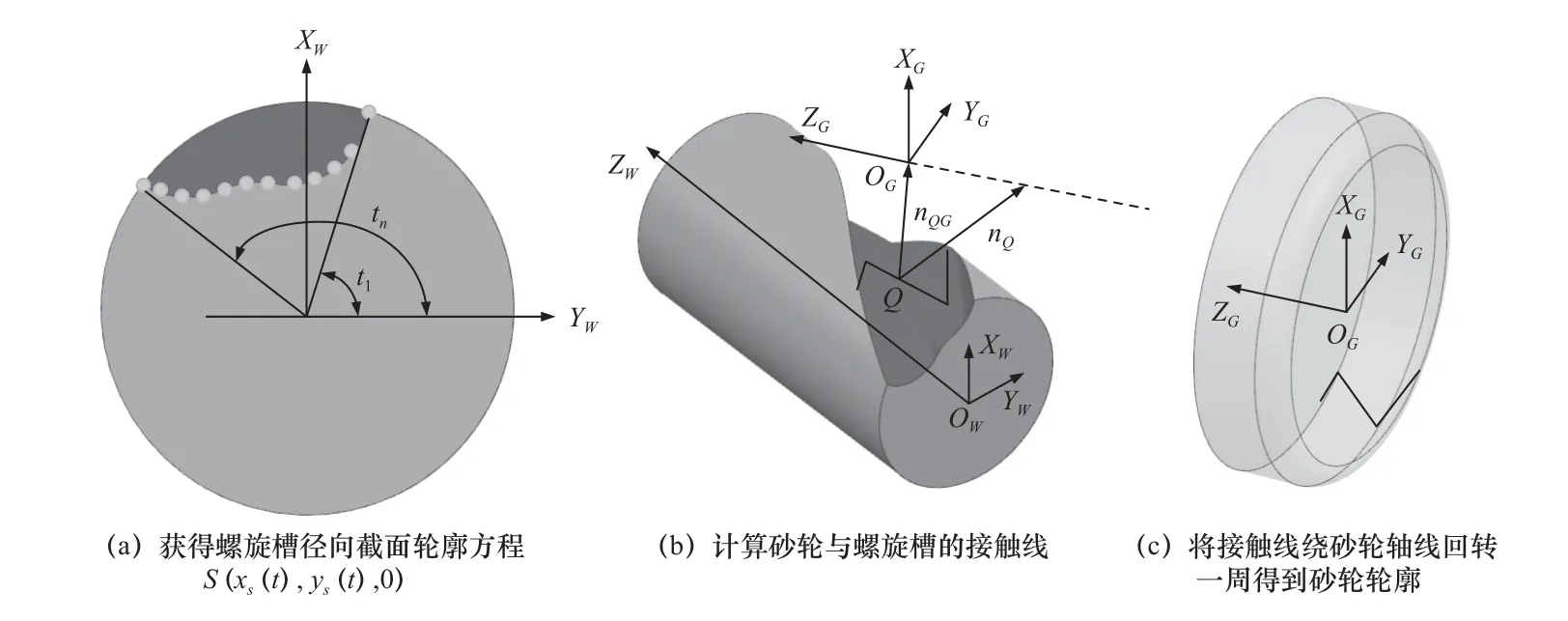
图2 磨损砂轮轮廓的反算流程
(1)在工件坐标系平面XwYw内,通过刀具轮廓检测仪测量得到加工的螺旋槽径向截形轮廓n个点坐标Si(xi,yi,0),通过插值方法获得已加工螺旋槽的径向截形轮廓程S(xS(t),yS(t),0),t1≤t≤tn,并在螺旋刃线引导下建立坐标系下的螺旋槽曲面方程Q(t,ξ)。
式中:t为螺旋槽轮廓方程的变量。
因此,螺旋槽曲面上任意点Q指向砂轮坐标原点OG的矢量nQG可表达为
(2)对螺旋槽曲面方程Q(t,ξ)变量分别求偏导,并叉乘得到螺旋槽曲面的法矢量nQ。
根据砂轮安装角α可知砂轮轴矢量ZG(0,-sinα,cosα),由矢量nQ、ZG、nQG共面建立接触线求解方程。
由式(6)建立的接触线求解方程在无限区间内有无穷个解,求解区间的预估对于求解稳定性至关重要。当求解区间预估错误时,一是会出现无解的情况;二是计算出来的砂轮轮廓可能会将螺旋槽轮廓内部实体当作磨削部分,如图3 所示。
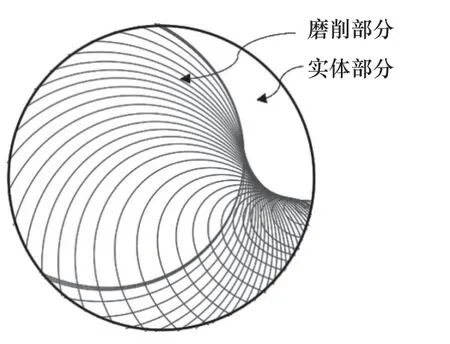
图3 砂轮轮廓求解错误情况
触线求解区间与砂轮安装位姿直接相关,砂轮位姿偏移距ay越往左侧偏移,求解区间整体向上偏移越大,同理,砂轮向右侧偏移则相反;砂轮位姿安装角α越大,接触线求解区间也会被拉长,如图4a所示。将砂轮与工件投影至平面XWYW上,砂轮由于绕XW轴旋转被压缩成椭圆面,刀具棒料为圆面,如图4b 所示。
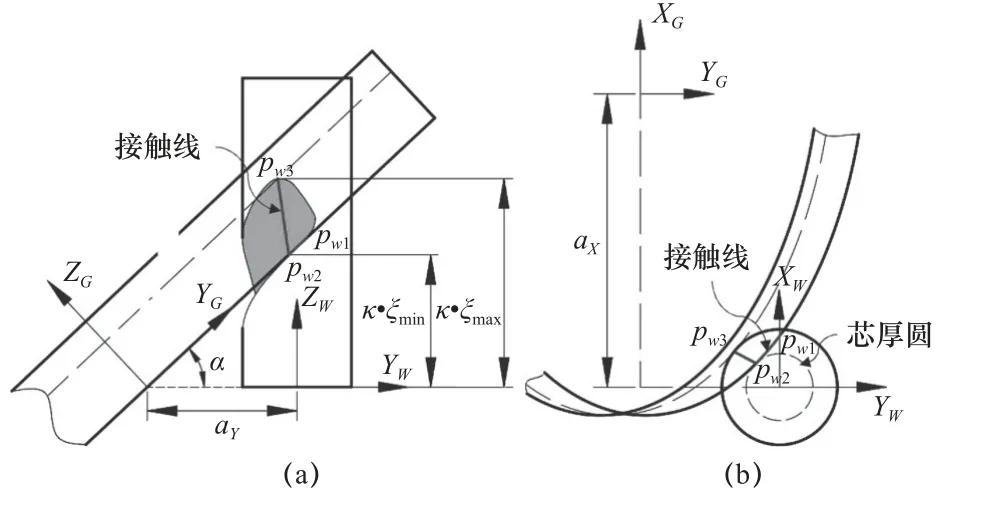
图4 螺旋槽曲面上接触线求解区间
定义刀具螺旋槽曲面上接触线的点为pwn,接触线最低点pw2为砂轮端面椭圆于芯厚圆相切点,接触线最高点pw1或pw3,其中pw1为砂轮端面圆与刀具棒料圆的交点,pw3为砂轮某个截面刀具棒料外圆柱面切点。因此在图4a 中,rc为芯厚半径,经过点(-rc,0)并平行于ZW轴的直线与砂轮端面的交点pk2一定略低于pw2,与砂轮的另一侧砂轮端面的交点pk3一定高于pw3,砂轮端面与刀具棒料右侧母线的交点pk1一定高于pw1。接触线求解区间预估如下:
式中:Hg为砂轮厚度。
将旋槽径向截形轮廓坐标点S(x(t),y(t))代入式(6),计算螺旋槽接触线旋转角度ξ(t),则螺旋槽曲面与磨损砂轮回转面的接触线pw(t)在砂轮坐标系下表示为
将接触线pw(t)绕砂轮轴线回转得到磨损砂轮回转面方程C(t,ψ),其在砂轮坐标系下可表达为:
2 磨损砂轮的磨削位姿约束函数关系
根据上一节计算得到的磨损砂轮轮廓,需要通过调整砂轮磨削位置和姿态,对所加工螺旋槽轮廓进行补偿从而持续保证螺旋槽的加工精度。基于此,首先基于磨损砂轮重新构建螺旋槽轮廓计算模型,然后根据螺旋槽结构参数几何定义建立磨损砂轮的位姿约束函数关系式。
2.1 基于磨损砂轮重构螺旋槽轮廓计算模型
为了与上一节中螺旋槽曲面上的接触线pw区别,本节计算的接触线为砂轮回转面上的接触线pg。在螺旋槽磨削过程中,砂轮接触线上点的法矢量N(t,ψ)与速度矢量V(t,ψ)相互垂直[3-4],如图5 所示。由于磨削过程中砂轮与刀具的位姿关系相对恒定,为了计算方便且不失通用性,本文仅计算砂轮在初始位姿时接触线上点的法矢量与速度矢量。
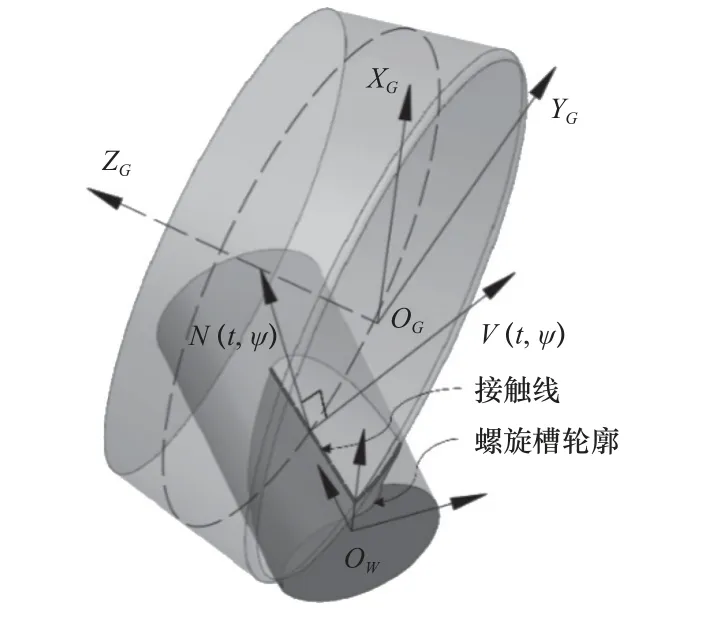
图5 螺旋槽径向截形轮廓形成原理图
(1)将砂轮回转面方程变换到刀具坐标系下进行描述。
对刀具坐标系下的砂轮回转面方程变量分别求偏导,并叉乘得到回转面点的法矢量N(t,ψ):
砂轮回转面上任意点的速度矢量V(t,ψ)为其运动变换矩阵Me(ξ)的导数:
(2)联立式(10)、式(12)和式(13),建立砂轮接触线的求解方程。
式中:B1=axcosα+κsinα,B2=(R(t)R′(t)-zL(t))sinα+ay,B3=(κcosα-axsinα)R′(t)。
将式(14)中sinψ与cosψ看成两个未知量,同时sin2ψ+cos2ψ=1,直线与圆的两个交点即为式(14)的解。由于螺旋槽磨削过程中砂轮只有靠近刀具的部分能参与磨削,接触线上所有点在坐标轴XG方向的坐标必定小于0(即cosψ> 0),因此接触线上点的回转角度ψ(t)可表达为
(3)将式(15)代入砂轮回转面方程式(11)计算出砂轮与工件的接触线C(t,ψ(t)),并将接触线通过运动变换矩阵变换到径向截面下,得到磨损砂轮磨削的螺旋槽轮廓方程。
2.2 螺旋槽轮廓与磨损砂轮的位姿约束

图6 螺旋槽径向截面下参数定义
(1)设螺旋槽轮廓线起点p1位于螺旋刃线上,则矢量P1与T1的夹角为前角。当T1×P1的ZW坐标为正时,前角为正,反之前角为负,螺旋槽前角关于砂轮位姿的函数fγ如下:
式中:tr(0,0,1)。
(2)设螺旋槽芯厚点为p2,螺旋槽轮廓与芯厚圆在点p2处相切,即矢量P2×T2=0。芯厚存在负芯厚情况,发生该类情况需要舍弃,如图7 所示,芯厚关于砂轮位姿的函数frc如下:
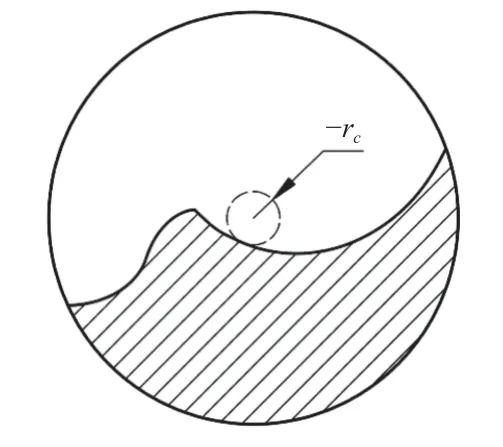
图7 负芯厚示意图
(3)设螺旋槽轮廓曲线终点为p3,则矢量P3与P1的夹角为槽宽。当P1·P3的ZW的坐标为正时,槽宽小于180°,反之槽宽大于180°,如图8 所示。槽宽关于砂轮位姿的函数fϕ如下:
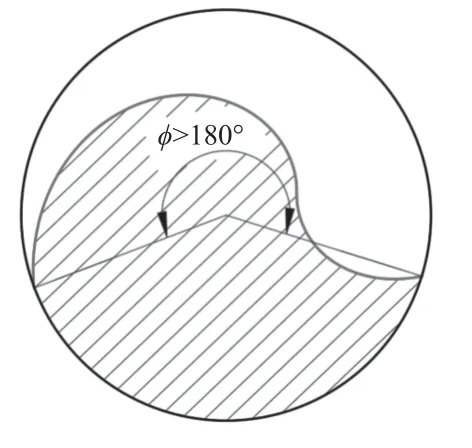
图8 槽宽ϕ>180°示意图
3 磨损砂轮的磨削位姿调整迭代计算
为了设计磨损砂轮位姿求解算法,首先根据式(17)~式(19)分别分析砂轮位姿中心距ax、偏移距ay、安装角α对螺旋槽结构参数的影响,如图9所示。可以看出,砂轮位姿VecX(ax,ay,α)每项参数都会影响到螺旋槽结构参数的变化,因而采取分而治之的迭代规则无法得到全局最优解。
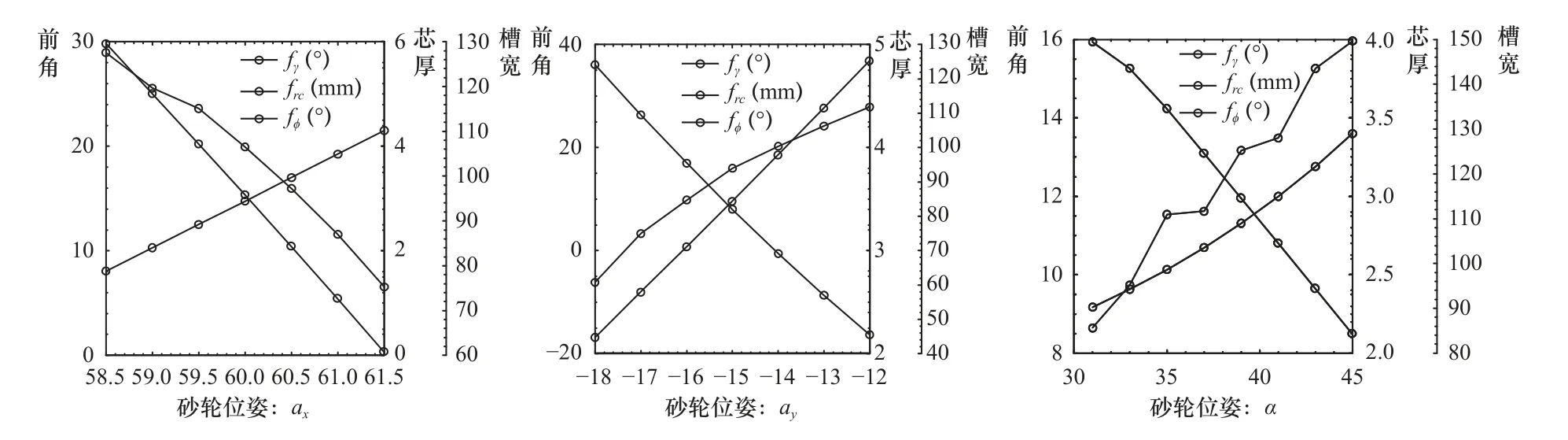
图9 砂轮位姿对螺旋槽结构参数的影响
因此,需要将砂轮位姿看成一个整体将非线性方程组求解问题转换成数学优化问题是一种高效处理方法。
式中:权重系数1≥ε1≥ε2≥ε3。
本文采用粒子群算法作为示例进行求解,其迭代规则见式(21),算法流程如图10 所示。
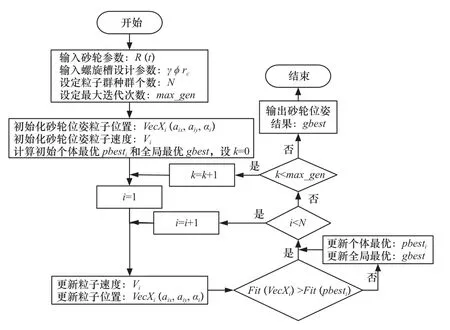
图10 磨削算法流程图
式中:ω为惯性权重,c1和c2为学习因子,r1和r2为[0,1]的随机数,pbesti为个体最优,gbest为全局最优。
值得注意的是,算法的初始砂轮位姿搜索空间估计对于求解稳定性至关重要。砂轮磨损会导致实际磨削的螺旋槽与设计相比,前角和槽宽参数变小,芯厚参数变大。由图9 的分析可知,砂轮位姿搜索空间应当减小中心距ax、增大偏移距ay。为了避免砂轮磨削式刃线发生干涉,砂轮安装角α的范围为[90-β,0)。
4 试验验证
4.1 螺旋槽设计及磨削工艺初始参数设置
为了验证本文提出算法的有效性,试验在某刀具企业的整体式立铣刀加工过程中进行。螺旋槽设计参数和加工所使用的砂轮几何参数见表1。螺旋槽磨削NC 代码由数控磨床配套软件生成,换算成砂轮安装位姿见表1。试验所使用的五轴数控工具磨床(JL-20155X)及砂轮(SDC120C100-C)如图11所示。
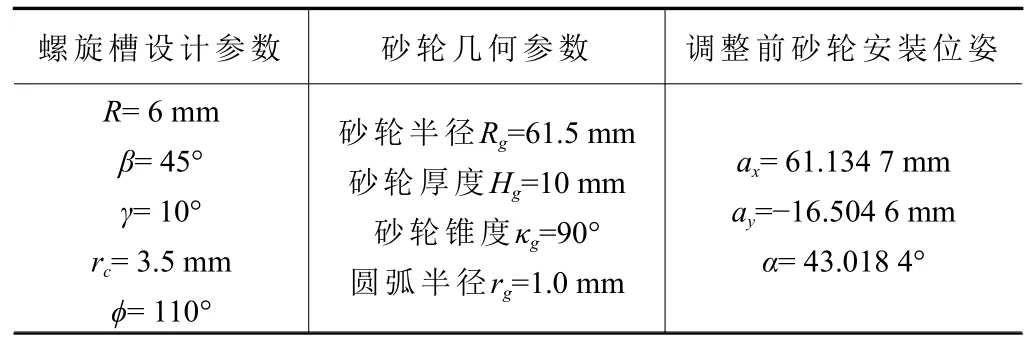
表1 螺旋槽设计和磨削工艺初始参数

图11 螺旋槽磨削所使用的机床与砂轮
4.2 不规则磨损砂轮轮廓的反求计算及误差分析
砂轮在完成若干次螺旋槽磨削之后,选用最近加工的一支刀具棒料,使用光学检测仪PG1000 对其螺旋槽端面轮廓进行测量,得到螺旋槽轮廓点坐标见表2。将轮廓点采用三次样条曲线插值拟合方法得到调整前加工的螺旋槽轮廓方程,与设计的螺旋槽轮廓对比如图12 所示。分析对比结果可知,砂轮由于磨损导致磨削加工的螺旋槽与设计要求相比有较大误差,前角误差为34.133%,芯厚误差为26.312 3%,槽宽误差为8.714 4%。其中螺旋槽前刀面的磨削量最大,磨削该处的砂轮磨损也最为严重,前角γ和芯厚rc误差均超过25%,已经完全不满足加工要求。
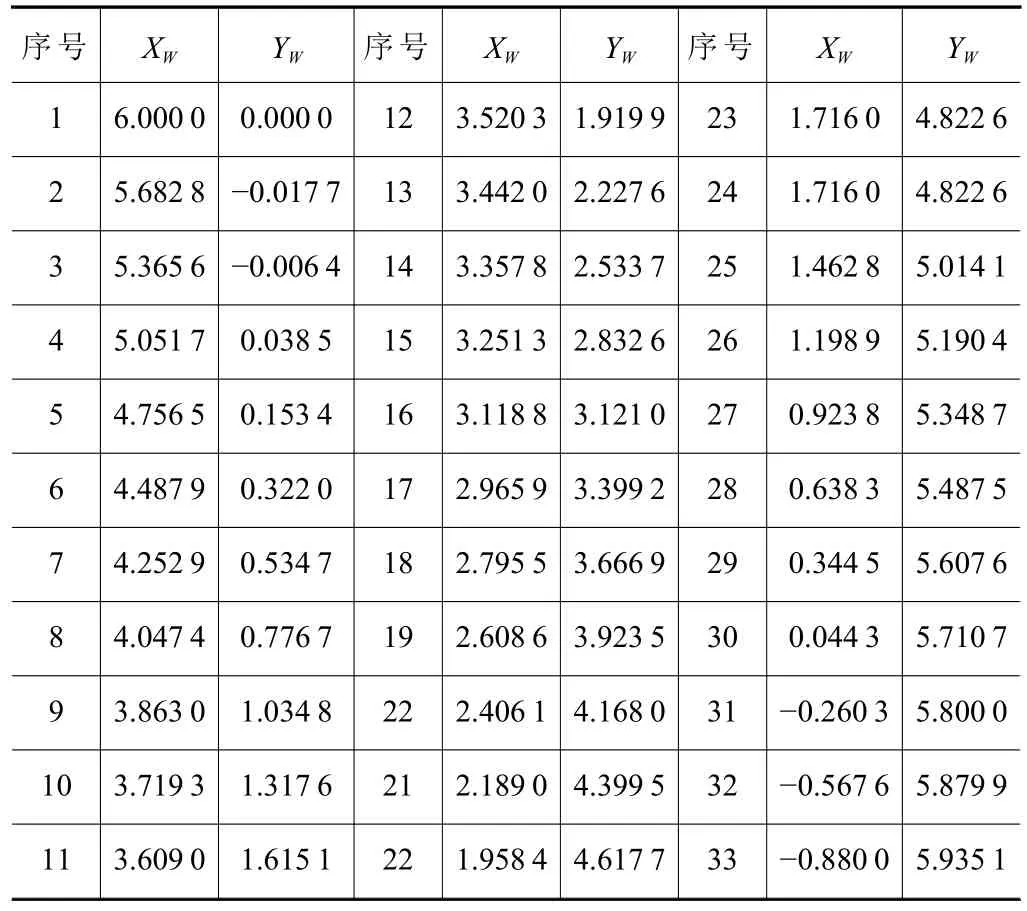
表2 磨损砂轮位姿调整前磨削的螺旋槽轮廓点坐标测量值

图12 调整前的螺旋轮廓磨削结果实测图
根据调整前加工的螺旋槽轮廓曲线,采用本文第1 章所提出的方法计算磨损砂轮轮廓(图13),得到砂轮轮廓点坐标见表3,磨损砂轮形状如图9所示。对比螺旋槽加工误差,砂轮越靠近端面部分磨损越严重,且磨损看轮廓弧线曲率也越来越大,呈现不规则磨损状态。
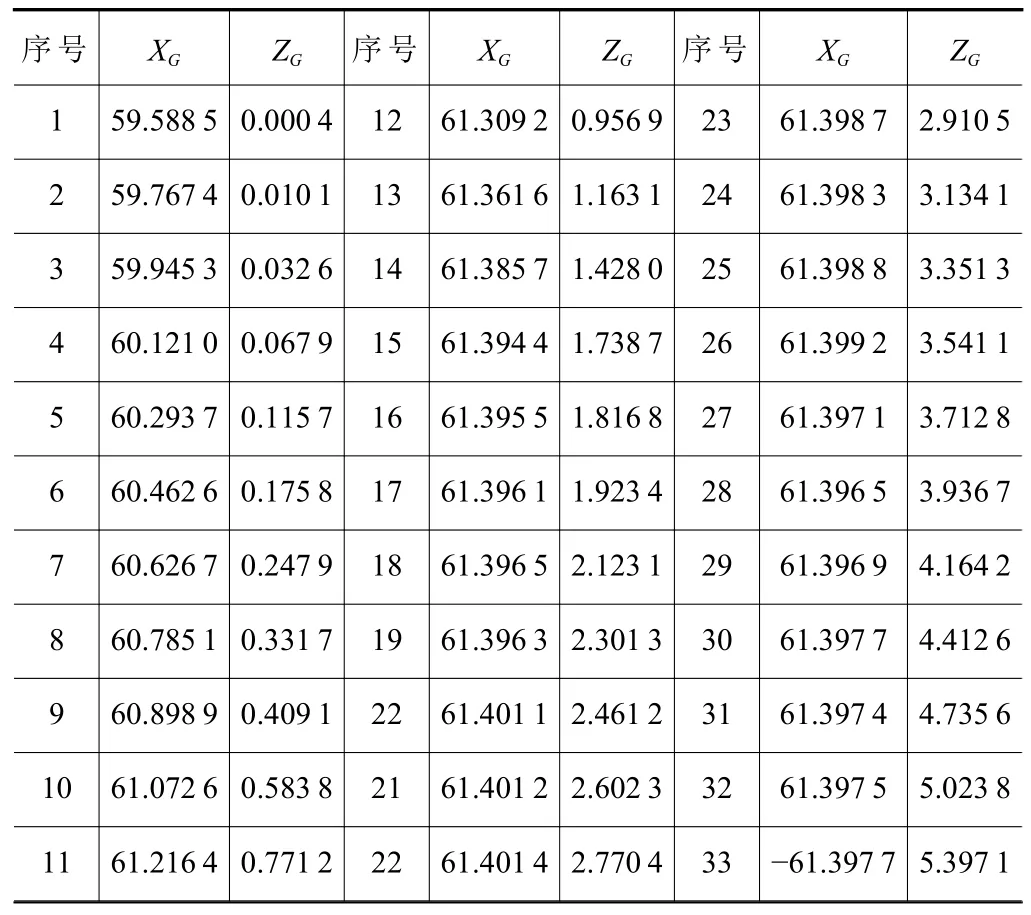
表3 反算得到的磨损砂轮轮廓点坐标值

图13 反算的磨损砂轮轮廓图
4.3 磨损砂轮的磨削位姿调整及结果分析
根据本文第3 章提出的磨损砂轮位姿优化算法,采用Visual Studio 2019 编写图7 所示的C++算法程序,算法参数设置、计算得到的砂轮磨削位姿见表4。将砂轮位姿生成砂轮磨削轨迹进行仿真加工,将砂轮磨削轨迹经后置处理生成机床加工NC 代码,对铣刀螺旋槽进行磨削加工,仿真加工与实际加工结果如图14 所示。分析加工结果可知,仿真加工的螺旋槽各参数误差均在0.01%以下,由于实际加中机床误差无法避免,实际加工的各项结构参数误差均在1%以下,满足加工需求。对比4.2 的加工结果可知,本文提出的磨损砂轮优化调整算法能有效解决砂轮加工过程中砂轮不断磨损导致加工精度不足的问题。

表4 算法参数设置

图14 调整后的螺旋槽截形仿真及实测图
5 结语
(1)针对螺旋槽磨削过程中砂轮不规则磨损导致螺旋槽加工精度降低的问题,提出了一种计算磨损砂轮轮廓以及位姿优化的算法。
(2)对砂轮和螺旋槽之间的接触线求解的数学原理进行了阐述,并通过砂轮的位姿对接触线的求解区间做出预估,确保磨损砂轮轮廓求解的正确性,结果表明所求解的砂轮轮廓与实际磨损砂轮轮廓基本一致。
(3)采用粒子群算法针对磨损砂轮重新进行位姿优化,通过三刃平头立铣刀进行磨削实际加工,最后对比了螺旋槽设计参数与实际加工的螺旋槽的参数的误差大小,实际加工误差均在2%以下,证明了该算法能够满足工程的需要。
