指向深度理解的概念教学路径建构

陶然

［摘 要］数学概念是数学体系的基石，促进学生对数学概念的深度理解是概念教学的应然追求。教学中，教师应引导学生通过类比归纳、实验观察以及矛盾辨析加深对数学概念的理解，进而使学生原有的数学认知结构得到整合与优化，从而提升学生的数学思维品质，发展学生的数学学科核心素养。

［关键词］数学概念；深度理解；初中数学

［中图分类号］    G633.6            ［文献标识码］    A          ［文章编号］    1674-6058（2023）27-0017-03

要学好数学，深度理解数学概念是前提。应试教育背景下，教师往往为了赶进度而采用填鸭式教学，学生只能机械模仿学习，对于数学概念的理解浮于表象，没有达到迁移性的深度理解。心理学家奥苏贝尔指出，真正的理解应把新知识归入原来的认知体系，在新旧知识间发生有意义的同化，这种同化不是任意的，而是一种合情合理的、自然而然的联系。笔者以为，要使学生深度理解数学概念，可引导学生通过类比迁移、实验观察、矛盾辨析等途径加深对数学概念的理解。下面是笔者的一些教学实践与思考，旨在探究基于深度理解的概念教学路径。

一、通过类比归纳，深度理解数学概念

根据来源不同，数学概念可分为两类：第一类是由现实中的事物或关系抽象而成的数学概念，如圆柱、圆锥、棱柱、棱锥、轴对称与轴对称图形等；第二类是从数学知识中抽象出来的数学概念，它是抽象思维的产物，如无理数、有理数、整式、一元一次方程、一元二次方程等。教师可根据数学概念的特征，设计学生熟悉的问题情境，引导学生运用已学知识回答问题，从结果中找到它们的共同特性，最后通过类比与归纳得到一般特征，形成数学概念。

［案例1］一元二次方程的概念教学片段。

教师：请同学们回忆一下，什么叫作一元一次方程？并举几个一元一次方程的例子。

学生1：只含有一个未知数，且未知数的次数是1的整式方程叫作一元一次方程，如[2x+6=11]；[x-1=3-x]；[2（x-2）=5-3（x-2）]等。

问题1：2022年是大丰收的一年。某村种的水稻2020年平均每公顷的产量是7200千克，2022年平均每公顷的产量是8400千克。若水稻平均每公顷的产量平均每年的增长率为[x]，则可列出方程：                     。

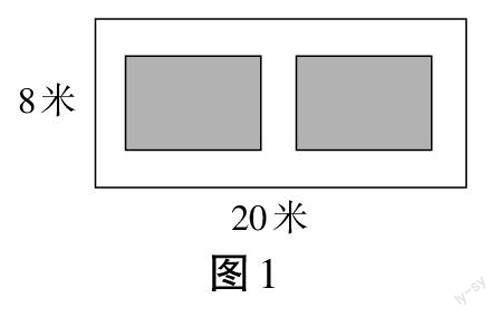
问题2：如图1，有一块长20米、宽8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56平方米，两块绿地之间及周边留有宽度相等的人行通道，那么人行通道的宽度是多少米？设人行通道的宽度为[x]，列方程得               。

学生2：问题1的方程为[7200（1+x）2=8400]；问题2的方程为[（20-3x）（8-2x）=56]。

教师：请同学们把方程整理一下，去括号，写成右边为0的形式。

学生3：第一个方程可整理为[6x2+12x-1=0]；第二个方程可整理为[3x2-32x+52=0]。

教师：这两个方程与前面学习的一元一次方程相同吗？如果不同，这样的方程应该叫作什么方程呢？为什么？

学生4：这两个方程并不是前面学习的一元一次方程，这两个方程应该叫作一元二次方程，因为未知数的最高次数是2。

教师：只含有一个未知数，且未知数的最高次数是2的方程就一定是一元二次方程吗？[1x+x2=1]是一元二次方程吗？为什么？从这里你得到什么启示？

学生5：方程[1x+x2=1]不是一元二次方程，因为方程中含有分式[1x]，这样的方程应称为分式方程。

学生6：判定一个方程是否是一元二次方程，还要看它是不是整式方程。

教师：也就是说，只含有一個未知数，且未知数的最高次数是2的整式方程叫作一元二次方程。

通过类比一元一次方程的概念构建一元二次方程的概念，使学生真正理解“一元一次方程”与“一元二次方程”定义的一致性。在“二元一次方程”概念的形成过程中，学生实现了深度学习。

二、通过实验观察，深度理解数学概念

实验是科学研究的重要方法之一，它是指根据一定的研究目标，利用现有的工具，如刻度尺、量角器、计算器等，对客观事物进行控制和模拟，最大限度地排除次要因素的影响，凸显主要因素，从而获得经验性素材，达到认识自然现象和规律的目的。观察是指人们按照客观事物本身存在的自然状态，发现和确定客观事物的性质与关系，进而收获经验性素材的方法。实验观察是促进学生深度理解数学概念的有利抓手，可使学生在直观表象与动态演绎中实现对数学概念的深度理解。

［案例2］“圆与圆的位置关系”中的概念教学片段。

问题：请同学们观察图片，奥运会上的五环标志、自行车的两个车轮、五个齿轮组成的传动装置、飞镖靶等，它们中圆与圆之间的关系有何不同？

学生1：在奥运会的五环标志中，上面的三个圆之间没有公共点，下面的两个圆之间也没有公共点，但是上面的圆与下面的圆分别各有两个公共点。

学生2：自行车的两个车轮之间没有公共点。

学生3：五个齿轮组成的传动装置中，里面的三个小圆与外面的大圆只有一个公共点，三个小圆与中间的圆也只有一个公共点。

学生4：飞镖靶的几个圆之间没有公共点。

教师：那么两个圆之间有哪些位置关系呢？我手中有一大一小两个圆环，请一位同学帮忙在黑板上将一个圆环固定，我将另一个圆环由近及远地向固定的圆环靠近，注意观察这两个圆公共点个数的变化。

教师：通过刚才的实验与观察，你看到两个圆的公共点个数存在几种情况？圆与圆之间的位置关系可分为几种类型？分类的标准是什么？

学生5：两个圆的公共点个数存在没有公共点、只有一个公共点、有两个公共点三种情况。因此，圆与圆之间的位置关系可分为三种类型，分类的标准是公共点的个数。

教师：如图3所示，第一个图与第五个图中，虽然两个圆都没有公共点，但是它们的位置关系一样吗？第二个图与第四个图中，虽然两个圆都只有一个公共点，但是它们的位置关系一样吗？它们有什么不同？

学生6：第一个图与第五个图中两个圆虽然都没有公共点，但是它们的位置关系不一样。第一个图中小圆在大圆的内部，第五个图中小圆在大圆的外部。

学生7：第二个图与第四个图中两个圆虽然都只有一个公共点，但是第二个图中小圆在大圆的内部，第四个图中小圆在大圆的外部。

教师：由此看来圆与圆的位置关系应分为五种，这五种位置关系依次叫作内含、内切、相交、外切与外离。除了根据公共点个数判定两圆的位置关系，还有没有其他的方法可以判定两圆的位置关系呢？

学生8：还可以用两圆半径与两圆心之间的距离来判定。用[d]表示两圆心之间的距离，用[R]、[r]分别表示两圆半径，当两圆内含时，[d<R-r]；当两圆内切时，[d=R-r]；当两圆相交时，[R-r<d<R+r]；当两圆外切时，[d=R+r]；当两圆外离时，[d>R+r]。

在教学中，学生通过实验和观察，归纳出圆与圆的位置关系及其蕴含的规律，并形成了对圆与圆内含、内切、相交、外切、外离五种概念的深度理解。

［案例3］“图形变换”中的概念教学片段。

教师：下面请同学们欣赏几幅美丽的图片。（教师展示几幅轴对称图形，包括北京天安门、蝴蝶、人体、五角星、剪纸等）请同学们认真观察这些图片，说说它们有什么共同特征。

学生1：北京天安门、蝴蝶、人体、五角星、剪纸等，都关于中间的一条直线左右对称。

教師：下面请同学们沿着你认为的中间的直线折叠图片，看看左右两边的图案是否重合。

（学生纷纷动起手来，把这些图片沿对称轴折叠，发现折叠后直线两旁的部分能互相重合。）

教师：我们把这样的图形称为轴对称图形。请同学们总结一下，一个什么样的图形叫作轴对称图形呢？

学生2：一个图形沿着一条直线折叠，如果直线两旁的部分能够互相重合，那么这个图形叫作轴对称图形，这条直线叫作对称轴。

活动1：把自己的双手放在同一高度，掌心相对，然后合掌，你会发现什么？

学生3：我发现两只手能互相重合。

活动2：在空白纸上滴一滴墨水，然后沿墨水外的一条直线折叠纸张，使墨水印在直线的另一侧，打开纸后你会发现什么？

学生4：打开纸后我发现折线两侧的墨迹一模一样，能够互相重合。

教师：当两个图形沿一条直线折叠后能够互相重合，这样的两个图形，我们称之为成轴对称。这条直线就是对称轴。那么成轴对称与轴对称图形有何区别与联系？

学生5：轴对称图形是指一个图形，而成轴对称是指两个图形，它们都有对称轴，沿对称轴折叠后都能重合。

学生6：如果把轴对称的两个图形看成一个图形，那么成轴对称就变成了轴对称图形。

在上面轴对称图形与成轴对称的概念建构过程中，学生依靠对轴对称图形的观察和动手操作获得了轴对称的本质特征，进而形成了轴对称的概念。

三、通过矛盾辨析，深度理解数学概念

数学中有许多的“规定”，它们包括基本的数学定义、特定的数学符号、特定的书写模式等。在中学数学教材中，这样的规定有很多。为什么要做出这样的规定呢？作为数学教师，一方面自己要明白其所以然，另一方面还要让学生在矛盾辨析中体会这些规定是正确的、合理的，感知这些规定背后的数学道理、内含的数学智慧，从而深度理解数学概念。

［案例4］单项式的补充规定教学片段。

教师：通过前面的学习，同学们已经知道表示数字或字母乘积的式子叫作单项式，并且规定：单独的一个数字或一个字母也是单项式。那么，同学们知道为什么要做出这样的规定吗？

（大部分学生不知如何表达或者不能清楚地表达）

教师：“[1×50]”是不是单项式？为什么？

学生1：单项式指的是表示数字或字母乘积的式子。“[1×50]”表示数字“1”和数字“50”的乘积，因此“[1×50]”是单项式。

教师：“50”是单项式吗？

学生2： “50”不是数字或字母的乘积，因此，它不是单项式。

学生3：学生2说的既有对的成分又有不对的成分。从形式上看，虽然“50”不是数学或字母的乘积，但是“50”可以看作“[1×50]”的简写形式，而“[1×50]”是单项式，所以“50”也是单项式。

教师：看来同学们对于“50”是不是单项式产生了分歧。那么，如何才能解决这一分歧呢？这时，对单项式做出补充规定就显得非常必要。当我们规定“单独的一个字母或数字也是单项式”时，这一矛盾就顺理成章地解决了。

围绕单项式的内涵，教师巧妙捕捉学生的认知困惑和思维冲突，引导学生认识到单项式内涵补充规定的必要性。在单项式概念教学中，教师引导学生在矛盾中辨析，体验单项式概念的建构过程，使学生触摸到概念的本质，加深对数学的概念认识。

总之，数学概念是数学体系的基石，促进学生深度理解概念是概念教学的应然要求，也是落实数学学科核心素养的必然追求。教学中，教师可引导学生通过类比归纳、实验观察、矛盾辨析，深度理解概念，进而使学生原有的数学认知结构得到整合与优化，从而提升学生的数学思维品质，发展学生的数学学科核心素养。

（责任编辑    罗 艳）