运用RJMCMC 方法对上证指数连涨连跌收益率的Bayes 分析
2023-12-09程慧慧许淑月
程慧慧,许淑月
(华北水利水电大学数学与统计学院,河南 郑州 452370)
变点是指观测序列值在某一个位置或时间点发生了分布或者数字特征的突然变化,这个发生突变的位置或时间点就被称为变点.不考虑可能的变点就进行统计分析很可能会得到具有误导性的结果,因此关于变点问题的研究在金融、医学、气象学等方面有着广泛的应用价值.变点问题的研究始于Page[1]在1954 年发表的一篇关于连续抽样检验的文章,人们通过检测产品质量是否超过控制范围来判断产品质量是否发生显著波动,当产品质量超过控制范围就认为发生质变,质变的时刻就称为变点。随后变点问题受到了很多学者的重视并在理论[2-3]和应用[4-5]方面有了快速发展,处理变点问题的方法[6-10]也得到了进一步的完善.陈希孺等[6]利用局部法研究了变点问题;James 等[7]使用似然比方法检验多元正态分布中变点是否存在;Chemoff 等[8]应用贝叶斯(Bayes)方法检验正态分布中变点是否存在;李拂晓等[9]使用二元分割方法来检验多元Logistic 回归模型中存在的变点;陈睿轩等[10]利用非参数极大似然方法来估计金融时间序列中的变点.马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法是一种重要的贝叶斯计算方法,可将贝叶斯统计中复杂的计算简单化,在变点个数已知情形下,使用MCMC 方法可使变点检测变得更加简便.张晗等[11]在艾拉姆咖分布单变点模型中运用MCMC 方法得到了变点位置的有效估计;石凯等[12]采用MCMC 方法为多维混合分布数据的参数估计和识别提供了一种有效的解决途径;胡红波[13]将MCMC 方法运用到不确定评估的测量中,并介绍了关于指数分布的采样实例.1995 年Green[14]提出了可逆跳跃马尔可夫链蒙特卡洛(Reversible Jump MCMC,RJMCMC)方法,该方法实现了抽样过程在不同维数的参数子空间之间跳跃,十分适用于变点个数未知情形下的变点检测.Zhao 等[15]在层次贝叶斯框架下利用RJMCMC 算法识别极端事件序列中的多个突变状态,石永亮[16]利用RJMCMC 算法对线性回归模型的异常点进行识别,范元静[17]利用RJMCMC 算法确定泊松分布参数多变点模型中变点的个数并得到了参数估计.
股票收益率的波动一定程度上反映了股票的内在规律[18-20].通常股票收益率会受一些重大事件或政策的影响,由此产生一系列异常点,即变点.由雷鸣等[21]的研究可知,上证指数的连涨连跌收益率都服从伽马分布.关于伽马分布参数变点的研究,已有一些结果,如文献[22-26]讨论了典型的伽马分布序列中的单变点问题,Hsu[26]讨论了在伽马分布的形状参数已知时,检测伽马随机变量序列中尺度参数偏移的方法,并将其应用于股票市场收益率和交通流的分析中.但有关伽马分布双参数的多变点的研究还是比较少.2017 年胡俊迎[27]在变点模型中假设形状参数不发生变化,利用RJMCMC 算法对2005 年6 月至2015 年5 月的上证指数进行了研究,但是这样可能会忽略股市大势的影响.因此本文考虑在不限于形状参数不发生变化的情形下,建立伽马分布双参数的多变点模型,利用RJMCMC 方法确定模型的变点个数并得到变点位置的估计,最后将该方法应用到对上证指数连涨连跌数据序列的分析中.
1 连涨连跌收益率的理论分布与检验
本文研究了从2016 年5 月3 日至2022 年5 月20 日的上证股指,采用对数收益率作为每日收益率Rt,即Rt=lnPt-lnPt-1,其中Pt为每日收盘价.雷鸣等[21]由每日收益率Rt得到了连涨连跌的收益率,也就是统计每次股指开始上涨至上涨结束时收益率的和(连涨收益率),以及股指开始下跌至下跌结束时收益率的和(连跌收益率).他们还把生存分析引入到对股指的研究中,将连涨收益率和连跌收益率看作是两个不同的生存过程,这样连续涨跌的收益率就可被视为每次涨跌的寿命.由此,本文得到连涨连跌数据序列,见表1 和图1.
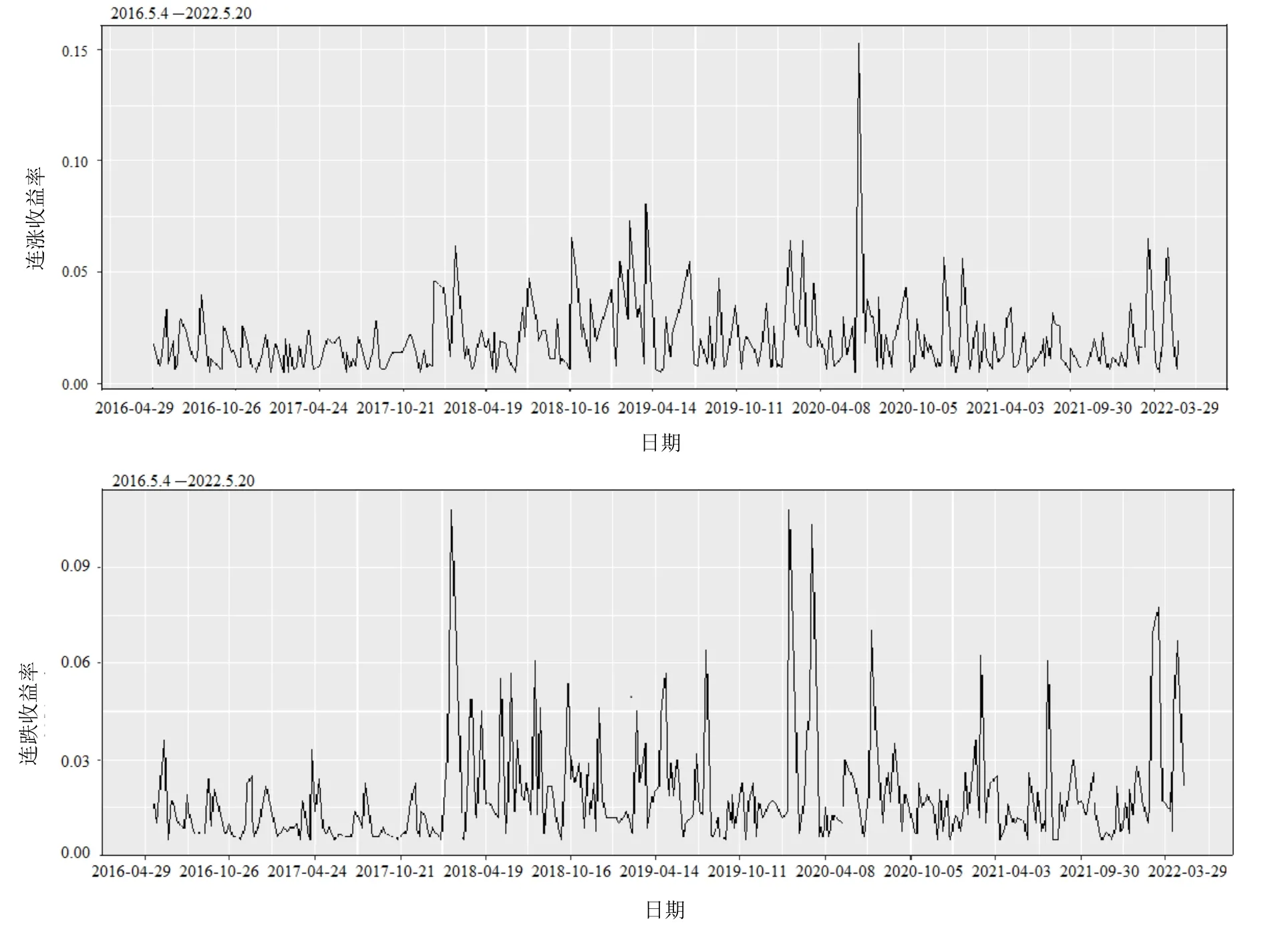
图1 上证指数连涨连跌收益率数据序列

表1 2016 年5 月3 日至2022 年5 月20 日上证指数连涨连跌收益率
谭长春等[22]研究发现,伽马分布可以很好地拟合连涨连跌收益率分布.设Y总体服从伽马分布,其概率密度函数为:
2 基于RJMCMC 下的伽马分布双参数的变点研究
2.1 建立伽马分布双参数的变点模型
为了方便,规定c0= 0,ck+1=n,其中,变点个数k以及变点位置c1,c2, … ,ck都是未知的,那么关于伽马分布双参数多变点模型,需要估计的参数有3(k+1) 个,分别是变点个数k,变点位置c1,c2,… ,ck,形状参数v1,v2,…,vk+1和尺度参数λ1,λ2, …,λk+1.
2.2 RJMCMC 方法介绍
贝叶斯统计学是基于总体信息、样本信息、先验信息进行的统计推断.设参数θ的先验信息分布为π( )θ,随机变量θ给定值时,总体的条件概率函数为p(x| )θ.样本X和参数θ的联合分布为h(X,θ)=p(X|θ)π(θ),利用贝叶斯公式
对参数θ进行统计推断.(2)式中m(X) 是样本X的边际密度函数,m(X) 不含关于θ的任何信息.本文数据序列的参数θ={k,c1,c2, …,ck,v1,v2, …,vk+1,λ1,λ2, …,λk+1}.
在实际问题中,上述后验密度分布(2)通常是比较复杂的未知形式,RJMCMC 方法作为一种重要的贝叶斯方法可以很好地解决这一难题,它以目标后验分布作为平稳分布的马尔可夫链生成随机数,代替从后验分布中直接抽取样本.
基于RJMCMC 下的伽马分布参数的变点分析,需要确定选取各参数的先验分布.可考虑各参数的先验分布如下.
1)变点个数k服从截断的泊松分布为标准化常数,kmax,α为给定的超参数.
2)从离散的均匀分布{0,1,2,3, …,n}上产生2k+ 1个顺序统计量,c1,c2,… ,ck作为其中的偶数阶统计量,其中0 3)取形状参数 {v1,v2,… ,vk+1}独立同分布于形状参数a和尺度参数b的Gamma 分布且均与变点位置相互独立,则vj~Gamma(a,b),j=1,2, …,k+1. 4)取尺度参数{λ1,λ2, …,λk+1}独立同分布于形状参数c和尺度参数d的Gamma 分布且均与变点位置相互独立,则λj~Gamma(c,d),j=1,2, …,k+1. 由贝叶斯分层理论,可得所有未知参数的联合先验分布: 再结合总体信息、样本信息得到参数后验分布的核密度函数: 接下来设计下面的移动类型来改变马尔可夫链的状态{k,c1…ck,v1…v k+1,λ1…λk+1}. (a)任意改变一个形状参数值; (b)任意改变一个尺度参数值; (c)任意改变一个变点的位置; (d)在{1,2, …,n}{c1,c1, …,ck}上任意选择新增加一个; (e)在 {c1,c1, …,ck}中任意选择减少一个. 需要得到每种移动下的接受概率. 若m=(a),假定vj被选择,新的形状参数满足=v j×eu且u是一个随机样本服从区间为[-0.5,0.5]的均匀分布.为了计算简便,选取的建议分布为q(vj,)=,则此种移动下的接受概率Pallow=min{1,A1},这里 同理,若m=(b),Pallow=min{1,A2},这里 若m=(c),从c1,c2, …,ck中任意选择cj发生改变,新的变点位置为.选cj-1+ 1,cj-1+2, …,cj+1-1上的离散均匀分布为建议分布经计算,可得接受概率Pallow=min{1,A3},这里,当 对于m=(d),假设在区间(c j-1,cj)上增加一个变点c*,则在区间(c j-1,c*)和(c*,cj)上会产生新的参数()和(),且vj在和之间,其关系用权重方式表示为: 经计算,似然比可直接表示为 先验比为 因此随机增加一个新变点c*的接受概率为Pallow=min{1,A4},这里 其中l.r.、p.r.、pro.r.、Jacobian 分别表示似然比、先验比、建议比、雅可比行列式. 针对m=(e),假设随机选择被减去的变点为cj,则区间(c j-1,c j,cj+1)变为(c j-1,cj+1).假设(v j′ ,λj′ ),(vj+1′,λj+1′ )为区间(c j-1,c j,cj+1)上的旧参数,(v j,λj)为区间(c j-1,cj+1)上的新参数,同理可得,随机减少变点cj的可接受概率为Pallow=min{1,A5},这里 随机生成含有400 个数据的Gamma 分布序列,分为3段,1―100,101―200,201―400,数据分别服从Gamma(1,1),Gamma(2,8),Gamma(5,15).3 段数据的参数不一致,可见存在2 个变点,分别在100 处和200 处.400 个随机数据模拟图如图2(a)所示.设定参数的初始值k= 3,c1=20,c2=50,c3=200,超参数kmax= 10,α= 5,a=25/4,b=5/4,c= 3,d= 1.迭代10 000 次算法,去掉前7 000 次,用后3 000次的结果来估计变点个数的后验概率,得出的变点个数估计如图2(b)所示. 图2 变点在(100, 200)的Gamma 分布数据模拟图及变点个数估计直方图 由图2(b)可知,变点个数为2 的后验概率最大,因此确定400 个Gamma 分布序列的变点个数为2.在变点个数的基础上进一步利用MCMC 方法估计变点位置参数和Gamma 分布参数.通过R 软件实现模拟,在模拟过程中进行40 000 次迭代抽样.为保证参数的收敛性,舍弃前20 000次抽样,根据后20 000 次结果进行统计分析.形状参数、尺度参数和位置参数的后验密度估计如图3 和图4 所示.由图3(a)可知,形状参数的后验密度分布有3 个峰,分别在1、2、5 附近;由图3(b)可知,尺度参数的后验密度分布有3 个峰,分别在1、8、15 附近.由图4 可知,变点位置的后验密度分布有2 个峰,分别在100、200 附近.以上数据与模拟的真实变点位置及所服从的Gamma 分布参数相符,这说明了算法对Gamma 分布双参数多变点检测的有效性. 图3 形状参数和尺度参数的后验密度分布 图4 两变点位置的后验密度分布及迭代图 通过对上证指数的连涨连跌收益率进行KS 检验,发现其分布仍服从伽马分布,则在此基础上运用上述的RJMCMC 变点理论方法对服从伽马分布的数据序列作参数变点检验. 由上述RJMCMC 方法分别对连涨连跌收益率先进行变点个数的确定,然后进一步利用MCMC 方法得到变点位置参数和分布参数的后验估计.同样地先将方法进行10 000 次迭代去掉前7 000 次,确定变点个数,在此基础上再进行40 000 次迭代抽样并舍弃前20 000 次,根据后20 000 次抽样结果进行统计分析,结果如图5(a)、图6(a)所示.由图5 可看出,连涨数据序列存在2 个变点,变点位置分别在81,191(对应日期分别为2018 年3 月8 日,2020 年7 月31日);由图6 可看出,连跌数据序列存在3 个变点,变点位置分别在70,190,264(对应日期分别为2017 年12 月14 日,2020 年8 月2 日,2022 年1 月25 日). 图5 连涨收益率数据序列的参数变点检验图 图6 连跌收益率数据序列的参数变点检验图 从上述的实证结果来看,连涨收益率与连跌收益率数据的前两个变点与实际情况是基本吻合的,也就是说股市在2018 年初以及2020 年下半年不论涨跌都发生了较大幅度的震荡.首先,2016年到2017 年年末这段时间内没有变点,刚好对应着股市长达近两年的慢牛行情.其次,连涨的第一个变点在2018 年3 月8 日附近,连跌的第一个变点在2017 年年末,都刚好处于2018 年中美贸易战爆发的时间端口.连涨和连跌的第二个变点集中在2020 年8 月初附近.2019 年末国内爆发新冠疫情,随后疫情肆虐全球,全球经济不断下行.在2020 年下半年,随着我国疫情逐渐好转,民众的恐慌心理得以缓解,我国股市也开始一路小涨,呈现稳中向好的趋势.第二个变点时间也都正好与2020 年8 月中国首个新冠疫苗被授予专利权以及数字人民币试点开始实施等的时间点相对应.最后关于连跌数据序列最后一个变点2022 年1 月25 日,应该与2022 年美联储的多次加息、疫情的不断反复、俄乌冲突的不断升级以及1 月全球股市大跌相关. 本文针对上证指数收益率数据,基于伽马分布双参数多变点模型,首先通过建立RJMCMC方法来得到数据序列中的变点个数及变点位置的后验估计,然后对上证指数的连涨连跌收益率进行实证分析,判断上证指数收益率是否存在变点,确定变点的个数及位置,进一步分析由此给股市带来的变化.分析结果证明了该方法的有效性,也说明了金融序列中变点发生的时间与国际经济环境、国家宏观经济、国家重大政策等存在必然的联系.变点的产生意味着股票市场不正常的剧烈波动,蕴藏着股票市场的未来趋势.因此,基于RJMCMC 算法对金融序列中变点问题进行研究,有利于分析股市变化,可以为投资者提供一定的理论依据,对合理度量市场风险、进行风险管理有一定的理论和现实意义.2.3 数值模拟
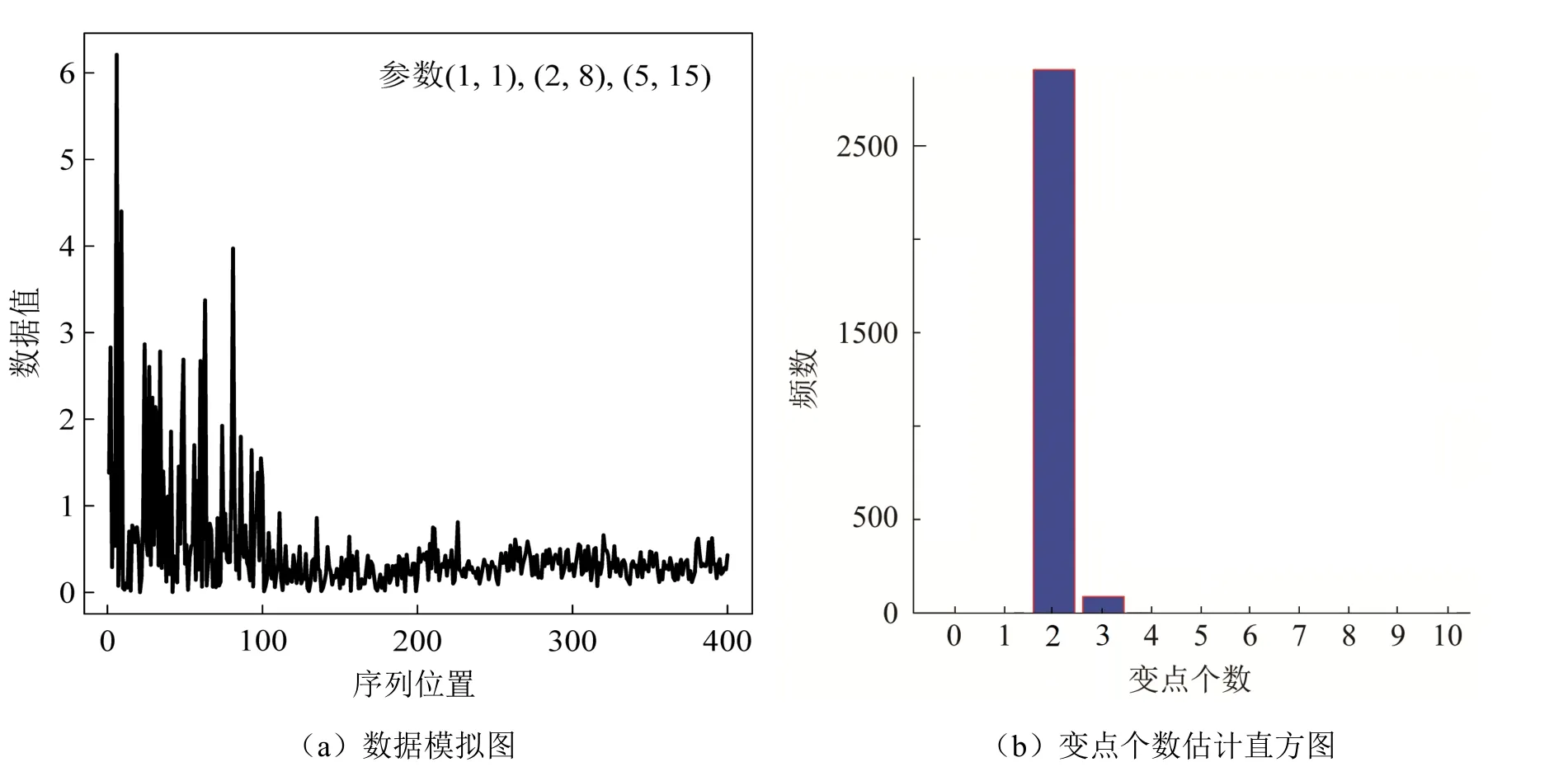
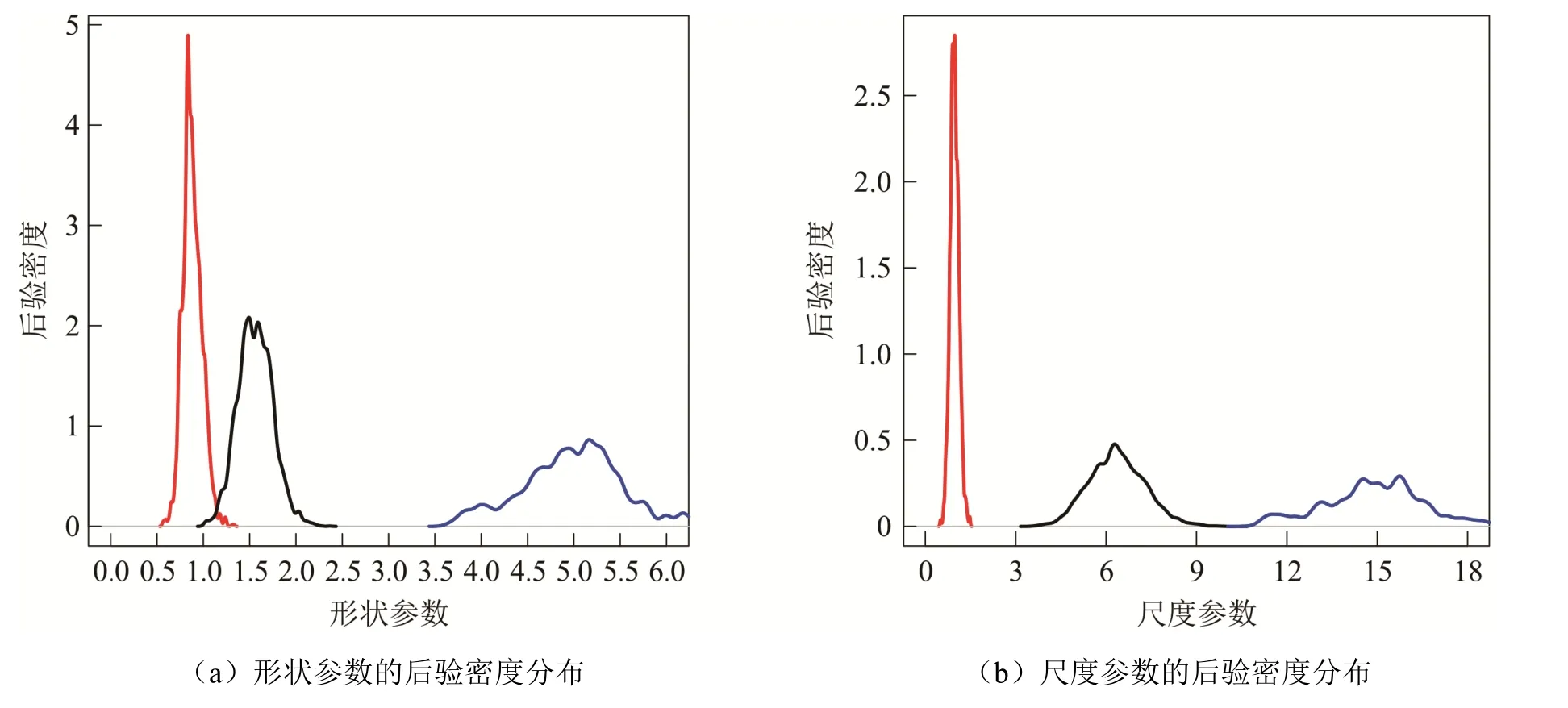
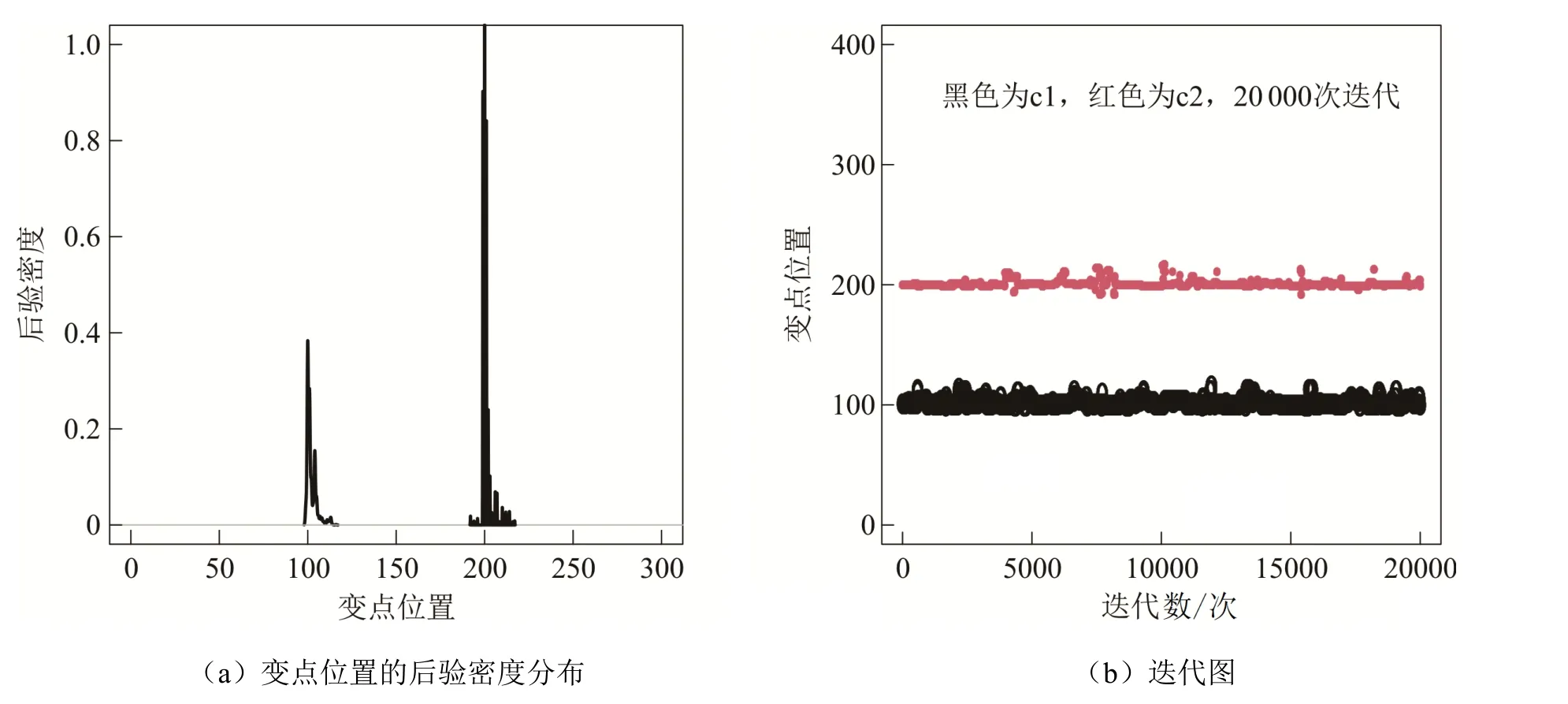
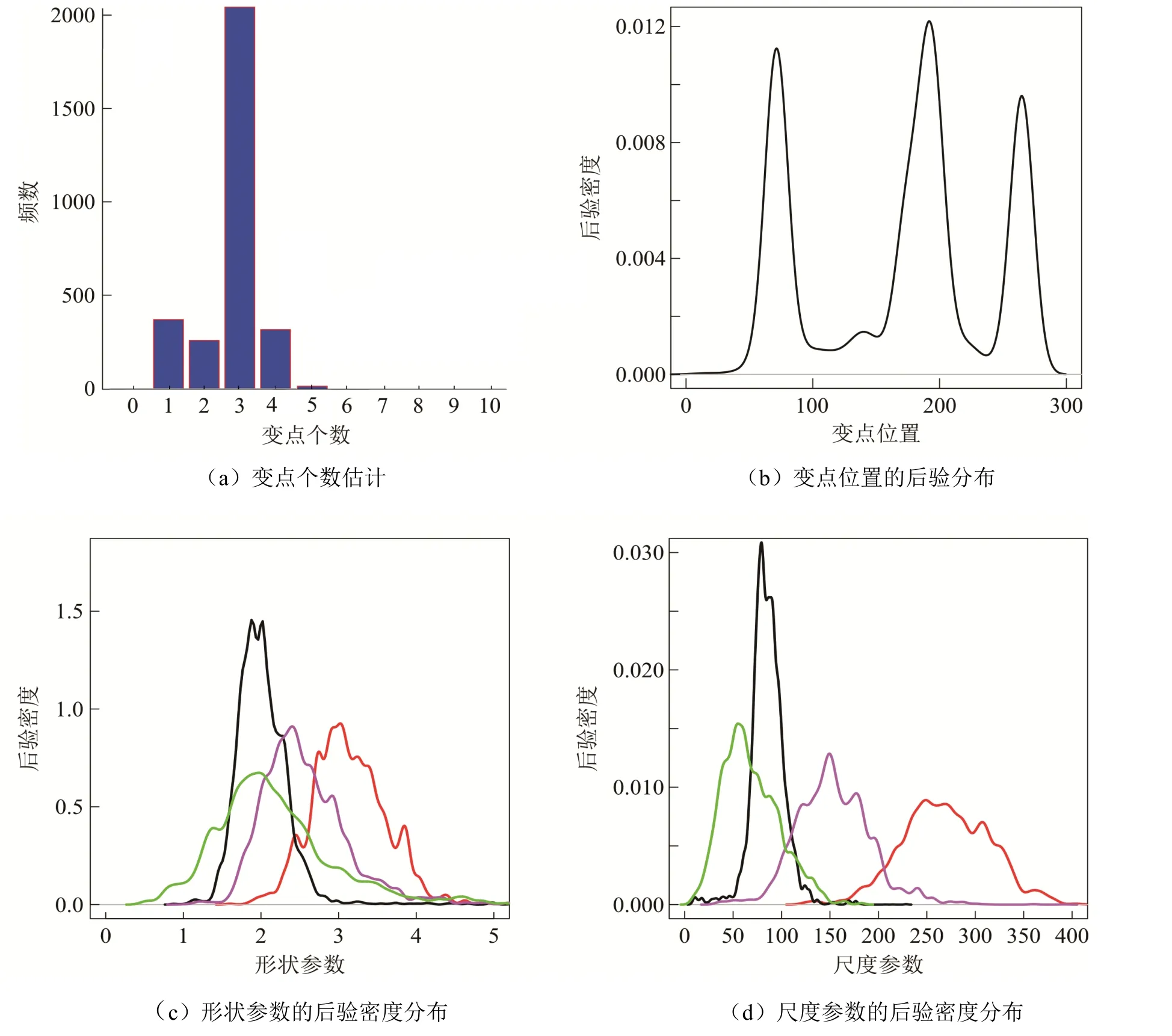
3 实证检验与分析

4 结 语
