焊趾半径对疲劳短裂纹演化行为的影响

钟广生，魏国前,,3，闫梦煜，冯梓彬

(1.武汉科技大学,冶金装备及其控制教育部重点实验室,武汉,430081；2.武汉科技大学,机械传动与制造工程湖北省重点实验室,武汉,430081；3.武汉科技大学,精密制造研究院,武汉,430081)

0 序言

焊接是常用的连接方式，广泛应用于海洋平台、桥梁结构、航空航天等钢结构中.统计数据表明，疲劳破坏是焊接结构的主要失效形式[1].而焊缝由于局部形貌、材料组织及应力状态复杂，易发生应力集中效应，是焊接结构的薄弱部位.其中，焊趾是疲劳裂纹最有可能萌生的区域.针对焊趾部位的长裂纹阶段，疲劳性能评定方法已趋于成熟，主要有名义应力法、结构应力法、缺口应力法和基于断裂力学的方法.然而，上述方法均无法评定疲劳短裂纹阶段疲劳性能，无法满足工程机械的关键部件耐久性要求.因此，针对宏观结构的疲劳短裂纹演化行为研究显得尤为迫切而重要.

近年来，一些学者通过晶体塑性有限元方法来研究疲劳短裂纹演化行为.成立夫等人[2]仿真了焊趾局部的疲劳短裂纹行为，发现疲劳寿命受到晶粒尺寸和晶粒取向的共同影响，但没有考虑焊趾局部的几何因素与材料的循环塑性行为.邓彩艳等人[3]耦合位错模型和有限元方法，获得了与试验数据接近的焊接接头各区域疲劳短裂纹寿命.Zhang 等人[4]以单个滑移系的累积剪切应变为驱动，成功模拟了短裂纹的曲折扩展与扩展速率的波动变化.一些学者通过跨尺度仿真技术将晶体塑性有限元推向工程应用，针对宏观结构研究疲劳短裂纹演化行为.Mlikota 等人[5]基于Tanaka-Mura 方程探究了宏观构件的过载对微观结构模型短裂纹阶段行为的影响，发现过载加速了短裂纹扩展.张凭等人[6]提出了CP-XFEM 的多晶短裂纹模拟方法，预测了发动机涡轮盘危险截面处的短裂纹扩展路径及速率.另外，近年来发展了多种焊接件疲劳延寿技术[7]，包括焊趾打磨技术、激光重熔技术及TIG 熔修技术等，通过修饰焊趾几何延长疲劳寿命.然而，针对焊趾半径对疲劳短裂纹演化影响的研究却鲜有报道.

针对上述现状，文中综合泰森多边形法和子模型技术，构建了十字形焊接接头中焊趾半径处的RVE 子模型，采用基于FIP(fatigue indicator parameter)参量的微观结构敏感的疲劳短裂纹扩展模型，计算了基于滑移带平均的FIP及裂纹寿命，宏观-微观跨尺度地模拟了微观短裂纹成核和扩展行为，研究了焊趾半径对疲劳短裂纹演化行为的影响.

1 理论基础

1.1 基于FIP 的短裂纹扩展模型

Manonukul 等人[8]为研究材料微观结构的疲劳短裂纹演化，首次利用晶体塑性有限元计算了疲劳指标参量FIP.Mcdowell[9]认为裂纹萌生机理与微观结构的不可逆滑移行为有关，并基于Fatemi-Socie 准则修正了FIP.修正的FIP适合表征晶粒层面的疲劳短裂纹演化，即

基于滑移带平均的FIP简化了裂纹逐单元扩展中FIP的变化过程，驱动裂纹逐晶粒地扩展.这种简化策略相比裂纹逐单元扩展能够以更高的计算效率达到相近的预测结果.具体来说，代表性体积单元RVE 中晶粒划分成与主滑移面平行的驻留滑移带(PSB,persistent slip band)，各网格单元计算得到的FIP参量在PSBs 上取平均值，平均FIP表达式为

式中：FIP0是 晶粒开裂前的FIP值，Dst是晶粒中滑移带的长度；RGB和m表征晶界对PSBs 滑移的阻力.

裂纹成核(nucleation,nuc)寿命定义为RVE 中首个晶粒开裂所需的最小循环次数.由于裂纹成核机理复杂，成核寿命可用半经验公式计算，即

式中：Dst是 当前晶粒的滑移带长度；Dnd是相邻晶粒中与之交叉的滑移带的长度；ω是与相邻晶粒的取向差因子，取向差角度大于20°时取0.

基于FIP参量，微观短裂纹(MSC,microstructurally small crack)阶段PSBs 扩展速率方程为

式中：ϕ是度量裂纹尖端塑性区的不可逆性的参量(通常为0.01～ 0.1)；ΔCTDth是发生位错所需的最小循环次数的阈值；A是 与有关的比例常数是晶粒参考长度，一般取平均晶粒尺寸.

1.2 晶体塑性模型(CP)

晶体塑性模型描述了晶体在弹塑性变形过程中应力应变的关系.晶体塑性的机理与塑性变形后发生的不可逆的硬化密切相关.基于Schmid 定律，Peirce 等人[10]提出了粘塑性率相关模型来描述金属硬化过程，即

为描述滑移系开动对自身和滑移系间相互作用的影响，分别引入了自硬化、潜硬化模量，即

式中：h0是 初始硬化模量，τ0是屈服应力；τs是硬化过程的阶段I应力；γ是所有滑移系的累积剪切应变；q是硬化常量.

2 宏观-微观跨尺度短裂纹演化仿真

2.1 有限元建模

为应用上述基于FIP的短裂纹扩展模型和晶体塑性本构，并验证其有效性和合理性，针对文献[11]中的十字形焊接接头试件开展焊趾疲劳短裂纹演化的跨尺度仿真.该试件的母材采用热轧低合金钢Q345B，其屈服强度和抗拉强度分别为345 MPa 和416 MPa.金相检测表明焊趾区域组织主要由BCC 结构的铁素体组成，其晶粒为不规则的多边形，晶粒平均尺寸为21.1 μm.文献中，该试件薄板施加了2 级载荷谱块的循环拉伸载荷.其中首个基线载荷谱块经历的循环次数为疲劳短裂纹阶段，对应的应力变程为200 MPa，应力比为0.

为了精确模拟焊趾局部微观晶粒层面的裂纹成核和裂纹扩展过程，采用宏观模型和微观RVE 子模型相结合的建模技术，如图1 所示.具体说，首先建立十字形焊接接头宏观模型.其中，十字形焊接接头总长为180 mm，总宽为80 mm.通过整理文献[11]疲劳试验中十字形焊接接头焊趾半径的测量的数据，焊趾半径均值为0.61 mm.因此仿真验证中焊趾半径取0.6 mm，作为与试验对应.另外，宏观模型施加与试验相同的循环载荷.考虑到宏观模型的结构特点和载荷边界，全局网格采用平面应变单元，全局单元尺寸为0.2 mm(即200 μm).为了确保焊趾RVE 子模型的位移边界条件的准确性，在需建立RVE 子模型的焊趾局部，进行切分处理并采用二次完全积分的四边形单元来局部细分，局部单元尺寸为0.004 mm(即4 μm).

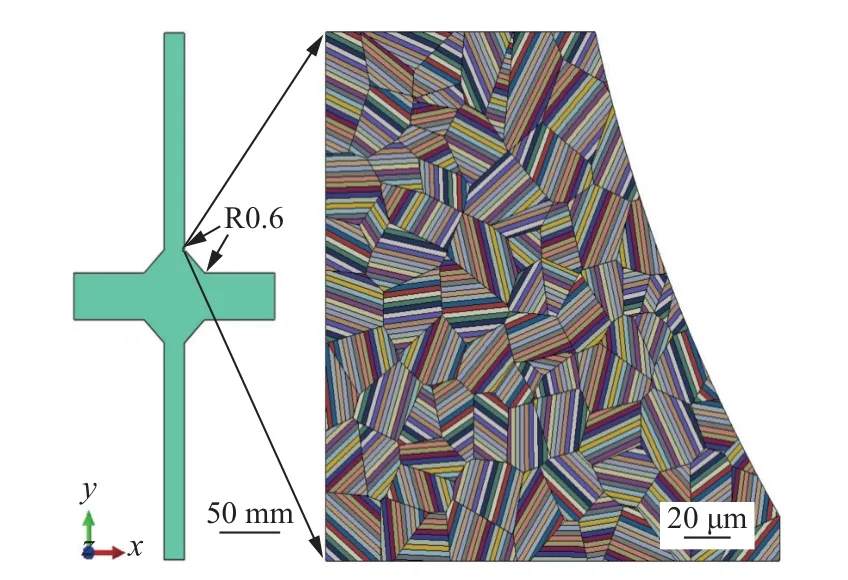
图1 有限元跨尺度建模Fig.1 Cross-scale finite element modeling

然后，建立焊趾局部的微观RVE 子模型，取自对应焊趾半径的宏观模型中疲劳短裂纹易萌生的焊趾区域，其中左边长和下边长为0.2 mm(即200 μm).RVE 子模型除了焊趾圆弧边界的自由表面不受力，其余各边界的位移边界条件来自于宏观模型焊趾局部相应坐标的位移结果.基于泰森多边形法，在焊趾RVE 子模型中随机布置晶粒种子并划分晶粒.晶粒平均尺寸为0.021 mm(即21 μm).并且，每个晶粒内部均分别根据其晶粒取向预定义了相互平行的驻留滑移带(PSBs)，宽度均为0.002 mm(即2 μm).为保证计算的准确性和收敛性，网格采用二次完全积分的平面应变单元，晶粒内部以四边形单元划分，晶界处采用三角形单元过渡，单元尺寸均为0.001 mm(即1 μm).

2.2 用户自定义材料参数

一般地，在循环载荷下十字形焊接接头宏观模型大部分区域处于弹性变形阶段.因此，宏观模型赋予Q345B 材料参数为弹性模量205 GPa，泊松比0.28.

然而，在焊趾局部已进入塑性变形阶段，同时考虑焊趾局部微观结构影响，焊趾RVE 子模型采用Huang[12]的晶体塑性模型.具体说，对于每个晶粒中每条滑移带都需要赋予独立的用户自定义材料参数，包括：弹性矩阵参数、滑移系向量参数、初始晶粒取向、硬化模型参数、数值求解参数、FIP及寿命计算的参数.考虑BCC 晶体的对称性，对RVE 子模型中的晶粒赋予随机取向.另外，BCC 晶体最多有48 个滑移系，但是对于铁素体晶体只有{110}[111] 12 组滑移系能够在室温下稳定启动，所以文中只考虑{110}[111] 12 组滑移系，其特性参数[13]如表1 所示.

表1 铁素体{110}[111]滑移系特性参数Table 1 Characteristic parameters of ferrite {110}[111] slip system

2.3 短裂纹演化仿真流程

采用基于FIP的短裂纹扩展模型，疲劳短裂纹演化仿真流程是首先利用子模型技术，在焊趾RVE 子模型边界施加来自宏观模型焊趾区域的位移结果.然后，通过公式(3)计算每一个晶粒中所有PSBs 的成核寿命，或通过公式(5)计算扩展寿命，其中的最小寿命定义为裂纹成核寿命或裂纹扩展寿命.将具有最小寿命的PSB 确认形成裂纹，并通过降低其弹性模量来模拟裂纹形成(弹性模量采用各向同时折减99.99%).继续施加循环载荷，使得应力重分布.循环上述步骤，当裂纹到达RVE 边界时仿真结束.相连的多条PSBs 可作为焊趾RVE 的疲劳短裂纹，其不可逆损伤累积量即RVE 疲劳寿命.

2.4 仿真结果

图2a 显示了焊趾半径为0.6 mm 的焊趾RVE子模型在裂纹成核阶段基于滑移带平均的Von Mises 应力分布.从整体分析，RVE 内部Von Mises应力分布呈现不均匀性.这种不均匀性在晶粒间与晶粒内均有体现.具体来说，晶粒间的不均匀性反映了相邻晶粒间的取向差.晶间取向差越大，微观Von Mises 应力分布不均匀性越明显.晶粒内的不均匀性是由于晶粒内部各滑移带滑移受到周围晶界的阻碍影响.Von Mises 应力数值水平较高的晶粒多集中在RVE 内部.然而在容易发生裂纹成核的焊趾圆弧边界，晶粒的Von Mises 应力相比RVE 内部普遍较低.Von Mises 应力无法很好表征疲劳微观短裂纹的演化行为.图2b 显示了焊趾半径分别为0.6 mm 的焊趾RVE 子模型在裂纹成核阶段的基于滑移带平均的FIP分布.整体分析，在焊趾圆弧边界附近，平均FIP数值较高(灰色与红色)；远离焊趾圆弧边界，平均FIP数值较低(蓝色).因此，基于滑移带平均的FIP参量相比于Von Mises 应力能够更好地描述疲劳短裂纹大多成核于材料表面这一试验现象.

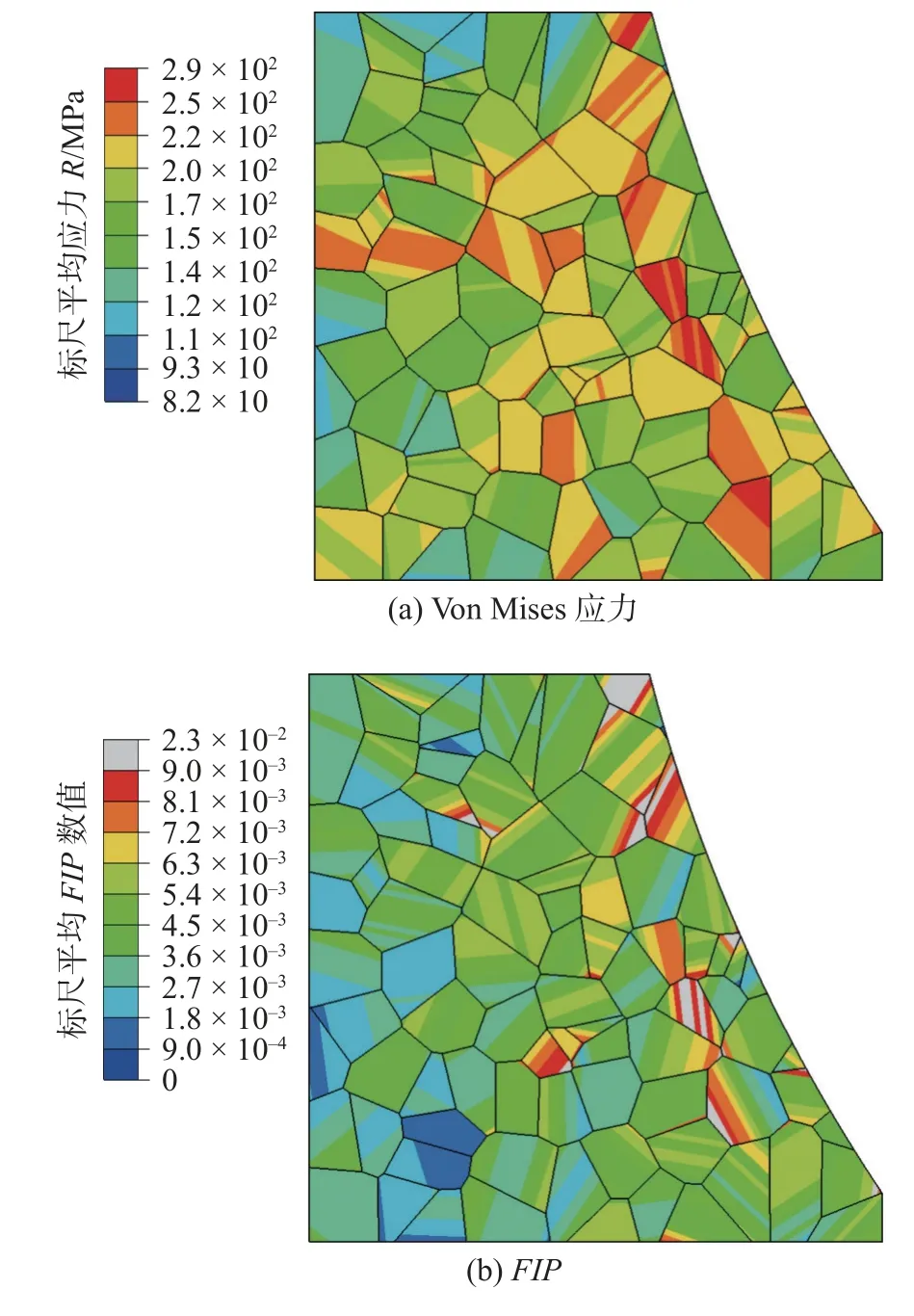
图2 基于滑移带平均的结果参量Fig.2 Result parameter of PSB-based average.(a) Von Mises;(b) FIP

对焊趾RVE 子模型进行逐晶粒地裂纹演化仿真，结果如表2 所示.经过41.27 万次循环后裂纹投影长度达到105.93 μm，文献[11]中当循环次数32.50 万次时裂纹扩展深度为110 μm 左右，二者结果相近.可以得出，综合Huang 的晶体塑性模型和基于FIP的短裂纹扩展模型的宏观-微观跨尺度的疲劳短裂纹演化仿真具有合理性和有效性.另外，首个驻留滑移带的循环次数(14.74 万次)在裂纹总循环次数(43.31 万次)中占比最大，即裂纹成核寿命消耗了RVE 疲劳寿命的大部分(34.03%).

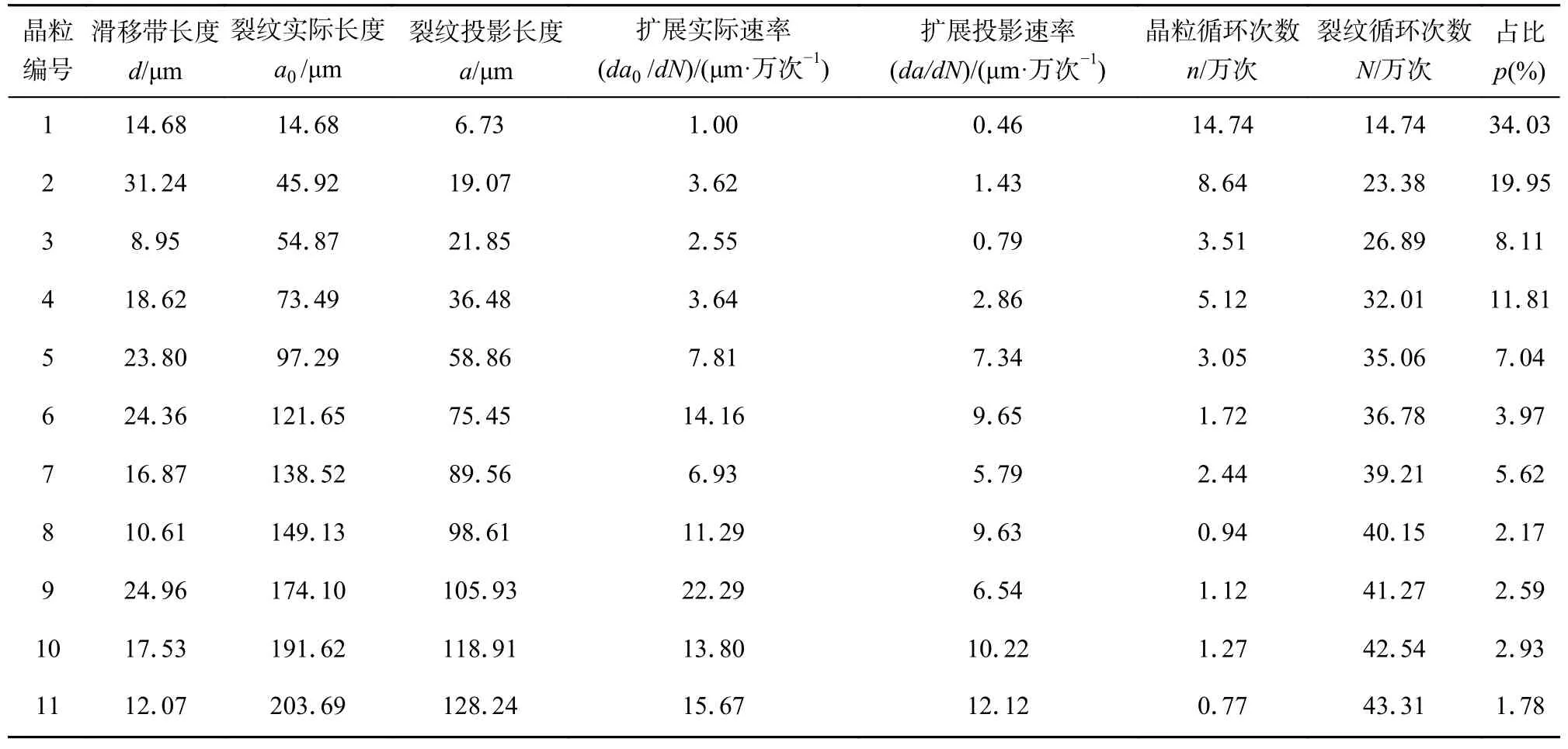
表2 裂纹演化仿真结果(R=0.6mm)Table 2 Simulation results of crack evolution (R=0.6mm)

分析裂纹投影长度、扩展投影速率随裂纹循环次数的变化，如图3 所示.在裂纹扩展前期，裂纹投影长度和扩展投影速率均处于较低的数值水平，同时裂纹投影扩展速率变化平缓；随着裂纹扩展，即逐渐远离焊趾圆弧边界，扩展投影速率呈现较大波动性，但总体呈现上升趋势，反映了此阶段裂纹扩展受到了晶粒取向和晶粒形态的较大影响.

图3 微观短裂纹投影长度与扩展投影速率Fig.3 Crack length and propagation rate in projection direction in MSC

3 焊趾半径的影响

通常，焊趾半径直接影响焊趾局部的应力集中程度，进而影响裂纹的演化行为.为了研究其影响，以0.1 mm 为步长，模拟了焊趾半径为0.1～ 1.0 mm的10 个十字形焊接接头试件的宏观-微观跨尺度疲劳过程.由于焊趾半径与RVE 几何形状密切相关，导致RVE 圆弧边界的晶粒形态不可避免地发生变化.因此，为了减少晶粒形态和取向等因素对焊趾区域裂纹成核和扩展的影响，在焊趾RVE 的建模过程中，首先确保模型在RVE 内部保持晶粒形态与取向不变，同时尽可能使圆弧边界上同一位置的晶粒具有类似的几何形状和一致的晶粒取向.仿真结束后，从裂纹成核阶段、裂纹扩展路径、裂纹扩展速率与疲劳寿命4 个方面展开分析.

3.1 裂纹成核阶段

图4 显示了焊趾半径分别为0.2、0.4、0.6 和0.8 mm 的焊趾RVE 子模型在裂纹成核阶段的疲劳寿命云图，其中，成核阶段定义为首个晶粒开裂的过程，且采用的控制参量为基于滑移带平均的FIP指标.研究[14-15]认为，在焊缝区，裂纹深度达到0.1mm 的范围定义为微观短裂纹阶段.另外，根据文献[11]试验结果，当十字形焊接接头的裂纹深度达到0.1 mm 时，裂纹循环次数在30 万次左右.由此，可将焊趾RVE 子模型划分为焊趾圆弧影响区和非影响区.可以发现，不同焊趾半径RVE 子模型的影响区宽度变化不大.

图4 不同焊趾半径的疲劳寿命分布云图Fig.4 Fatigue life distribution diagram of different weld toe radius.(a) R=0.2mm;(b) R=0.4 mm;(c) R=0.6 mm;(d) R=0.8 mm

在影响区内，随着焊趾半径的增大，焊趾半径对疲劳寿命的影响力逐渐减小.而且，在影响区内随着与焊趾圆弧边界距离的增加，各个RVE 子模型中对应晶粒的寿命逐渐趋同，表明成核阶段焊趾半径对疲劳寿命的影响主要局限在焊趾表面附近.由于焊趾局部的应力集中，首先裂纹成核(即具有最小寿命值的滑移带)的晶粒均位于焊趾圆弧边界，但对应晶粒的所在部位有所不同.成核寿命呈现随焊趾半径的减小而不断减小的趋势，以0.8 mm RVE 的成核寿命为基准，0.6 mm、0.4 mm、0.2 mm RVE 的寿命下降比值分别为19.37%、17.18%、81.95%.

针对焊趾半径对焊趾圆弧边界寿命的影响进一步分析，包括了焊趾半径为0.1～ 1.0 mm 十个焊趾RVE 子模型，统计裂纹成核阶段焊趾圆弧边界上前30 个寿命最小的滑移带，如图5 所示.整体来看，随着焊趾半径增大，箱形图中寿命数据范围、四分位距和须线呈现不断增大的趋势，即寿命分散性呈逐渐扩大趋势，表明晶粒形态与取向随着焊趾半径增大而逐渐成为影响疲劳寿命的主导因素.箱形图数据范围的下限值代表了焊趾RVE 的成核寿命.当焊趾半径小于0.5 mm 时，成核寿命和均值寿命随着焊趾半径增大而增大，反映该范围主要受到焊趾半径影响；当焊趾半径大于0.5 mm 时，成核寿命和均值寿命随焊趾半径变化出现波动性变化，反映出此时焊趾圆弧边界上晶粒形态与取向的影响相比焊趾半径的影响更大.

3.2 裂纹扩展路径

从上述分析可知，焊趾半径小于0.5 mm 时，疲劳短裂纹演化行为受到焊趾半径的影响较大.因此，取焊趾半径0.1、0.2、0.3 和0.4 mm 4 组RVE 子模型研究焊趾半径对裂纹扩展阶段的影响.

如图6 显示了焊趾半径分别为0.1、0.2、0.3和0.4 mm 焊趾RVE 子模型的裂纹扩展路径.整体分析，不同焊趾半径的RVE 短裂纹扩展趋势一致，即疲劳短裂纹总体上从焊趾半径影响区成核，并呈一定角度朝斜下方曲折扩展到非影响区.具体来说，裂纹扩展前期在影响区内受到焊趾圆弧边界的影响，不同焊趾RVE 裂纹成核位置有所不同，但是均在焊趾圆弧边界上.随着裂纹扩展，由于晶间取向差异产生路径偏折，不同焊趾半径RVE 裂纹路径穿过晶粒的编号和数量有所差异.裂纹达到焊趾圆弧非影响区后，焊趾半径的影响较弱，且晶粒形态和取向完全一致，裂纹扩展路径后期趋于一致.

图6 焊趾半径对裂纹扩展路径影响Fig.6 Crack propagation path of different welding toe radius.(a) R=0.1mm;(b) R=0.2 mm;(c) R=0.3 mm;(d) R=0.4 mm

3.3 裂纹疲劳寿命与扩展速率

分析焊趾半径对疲劳短裂纹扩展速率与疲劳寿命影响，分别绘制0.1、0.2、0.3 和0.4mm 焊趾RVE 子模型裂纹投影长度与裂纹循环次数、扩展投影速率与裂纹投影长度的关系曲线，如图7 所示.整体来看，以裂纹投影长度达到100 μm 为基准，随着焊趾半径的增大，疲劳短裂纹寿命呈现逐渐增大的趋势，裂纹扩展速率呈现逐渐减小.具体来说，在影响区内，裂纹扩展前期主要受到焊趾圆弧边界的影响，扩展速率呈现线性增长.随着裂纹扩展，裂纹尖端逐渐远离焊趾圆弧边界，晶粒形态与取向的影响逐渐增大，裂纹扩展速率呈现上升趋势，其波动性随焊趾半径增大逐渐增大.

图7 焊趾半径对裂纹扩展阶段行为的影响Fig.7 Effect of welding toe radius on crack propagation behavior.(a) crack length in projection direction;(b) propagation rate in projection direction

4 结论

(1) 综合了子模型技术和晶体塑性模型，计算了基于滑移带平均的FIP参量，以最小驻留滑移带寿命为驱动，实现了宏观-微观跨尺度的疲劳短裂纹演化行为仿真，获得了与疲劳试验接近的裂纹长度与循环次数，验证了该方法的可行性和有效性.

(2) 研究了焊趾半径对疲劳短裂纹成核阶段的影响.结果表明：不同焊趾半径的RVE 子模型的裂纹成核位置有所差异，但均在焊趾圆弧边界.当焊趾半径小于0.5 mm 时，成核寿命随着焊趾半径增大而增大；当焊趾半径大于0.5 mm 时，晶粒形态与取向的影响大于焊趾半径的影响，成核寿命呈现波动性变化.

(3) 研究了焊趾半径对疲劳短裂纹扩展阶段的影响.结果表明：焊趾RVE 子模型可划分为焊趾圆弧影响区和非影响区.在影响区，焊趾半径影响较大，裂纹扩展行为主要受到焊趾圆弧边界影响，而受到晶粒形态与取向的影响较小，导致此区域的裂纹扩展路径有所差异，同时扩展速率随裂纹循环次数呈线性上升.随着裂纹扩展，裂纹尖端逐渐远离焊趾圆弧边界，焊趾半径影响逐渐减小，晶粒形态与取向影响逐渐增大.当裂纹扩展到非影响区，扩展路径趋于一致，同时扩展速率呈现波动性上升趋势，反映了在该区域裂纹扩展行为主要受到晶粒形态与取向影响.