基于主S-N曲线的带止裂槽焊接接头疲劳寿命预测及改进

任浩 卢序鑫 聂春戈 刘燕

摘要：以带止裂槽焊接接头为研究对象，提取可能发生疲劳失效的焊趾截面、焊喉截面和止裂槽截面的节点力，基于主S-N曲线法求解截面的等效结构应力，评估焊缝的疲劳寿命，并提出改进接头的建议。分析发现：止裂槽的存在会显著增加局部位置的应力，导致疲劳寿命明显降低。填充止裂槽并适当增大水平方向焊脚尺寸，可以提高该位置疲劳寿命10倍左右。

关键词：主S-N曲线; 焊趾; 焊喉; 止裂槽; 疲劳

中图分类号：TG407;TB115.1

文献标志码：B

Fatigue life prediction and improvement of welded joint with anti-crack groove based on master S-N curve

REN Hao， LU Xuxin， NIE Chunge， LIU Yan

（College of Locomotive and Vehicle Engineering， Dalian Jiaotong University， Dalian 116028， Liaoning， China）

Abstract：

Taking the welded joint with anti-crack groove as the research object， the joint forces of welding toe section， welding throat section and anti-crack groove section which may be fatigue failure are extracted. Based on the master S-N curve method， the equivalent structural stresses of the cross sections are calculated， and the fatigue life of the welded joint is evaluated. The suggestions for improving the welded joint are put forward. It is found that the anti-crack groove can significantly increase the stress in the local position， which can obviously reduce the fatigue life. By filling the anti-crack groove and properly increasing the size of the horizontal weld foot， the fatigue life of this position can be increased by about 10 times.

Key words：

master S-N curve; welding toe; welding throat; anti-crack groove; fatigue

收稿日期：2019-05-20

修回日期：2019-07-11

基金項目： 国家自然科学基金（51405057）;国家重点研发计划（2017YFB1201303）;辽宁省自然科学基金（20170540121，20170540137）

作者简介：

任浩（1994—），男，山西大同人，硕士研究生，研究方向为车辆关键技术及其CAE，（E-mail）357133286@qq.com

0 引 言

基于有限元法对焊接结构进行疲劳评估需要解决2个问题：（1）使用哪一条S-N曲线;（2）应力如何计算。[1]对于名义应力法和热点应力法，基于分类方法选择S-N曲线在分析复杂结构时存在较大的随意性，这是因为实际的焊接接头与标准中有限数量的简单接头存在较大差别，难以确定合适的S-N曲线。从应力计算的角度看，接头的名义应力在复杂结构的焊接接头中难以定义或不存在;而热点应力的计算存在较强的网格敏感性，即网格的尺寸和形状与单元类型对计算结果影响很大，导致最终计算结果的可靠性不高。因此，这2种方法在实际应用中均存在较大的局限性。

主S-N曲线法可很好地解决上述问题，获得可靠性更高的计算结果。

1 主S-N曲线法

1.1 网格不敏感结构应力的定义

角焊缝附近往往是结构刚度发生变化的位置，应力状态复杂，应力集中现象非常普遍，也是常规有限元法容易应力奇异的位置。[2]以焊趾截面法向应力为例，有限元的应力计算结果可以分解为线性应力和高阶自平衡应力2部分，其中线性应力又可以分解为膜应力σm和弯曲应力σb这2部分。线性应力可利用有限元法的单元节点力计算，称为结构应力。[3]焊趾截面的典型应力定义见图1，其中τ（y） 和σx（y）分别为沿厚度方向的剪切力和应力。

由于计算时利用单元节点力，保证应力计算结果满足平衡条件，因此结构应力的计算结果应表现出良好的网格不敏感性，即网格尺寸和单元类型对结果的影响较小。某承载角焊缝十字接头[4-5]见图2。使用不同的网格尺寸，分别计算焊趾位置的法向结构应力和45°焊喉截面的剪切膜应力。计算采用3种网格尺寸，分别在截面厚度方向生成1、2和4个网格，并与常规有限元应力计算结果进行对比，验证结构应力的网格不敏感性，结果见图3。

由图3可知：使用不同网格尺寸的有限元模型，焊趾位置法向结构应力的有限元计算结果差异很大，而基于单元节点力的计算却非常一致;同样，对于45°焊喉截面，剪切膜应力计算结果也非常一致，证明结构应力对网格尺寸不敏感。[3]

1.2 等效结构应力与主S-N曲线

基于断裂力学原理，可推导出等效结构应力与疲劳寿命之间的理论关系，即主S-N曲线方程为

N=（Cd/ΔSs）1/h

（1）

式中：N为疲劳寿命值;Cd和h为试验常数;ΔSs为等效结构应力变化范围。

ΔSs=Δσst（2-m）/2m ·I（r）1/m

（2）

r=ΔσbΔσs=ΔσbΔσm+Δσb

（3）

式中：Δσm和Δσb分别为膜应力范围和弯曲应力范围;m为试验常数，m=3.6。

由式（2）可以看出，等效结构应力变化范围ΔSs受结构应力变化范围Δσs、板厚t和应力状态I（r）等3个参数的综合影响。

主S-N曲线方程与名义应力法S-N曲线方程形式相同[6]，但主S-N曲线方程以等效结构应力变化范围ΔSs为参数，包含结构应力变化范围、板厚和应力状态的综合影响。当取h=0.319 50时，钢材焊接接头的主S-N曲线参数见表1。

1.3 应力集中因数

等效结构应力变化范围也可以写为

ΔSs=Δσst（2-m）/2m ·I（r）1/m =FsΔσnt（2-m）/2m ·I（r）1/m

（4）

式中：Δσn为传统名义应力，如F/A;Fs为基于结构应力的应力集中因數或单位载荷（如F/A=1）作用下计算的结构应力，即

Fs=ΔσsΔσn

（5）

为方便将应力集中因数与接头疲劳寿命相关联，提出基于等效结构应力的应力集中因数，其定义为

Fes =Fst（2-m）/2m ·I（r）1/m

（6）

2 止裂槽对焊缝疲劳寿命的影响

2.1 止裂槽几何模型

止裂槽有助于控制钣金件材料的变形行为，并防止材料发生意外变形，因此在实际设计中不可避免。对止裂槽进行焊接时，止裂槽的存在会影响焊缝的疲劳寿命。止裂槽附近实际几何形状复杂（见图4），若直接取局部结构进行分析，则无法计算所关心位置的结构应力，意味着无法量化分析接头的疲劳寿命。因此，在分析过程中应先用平面模型找出疲劳失效截面的位置，再用三维简化模型评估止裂槽对疲劳寿命的影响。[7]

2.2 平面模型

根据对称性，分别建立含间隙（模拟止裂槽）和无间隙（完全填充）的十字接头的1/4有限元模型，见图5。模型中水平板与竖直板之间只通过焊缝连接，2个板之间的节点没有连接，不直接传递载荷。图5还给出预期疲劳失效截面的位置。

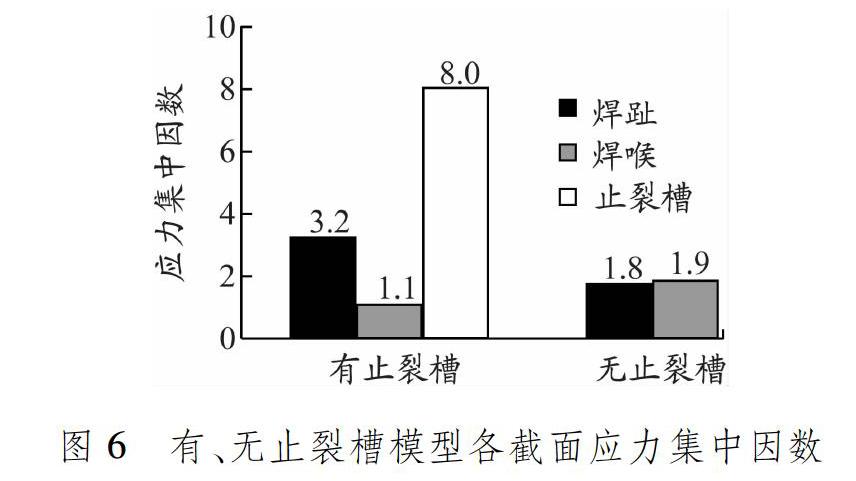
计算2个接头在水平拉伸载荷作用下各截面的应力集中因数，以此判断接头中的薄弱截面，并初步对比2种接头的疲劳寿命。这里只简单判断和估算，因此使用基于结构应力的应力集中因数Fs，其定义为截面结构应力σs除以水平板的名义应力（即平均应力）σn。2个模型各截面应力集中因数计算结果见图6。

对于有止裂槽模型，可能的失效位置为焊趾截面A1、焊喉截面A2和止裂槽位置的截面A3。3个截面的应力集中因数分别为3.3、1.1和8.0，表明止裂槽位置截面A3的疲劳可靠性明显偏低，是接头中的疲劳薄弱位置。

对于无止裂槽模型，可能的失效位置为焊趾截面B1和焊喉截面B2，2个位置的应力集中因数分别为1.8和1.9，表明2个截面的疲劳可靠性相当，焊喉截面B2疲劳寿命稍低。

与无止裂槽的理想模型相比，有止裂槽模型的最大应力集中因数是理想模型的4.2倍。根据结构应力与疲劳寿命之间3次方的关系，由于止裂槽的存在，接头的疲劳寿命约降低几十分之一。

2.3 三维止裂槽接头模型

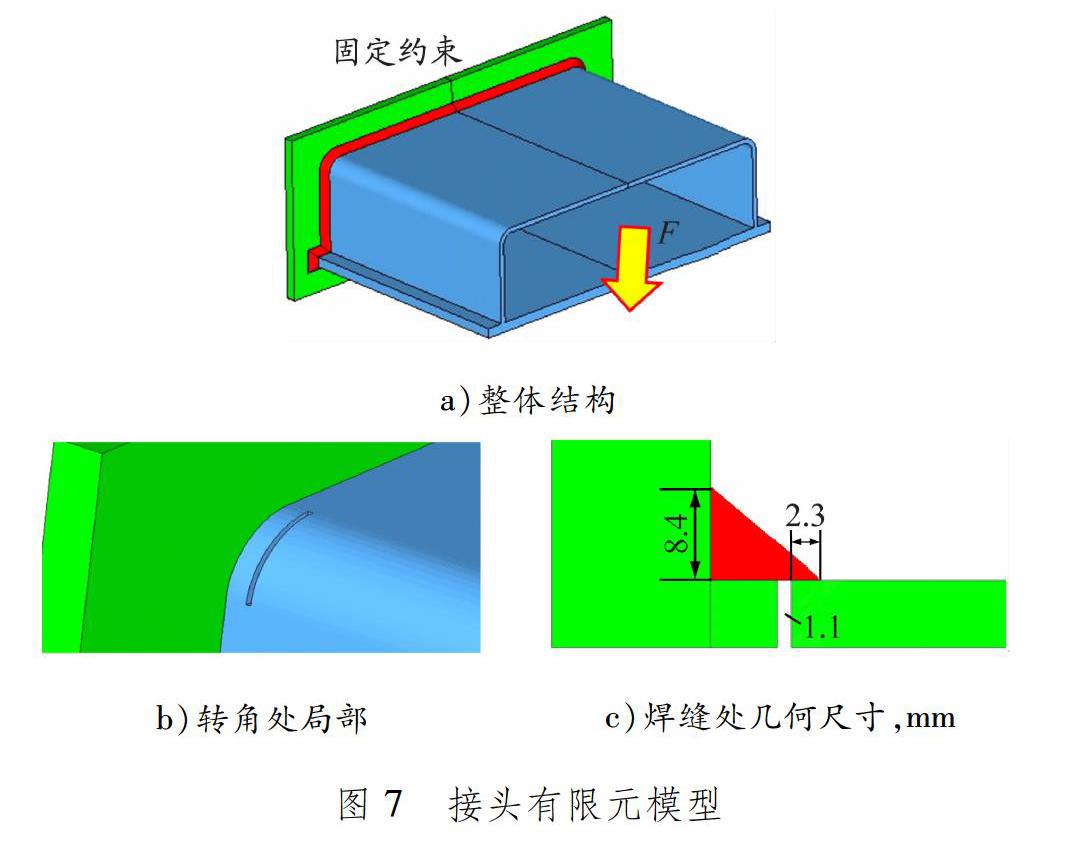
对模型进行适当简化，尽量反映实际结构中止裂槽的受力特征，得到的接头有限元模型见图7。

模型本质上是一个梁截面（计算时取1/2），截面端部与竖直板通过焊缝连接，间隙（止裂槽）位于转角位置。截取整条焊缝中受止裂槽影响的一段（160～240 mm），各个截面位置的结构应力计算结果见图8。

由此可知：当结构中有止裂槽时，止裂槽截面的结构应力最大，是疲劳薄弱位置;止裂槽截面的最大结构应力是无止裂槽模型最大结构应力的2.5倍，意味着由于止裂槽的出现，接头的疲劳寿命仅为理想接头疲劳寿命的1/10。

3 结构改进方案的疲劳寿命估算

3.1 平面模型

前文的分析说明，平面模型的计算结果过于保守，但是由于平面模型比较简单、容易理解，所以可以先以平面模型初步预测改进方案，再利用三维止裂槽接头模型进行详细分析。

根据前文的分析，焊接接头的疲劳寿命之所以很低，在于止裂槽截面承载面积过低，因此可以将止裂槽进行打磨后填充[8-10]，以提高接头寿命。填充止裂槽示意见图9。

为此，建立4个不同的有限元模型（见图10），其中：模型1为含初始间隙模型;模型2为填充间隙2.3 mm的模型;模型3为填充间隙4.0 mm的模型;模型4为填充间隙4.0 mm，同时增加水平方向焊脚尺寸的模型。各个模型均已标注计算结构应力的截面位置。

为与接头疲劳寿命关联，给出基于等效结构应力的应力集中因数，见图11。

由图11a）可知，各模型最大应力位置不同，模型1的最大应力位置在止裂槽处，模型2的最大应力位置在焊趾处。各接头的疲劳寿命取决于最大等效结构应力。由图11b）可知，模型1～4的最大等效结构应力逐渐降低，意味着疲劳寿命逐渐提高，其中模型4的疲劳寿命最高。

因此，可利用模型4的优化方案评估优化后的接头疲劳寿命。

3.2 三维止裂槽接头模型

根据第3.1节的分析，建立改进后的三维止裂槽接头模型，见图12。

在改进后的接头模型中，止裂槽的填充深度为4.0 mm，水平方向焊脚尺寸增加4.0 mm。为方便对比，同时计算初始无填充时的模型等效结构应力，结果见图13。

由2种接头计算结果对比可知：改进后的接头通过填充止裂槽并增大水平方向焊脚尺寸，最大等效结构应力出现在焊趾处，为8.9 MPa;初始接头的最大等效结构应力出现在止裂槽处，为21.4 MPa，是改进接头的2.4倍。根据式（1）等效结构应力和疲劳寿命的关系，2种接头的疲劳寿命之比为16.5，即改进后接头的疲劳寿命可以提高到原寿命的16.5 倍。即使考虑安全系数为1.5，改进后接头的疲劳寿命也可以提高10倍以上，因此认为改进方案可行。

4 结 论

（1）止裂槽的存在会显著增加局部位置的应力，导致疲劳寿命明显降低，其本质是止裂槽位置焊缝承载面积显著减小。

（2）填充止裂槽并保证有效填充深度（4 mm左右），适当增大水平方向焊脚尺寸（3～4 mm），可以提高该位置疲劳寿命10倍左右。

参考文献：

[1]魏德永， 张志远， 聂春戈， 等. 基于主S-N曲线法的驱动桥焊接结构疲劳耐久性分析评价方法应用研究[C]// 2018中国汽车工程学会年会论文集. 上海： 中国汽车工程学会， 2018： 1967-1974.

[2]聂春戈， 马思群， 孙彦彬， 等. 正面角焊缝接头的静力强度與尺寸设计研究[J]. 河北科技大学学报， 2015， 36（5）： 474- 479. DOI： 10.7535/hbkd.2015yx05005.

[3]兆文忠， 李向伟， 董平沙. 焊接结构抗疲劳设计理论与方法[M]. 北京： 机械工业出版社， 2017： 23-25.

[4]聂春戈， 孙振轩， 孙彦彬， 等. 考虑疲劳性能的十字接头角焊缝尺寸设计[J]. 焊接学报， 2017， 38（11）： 16-20. DOI： 10.12073/j.hjxb.20170227003.

[5]聂春戈， 魏鸿亮， 董平沙， 等. 基于结构应力方法的正面角焊缝抗剪强度分析[J]. 焊接学报， 2015， 36（1）： 70-74.

[6]孙权， 陈秉智. 基于主S-N曲线法的地铁制动箱焊接疲劳分析[J]. 计算机辅助工程， 2016， 25（3）： 47-51. DOI： 10.13340/j.cae.2016.03.009.

[7]RAMUM， PRABHU R V， THYLA P R， et al. Studies on effect of weld defect on fatigue behavior of welded structures[J]. China Welding， 2018， 27（1）： 53-59. DOI： 10.12073/j.cw.20170614001.

[8]聂春戈， 陈秉智， 兆文忠. 机车焊接构架变形矫正的弹塑性有限元分析[J]. 大连交通大学学报， 2008， 29（5）： 55-58.

[9]聂春戈， 李晓峰， 兆文忠. 高速转向架轴箱转臂结构拓扑优化设计[J]. 机械设计， 2007， 24（6）： 58-60.

[10]WANGJ， ZHAO W Z. Master S-N curve method based optimization design of weld structure[C]// Proceedings of 2011 4th International Joint Conference on Computational Science and Optimization. Kunming： IEEE， 2011： 12122552. DOI： 10.1109/CSO.2011.164.