基于电荷泵的压电致动器迟滞非线性改善研究

张连生, 张鹏程, 郝 爽, 黄强先, 程荣俊, 李红莉

(1.合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009；2.合肥工业大学 测试理论与精密仪器安徽省重点实验室，安徽 合肥 230009)

1 引 言

压电致动器因其尺寸小、精确度高、输出力大、频率响应快等优点[1],而被广泛应用于精密定位、微纳米测量等领域[2, 3]。随着精密工程和微纳米技术的不断发展,压电致动器已经成为很多前沿科技的核心驱动单元,大大推动了高科技产业的不断发展[4, 5],因此研究压电致动器的驱动方法显得尤为重要。

在电压驱动下,压电致动器自身具有的迟滞特性严重影响了定位精度,为了解决压电致动器输出位移与输入电压之间的迟滞非线性问题[6],国内外学者进行了大量的实验和研究,目前针对压电陶瓷的控制方法主要有基于电压控制的开环前馈控制方法[7]和反馈控制方法[8],以及电荷控制法[9]。采用开环前馈控制方法需要建立精确的非线性模型[10],反馈控制方法虽然可以实现较高精度的控制[11],但是需要高精度位移传感器,系统的成本较高[12];电荷控制法利用压电陶瓷的位移与其两端的电荷量成近似线性的特点,可以减小压电陶瓷的迟滞非线性[13],不过该方法由于缺少直流通路容易产生输出饱和。

哈尔滨工业大学杨琛等提出了一种非线性电荷控制方法[14],通过对传统电荷驱动方法输入电压的调节使压电致动器两端的电荷量呈现一定的非线性,进而改善传统电荷驱动的迟滞非线性,该方法存在的问题是电路较为复杂,同时需要添加反馈控制,成本较高。中国科学技术大学黄亮等提出了一种电荷泵驱动电路[15,16],通过该电路控制压电陶瓷两端电荷量的增减相较于传统电荷控制迟滞得到了进一步的改善,但该方法控制压电陶瓷输出位移仍然存在一定的迟滞非线性,并且在电压工作范围较大时迟滞非线性呈现增大的趋势。

本文从电荷泵的工作原理出发,研究了经典电荷泵驱动下残余迟滞的大小和规律,提出了一种改进的电荷泵补偿方法,介绍了改进的电荷泵补偿方法的基本原理,阐述了校正参数的推导方法并设计了校正补偿实验。实验结果表明该方法可以有效改善经典电荷泵驱动下压电致动器的迟滞非线性特性,具有较好的应用价值。

2 经典电荷泵的残余迟滞

经典电荷泵驱动利用压电致动器两端电荷量与输出位移之间近似线性的特性,通过控制压电致动器两端电荷量的线性增减实现输出位移的控制。电荷泵电路基本原理图如图1所示,通过模拟开关S1控制压电致动器两端电荷量的增减,再通过模拟开关S2控制压电致动器两端电荷量的增减速率。

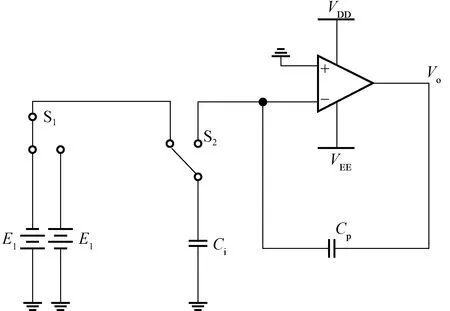
图1 电荷泵电路基本原理Fig.1 Basic principle of charge pump circuit

采用电压范围为0～100 V的电荷泵驱动信号驱动压电致动器。当给定驱动信号频率为1 Hz时,迟滞实验结果如图2所示,其中横坐标表示压电致动器的驱动时间,纵坐标表示其输出位移。从经典电荷泵的输出位移曲线可以看出,经典电荷泵驱动仍然存在一个较大的残余迟滞,同时具有明显的非线性。其余频率的实验结果详见表1。

表1 不同频率时经典电荷泵的迟滞大小Tab.1 Hysteresis of different frequency under classical charge pump driving method

图2 经典电荷泵驱动的迟滞曲线Fig.2 Hysteresis curve driven by classical charge pump

给定频率为1 Hz的经典电荷泵驱动信号,实验发现随着驱动电压范围的增大,压电致动器输出位移曲线的迟滞呈现增大的趋势,如表2所示。这是因为随着驱动电压范围的增大,压电致动器两端的电场强度不断增大,由压电致动器的铁电效应可知,随着电场强度的增大造成压电致动器迟滞非线性呈现增大的趋势[17]。

表2 不同电压范围时经典电荷泵的迟滞大小Tab.2 Hysteresis of different voltage ranges under classical charge pump driving method

3 改进的电荷泵驱动方案设计

如图1所示,电荷泵电路开关S2每切换一次充入压电致动器两端的电荷量为:

Q=E·Ci

(1)

式中:E为基准电压源大小;Ci为开关电容模块的充放电电容大小。

压电致动器两端输入电荷量速率为:

K=E·Ci·f2

(2)

式中:f2为开关S2的切换频率。

控制开关S2的切换频率即可控制压电致动器两端电荷量的变化速率,从而达到控制输出位移曲线斜率的目的。在驱动过程中,通过调整输出位移斜率,即为开关S2的切换频率f2,即可改善经典电荷泵电路的迟滞非线性。

南京工程学院的王建红[17]及长春建筑学院的王丽娜[18]等通过实验验证二阶多项式拟合的方法可以较高精度地拟合压电致动器的迟滞特性曲线,本文采用二阶多项式拟合得到如图2所示的输出位移曲线:

x(t)=at2+bt+c

(3)

其中:x(t)为压电致动器的输出位移;t为驱动时间;a、b、c为拟合系数。

输出位移的斜率为:

(4)

改进电荷泵的系统框图如图3所示,主要包括基准电压模块、开关电容模块、高压运放模块、逻辑比较模块、迟滞校正模块和压频转换模块。

图3 改进的电荷泵系统框图Fig.3 Improved charge pump system block diagram

基准电压模块主要由正负基准电压和模拟开关S1组成,通过控制模拟开关S1实现正负基准电压的切换。开关电容模块主要由充放电电容Ci和模拟开关S2组成,通过控制模拟开关S2的切换实现电荷泵电路充放电速率的调节。

高压运放模块主要由高压运算放大器组成,其作用是中和掉充放电电容上的电荷,并在压电致动器两端感应出等量的电荷。逻辑比较模块检测电荷泵电路的正反行程位移,产生区分正反行程的方波信号并作为开关S1的控制信号控制基准电压模块的正负基准电压的切换。迟滞校正模块接收逻辑比较模块的方波信号并确定迟滞修正系数,产生随时间线性变化的电压信号,并将该信号传递给压频转换模块。压频转换模块将迟滞校正模块产生的线性变化的电压信号转化为变化的频率信号,用该信号控制模拟开关S2即可实现电荷泵电路充放电速率的调节。实验中采用LTC6990作为压频转换芯片,该芯片可以产生频率为488 Hz至2 MHz,占空比为50%的方波信号,且方波信号的频率随着输入电压的大小而线性变化;变化的频率信号f2控制开关电容模块的充放电速率使压电致动器两端的电荷量非线性变化,即可调节压电致动器的输出位移使其呈线性变化。

由于经典电荷泵驱动拟合曲线知压电致动器正反行程存在不同的非线性,所以需要对正反行程进行单独调节;通过逻辑比较模块检测电荷泵电路正反行程位移,产生方波输出信号;用逻辑比较模块的输出控制迟滞校正模块产生线性变化的电压信号。迟滞校正模块的系统框图如图4所示。

图4 迟滞校正模块系统框图Fig.4 Hysteresis correction module system block diagram

逻辑比较模块的输出传输给单片机;单片机对接收到的信号进行判断,当接收到高电平时产生斜率为k1的上升输出信号,当接收到低电平时产生斜率为k2的下降输出信号。由于正反行程的调节信号斜率不同,为了防止调节信号的漂移失真,所以每完成一次正反行程的校正之后,进行一次清零操作;将输出信号通过压频转换模块产生变化的频率信号控制开关电容模块的模拟开关S2,调节压电致动器输出位移的迟滞非线性。

测量经典电荷泵电路的输出位移,得到如式(3)所示的输出位移拟合曲线,由输出位移曲线确定该频率下的基准参数b和校正参数a。已知位移范围的频率为f1的输出位移曲线,所需基准参数为b1,校正参数为a1;则当需要频率为f2的输出时,所需基准参数为:

(5)

所需校正参数为:

(6)

通过一次参数校正即可得到其他任意频率的修正函数,校正控制简单方便。

4 实 验

4.1 实验装置

驱动时分别采用经典电荷泵方法和改进的电荷泵方法驱动压电致动器,经典电荷泵方法采用0～100 V的驱动信号进行驱动,改进的电荷泵方法同样采用0～100 V的驱动信号进行驱动。如图5所示,由单片机产生校正参数控制电荷泵的充放电速率;压电致动器的输出位移信号由电涡流位移传感器(安徽见行科技有限公司)进行检测,该型传感器测量范围为50 μm,分辨率为0.72 nm;采用24 bit数据采集卡(北京思迈科华技术有限公司,USB-6000)进行数据采集并传输上位机进行处理。

图5 改进的电荷泵驱动图Fig.5 Improved charge pump drive diagram

4.2 实验结果

给定压电致动器驱动信号频率为1 Hz时,实验结果如图6所示。

图6 改进的电荷泵迟滞改善效果Fig.6 Improved effect of hysteresis for improved charge pump

首先采用经典电荷泵驱动方法驱动压电致动器得到如图6(a)所示的拟合曲线,输出位移x(t)单位为μm,驱动时间t单位为s,通过经典电荷泵的拟合曲线得到基准参数b为1.6,压电致动器正行程校正参数a为0.45,压电致动器反行程校正参数a为-0.7。图6(a)为经典电荷泵方法驱动的压电致动器,其迟滞为2.83%,图6(b)为改进的电荷泵方法驱动的压电致动器,其迟滞为0.33%,较经典电荷泵驱动迟滞降低了88.34%。采用改进的电荷泵方法可以有效地降低压电致动器在经典电荷泵驱动下的迟滞非线性特性。

其余频率的实验结果如表3所示。其中,D1为采用经典电荷泵驱动时的迟滞;D2为采用改进的电荷泵驱动时的迟滞;F为迟滞降低百分比。

表3 改进的电荷泵不同频率迟滞降低百分比Tab.3 Improved charge pump hysteresis reduction by percentage of different frequencies (%)

给定驱动信号频率为1 Hz时,非线性实验结果如图7所示。由图7可知,采用改进的电荷泵驱动压电致动器可以有效降低压电致动器在经典电荷泵驱动下正反行程的非线性。非线性的实验结果详见表4 。

表4 改进的电荷泵非线性实验结果Tab.4 Non-linear experiment result of improved charge pump (%)

图7 改进的电荷泵正反行程的非线性改善效果Fig.7 Improvement effect of forward and backward travel nonlinear for improved charge pump

5 结 论

实验表明,改进的电荷泵驱动方法在低频下可以将迟滞降低至0.47%以下,能够较好地应用在低频且要求低迟滞高线性的应用场合。由于工作在开环情况下,可以避免采用高精度位移传感器所带来的高成本和系统复杂性,在光学隔振平台,扫描探针显微镜等微纳米测量领域,具有较大的应用价值。

受限于模拟开关频率大小以及电容充放电时间的影响,改进的电荷泵驱动方法输出位移曲线的频率有一定的限制。在压电致动器输出位移范围不变且电容充放电饱和的情况下,随着模拟开关S2切换频率的增大,压电致动器输出位移频率等倍增大。随着模拟开关S2切换频率的不断增大,开关电容充放电趋于不饱和,当电容充放电不饱和时,增大开关频率输出位移频率趋于稳定,此时可以通过增加基准电压的大小来提高输出位移的频率。

通过所述方法在改善经典电荷泵驱动迟滞非线性的同时,可以较大范围地提高所改进电荷泵驱动方法的应用场景,降低受限程度。