NTC热敏电阻温度计体温区内插方法研究
2023-12-06陈泽川陈伟昕孙建平王光耀李嘉豪邬潇洋
陈泽川, 潘 江, 陈伟昕, 李 婷, 孙建平,王光耀, 胡 靖, 李嘉豪, 邬潇洋
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018; 2.中国计量科学研究院,北京 100029; 3.中国石油大学(北京) 机械与储运工程学院,北京 102249)
1 引 言
在我国现行的温度量值传递体系中,标准水银体温计是检定人用体温计、兽用体温计以及各种电子体温计的标准器。随着《水俣公约》[1~3]的生效,标准水银体温计的使用受到限制,急需发展新的标准体温计。目前欧美等发达国家已基本实现以铂电阻或者负温度系数(negative temperature coefficient,NTC)热敏电阻为温度传感元件的电子体温计替代水银体温计,而我国在该方面的研究则鲜见报道。NTC热敏电阻温度计具有响应时间短、体积小、热惯性小、抗震特性良好等优点,特别是在窄温区的电阻稳定性与标准铂电阻温度计相当甚至更优,且价格更低廉[4~6]。因此,发展基于NTC热敏电阻的标准体温计,实现对现有标准水银体温计替代具有一定的可行性。
NTC热敏电阻非线性特性显著,对其有效的校准需要可靠的内插方法作为保障。国内外不乏关于NTC热敏电阻内插方程的研究。2015年德国国家物理技术研究院(PTB)开展热敏电阻应用于高精度温度测量研究,认为经典的Steinhart-Hart[7]方程不能满足精密温度测量对热敏电阻的要求;2014年由新西兰温度计量学家Rod White[8]提交的国际温度咨询委员文件建议NTC热敏电阻温度计计量校准至少需要4到5个校准点。然而这些研究主要针对的较宽温度范围,对于仅10 ℃范围的体温窄温区,相关研究依然匮乏。
参照现行JJG 881—1994《标准体温计检定规程》要求,测温范围35~45 ℃标准水银体温计以水三相点或冰点作为零位检定点,选取37、38、41、42 ℃ 4个点作为检定点,稳定性需优于30 mK,校准不确定度±0.02 ℃。当前规程的检定点及分布不适用于非线性显著的NTC热敏电阻温度计有效校准[9]。因此,挖掘适用于NTC热敏电阻温度计的内插方程和内插选点是非常重要的。本文拟开展NTC热敏电阻在体温范围(35~45 ℃)的内插方法探索,在对其稳定性考察的基础上,重点开展内插方程及内插选点分布研究,为发展基于NTC热敏电阻的标准体温计提供理论支撑。
2 装置及内插实验
实验选取高性能国产NTC热敏电阻作为研究对象,尺寸约2.5 mm×3 mm×8 mm,在水三相点温度对应名义阻值约为5 kΩ。在NTC热敏电阻温度计使用过程中,温度变化造成的自身机械开裂是引起热敏电阻不稳定性的主要因素。热敏电阻产生裂缝后,大气气体进入其内部,使得晶体的结构发生变化,从而导致温度的漂移[10]。长期稳定性是NTC热敏电阻温度计替代标准体温计成为标准器的必要条件。为了提高其稳定性,在其工作温度上下限进行热处理是必要手段。通过设置恒温槽温度在体温区上下限进行10次以上热循环,每经过2次热循环即利用国家温度基准镓熔点(29.764 6 ℃,不确定度0.58 mK,k=2)对NTC热敏电阻温度计进行稳定性考察。图1所示为20支NTC热敏电阻温度计在镓熔点1年内多次测量电阻最大差值的绝对值换算成的温度偏差。由图1可知,被测20支NTC热敏电阻温度计在镓熔点年稳定性优于4 mK,表明我国国产高精度NTC热敏电阻温度计具备替代标准水银体温计的潜力。
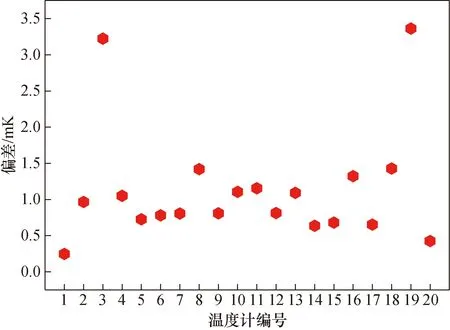
图1 NTC热敏电阻温度计1年稳定性考察结果Fig.1 Test results of the 1-year stability of NTC thermistor elements
实验装置主要组成部分为测温电桥、恒温水槽、氨热管、标准铂电阻温度计(SPRT)以及NTC热敏电阻温度计,如图2所示,其中下半部分为俯视图。为了减小恒温槽自身波动对内插实验产生的影响,提高恒温槽的稳定性和均匀性,将具有良好等温性的氨热管应用于恒温槽。经实验证明,热管的引入使内插实验恒温工作区的稳定性从 ±5 mK/30 min提高到±0.7 mK/30 min,均匀性提高到±0.5 mK/30 min,极大地减小了NTC热敏电阻的校准不确定度。在热管中插入一簇温度计阱,选用1支已校准的SPRT作为标准器,插入处于热管中心的阱中,被测NTC热敏电阻温度计插入其周围的阱中,保证标准温度计与被测NTC热敏电阻温度计尽量保持良好的温度一致性。分别利用Fluke1595高精度测温电桥和6015T高精度测温电桥同时测量SPRT与被测NTC热敏电阻温度计阻值,进一步得到被测NTC热敏电阻温度计阻温对应关系。
设置不同槽温,待恒温槽稳定后进行测试,在35~45 ℃温度范围每隔2 ℃进行1次测试,即35、37、39、41、43、45 ℃。
图3为其中1支NTC热敏电阻温度计电阻-温度特性曲线。由图可知,虽然NTC热敏电阻温度计具有显著的非线性特性,但是在体温区10 ℃温度范围内非线性特性并不明显。
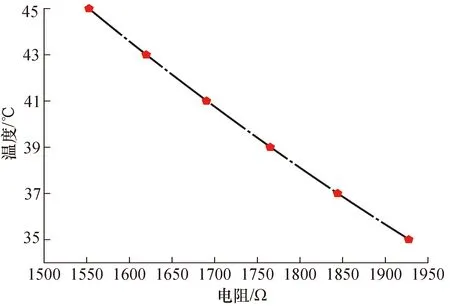
图3 NTC热敏电阻温度计校准结果图Fig.3 Calibration result of NTC thermistor thermometer
NTC热敏电阻温度计校准不确定度来源包括多次测量重复性、恒温槽均匀性、稳定性,参考温度计SPRT的校准不确定度,具体数值见表1所示。NTC热敏电阻温度计多次测量重复性由6015 T电桥读数的标准偏差获得,测量最大偏差优于0.8 mK,以均匀分布计算,不确定度分量为0.46 mK。SPRT在35~45 ℃的校准不确定度为0.80 mK(k=2),SPRT读数的不确定度由1595 A电桥读数的标准偏差获得。恒温槽均匀性、稳定性不确定度分量以实验测得数据按均匀分布计算。

表1 NTC热敏电阻温度计校准不确定度评估Tab.1 Calibration uncertainties of NTC thermistor thermometers mK
3 内插方程分析
目前国际上对于NTC热敏电阻温度计仍未有标准的内插方程。最基本的Basic方程广泛用于描述NTC热敏电阻的阻温特性[11],即:
(a) Basic方程
(1)
式中:RT为温度T(K)下热敏电阻的阻值;RT0为标称工作温度下热敏电阻的阻值;B为系数。
调研国内采用NTC热敏电阻进行测温的单位,大多还停留在基于Basic方程的阻温特性描述。然而,国外许多研究表明Basic方程并不是理想的NTC热敏电阻校准方程[12~14],采用Steinhart-Hart[15]方程和Hoge[16]系列方程可以获得更好的校准水平[17]。因此,本论文拟针对体温区特定温度范围,开展基于Steinhart-Hart方程和Hoge系列方程的内插方法研究,以获得适合的内插方程和校准点。
(b) Steinhart-Hart方程
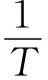
(2)
(c) Hoge-1方程
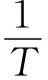
(3)
(d) Hoge-2方程
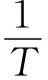
(4)
(e) Hoge-3方程
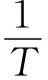
A3(lnRT)3+A4(lnRT)4
(5)
式中:T为热力学温度;A0,A1,A2,…,An为系数。对于Steinhart-Hart与Hoge-1两个方程至少需要3个校准点,Hoge-2方程至少需要4个校准点,Hoge-3方程至少需要5个校准点。
一般来说,NTC热敏电阻温度计校准时校准点越多,内插方程拟合阶数越高,校准精度越高。但是随着拟合阶数的增多,可能出现拟合曲线振荡的过度拟合现象,且校准点过多使得校准过程繁琐,不利于实际应用。因此在校准时结合实际应用需求来确定校准点数量是最好的方法之一。
本文根据20支热敏电阻温度计两轮校准实验数据,对这4个内插方程在体温区不同选点组合的情况下的内插特性进行研究,分析最优的选点组合。
NTC热敏电阻的内插方程在内插区域传播不确定度较小且平坦,在外推区域传播不确定度增长非常快。内插方程的阶数越高,该特性越明显[18]。为保证校准的准确性,拟合计算选取的温度点必须覆盖体温计的使用温度范围,因此35 ℃和45 ℃ 2个上下限温度点是必选的,其他温度点根据需要选择。对于至少需要3个校准点的Hoge-1、Steinhart-Hart的方程,除了2个必选点外再随机选取1个点,一共有4种内插选点组合。同理,对于至少4个校准点的Hoge-2方程,共有6种内插选点组合;对于至少5个校准点的Hoge-3方程,共有4种内插选点组合。
对于每支温度计,针对各方程不同选点组合,计算对应的内插系数;以未选点作为验证点,根据内插系数计算验证点的拟合温度,并与实际温度进行比较,计算所有验证点实际温度与拟合温度偏差的平均值,偏差最小的组合为该温度计的最优组合。统计20支温度计2次校准实验的最优组合情况,为尽量减小校准不确定度引入的统计误差,对于每支温度计2次校准数据,若1支温度计2次最优组合一致则说明该组合较好,计入统计,反之,则不计入统计。通过计算,图4所示为对应于3校准点Hoge-1、Steinhart-Hart内插方程的统计结果,图5所示为对应于4校准点Hoge-2内插方程的实验统计结果,图6为对应于5点Hoge-3内插方程的实验统计结果。
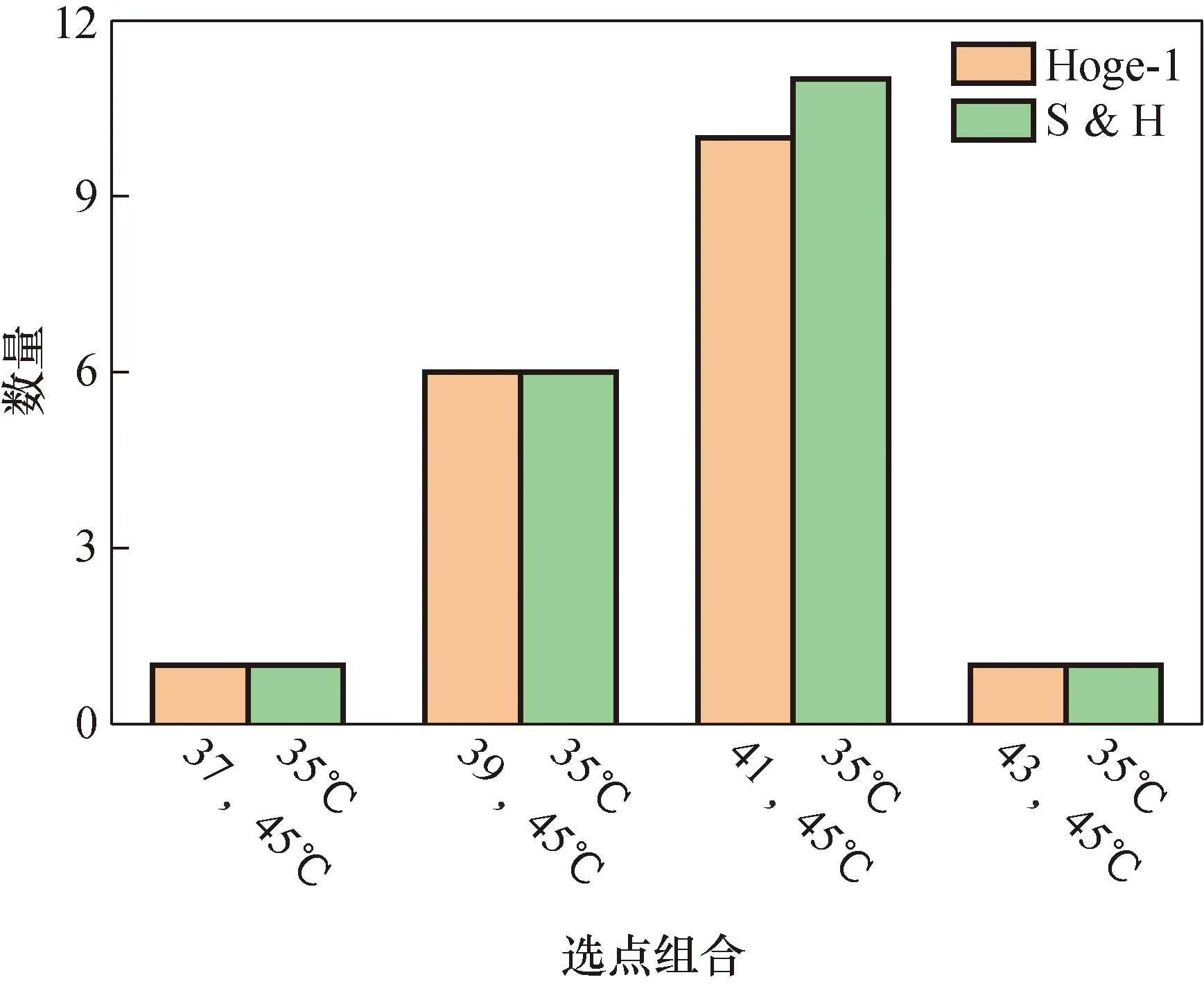
图4 3点内插不同选点统计结果Fig.4 Statistical results of point combinations corresponding to 3-points interpolation
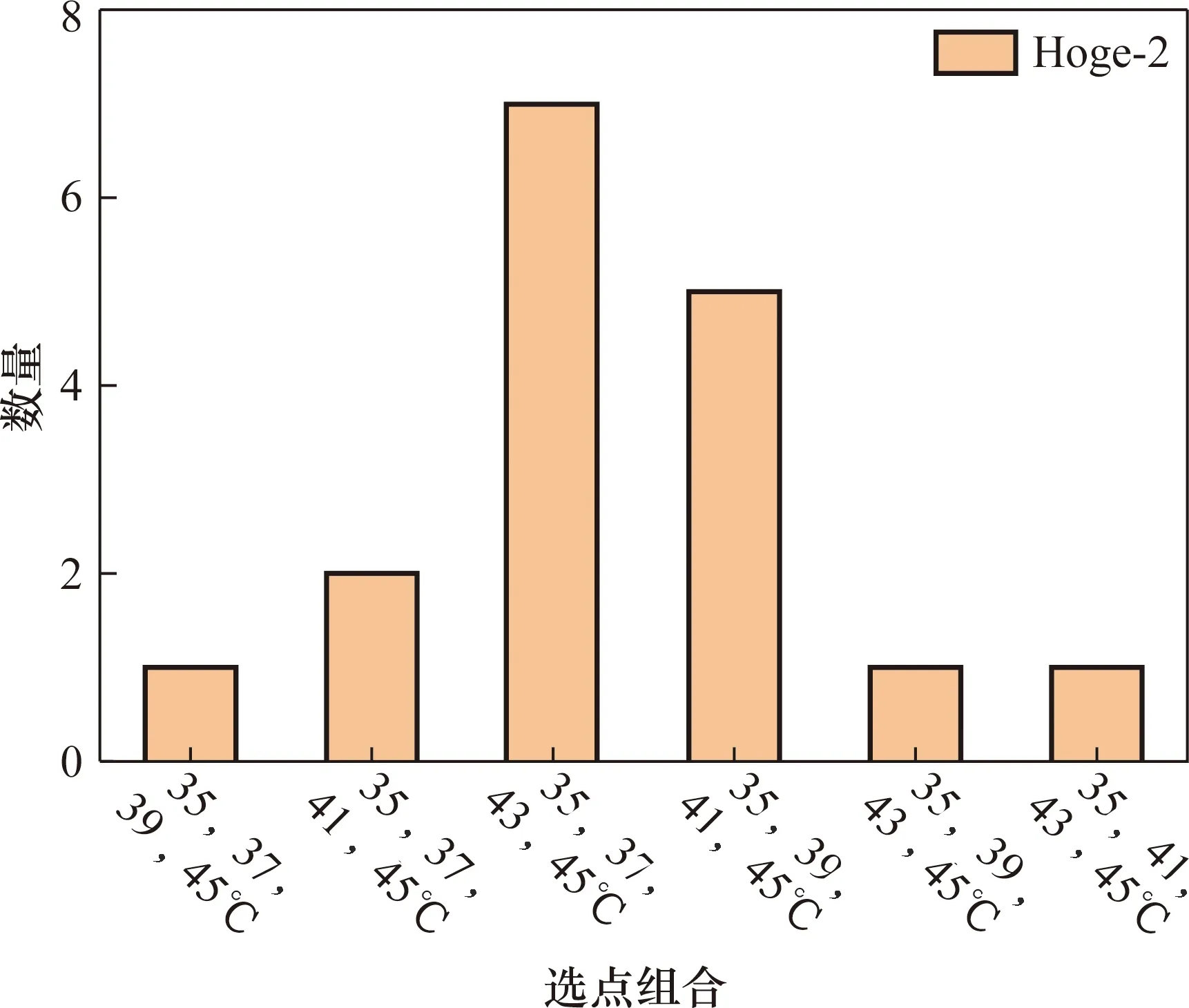
图5 4点内插不同选点统计结果Fig.5 Statistical results of point combinations corresponding to 4-points interpolation

图6 5点内插不同选点统计结果Fig.6 Statistical results of point combinations corresponding to 5-points interpolation
由图4~图6可知,对于3点内插方程,大多数温度计在(35、41、45 ℃)的内插组合时偏差最小。对于Hoge-2方程,(35、37、43、45 ℃)表现出更好的效果,略优于(35、39、41、45 ℃)组合并明显优于其余选点组合。对于Hoge-3方程,(35、37、39、43、45 ℃)的选点组合适用于大多数温度计,而(35、39、41、43、45 ℃)的选点组合表现出最差的效果,在20支温度计的两次实验结果中均无适用。
根据统计结果,可得如下结论:基于Hoge-1方程和Steinhart-Hart方程的3点内插最优的选点组合为35、41、45 ℃;对于基于Hoge-2方程的4点内插,最优的选点组合为35、37、43、45 ℃;对于基于Hoge-3方程的5点内插,最优的选点组合为35、37、39、43、45 ℃。图7所示为4个内插方程在对应的最优选点组合情况下的温度计阻温特性曲线,由图可见,相对于Hoge-2和Hoge-3方程的曲线,Steinhart-Hart和Hoge-1方程的曲线重合度更高。
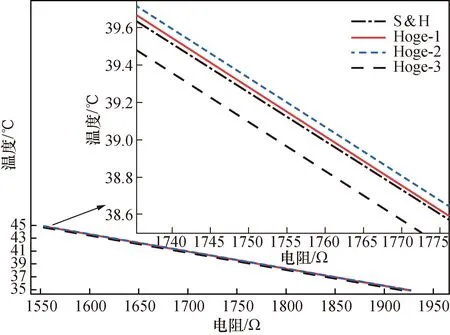
图7 一支温度计用4个不同的内插方程拟合的特性曲线Fig.7 Characteristic curve of a thermometer fitted with four different interpolation equations
为了进一步获得最适合于体温区的内插方程,计算4个内插方程在最优选点组合下的拟合残差以评估其性能[19]。拟合残差ΔT的定义为:
(6)
(7)
式中:|ΔTi|为ΔT的绝对值;n是校准点的数量。ΔTstd是拟合残差的实验标准差,定义为:
(8)

图8~图11所示为4个内插方程最佳选点情况下的验证点拟合残差ΔT的结果。计算对应的4个内插方程拟合残差的|ΔT|avg和ΔTstd,结果见表2所示。由表2可知,温度偏差随着内插点的增多而减少,且4个方程拟合残差都不超过3 mK。应用于3点校准的Hoge-1和Steinhart-Hart方程,其|ΔT|avg值和ΔTstd值相同,与Hoge-2、Hoge-3相比,偏差最大值增加也不足0.15 mK。在校准点相同的情况下,对于Hoge-1和Steinhart-Hart方程,前者的拟合残差结果略小于后者。此外,由于Steinhart-Hart方程忽略了二阶项,其校准性能可能会有一定下降,且Steinhart-Hart方程存在一些其他弊端[12],因此不推荐使用Steinhart-Hart方程。Hoge-1方程的最大拟合残差为1.2 mK左右,与Hoge-2方程相比,略增大0.1 mK左右,Hoge-3方程拟合残差均在0.6 mK以内。

表2 20支温度计的4个内插方程的评估参数Tab.2 Evaluation parameters of four interpolation equations for 20 thermometers mK
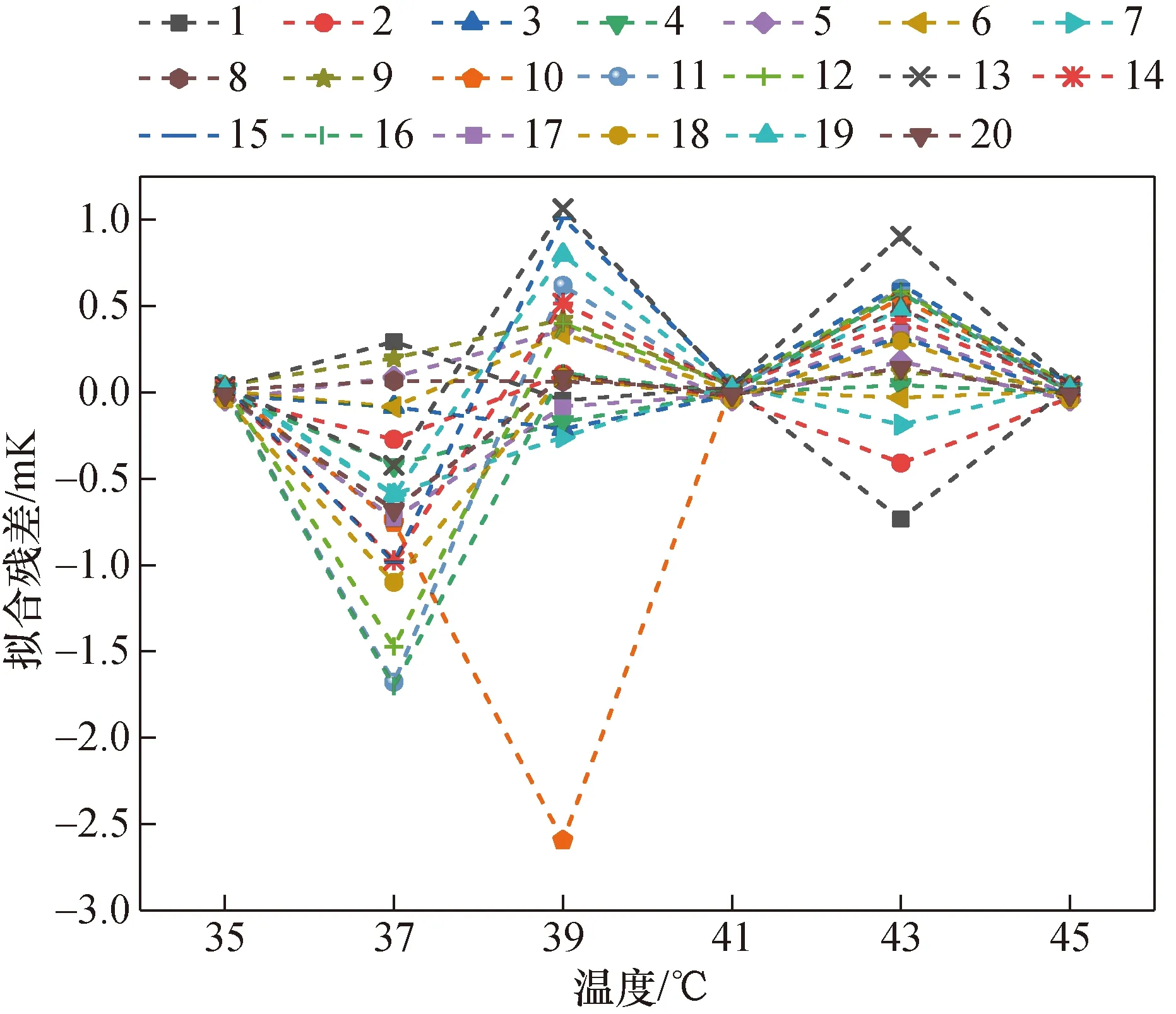
图8 Steinhart-Hart方程(35、41、45 ℃)拟合残差结果Fig.8 Fitting residual results of Steinhart-Hart equation with calibration point of (35, 41, 45 ℃)

图9 Hoge-1方程(35、41、45 ℃)拟合残差结果Fig.9 Fitting residual results of Hoge-1 equation with calibration point of (35, 41, 45 ℃)
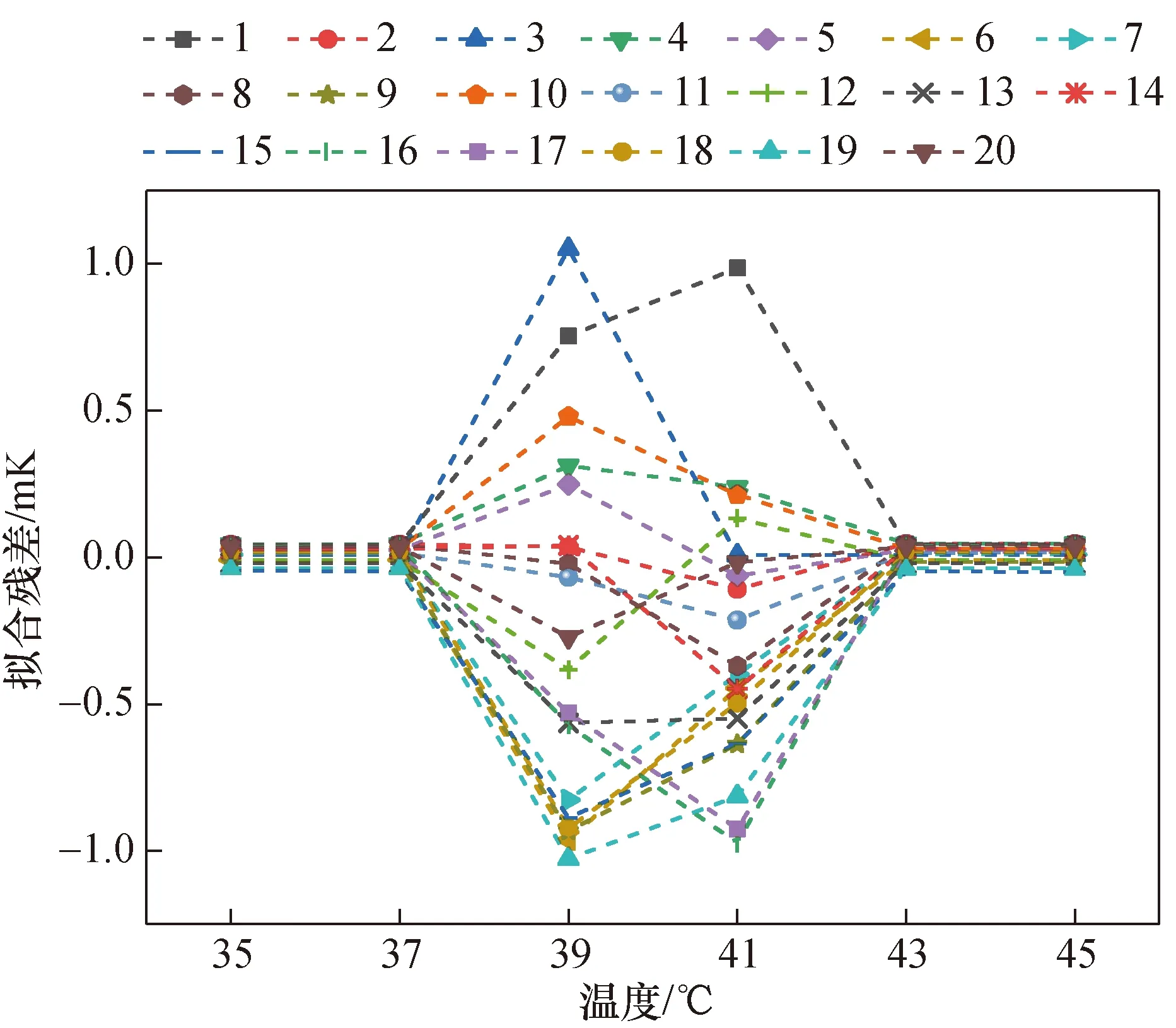
图10 Hoge-2方程(35、37、43、45 ℃)拟合残差结果Fig.10 Fitting residual results of Hoge-2 equation with calibration point of (35,37,43,45 ℃)

图11 Hoge-3方程(35、37、39、43、45 ℃)拟合残差结果Fig.11 Fitting residual results of Hoge-2 equation with calibration point of (35,37,39,43,45 ℃)
虽然随着校准点数量的增加,Hoge-2和Hoge-3方程的|ΔT|avg及ΔTstd减少,更加准确地描述了NTC热敏电阻的电阻-温度特性,但是需要更多的校准点。为了提高校准的效率,校准点数量应秉从“能少则少”的原则。对于体温区基于三点拟合的Hoge-1方程能完全满足体温区的实际校准需求,因此推荐使用Hoge-1方程作为体温区内校准NTC热敏电阻温度计使用的内插方程。
4 结 论
为应对《水俣公约》框架下替代标准水银体温计的迫在眉睫需求,基于国产高稳定性NTC热敏电阻温度计,开展了适用于体温区NTC热敏电阻温度计内插方法研究。
利用国家温度基准镓熔点装置对NTC热敏电阻温度计长期稳定性[20]进行考察,获得了年稳定性优于4 mK的高精度国产NTC热敏电阻温度计,具备替代潜力。针对体温区温度范围,开展NTC热敏电阻温度计内插方法研究,探索适用于体温区合适的内插方程及校准点组合。通过分析基于Steinhart-Hart方程和Hoge系列方程内插特性,结果表明:适用于Steinhart-Hart方程和Hoge-1方程的3点内插的最优校准点选取组合为:35、41、45 ℃;4点内插的最优校准点选取组合为:35、37、43、45 ℃;5点内插的最优校准点选取组合为:35、37、39、43、45 ℃。考虑到实际应用效率及方程特性,Hoge-1方程表现出更好的内插效果,最大拟合残差小于1.2 mK,推荐其作为体温区内校准NTC热敏电阻温度计的内插方程。
本项研究为发展基于NTC热敏电阻的标准体温计提供理论支撑,有助于实现对标准水银体温计的替代。
